Russ J.C. Image Analysis of Food Microstructure

Подождите немного. Документ загружается.

(c)

(d)

FIGURE 2.22 (continued)

2241_C02.fm Page 94 Thursday, April 28, 2005 10:23 AM

(e)

(f)

FIGURE 2.22 (continued)

2241_C02.fm Page 95 Thursday, April 28, 2005 10:23 AM

(g)

(h)

FIGURE 2.22 (continued)

2241_C02.fm Page 96 Thursday, April 28, 2005 10:23 AM

(a)

(b)

(c)

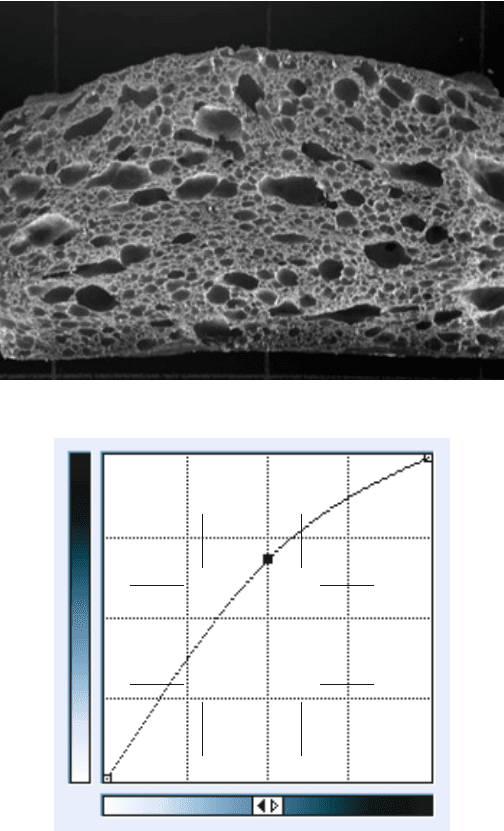
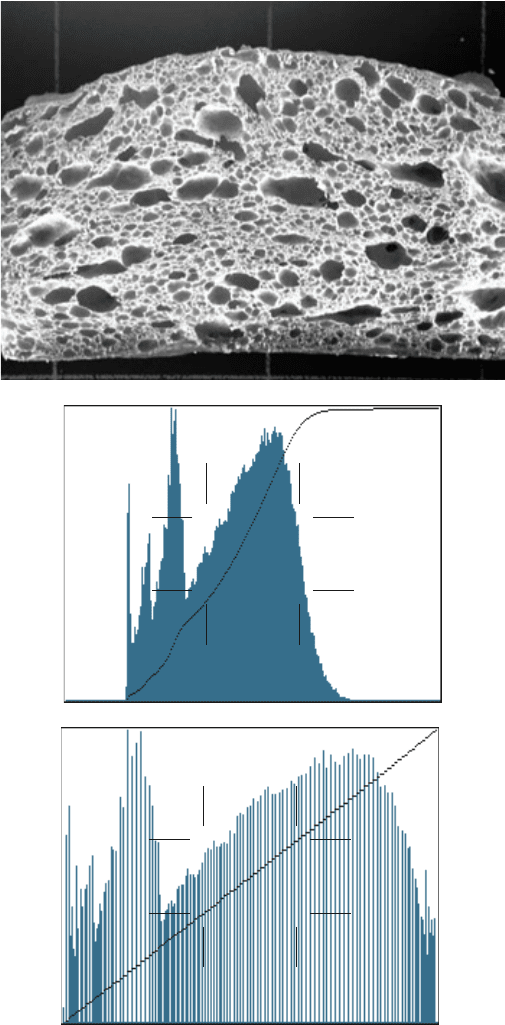
FIGURE 2.23 Histogram equalization: (a) result when applied to original image in Figure

2.20; (b) original histogram showing cumulative histogram used as transfer function; (c)

resulting histogram, showing linear cumulative histogram.

2241_C02.fm Page 97 Thursday, April 28, 2005 10:23 AM

REMOVING NOISE

Noise means many different things in different circumstances. Generally, it refers

to some part of the image signal that does not represent the actual subject but has

been introduced by the imaging system. In ﬁlm photography, the grains of halide

particles or the dye molecules may be described as “noise superimposed on the real

image.” So, too, may dust or scratches on the ﬁlm. There are rough equivalents to

these with digital photography, and some other problems as well.

A digital picture of a perfectly uniform and uniformly illuminated test card does

not consist of identical pixel values. The histogram of such an image typically shows

a peak with a generally Gaussian shape. The width of the peak is a measure of the

random variation or speckle in the pixels, which although much coarser than the

grain in ﬁlm, has the same underlying statistical characteristics. All of the processes

of generating charge in the detectors, transferring that charge out of the chip,

amplifying the analog voltage that results, and digitizing that voltage, are statistical

in nature. Some, such as the efﬁciency of each transistor, also vary because of the

ﬁnite tolerances of manufacture. For scanning microscopes, there are also both

statistical variations such as the production of X-rays or secondary electrons and

stability concerns such as the electron gun emission or creep in piezo drivers.

The statistical variations are sensitive to the magnitude of the signal. In the SEM,

increasing the beam current or slowing the scan rate down so that more electrons

are collected at each point, reduces the amount of the speckle as a percentage of the

value, and so reduces the width of the peak in the histogram as shown in Figure 2.24.

Instrumentation variations do not reduce in magnitude as the signal increases. Some,

such as transistor variations on the camera chip, do not vary with time, and are

described as “ﬁxed pattern noise.” The two types of noise are multiplicative noise

(proportional to signal) and additive noise (independent of signal), respectively.

Consider a test image consisting of greyscale steps (a similar image will be used

in Chapter 5 to calibrate measurements based on brightness). If an image contains

only additive noise, and if the detector is linear (output proportional to intensity)

the width of each peak corresponding to one of the grey scale steps would be the

same. If the image contains only multiplicative noise, the peak widths would be

proportional to the intensity value. Figure 2.24 illustrates both situations. This

changes if the ﬁnal output is logarithmic, in which case multiplicative noise produces

equal width peaks. In practice, most devices are subject to both types of noise and

the peak widths will vary with brightness but not in strict proportion. One of the

important characteristics of random noise is that the amount of noise in an image

varies from bright to dark areas, and some noise reduction schemes take this into

account.

Although the absolute amount of random noise may increase with signal, it

usually drops as a percentage of the signal. Collecting more signal by averaging

over time adds to the signal while the random variations may be either positive or

negative, and tend to cancel out. For purely multiplicative noise, the signal-to-noise

ratio increases as the square root of the averaging time. Of course, in many real

situations the strategy of temporal averaging (collecting more signal) to reduce noise

is not practical or even possible.

2241_C02.fm Page 98 Thursday, April 28, 2005 10:23 AM

(a)

(b)

(c)

(d)

FIGURE 2.24 Random noise superimposed on a series of brightness steps, and the image

histograms: (a, b) additive noise; (c, d) multiplicative noise.

2241_C02.fm Page 99 Thursday, April 28, 2005 10:23 AM

In most images, the size of features is much larger than the size of individual

pixels. That means that most of the pixels represent the same structure as their

neighbors, and should have the same value. So if temporal averaging to reduce noise

is impractical, spatial averaging should also offer a way to reduce noise. Figure 2.25

will be used to illustrate this procedure, and several others described below. A 7 pixel

wide circular neighborhood (actually an octagon, the closest approximation to a

circle possible on a square pixel grid) is moved across the image. At every position,

the values of the pixels in the neighborhood are averaged together and the result is

put into the pixel at the center of the circle (Figures 2.26b and 2.27b).

This is an example of a neighborhood operation. Unlike global operations, such

as the histogram stretching techniques described above, neighborhood operations

are a second major category of image processing operations. With this category of

procedures, two pixels that initially have the same value may end up with different

(a) (b)

FIGURE 2.25 SEM images at increasing magniﬁcation of chewing gum, showing the small

ﬂavor crystals embedded on the inside surface of the hollow chicle spheres. (Courtesy of Pia

Wahlberg, Danish Technological Institute)

2241_C02.fm Page 100 Thursday, April 28, 2005 10:23 AM

values if they have different neighborhoods. Neighborhood operations always use

the original pixel values from the image to calculate new values, not the newly calculated

values for other pixels in the neighborhood that have already been processed.

Notice in the image that the noise is reduced as expected, but the edges of

features have become blurred. The assumption that a pixel should be like its neigh-

bors is not met for pixels near feature edges. The averaging procedure blurs edges,

and can also shift their position or alter the shape which makes subsequent delin-

eation and measurement of features difﬁcult.

Instead of simple averaging in which all pixels in the neighborhood are added

equally, Gaussian smoothing uses weights for the pixels that vary with distance from

the center pixel. Plotting the weight values used in the kernel shows that they describe

a Gaussian or bell-shaped curve (Figure 2.28). The standard deviation of the Gaus-

sian controls the amount of smoothing and noise reduction. Ideally the weight values

should be real numbers and the neighborhood diameter should be about six times

(a) (b)

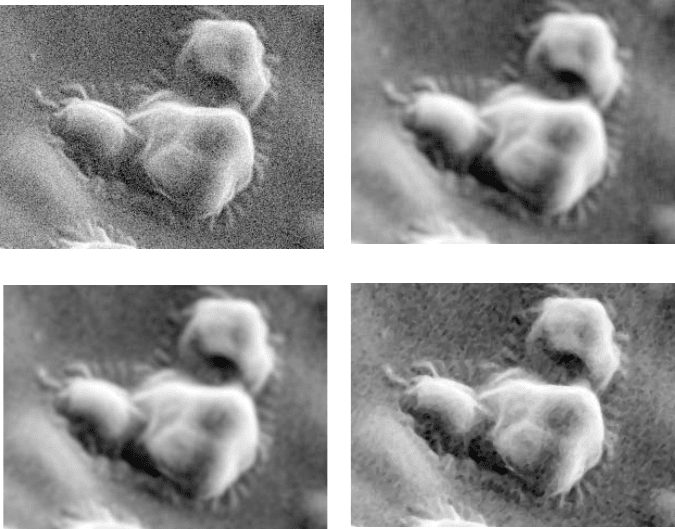
FIGURE 2.26 Enlarged fragments of the low magniﬁcation image from Figure 2.25 com-

paring the results of noise reduction methods: (a) original image; (b) averaging pixel values

in a 7 pixel wide circle; (c) Gaussian smooth with standard deviation of 2 pixel radius; (d)

median ﬁlter with a 7 pixel wide neighborhood.

2241_C02.fm Page 101 Thursday, April 28, 2005 10:23 AM

the standard deviation, but approximations with integer values and size truncation

are often used. Practically all image processing programs include Gaussian smooth-

ing. It can be implemented in a particularly efﬁcient way by separately smoothing

in the horizontal and vertical directions. Gaussian smoothing (Figures 2.26c and

2.27c) produces the least amount of edge blurring for a given amount of noise

reduction, but does not eliminate the problem.

This type of smoothing with a neighborhood kernel of weights is a low-pass

ﬁlter, because it tends to remove high frequencies (rapid local variations of bright-

ness) in the image while not affecting low frequencies (gradual overall variations in

brightness). This raises the important point that much image processing is actually

performed in frequency space with Fourier transforms, rather than in the pixel space

of the original values.

(a) (b)

FIGURE 2.27 Enlarged fragments of the high magniﬁcation image from Figure 2.25 com-

paring the results of noise reduction methods: (a) original image; (b) averaging pixel values

in a 7 pixel wide circle; (c) Gaussian smooth with standard deviation of 2 pixel radius; (d)

median ﬁlter with a 7 pixel wide neighborhood.

2241_C02.fm Page 102 Thursday, April 28, 2005 10:23 AM

(a)

(b)

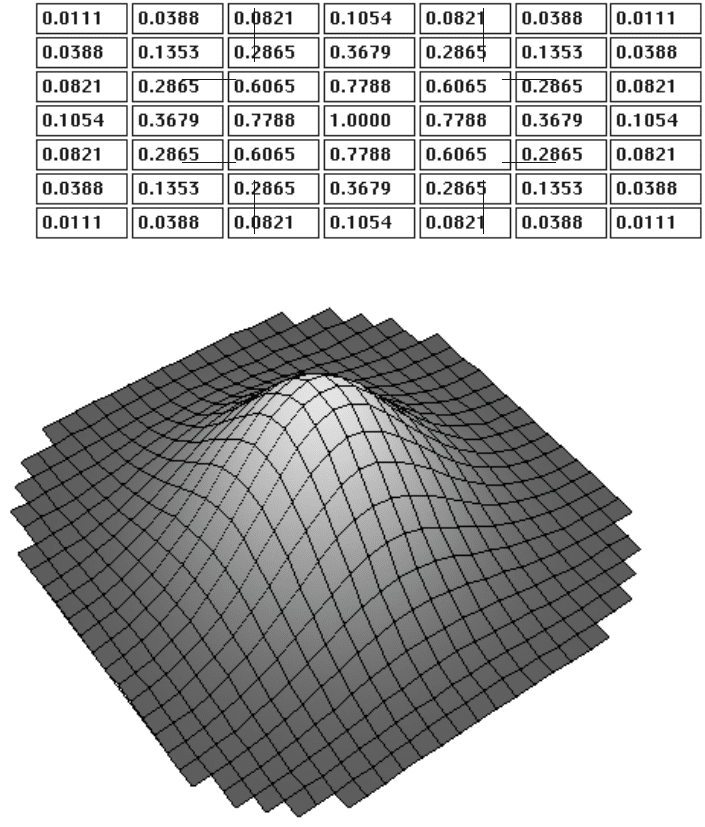
FIGURE 2.28 A Gaussian smoothing kernel consists of real number weights (or integer

approximations) that model the shape of a bell curve: (a) central portion of a Gaussian

smoothing kernel, weight values entered into a program dialog; (b) plot of the values for the

full kernel, which is 25 × 25 pixels in size.

2241_C02.fm Page 103 Thursday, April 28, 2005 10:23 AM