Руденко В.М. Математична статистика
Подождите немного. Документ загружается.

121
Ɂɚɤɨɧ ɜɟɥɢɤɢɯ ɱɢɫɟɥ ɫɬɜɟɪɞɠɭɽ, ɳɨ ɱɚɫɬɨɬɚ
n
m
ɩɨɞɿʀ Ⱥ ɛɭɞɟ ɫɤɿɥɶɤɢ ɡɚ-
ɜɝɨɞɧɨ ɛɥɢɡɶɤɨɸ ɞɨ ʀʀ ɣɦɨɜɿɪɧɨɫɬɿ
ɪ, ɹɤɳɨ ɱɢɫɥɨ ɜɢɩɪɨɛɭɜɚɧɶ n ɧɟɨɛɦɟɠɟɧɨ
ɡɪɨɫɬɚɽ. Ɇɨɠɧɚ ɜɡɹɬɢ ɫɤɿɥɶɤɢ ɡɚɜɝɨɞɧɨ ɦɚɥɟ ɱɢɫɥɨ
İ ɿ ɩɨɪɿɜɧɸɜɚɬɢ ɣɨɝɨ ɡ ɪɿɡ-
ɧɢɰɟɸ ɦɿɠ ɜɿɞɧɨɫɧɨɸ ɱɚɫɬɨɬɨɸ ɿ ɣɦɨɜɿɪɧɿɫɬɸ ɩɨɞɿʀ. Ƀɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ ɰɹ
ɪɿɡɧɢɰɹ ɩɟɪɟɜɢɳɢɬɶ ɱɢɫɥɨ
İ, ɩɪɚɝɧɭɬɢɦɟ ɞɨ ɧɭɥɹ ɩɪɢ ɩɪɚɝɧɟɧɧɿ ɱɢɫɥɚ ɜɢɩɪɨ-
ɛɭɜɚɧɶ
ɩ ɞɨ ɧɟɫɤɿɧɱɟɧɧɨɫɬɿ:
0o
°
¿
°
¾
½
°
¯
°
®
!
fo
H
n
p
n
m
P
.
Ɉɬɠɟ, ɱɚɫɬɨɬɚ ɩɨɞɿʀ ɿ ʀʀ ɿɦɨɜɿɪɧɿɫɬɶ ɧɟ ɫɩɿɜɩɚɞɚɸɬɶ, ɩɪɨɬɟ ɪɿɡɧɢɰɹ ɦɿɠ ɧɢ-
ɦɢ ɡɦɟɧɲɭɽɬɶɫɹ ɩɪɢ ɡɛɿɥɶɲɟɧɧɿ ɱɢɫɥɚ ɜɢɩɪɨɛɭɜɚɧɶ. ɐɟ ɡɧɚɱɢɬɶ, ɳɨ ɫɬɚɬɢɫ-
ɬɢɱɧɿ ɡɚɤɨɧɨɦɿɪɧɨɫɬɿ ɜɢɹɜɥɹɸɬɶɫɹ ɬɿɥɶɤɢ ɭ ɛɚɝɚɬɨɪɚɡɨɜɢɯ ɩɨɜɬɨɪɧɢɯ ɜɢɩɪɨ-
ɛɭɜɚɧɧɹɯ ɿ ɤɿɥɶɤɿɫɬɶ ɬɚɤɢɯ ɜɢɩɪɨɛɭɜɚɧɶ n ɩɨɜɢɧɧɚ ɛɭɬɢ ɡɧɚɱɧɨɸ.
Ɍɟɨɪɟɦɚ Ȼɟɪɧɭɥɥɿ
Ɍɟɨɪɟɦɚ Ȼɟɪɧɭɥɥɿ ɫɬɜɟɪɞɠɭɽ: ɹɤɳɨ m – ɤɿɥɶɤɿɫɬɶ ɩɨɞɿɣ Ⱥ ɜ n ɩɨɩɚɪɧɨ ɧɟ-
ɡɚɥɟɠɧɢɯ ɜɢɩɪɨɛɭɜɚɧɧɹɯ, ɚ
ɪ ɽ ɣɦɨɜɿɪɧɿɫɬɶ ɧɚɫɬɚɧɧɹ ɩɨɞɿʀ Ⱥ ɜ ɤɨɠɧɿɦ ɡ ɜɢ-
ɩɪɨɛɭɜɚɧɶ, ɬɨ ɩɪɢ ɛɭɞɶ-ɹɤɨɦɭ
İ>0 ɫɩɪɚɜɟɞɥɢɜɚ ɧɟɪɿɜɧɿɫɬɶ
2
)1(
H
H
n
pp
p
n
m
P
d
¿
¾
½
¯
®
t
. (3.40)
ɐɹ ɮɨɪɦɭɥɚ ɽ ɩɟɪɲɢɦ ɜ ɿɫɬɨɪɿʀ ɜɚɪɿɚɧɬɨɦ ɡɚɤɨɧɭ ɜɟɥɢɤɢɯ ɱɢɫɟɥ ɿ ɩɨ ɫɭɬɿ
ɜɜɚɠɚɽɬɶɫɹ ɩɨɱɚɬɤɨɦ ɬɟɨɪɿʀ ɣɦɨɜɿɪɧɨɫɬɟɣ ɹɤ ɝɚɥɭɡɿ ɦɚɬɟɦɚɬɢɱɧɨʀ ɧɚɭɤɢ. ȼɿɞ-
ɬɨɞɿ ɬɟɨɪɿʀ ɜɢɛɿɪɤɨɜɨɝɨ ɦɟɬɨɞɭ ɫɬɚɸɬɶ ɨɫɧɨɜɨɸ ɦɚɬɟɦɚɬɢɱɧɨʀ ɫɬɚɬɢɫɬɢɤɢ.
Ɍɟɨɪɟɦɚ Ȼɟɪɧɭɥɥɿ ɞɚɽ ɦɨɠɥɢɜɿɫɬɶ ɨɰɿɧɢɬɢ ɤɿɥɶɤɨɫɬɿ ɧɟɡɚɥɟɠɧɢɯ ɜɢɩɪɨɛɭ-
ɜɚɧɶ n ɩɪɢ ɩɟɜɧɢɯ ɭɦɨɜɚɯ ʀɯ
ɩɪɨɜɟɞɟɧɧɹ.
ɉɪɢɤɥɚɞ 3.16. Ƀɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ ɧɚɜɦɚɧɧɹ ɜɢɛɪɚɧɢɣ ɫɬɭɞɟɧɬ ɫɤɥɚɞɟ
ɡɚɥɿɤ, ɞɨɪɿɜɧɸɽ 90%. ɋɤɿɥɶɤɢ ɬɪɟɛɚ ɩɟɪɟɜɿɪɢɬɢ ɫɬɭɞɟɧɬɿɜ, ɳɨɛ ɡ ɿɦɨɜɿɪɧɿɫɬɸ
80% ɜɢɹɜɢɬɢ ɭɫɩɿɲɧɨ ɩɿɞɝɨɬɨɜɥɟɧɢɯ ɫɬɭɞɟɧɬɿɜ. ɉɨɯɢɛɤɚ ɩɪɢ ɰɶɨɦɭ ɧɟ ɩɨɜɢ-
ɧɧɚ ɩɟɪɟɜɢɳɭɜɚɬɢ 10%.
Ɋɿɲɟɧɧɹ:
122
ȼɢɡɧɚɱɢɦɨ ɜɿɞɩɨɜɿɞɧɿ ɞɨ ɬɟɨɪɟɦɢ Ȼɟɪɧɭɥɥɿ ɩɨɡɧɚɱɟɧɧɹ:
ɪ = 0,90 – ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ ɧɚɜɦɚɧɧɹ ɜɢɛɪɚɧɢɣ ɫɬɭɞɟɧɬ ɫɤɥɚɞɟ ɡɚɥɿɤ;
İ = 0,10 – ɩɨɯɢɛɤɚ ɩɪɨɰɟɞɭɪɢ ɩɟɪɟɜɿɪɤɢ ɫɬɭɞɟɧɬɿɜ;
¿
¾
½
¯
®
t 10,0p
n
m
P
=0,80 – ɣɦɨɜɿɪɧɿɫɬɶ ɜɢɹɜɥɟɧɧɹ ɩɿɞɝɨɬɨɜɥɟɧɢɯ ɫɬɭɞɟɧɬɿɜ.
Ɂɧɚɱɟɧɧɹ ɣɦɨɜɿɪɧɨɫɬɿ ɧɟ ɩɟɪɟɜɢɳɢɬɢ ɩɨɯɢɛɤɭ ɭ 10% ɩɪɨɰɟɞɭɪɢ ɩɟɪɟɜɿɪ-
ɤɢ ɫɬɭɞɟɧɬɿɜ ɫɤɥɚɞɚɽ
¿
¾
½
¯
®
10,0p
n
m
P
=1 – 0,80 = 0,20.
ɉɪɢ ɰɶɨɦɭ ɩɨɜɢɧɧɚ ɜɢɤɨɧɭɜɚɬɢɫɹ ɧɟɪɿɜɧɿɫɬɶ ɩɪɚɜɨʀ ɱɚɫɬɢɧɢ ɜɢɪɚɡɭ (3.40)
20,0
)1(
2
H
n
pp
.
Ɂɜɿɞɫɢ ɤɿɥɶɤɿɫɬɶ ɫɬɭɞɟɧɬɿɜ, ɹɤɢɯ ɬɪɟɛɚ ɩɟɪɟɜɿɪɢɬɢ, ɜɢɡɧɚɱɢɬɶɫɹ ɹɤ
.45
01,020,0
10,090,0
)10,0(20,0
)90,01(90,0
20,0
)1(
22
!
H
pp
n
ȼɿɞɩɨɜɿɞɶ: ɞɥɹ ɬɨɝɨ, ɳɨɛ ɡ ɿɦɨɜɿɪɧɿɫɬɸ 80% ɜɢɹɜɢɬɢ ɭɫɩɿɲɧɨ ɩɿɞɝɨɬɨɜɥɟ-
ɧɢɯ ɫɬɭɞɟɧɬɿɜ ɡ ɩɨɯɢɛɤɨɸ ɧɟ ɜɢɳɟ 10%, ɬɪɟɛɚ ɩɟɪɟɜɿɪɢɬɢ ɛɿɥɶɲɟ ɧɿɠ 45 ɨɫɿɛ.
Ɉɞɧɢɦ ɡ ɩɪɢɧɰɢɩɨɜɢɯ ɩɢɬɚɧɶ ɦɚɬɟɦɚɬɢɱɧɨʀ ɫɬɚɬɢɫɬɢɤɢ ɽ ɯɚɪɚɤɬɟɪ ɫɩɿɜ-
ɜɿɞɧɨɲɟɧɧɹ ɩɚɪɚɦɟɬɪɚ İ ɿ ɤɿɥɶɤɨɫɬɿ ɧɟɡɚɥɟɠɧɢɯ ɜɢɩɪɨɛɭɜɚɧɧɹɯ n. ȼɿɞɩɨɜɿɞɶ
ɧɚ ɰɟ ɩɢɬɚɧɧɹ ɬɚɤɨɠ ɞɚɽ ɡɚɤɨɧ ɜɟɥɢɤɢɯ ɱɢɫɟɥ.
ɉɪɢɤɥɚɞ 3.17. Ⱦɥɹ ɭɦɨɜ ɩɪɢɤɥɚɞɭ 3.16
ɨɰɿɧɢɬɢ ɫɩɿɜɜɿɞɧɨɲɟɧɧɹ ɤɿɥɶɤɨɫɬɿ
ɧɟɡɚɥɟɠɧɢɯ ɜɢɩɪɨɛɭɜɚɧɶ n ɿ ɩɚɪɚɦɟɬɪɚ İ ɞɥɹ ɬɪɶɨɯ ɡɧɚɱɟɧɶ İ (0,1; 0,05; 0,01).
Ɋɿɲɟɧɧɹ:
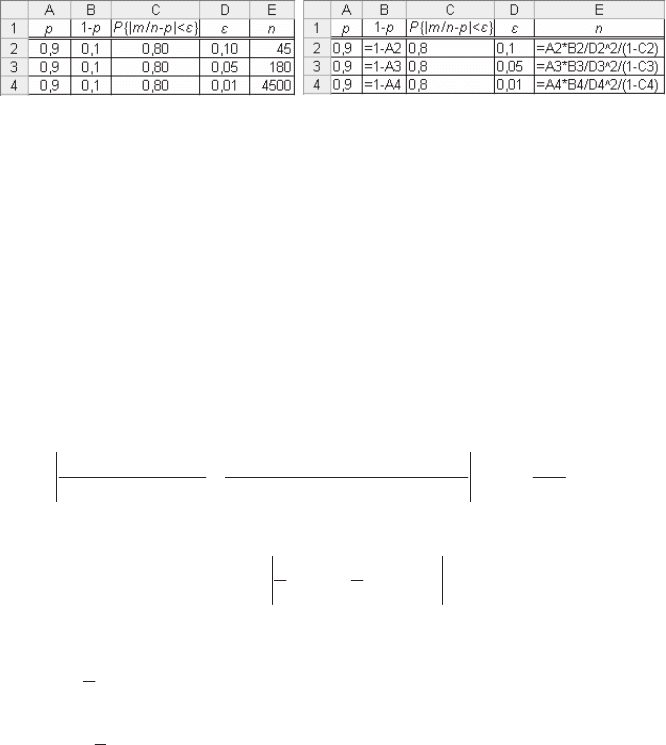
Ɋɟɡɭɥɶɬɚɬɢ ɿ ɮɨɪɦɭɥɢ ɪɨɡɪɚɯɭɧɤɭ n ɡɝɿɞɧɨ ɡ ɬɟɨɪɟɦɨɸ Ȼɟɪɧɭɥɥɿ (3.40) ɞɥɹ
ɪɿɡɧɢɯ ɡɧɚɱɟɧɶ İ ɩɪɟɞɫɬɚɜɥɟɧɨ ɜ ɬɚɛɥɢɱɧɿɣ ɮɨɪɦɿ ɧɚ ɪɢɫ. 3.29.
əɤ ɛɚɱɢɦɨ ɡ ɪɢɫ. 3.29 (ɞɢɜ. ɫɬɨɜɩɱɢɤɢ D ɿ E), ɩɪɢ ɡɦɟɧɲɟɧɧɿ ɩɚɪɚɦɟɬɪɚ İ
ɤɿɥɶɤɿɫɬɶ ɧɟɨɛɯɿɞɧɢɯ ɧɟɡɚɥɟɠɧɢɯ ɜɢɩɪɨɛɭɜɚɧɶ n ɡɪɨɫɬɚɽ ɩɪɨɩɨɪɰɿɣɧɨ İ
2
.
123
Ɋɢɫ. 3.29. Ɋɟɡɭɥɶɬɚɬɢ ɿ ɮɨɪɦɭɥɢ ɪɨɡɪɚɯɭɧɤɭ n ɞɥɹ ɪɿɡɧɢɯ İ
ȼɿɞɩɨɜɿɞɶ: ɱɢɦ ɠɨɪɫɬɤɿɲɿ ɭɦɨɜɢ İ ɳɨɞɨ ɡɦɟɧɲɟɧɧɹ ɪɿɡɧɢɰɿ ɦɿɠ ɟɦɩɿɪɢɱ-
ɧɨɸ ɱɚɫɬɨɬɨɸ ɩɨɞɿʀ ɬɚ ʀʀ ɬɟɨɪɟɬɢɱɧɨɸ ɣɦɨɜɿɪɧɿɫɬɸ, ɬɢɦ ɛɿɥɶɲɨʀ ɤɿɥɶɤɨɫɬɿ ɜɢ-
ɩɪɨɛɭɜɚɧɶ ɩɨɬɪɟɛɭɸɬɶ ɬɚɤɿ ɞɨɫɥɿɞɢ.
Ɍɟɨɪɟɦɚ ɑɟɛɢɲɟɜɚ
Ɍɟɨɪɟɦɚ ɑɟɛɢɲɟɜɚ ɫɜɿɞɱɢɬɶ: ɹɤɳɨ ɜɢɩɚɞɤɨɜɿ ɜɟɥɢɱɢɧɢ ɏ
1
, ɏ
2
, ..., ɏ
n
ɩɨɩɚ-
ɪɧɨ ɧɟɡɚɥɟɠɧɿ ɣ ɿɫɧɭɽ ɱɢɫɥɨ C ɬɚɤɟ, ɳɨ D[X
ɿ
] C ɞɥɹ ɜɫɿɯ ɿ = 1, 2, ..., n, ɬɨ ɞɥɹ
ɛɭɞɶ-ɹɤɨɝɨ İ>0 ɫɩɪɚɜɟɞɥɢɜɚ ɧɟɪɿɜɧɿɫɬɶ
2
2121
][][][
H
H
n
C
n
XMXMXM
n
XXX
P
nn
d
¿
¾
½
¯
®
t
!!
. (3.41)
ɇɟɪɿɜɧɿɫɬɶ (3.41) ɦɨɠɧɚ ɩɪɟɞɫɬɚɜɢɬɢ ɿɧɚɤɲɟ
.1][
11
lim
11
¿
¾
½
¯
®
¦¦
fo
H
n
i
i
n
i
i
n
XM
n
X
n
P (3.42)
Ɉɬɠɟ, ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ ɧɟɡɚɥɟɠɧɢɯ ɜɢɩɚɞɤɨɜɢɯ
ɜɟɥɢɱɢɧ
¦
n
i
i
X
n
1
1
ɜɿɞɪɿɡɧɹɽɬɶɫɹ ɜɿɞ ɫɟɪɟɞɧɶɨɝɨ ɚɪɢɮɦɟɬɢɱɧɨɝɨ ɦɚɬɟɦɚɬɢɱɧɢɯ
ɫɩɨɞɿɜɚɧɶ
¦
n
i
i
XM
n
1
][
1
ɦɟɧɲ ɧɿɠ ɧɚ İ, ɧɚɛɥɢɠɚɽɬɶɫɹ ɞɨ 1 ɩɪɢ ɡɪɨɫɬɚɧɧɿ ɱɢɫɥɚ
ɜɢɩɚɞɤɨɜɢɯ ɜɟɥɢɱɢɧ, ɞɥɹ ɛɭɞɶ-ɹɤɨɝɨ İ.
Ɍɟɨɪɟɦɚ ɑɟɛɢɲɟɜɚ ɽ ɪɨɡɜɢɬɤɨɦ ɿ ɭɡɚɝɚɥɶɧɟɧɧɹɦ ɬɟɨɪɟɦɢ Ȼɟɪɧɭɥɥɿ
Ⱦɥɹ ɩɪɚɤɬɢɱɧɢɯ ɰɿɥɟɣ ɧɚɣɱɚɫɬɿɲɟ ɜɢɤɨɪɢɫɬɨɜɭɽɬɶɫɹ ɬɚɤɢɣ ɜɚɪɿɚɧɬ ɜɢɩɪɨ-
ɛɭɜɚɧɶ, ɤɨɥɢ ɜɫɿ ɏ
ɿ
ɦɚɸɬɶ ɨɞɧɚɤɨɜɿ ɩɨɤɚɡɧɢɤɢ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ
M[ɏ
ɿ
]=Ɇ ɿ ɞɢɫɩɟɪɫɿʀ D[ɏ
ɿ
]=D. Ɍɨɞɿ ɭ ɹɤɨɫɬɿ ɨɰɿɧɤɢ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ
ɜɢɤɨɪɢɫɬɨɜɭɽɬɶɫɹ ɜɢɛɿɪɤɨɜɟ ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ
124
¦
n
i
i
n
X
nn
XXX
ɏ
1
21
1
!
,
ɡɜɿɞɤɢ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ ɿ ɞɢɫɩɟɪɫɿɹ ɫɟɪɟɞɧɶɨɝɨ ɜɢɡɧɚɱɚɬɶɫɹ ɹɤ
MXM
n
XM
n
X
n
MXM
n
i
i
n
i
i
n
i
i
»
¼
º
«
¬
ª
¦¦¦
][
1
][
11
][
111
,
D
n
D
nD
n
XD
n
X
n
DXD
n
i
i
n
i
i
»
¼
º
«
¬
ª
¦¦
2
1
2
1
1
][
11
][
.
Ɍɨɞɿ ɧɟɪɿɜɧɿɫɬɶ (3.41) ɦɚɬɢɦɟ ɜɢɝɥɹɞ
^`
2
][
][
H
H
XD
XMɏP dt (3.43)
ɚɛɨ
^`
2
H
H
n
D
MɏP
dt . (3.44)
Ɏɨɪɦɭɥɚ (3.44) ɨɡɧɚɱɚɽ, ɳɨ ɜɢɛɿɪɤɨɜɟ ɫɟɪɟɞɧɽ
ɏ
ɩɪɢ ɡɛɿɥɶɲɟɧɿ ɱɢɫɥɚ
ɜɢɩɪɨɛɭɜɚɧɶ (ɞɨɫɥɿɞɿɜ, ɫɩɨɫɬɟɪɟɠɟɧɶ, ɜɢɦɿɪɸɜɚɧɶ) ɹɤ ɡɚɜɝɨɞɧɨ ɛɥɢɡɶɤɨ ɡɚ
ɣɦɨɜɿɪɧɿɫɬɸ ɧɚɛɥɢɠɚɽɬɶɫɹ ɞɨ ɫɜɨɝɨ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ
][XM :
][XMɏ
p
o . (3.45)
Ɉɬɠɟ, ɜɢɪɚɡ (3.45) ɽ ɞɨɤɚɡɨɦ ɬɨɝɨ, ɳɨ ɜɢɛɿɪɤɨɜɟ ɫɟɪɟɞɧɽ
ɏ
ɽ ɫɩɪɨɦɨɠ-
ɧɨɸ ɨɰɿɧɤɨɸ ɫɜɨɝɨ ɚɧɚɥɨɝɚ ɡ ɝɟɧɟɪɚɥɶɧɨʀ ɫɭɤɭɩɧɨɫɬɿ. ɇɚ ɰɶɨɦɭ ɜɚɠɥɢɜɨɦɭ
ɜɢɫɧɨɜɤɭ ɩɨɛɭɞɨɜɚɧɨ ɫɬɚɬɢɫɬɢɱɧɟ ɨɰɿɧɸɜɚɧɧɹ (ɞɢɜ. ɪɨɡɞɿɥ 4).
ɉɪɢɤɥɚɞ 3.18. Ɉɰɿɧɢɬɢ ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ ɫɟɪɟɞɧɽ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ
ɜɿɞɯɢɥɢɬɶɫɹ ɜɿɞ ɫɜɨɝɨ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ ɧɚ ɡɧɚɱɟɧɧɹ ɧɟ ɛɿɥɶɲɟ ɧɿɠ
ɧɚ ɬɪɢ ɫɬɚɧɞɚɪɬɧɢɯ ɜɿɞɯɢɥɟɧɧɹ.
Ɋɿɲɟɧɧɹ:
ȼɢɡɧɚɱɢɦɨ ɜɿɞɩɨɜɿɞɧɿ ɞɨ ɬɟɨɪɟɦɢ ɑɟɛɢɲɟɜɚ ɩɨɡɧɚɱɟɧɧɹ:
ɏ
ɿ ][ ɏM – ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ ɜɟɥɢɱɢɧɢ ɏ ɿ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ
ɫɟɪɟɞɧɶɨɝɨ ɚɪɢɮɦɟɬɢɱɧɨɝɨ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɏ;
][ ɏSD
ɿ
][ɏD
– ɫɬɚɧɞɚɪɬɧɟ ɜɿɞɯɢɥɟɧɧɹ ɿ ɞɢɫɩɟɪɫɿɹ ɫɟɪɟɞɧɶɨɝɨ ɚɪɢɮɦɟɬɢ-
ɱɧɨɝɨ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɏ;
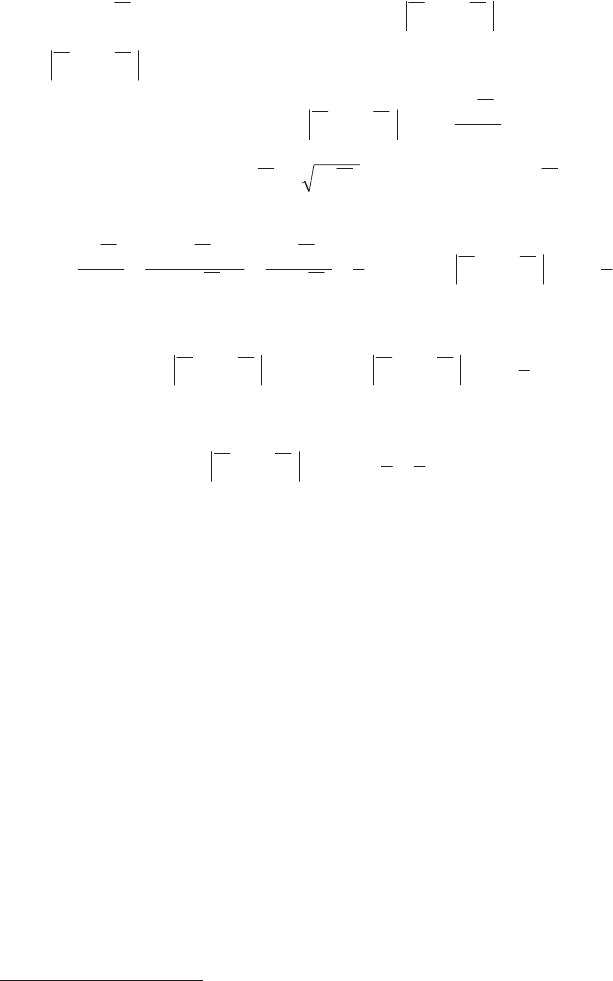
125
][3 ɏSD
H
– ɤɪɢɬɟɪɿɣ ɜɿɞɯɢɥɟɧɧɹ ɪɿɡɧɢɰɿ
][XMɏ
;
^
`
H
][XMɏP
– ɣɦɨɜɿɪɧɿɫɬɶ ɩɨɞɿʀ, ɹɤɭ ɬɪɟɛɚ ɨɰɿɧɢɬɢ ɡ ɭɦɨɜ ɡɚɞɚɱɿ.
Ɂɚ ɬɟɨɪɟɦɨɸ ɑɟɛɢɲɟɜɚ ɦɚɽɦɨ
^`
2
][
][
H
H
XD
XMɏP dt .
Ɂ ɭɪɚɯɭɜɚɧɧɹɦ ɜɢɪɚɡɭ
][][ ɏDɏSD
ɿ ɡɧɚɱɟɧɧɹ İ = ][3 ɏSD ɩɪɚɜɚ ɱɚɫ-
ɬɢɧɚ ɞɨɪɿɜɧɸɜɚɬɢɦɟ
9
1
][9
][
])[3(
][][
2
2
XD
XD
XSD
XDXD
H
, ɬɨɛɬɨ
^`
9
1
][ dt
H
XMɏP
Ɂ ɬɟɨɪɟɦɢ ɑɟɛɢɲɟɜɚ ɦɨɠɧɚ ɡɚɩɢɫɚɬɢ
^
`
H
][XMɏP
= 1 –
^`
9
1
][ dt
H
XMɏP .
Ɍɨɞɿ ɣɦɨɜɿɪɧɿɫɬɶ ɩɨɞɿʀ, ɹɤɭ ɬɪɟɛɚ ɨɰɿɧɢɬɢ, ɜɢɡɧɚɱɢɬɶɫɹ ɱɟɪɟɡ ɧɟɪɿɜɧɿɫɬɶ
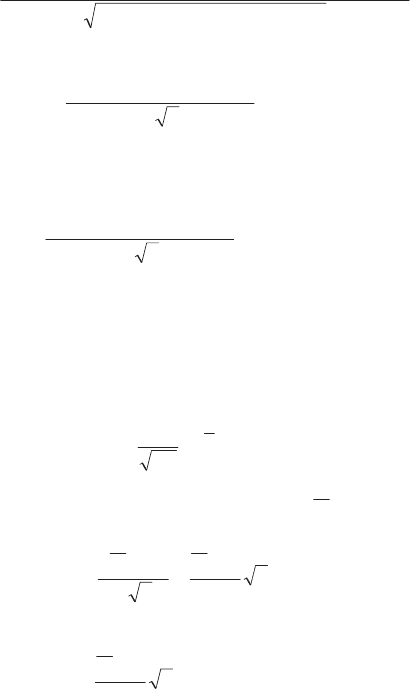
^`
89,0
9
8
9
1
1][ | !
H
XMɏP
17
.
ȼɿɞɩɨɜɿɞɶ: ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ ɫɟɪɟɞɧɽ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɜɿɞɯɢɥɢɬɶɫɹ
ɜɿɞ ɫɜɨɝɨ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ ɧɚ ɡɧɚɱɟɧɧɹ ɧɟ ɛɿɥɶɲɟ ɧɿɠ ɭ ɬɪɢ ɫɬɚɧɞɚ-
ɪɬɧɢɯ ɜɿɞɯɢɥɟɧɧɹ, ɫɤɥɚɞɚɽ ɩɪɢɛɥɢɡɧɨ 0,89 ɚɛɨ ɛɿɥɹ 89%.
Ɂ ɬɟɨɪɟɦ Ȼɟɪɧɭɥɥɿ ɿ ɑɟɛɢɲɟɜɚ ɹɤ ɡ ɤɨɧɤɪɟɬɧɢɯ ɮɨɪɦ ɡɚɤɨɧɭ ɜɟɥɢɤɢɯ ɱɢ-
ɫɟɥ ɜɢɩɥɢɜɚɽ ɬɨɣ ɮɚɤɬ, ɳɨ ɜɢɛɿɪɤɨɜɿ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɩɪɢ ɡɪɨɫɬɚɧɧɿ ɱɢɫɥɚ ɜɢ-
ɩɪɨɛɭɜɚɧɶ
ɧɚɛɥɢɠɚɸɬɶɫɹ ɞɨ ɬɟɨɪɟɬɢɱɧɢɯ, ɳɨ ɞɚɽ ɦɨɠɥɢɜɿɫɬɶ ɨɰɿɧɸɜɚɬɢ ɩɚ-
ɪɚɦɟɬɪɢ ɿɦɨɜɿɪɧɿɫɧɢɯ ɦɨɞɟɥɟɣ ɡɚ ɟɦɩɿɪɢɱɧɢɦɢ ɞɚɧɢɦɢ.
ɐɟɧɬɪɚɥɶɧɚ ɝɪɚɧɢɱɧɚ ɬɟɨɪɟɦɚ
Ɋɨɡɝɥɹɧɟɦɨ ɞɜɚ ɜɚɪɿɚɧɬɚ ɰɟɧɬɪɚɥɶɧɨʀ ɝɪɚɧɢɱɧɨʀ ɬɟɨɪɟɦɢ.
1. ɐɟɧɬɪɚɥɶɧɚ ɝɪɚɧɢɱɧɚ ɬɟɨɪɟɦɚ ɞɥɹ ɨɞɧɚɤɨɜɨ ɪɨɡɩɨɞɿɥɟɧɢɯ ɞɨɞɚɧɤɿɜ –
ɬɟɨɪɟɦɚ Ʌɿɧɞɟɛɟɪɝɚ-Ʌɟɜɿ.
Ⱦɥɹ ɧɟɡɚɥɟɠɧɢɯ ɨɞɧɚɤɨɜɨ ɪɨɡɩɨɞɿɥɟɧɢɯ ɜɢɩɚɞɤɨɜɢɯ ɜɟɥɢɱɢɧ X
1
, X
2
, ..., X
n
ɡ ɦɚɬɟɦɚɬɢɱɧɢɦɢ ɫɩɨɞɿɜɚɧɧɹɦɢ M[X
ɿ
] = ȝ ɿ ɞɢɫɩɟɪɫɿɹɦɢ D[X
ɿ
] = ı
2
(ɿ = 1, 2, ...,
17
dÍÌÑÆÚÊÑÆ ÒÙÑ±Æ ÑÒÉ ÌÆÑÍËÊÑÒá, ÑÆÓÔͱÏÆÉ, ÉÏÅ ÑÒÔÐÆÏßÑÒÒ ÔÒÌÓÒÉ-
Ͼ ÈÒÑÆ Õ±ÏÆÉÆ ÇÏÅ 0,997 (ÌÆ ÖƱ ÌÈÆÑÍÐ ÌƱÒÑ ÖÔßÒØ ÕÍÐ, ÉÍÈ. ÔÒÌÉÏ 3.4).
126
n) ɦɨɠɧɚ ɡɚɩɢɫɚɬɢ
Ɇ[X
1
+ X
2
+ … + X
n
] = Ɇ[X
1
] + Ɇ[X
2
] + ...+Ɇ[X
n
] = nȝ, (3.46)
D[X
1
+ X
2
+ … + X
n
] = D[X
1
] + D[X
2
] + ...+D[X
n
] = nı
2
. (3.47)
ȼɢɡɧɚɱɢɦɨ ɜɢɩɚɞɤɨɜɭ ɜɟɥɢɱɢɧɭ U
n
ɹɤ
][][][
][][][
21
2121
n
nn
n
XDXDXD
XMXMXMXXX
U
!
!!
.
Ɂ ɭɪɚɯɭɜɚɧɧɹ ɜɢɪɚɡɿɜ (3.46) ɿ (3.47) ɜɢɩɚɞɤɨɜɚ ɜɟɥɢɱɢɧɚ U
n
ɜɢɝɥɹɞɚɬɢɦɟ ɹɤ
n
nXXX
U
n
n
V
P
!
21
. (3.48)
Ⱦɥɹ ɜɟɥɢɱɢɧɢ U
n
ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ M[U
n
] = 0, ɞɢɫɩɟɪɫɿɹ D[U
n
] = 1.
Ɍɨɞɿ ɩɪɢ nĺ ɞɥɹ ɛɭɞɶ-ɹɤɨɝɨ ɱɢɫɥɚ ɯ ɿɫɧɭɽ ɝɪɚɧɢɰɹ
)(lim
21
xx
n
nXXX
P
n
n
)
¸
¹
·
¨
©
§
fo
V
P
!
, (3.49)
ɞɟ ĭ(ɯ) – ɮɭɧɤɰɿɹ ɫɬɚɧɞɚɪɬɧɨɝɨ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ
³
f
)
x
dttx )()(
M
, (3.50)
ɞɟ ij(t) – ɳɿɥɶɧɿɫɬɶ ɫɬɚɧɞɚɪɬɧɨɝɨ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ
2
2
2
1
)(
t
et
S
M
. (3.51)
əɤɳɨ ɜɪɚɯɨɜɭɜɚɬɢ, ɳɨ
XnXXXX
n
i
in
¦
1
21
! , ɬɨ ɡɦɿɧɧɭ U
n
ɦɨɠ-
ɧɚ ɡɚɩɢɫɚɬɢ ɹɤ
n
X
n
nXn
U
n
V
P
V
P
(3.52)
ɿ ɝɪɚɧɢɰɹ (3.48) ɩɪɢɣɦɚɽ ɛɿɥɶɲ ɡɧɚɣɨɦɭ ɮɨɪɦɚ ɡɚɩɢɫɭ
)1,0(lim Nxn
X
P
n
¸
¸
¹
·
¨
¨
©
§
fo
V
P
, (3.53)
ɞɟ N(0,1) - ɧɨɪɦɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ ɡ ɧɭɥɶɨɜɢɦ ɦɚɬɟɦɚɬɢɱɧɢɦ ɫɩɨɞɿɜɚɧɧɹɦ ɿ
ɫɬɚɧɞɚɪɬɧɢɦ ɜɿɞɯɢɥɟɧɧɹɦ, ɪɿɜɧɢɦ ɨɞɢɧɢɰɿ.
ɍ ɞɟɹɤɢɯ ɡɚɞɚɱɚɯ ɧɟ ɡɚɜɠɞɢ ɜɢɤɨɧɭɽɬɶɫɹ ɭɦɨɜɚ ɿɫɧɭɜɚɧɧɹ ɨɞɧɚɤɨɜɨ ɪɨɡ-
ɩɨɞɿɥɟɧɢɯ ɞɨɞɚɧɤɿɜ. ɋɭɬɧɿɫɬɶ ɰɢɯ ɭɦɨɜ ɩɨɥɹɝɚɽ ɜ ɬɨɦɭ, ɳɨ ɠɨɞɧɢɣ ɡ ɞɨɞɚɧɤɿɜ

127
ɧɟ ɩɨɜɢɧɧɢɣ ɛɭɬɢ ɞɨɦɿɧɭɸɱɢɦ, ɜɧɟɫɨɤ ɤɨɠɧɨɝɨ ɞɨɞɚɧɤɚ ɜ ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢ-
ɱɧɟ ɦɚɽ ɛɭɬɢ ɞɭɠɟ ɦɚɥɢɦ ɭ ɩɨɪɿɜɧɹɧɧɿ ɡ ɭɫɿɽɸ ɫɭɦɨɸ.
2. ɐɟɧɬɪɚɥɶɧɚ ɝɪɚɧɢɱɧɚ ɬɟɨɪɟɦɚ ɞɥɹ ɧɟɨɞɧɚɤɨɜɨ ɪɨɡɩɨɞɿɥɟɧɢɯ ɞɨɞɚɧɤɿɜ
– ɬɟɨɪɟɦɚ Ʌɹɩɭɧɨɜɚ.
Ⱦɥɹ ɧɟɡɚɥɟɠɧɢɯ ɧɟɨɞɧɚɤɨɜɨ ɪɨɡɩɨɞɿɥɟɧɢɯ ɜɢɩɚɞɤɨɜɢɯ ɜɟɥɢɱɢɧ X
1
, X
2
, ...,
X
n
ɡ ɦɚɬɟɦɚɬɢɱɧɢɦɢ ɫɩɨɞɿɜɚɧɧɹɦɢ M[X
ɿ
] = ȝ
ɿ
ɿ ɞɢɫɩɟɪɫɿɹɦɢ D[X
ɿ
] = ı
ɿ
2
0 (ɿ =
1, 2, ..., n) ɜɢɩɚɞɤɨɜɚ ɜɟɥɢɱɢɧɢ U
n
ɦɚɬɢɦɟ ɜɢɝɥɹɞ
»
¼
º
«
¬
ª
¦
n
i
i
nn
n
XD
XXX
U
1
2121
P
P
P
!!
(3.54)
Ɍɨɞɿ ɩɪɢ nĺ ɞɥɹ ɛɭɞɶ-ɹɤɨɝɨ ɱɢɫɥɚ
ɯ ɿɫɧɭɽ ɝɪɚɧɢɰɹ
)(lim
1
2121
xx
XD
XXX
P
n
i
i
nn
n
)
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
©
§
»
¼
º
«
¬
ª
¦
fo
PPP
!!
, (3.55)
ɞɟ
ĭ(ɯ) – ɮɭɧɤɰɿɹ ɫɬɚɧɞɚɪɬɧɨɝɨ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ.
ɍ ɪɚɡɿ ɧɟɡɚɥɟɠɧɢɯ ɨɞɧɚɤɨɜɨ ɪɨɡɩɨɞɿɥɟɧɢɯ ɜɢɩɚɞɤɨɜɢɯ ɞɨɞɚɧɤɿɜ ɦɚɽɦɨ
ȝ
1
= ȝ
2
= ... = ȝ
n
= ȝ ,
2
21
1
][
V
nXXXDXD
n
n
i
i
»
¼
º
«
¬
ª
¦
!
ɿ ɬɟɨɪɟɦɚ Ʌɹ-
ɩɭɧɨɜɚ ɩɟɪɟɯɨɞɢɬɶ ɭ ɬɟɨɪɟɦɭ Ʌɿɧɞɟɛɟɪɝɚ-Ʌɟɜɿ (3.49).
ɋɟɧɫ
ɰɟɧɬɪɚɥɶɧɨʀ ɝɪɚɧɢɱɧɨʀ ɬɟɨɪɟɦɢ ɬɚɤɢɣ: ɹɤɳɨ ɨɛɫɹɝ ɜɢɛɿɪɤɢ n ɽ «ɞɨ-
ɫɬɚɬɧɶɨ ɜɟɥɢɤɢɦ»,
ɬɨ ɧɟɡɚɥɟɠɧɨ ɜɿɞ ɮɨɪɦɢ ɪɨɡɩɨɞɿɥɭ ɩɚɪɚɦɟɬɪɚ ȝ ɝɟɧɟɪɚɥɶ-
ɧɨʀ ɫɭɤɭɩɧɨɫɬɿ
ɜɢɛɿɪɤɨɜɟ ɫɟɪɟɞɧɽ
X
ɦɚɽ ɪɨɡɩɨɞɿɥ, ɛɥɢɡɶɤɢɣ ɞɨ ɧɨɪɦɚɥɶɧɨɝɨ.
Ɉɬɠɟ, ɨɰɿɧɤɭ ɝɟɧɟɪɚɥɶɧɨɝɨ ɫɟɪɟɞɧɶɨɝɨ
ȝ ɡɚ ɣɨɝɨ ɜɢɛɿɪɤɨɜɢɦ ɡɧɚɱɟɧɧɹɦ
X
ɦɨɠɧɚ ɜɢɤɨɧɭɜɚɬɢ ɧɚ ɨɫɧɨɜɿ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ. ɋɯɟɦɚ ɞɨɫɥɿɞɠɟɧɧɹ ɦɨɠɟ
ɛɭɬɢ ɬɚɤɨɸ:
x ɜɢɛɢɪɚɽɦɨ ɜɢɩɚɞɤɨɜɢɦ ɦɟɬɨɞɨɦ n ɨɛ’ɽɤɬɿɜ ɏ
1
, ɏ
2
, …, ɏ
n
ɡ ɝɟɧɟɪɚɥɶɧɨʀ
ɫɭɤɭɩɧɨɫɬɿ (ɞɥɹ ɩɪɚɤɬɢɱɧɢɯ ɰɿɥɟɣ
n ɩɨɜɢɧɧɨ ɛɭɬɢ ɧɟ ɦɟɧɲɟ 30, ɬɨɛɬɨ n30);
x ɪɨɡɪɚɯɨɜɭɽɦɨ ɜɢɛɿɪɤɨɜɟ ɫɟɪɟɞɧɽ
¦
n
i
i
ɏ
n
X
1
1
;

128
x ɜɢɤɨɧɭɽɦɨ ɫɬɚɬɢɫɬɢɱɧɟ ɨɰɿɧɸɜɚɧɧɹ ɿ ɮɨɪɦɭɥɸɽɦɨ ɜɢɫɧɨɜɤɢ ɧɚ ɨɫɧɨɜɿ
ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ (ɞɢɜ., ɧɚɩɪɢɤɥɚɞ, ɪɨɡɞɿɥ 5.4).
ɐɟɧɬɪɚɥɶɧɚ ɝɪɚɧɢɱɧɚ ɬɟɨɪɟɦɚ – ɰɟ ɤɥɚɫ ɬɟɨɪɟɦ ɬɟɨɪɿʀ ɣɦɨɜɿɪɧɨɫɬɟɣ, ɳɨ
ɡɚɬɜɟɪɞɠɭɸɬɶ, ɳɨ ɫɭɦɚ ɜɟɥɢɤɨʀ ɤɿɥɶɤɨɫɬɿ ɧɟɡɚɥɟɠɧɢɯ (ɚɛɨ ɫɥɚɛɤɨ ɡɚɥɟɠɧɢɯ)
ɜɢɩɚɞɤɨɜɢɯ ɜɟɥɢɱɢɧ ɦɚɽ ɪɨɡɩɨɞɿɥ, ɛɥɢɡɶɤɢɣ ɞɨ ɧɨɪɦɚɥɶɧɨɝɨ.
Ⱦɭɠɟ ɜɚɠɥɢɜɨ ɬɟ, ɹɤ ɞɿɸɬɶ ɬɿ ɩɪɢɱɢɧɢ, ɡ ɹɤɢɯ ɫɤɥɚɞɚɽɬɶɫɹ ɫɭɤɭɩɧɢɣ ɪɟ-
ɡɭɥɶɬɚɬ ɜɢɦɿɪɸɜɚɧɶ ɚɛɨ ɫɩɨɫɬɟɪɟɠɟɧɶ: ɹɤɳɨ ɞɿɸɬɶ
ɚɞɞɢɬɢɜɧɨ (ɬɨɛɬɨ ɲɥɹɯɨɦ
ɞɨɞɚɜɚɧɧɹ), ɬɨ ɜɟɥɢɱɢɧɚ
ɏ ɦɚɽ ɩɪɢɛɥɢɡɧɨ ɧɨɪɦɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ; ɹɤɳɨ ɦɭɥɶ-
ɬɢɩɥɿɤɚɬɢɜɧɨ
(ɬɨɛɬɨ ɞɿʀ ɨɤɪɟɦɢɯ ɩɪɢɱɢɧ ɩɟɪɟɦɧɨɠɭɸɬɶɫɹ), ɬɨ ɪɨɡɩɨɞɿɥ ɏ ɽ
ɛɥɢɡɶɤɢɦ ɧɟ ɞɨ ɧɨɪɦɚɥɶɧɨɝɨ, ɚ ɞɨ ɬɚɤ ɡɜɚɧɨɝɨ ɥɨɝɚɪɢɮɦɿɱɧɨ ɧɨɪɦɚɥɶɧɨɝɨ,
ɬɨɛɬɨ ɧɟ
ɏ, ɚ lnX ɦɚɽ ɩɪɢɛɥɢɡɧɨ ɧɨɪɦɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ. əɤɳɨ ɠ ɧɟɦɚɽ ɩɿɞɫɬɚɜ
ɫɬɜɟɪɞɠɭɜɚɬɢ, ɳɨ ɞɿɽ ɨɞɢɧ ɿɡ ɰɢɯ ɞɜɨɯ ɦɟɯɚɧɿɡɦɿɜ ɮɨɪɦɭɜɚɧɧɹ ɩɿɞɫɭɦɤɨɜɨɝɨ
ɪɟɡɭɥɶɬɚɬɭ, ɬɨ ɩɪɨ ɪɨɡɩɨɞɿɥ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ
ɏ ɧɿɱɨɝɨ ɩɟɜɧɨɝɨ ɫɤɚɡɚɬɢ ɧɟ
ɦɨɠɧɚ.
Ɂɚɩɢɬɚɧɧɹ. Ɂɚɜɞɚɧɧɹ.
1. əɤɿ ȼɢ ɡɧɚɽɬɟ ɩɪɹɦɿ ɟɤɫɩɟɪɢɦɟɧɬɚɥɶɧɿ ɩɿɞɬɜɟɪɞɠɟɧɧɹ ɬɨɝɨ, ɳɨ ɱɚɫɬɨɬɚ
ɡɞɿɣɫɧɟɧɧɹ ɞɟɹɤɢɯ ɩɨɞɿɣ ɛɥɢɡɶɤɚ ɞɨ ɣɦɨɜɿɪɧɨɫɬɿ.
2.
ȼ ɱɨɦɭ ɽ ɩɪɨɹɜ ɞɿʀ ɬɚɤ ɡɜɚɧɨɝɨ ɡɚɤɨɧɭ ɜɟɥɢɤɢɯ ɱɢɫɟɥ?
3.
ɉɪɨɤɨɦɟɧɬɭɣɬɟ ɪɟɡɭɥɶɬɚɬɢ ɞɨɫɥɿɞɿɜ Ʉɟɬɥɟ.
4.
ɋɮɨɪɦɭɥɸɣɬɟ ɿ ɩɨɹɫɧɿɬɶ ɬɟɨɪɟɦɭ Ȼɟɪɧɭɥɥɿ.
5.
ɋɮɨɪɦɭɥɸɣɬɟ ɿ ɩɨɹɫɧɿɬɶ ɬɟɨɪɟɦɭ ɑɟɛɢɲɟɜɚ. ɑɢɦ ɜɨɧɚ ɜɿɞɪɿɡɧɹɽɬɶɫɹ ɜɿɞ
ɬɟɨɪɟɦɢ Ȼɟɪɧɭɥɥɿ?
6.
ɋɮɨɪɦɭɥɸɣɬɟ ɿ ɩɨɹɫɧɿɬɶ ɰɟɧɬɪɚɥɶɧɭ ɝɪɚɧɢɱɧɭ ɬɟɨɪɟɦɭ ɞɥɹ ɨɞɧɚɤɨɜɨ
ɪɨɡɩɨɞɿɥɟɧɢɯ ɞɨɞɚɧɤɿɜ (ɬɟɨɪɟɦɭ Ʌɿɧɞɟɛɟɪɝɚ-Ʌɟɜɿ).
7.
ɋɮɨɪɦɭɥɸɣɬɟ ɿ ɩɨɹɫɧɿɬɶ ɬɟɨɪɟɦɭ Ʌɹɩɭɧɨɜɚ.
8.
ɉɨɜɬɨɪɿɬɶ ɦɚɬɟɦɚɬɢɱɧɿ ɩɪɨɰɟɞɭɪɢ ɡɚɜɞɚɧɶ ɡɚ ɩɪɢɤɥɚɞɚɦɢ 3.16 – 3.18.

129
3.4. ɌȿɈɊȿɌɂɑɇȱ ɊɈɁɉɈȾȱɅɂ ȼɂɉȺȾɄɈȼɂɏ ȼȿɅɂɑɂɇ
Ɂɦɿɫɬ ɤɥɚɫɢɱɧɢɯ ɡɚɤɨɧɿɜ ɜɟɥɢɤɢɯ ɱɢɫɟɥ ɩɨɥɹɝɚɽ ɜ ɬɨɦɭ, ɳɨ ɜɢɛɿɪɤɨɜɟ ɫɟ-
ɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ ɧɟɡɚɥɟɠɧɢɯ ɨɞɧɚɤɨɜɨ ɪɨɡɩɨɞɿɥɟɧɢɯ ɜɢɩɚɞɤɨɜɢɯ ɜɟɥɢɱɢɧ
ɧɚɛɥɢɠɚɽɬɶɫɹ (ɫɯɨɞɢɬɶɫɹ ) ɞɨ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ ɰɢɯ ɜɟɥɢɱɢɧ. ȱɧɲɢ-
ɦɢ ɫɥɨɜɚɦɢ, ɜɢɛɿɪɤɨɜɿ ɫɟɪɟɞɧɿ ɫɯɨɞɹɬɶɫɹ ɞɨ ɬɟɨɪɟɬɢɱɧɨɝɨ ɫɟɪɟɞɧɶɨɝɨ.
Ȼɿɧɨɦɿɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ.
Ȼɿɥɶɲɿɫɬɶ ɡɚɜɞɚɧɶ ɬɟɨɪɿʀ ɣɦɨɜɿɪɧɨɫɬɟɣ ɩɪɢɩɭɫɤɚɸɬɶ ɜɿɞɨɦɢɦɢ ɿɡ ɫɚɦɨɝɨ
ɩɨɱɚɬɤɭ ɣɦɨɜɿɪɧɨɫɬɿ ɟɥɟɦɟɧɬɚɪɧɢɯ ɜɢɩɚɞɤɨɜɢɯ ɩɨɞɿɣ (ɧɚɩɪɢɤɥɚɞ, ɭɫɿ ɣɦɨɜɿɪ-
ɧɨɫɬɿ ɫɤɥɚɞɚɸɬɶ ɩɨ 0,5). ɋɩɢɪɚɸɱɢɫɶ ɧɚ ɡɧɚɧɧɹ ɰɢɯ ɣɦɨɜɿɪɧɨɫɬɟɣ, ɪɨɡɪɚɯɨ-
ɜɭɸɬɶ ɿɦɨɜɿɪɧɿɫɧɿ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɫɤɥɚɞɧɢɯ ɩɨɞɿɣ.
ɇɚɩɪɢɤɥɚɞ, ɤɨɠɧɢɣ ɿɫɩɢɬ ɨɞɧɨɝɨ ɫɬɭɞɟɧɬɚ (ɤɨɠɧɚ ɩɨɞɿɹ ȱ) ɫɤɥɚɞɚɽɬɶɫɹ ɡ
ɲɟɫɬɢ ɟɥɟɦɟɧɬɚɪɧɢɯ ɩɨɞɿɣ Ȧ
ɿ
(ɪɟɡɭɥɶɬɚɬɿɜ ɜɢɤɨɧɚɧɧɹ ɡɚɜɞɚɧɶ), ɬɨɛɬɨ ȱ={Ȧ
1
,
Ȧ
2
, …, Ȧ
n
}, ɞɟ n = 6. Ʉɨɠɧɚ ɟɥɟɦɟɧɬɚɪɧɚ ɩɨɞɿɹ Ȧ
ɿ
ɦɚɽ ɥɢɲɟ ɞɜɚ ɧɚɫɥɿɞɤɢ:
ɩɪɹɦɢɣ (ɛɚɠɚɧɢɣ) – «ɜɢɤɨɧɚɧɨ» (ɚɛɨ «1») ɿ ɩɪɨɬɢɥɟɠɧɢɣ (ɧɟɛɚɠɚɧɢɣ) – «ɧɟ
ɜɢɤɨɧɚɧɨ» (ɚɛɨ «0»). Ɋɨɡɝɥɹɧɟɦɨ ɜɚɪɿɚɧɬ ɬɚɤ ɡɜɚɧɨɝɨ «ɛɚɣɞɭɠɨɝɨ» ɫɬɭɞɟɧɬɚ,
ɹɤɢɣ ɧɚɦɚɝɚɽɬɶɫɹ ɫɤɥɚɫɬɢ ɿɫɩɢɬ, ɜɿɞɩɨɜɿɞɚɸɱɢ ɧɚɜɦɚɧɧɹ ɧɚ ɡɚɜɞɚɧɧɹ. Ɍɨɞɿ
ɦɨɠɧɚ ɩɪɢɣɧɹɬɢ, ɳɨ ɟɥɟɦɟɧɬɚɪɧɿ ɩɨɞɿʀ ɦɚɬɢɦɭɬɶ ɨɞɧɚɤɨɜɿ ɣɦɨɜɿɪɧɨɫɬɿ:
ɪ(1)=ɪ(0)=1/2=0,5. Ⱦɥɹ ɫɩɪɨɳɟɧɧɹ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɜɢɤɥɚɞɭ ɣɦɨɜɿɪɧɿɫɬɶ ɛɚɠɚ-
ɧɨʀ ɟɥɟɦɟɧɬɚɪɧɨʀ ɩɨɞɿʀ ɩɨɡɧɚɱɢɦɨ ɹɤ ɪ, ɬɨɛɬɨ ɪ(1) = ɪ. Ɍɨɞɿ:
ɪ(1) = ɪ = 0,5 ;
ɪ(0) = 1–ɪ(1) = (1–ɪ) = 1 – 0,5 = 0,5.
Ʉɿɥɶɤɿɫɬɶ ɛɚɠɚɧɢɯ ɟɥɟɦɟɧɬɚɪɧɢɯ ɩɨɞɿɣ (ɜɢɤɨɧɚɧɢɯ ɡɚɜɞɚɧɶ) m ɦɨɠɟ ɤɨ-
ɥɢɜɚɬɢɫɹ ɜɿɞ 0 (ɠɨɞɧɨɝɨ ɜɢɤɨɧɚɧɨɝɨ ɡɚɜɞɚɧɧɹ) ɞɨ 6 (ɭɫɿ ɡɚɜɞɚɧɧɹ ɿɫɩɢɬɭ ɜɢ-
ɤɨɧɚɧɨ). Ɋɨɡɪɚɯɭɽɦɨ ɣɦɨɜɿɪɧɨɫɬɿ ɬɨɝɨ, ɳɨ ɜ ɫɤɥɚɞɧɿɣ ɩɨɞɿʀ ȱ ɡ n ɟɥɟɦɟɧɬɚɪɧɢɯ
ɩɨɞɿɣ Ȧ
ɿ
ɦɨɠɧɚ ɨɬɪɢɦɚɬɢ m «ɛɚɠɚɧɢɯ» ɧɚɫɥɿɞɤɿɜ ɡ ɿɦɨɜɿɪɧɿɫɬɸ ɪ ɿ, ɡɪɨɡɭɦɿɥɨ,
n-m «ɧɟɛɚɠɚɧɢɯ» ɧɚɫɥɿɞɤɿɜ ɡ ɿɦɨɜɿɪɧɿɫɬɸ (1–p).
Ɂɚɝɚɥɶɧɚ ɣɦɨɜɿɪɧɿɫɬɶ ɨɞɧɿɽʀ ɬɚɤɨʀ ɫɤɥɚɞɧɨʀ ɩɨɞɿʀ ȱ ɞɨɪɿɜɧɸɽ ɞɨɛɭɬɤɭ ɣɦɨ-
ɜɿɪɧɨɫɬɟɣ ɧɟɡɚɥɟɠɧɢɯ ɟɥɟɦɟɧɬɚɪɧɢɯ ɩɨɞɿɣ ɿ ɨɛɱɢɫɥɸɽɬɶɫɹ ɹɤ:
130
mnm
pp
)1(
.
ɉɪɨɬɟ ɤɿɥɶɤɿɫɬɶ ɜɚɪɿɚɧɬɿɜ ɫɤɥɚɞɧɢɯ ɩɨɞɿɣ ȱ ɡ n ɟɥɟɦɟɧɬɿɜ ɩɨ m ɜɢɡɧɚɱɚɽɬɶ-
ɫɹ ɤɿɥɶɤɿɫɬɸ ɤɨɦɛɿɧɚɰɿɣ:
)!(!
!
mnm
n
C
m
n
.
Ɍɨɦɭ ɨɫɬɚɬɨɱɧɨ ɡɚɝɚɥɶɧɭ ɣɦɨɜɿɪɧɿɫɬɶ ɫɩɨɫɬɟɪɟɠɟɧɧɹ ɫɤɥɚɞɧɨʀ ɩɨɞɿʀ ȱ ɦɨ-
ɠɧɚ ɪɨɡɪɚɯɭɜɚɬɢ ɡɚ ɮɨɪɦɭɥɨɸ Ȼɟɪɧɭɥɥɿ:
mnmm
nn
ppCmP
)1()(
. (3.56)
ɐɹ ɮɨɪɦɭɥɚ ɜɢɡɧɚɱɚɽ ɬɟɨɪɟɬɢɱɧɢɣ ɪɨɡɩɨɞɿɥ ɣɦɨɜɿɪɧɨɫɬɟɣ ɫɤɥɚɞɧɢɯ ɩɨɞɿɣ
– ɬɚɤ ɡɜɚɧɢɣ
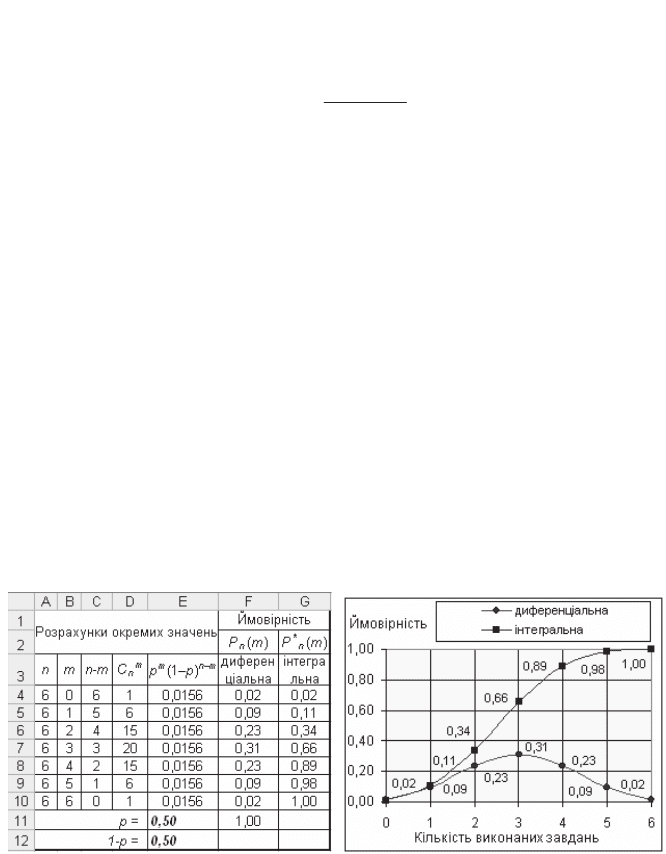
ɛɿɧɨɦɿɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ. ɇɚ ɪɢɫ. 3.30 ɧɚɜɟɞɟɧɨ ɣɨɝɨ ɪɨɡɪɚɯɭɧɤɢ
ɞɥɹ ɩɚɪɚɦɟɬɪɿɜ
n = 6, p = 0,5; ɧɚ ɪɢɫ. 3.31 – ɝɪɚɮɿɤɢ ɞɢɮɟɪɟɧɰɿɚɥɶɧɨʀ ɬɚ ɿɧɬɟɝ-
ɪɚɥɶɧɨʀ ɮɭɧɤɰɿɣ ɪɨɡɩɨɞɿɥɭ ɣɦɨɜɿɪɧɨɫɬɟɣ. ɇɟɨɛɯɿɞɧɨ ɦɚɬɢ ɧɚ ɭɜɚɡɿ, ɳɨ ɛɿɧɨ-
ɦɿɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ – ɰɟ ɪɨɡɩɨɞɿɥ ɞɢɫɤɪɟɬɧɨʀ ɡɦɿɧɧɨʀ.
Ⱦɥɹ ɪɨɡɪɚɯɭɧɤɿɜ ɛɿɧɨɦɿɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ ɡɪɭɱɧɨ ɜɢɤɨɪɢɫɬɨɜɭɜɚɬɢ ɮɭɧɤ-
ɰɿɸ =ȻɂɇɈɆɊȺɋɉ(
m; n; p; l), ɳɨ ɜɯɨɞɢɬɶ ɞɨ ɫɤɥɚɞɭ MS Excel. Ɏɭɧɤɰɿɹ ɩɨ-
ɜɟɪɬɚɽ ɞɢɫɤɪɟɬɧɿ ɡɧɚɱɟɧɧɹ ɪɨɡɩɨɞɿɥɭ, ɞɟ
m – ɤɿɥɶɤɿɫɬɶ ɭɫɩɿɯɿɜ; n – ɡɚɝɚɥɶɧɚ ɤɿ-
ɥɶɤɿɫɬɶ ɜɢɩɪɨɛɭɜɚɧɶ;
p – ɣɦɨɜɿɪɧɿɫɬɶ ɭɫɩɿɯɭ; l – ɩɚɪɚɦɟɬɪ, ɹɤɢɣ ɜɢɡɧɚɱɚɽ ɬɢɩ
ɪɨɡɩɨɞɿɥɭ (1 – ɿɧɬɟɝɪɚɥɶɧɚ ɮɭɧɤɰɿɹ, 0 – ɞɢɮɟɪɟɧɰɿɚɥɶɧɚ ɮɭɧɤɰɿɹ ɪɨɡɩɨɞɿɥɭ).
Ɋɢɫ. 3.30. Ɋɨɡɪɚɯɭɧɤɢ ɛɿɧɨɦɿɚɥɶɧɨɝɨ
ɪɨɡɩɨɞɿɥɭ (
n = 6; p = 0,50)
Ɋɢɫ. 3.31. Ƚɪɚɮɿɤɢ ɛɿɧɨɦɿɚɥɶɧɨɝɨ
ɪɨɡɩɨɞɿɥɭ (
n = 6; p = 0,50)
Ɋɨɡɩɨɞɿɥɢ ɦɨɠɧɚ ɪɨɡɪɚɯɭɜɚɬɢ ɿ ɞɥɹ ɿɧɲɢɯ ɚɩɪɿɨɪɧɢɯ ɣɦɨɜɿɪɧɨɫɬɟɣ ɛɚɠɚ-
ɧɢɯ ɟɥɟɦɟɧɬɚɪɧɢɯ ɩɨɞɿɣ. ɉɪɢɩɭɫɬɢɦɨ, ɳɨ ɞɥɹ «ɫɥɚɛɤɨɝɨ» ɫɬɭɞɟɧɬɚ ɣɦɨɜɿɪ-
ɧɿɫɬɶ
ɪ ɛɚɠɚɧɨʀ ɩɨɞɿʀ ɫɤɥɚɞɚɽ, ɧɚɩɪɢɤɥɚɞ, 30% ɚɛɨ 0,3. ɇɚ ɪɢɫ. 3.32 ɧɚɜɟɞɟɧɨ
