Руденко В.М. Математична статистика
Подождите немного. Документ загружается.

101
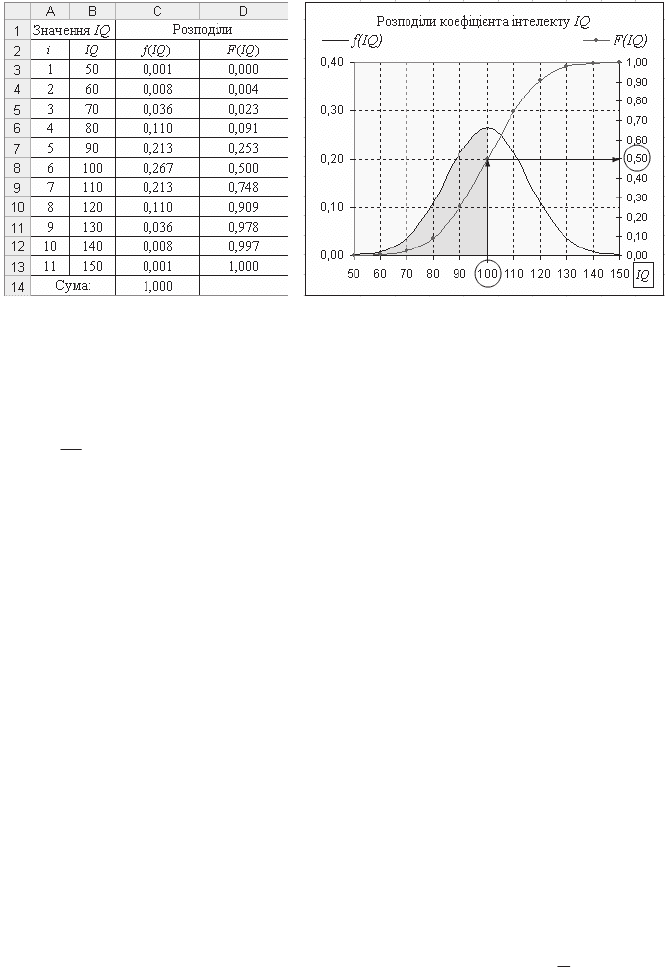
Ɋɢɫ. 3.12. Ɍɚɛɥɢɰɹ ɪɨɡɩɨɞɿɥɭ IQ Ɋɢɫ. 3.13. Ƚɪɚɮɿɤɢ ɪɨɡɩɨɞɿɥɭ IQ
ɋɥɿɞ ɡɜɟɪɧɭɬɢ ɭɜɚɝɭ ɧɚ ɬɟ, ɳɨ ɣɦɨɜɿɪɧɿɫɬɶ P(IQ 100) = 0,50. ȱɧɚɤɲɟ ɤɚ-
ɠɭɱɢ, ɣɦɨɜɿɪɧɿɫɬɶ ɨɬɪɢɦɚɬɢ ɡɧɚɱɟɧɧɹ IQ ɧɚ ɪɿɜɧɿ ɧɟ ɛɿɥɶɲɟ ɫɟɪɟɞɧɶɨɝɨ ɡɧɚ-
ɱɟɧɧɹ
IQ
=100 ɫɤɥɚɞɚɽ 50%. ɇɚ ɪɢɫ. 3.13 ɰɟ ɜɿɞɩɨɜɿɞɚɽ ɡɚɮɚɪɛɨɜɚɧɿɣ ɩɥɨɳɿ,
ɹɤɚ ɫɤɥɚɞɚɽ 50% ɜɿɞ ɡɚɝɚɥɶɧɨʀ. Ⱥɧɚɥɿɬɢɱɧɨ ɰɟ ɦɨɠɧɚ ɡɚɩɢɫɚɬɢ ɬɚɤ:
³
f
d
100
)()100( dxxfxF = 0,50.
Ɋɨɡɝɥɹɧɟɦɨ ɩɭɧɤɬɢ ɡɚɜɞɚɧɧɹ ɳɨɞɨ ɜɢɡɧɚɱɟɧɧɹ ɣɦɨɜɿɪɧɨɫɬɿ ɨɬɪɢɦɚɧɧɹ
ɤɨɧɤɪɟɬɧɢɯ ɡɧɚɱɟɧɶ ɤɨɟɮɿɰɿɽɧɬɚ ɿɧɬɟɥɟɤɬɭ IQ.
ɚ) ȼɢɡɧɚɱɢɬɢ ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ IQ
ɩɪɢɣɦɚɬɢɦɟ ɡɧɚɱɟɧɧɹ ɧɟ ɛɿɥɶɲɟ 80,
ɬɨɛɬɨ Ɋ(IQ
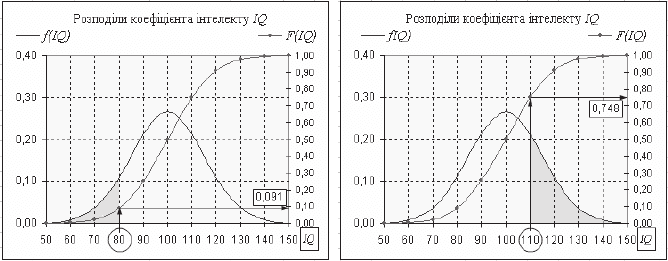
80). ɐɿɣ ɫɢɬɭɚɰɿʀ ɜɿɞɩɨɜɿɞɚɽ ɡɚɮɚɪɛɨɜɚɧɚ ɩɥɨɳɚ ɪɢɫ. 3.14, ɞɥɹ
ɹɤɨʀ F(80) § 0,091 (ɡɧɚɱɟɧɧɹ 0,091 ɦɨɠɧɚ ɨɬɪɢɦɚɬɢ ɡ ɬɚɛɥ. ɪɢɫ. 3.12). Ⱥɧɚɥɿ-
ɬɢɱɧɢɣ ɡɚɩɢɫ ɦɚɽ ɜɢɝɥɹɞ:
³
f
d
80
)()80( dxxfxF § 0,091.
Ɉɬɠɟ, ɣɦɨɜɿɪɧɿɫɬɶ Ɋ(IQ
80) § 0,091 = 9,1%.
ɛ) ȼɢɡɧɚɱɢɬɢ ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ ɡɧɚɱɟɧɧɹ IQ
ɧɟ ɦɟɧɲɟ 110, ɬɨɛɬɨ
Ɋ(IQ>110). Ɂɚɮɚɪɛɨɜɚɧɚ ɩɥɨɳɚ ɪɢɫ. 3.15 ɜɿɞɩɨɜɿɞɚɽ ɫɢɬɭɚɰɿʀ, ɤɨɥɢ ɬɪɟɛɚ ɨɬɪɢ-
ɦɚɬɢ ɩɨɞɿɸ Ⱥ{IQ>110}, ɹɤɚ ɽ ɞɨɩɨɜɧɟɧɧɹɦ ɩɪɨɬɢɥɟɠɧɨʀ ɩɨɞɿʀ
}110{ dIQȺ .
ɋɭɦɚ ɣɦɨɜɿɪɧɨɫɬɟɣ ɩɪɨɬɢɥɟɠɧɢɯ ɩɨɞɿɣ ɞɨɪɿɜɧɸɽ ɨɞɢɧɢɰɿ. Ɂɜɿɞɫɢ ɣɦɨɜɿɪɧɿɫɬɶ
102
ɛɚɠɚɧɨʀ ɩɨɞɿʀ Ɋ(IQ>110) = 1 –
)110( dI
Q
Ɋ
ɿ ɚɧɚɥɿɬɢɱɧɢɣ ɡɚɩɢɫ ɞɥɹ ɜɢɡɧɚɱɟɧɧɹ
ɜɿɞɩɨɜɿɞɧɨʀ ɣɦɨɜɿɪɧɨɫɬɿ ɡɚ ɞɨɩɨɦɨɝɨɸ ɮɭɧɤɰɿɣ ɪɨɡɩɨɞɿɥɭ ɬɚɤɢɣ:
³
f
d !
110
)(1)110(1)110( dxxfxFxF
= 1 – 0,748 § 0,252.
Ɂɧɚɱɟɧɧɹ F(110) = 0,748 ɦɨɠɧɚ ɨɬɪɢɦɚɬɢ ɡ ɬɚɛɥ. ɪɢɫ. 3.12.
Ɉɬɠɟ, ɣɦɨɜɿɪɧɿɫɬɶ Ɋ(IQ>110) § 25,2%.
Ɋɢɫ. 3.14. Ƀɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ IQ ɧɟ
ɩɟɪɟɜɢɳɭɽ 80, ɚɛɨ Ɋ(IQ
80) § 9,1%
Ɋɢɫ. 3.15. Ƀɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ IQ
ɧɟ
ɦɟɧɲɟ 110, ɬɨɛɬɨ Ɋ(IQ>110) § 25,2%
ɜ) ȼɢɡɧɚɱɢɬɢ ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ IQ
ɩɪɢɣɦɚɬɢɦɟ ɡɧɚɱɟɧɧɹ ɧɟ ɦɟɧɲɟ 70,
ɚɥɟ ɧɟ ɛɿɥɶɲɟ 90, ɬɨɛɬɨ Ɋ(70 IQ
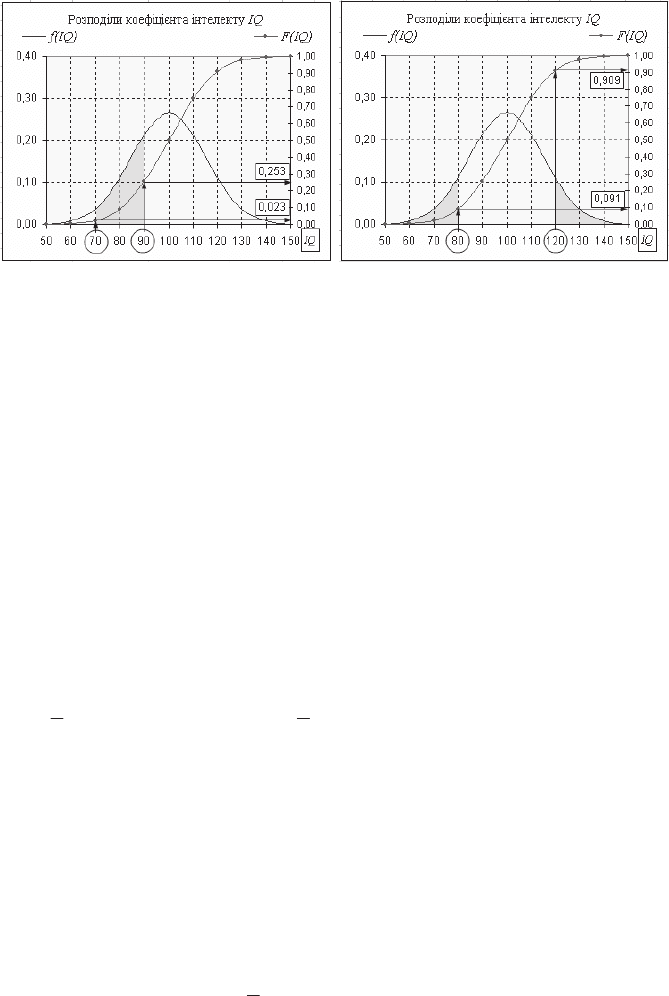
90). Ɂɚɮɚɪɛɨɜɚɧɚ ɩɥɨɳɚ ɪɢɫ. 3.16 ɜɿɞɩɨɜɿ-
ɞɚɽ ɫɢɬɭɚɰɿʀ, ɤɨɥɢ ɡ ɩɨɞɿʀ Ⱥ
1
{IQ
90} ɬɪɟɛɚ ɜɢɥɭɱɢɬɢ ɟɥɟɦɟɧɬɢ ɩɨɞɿʀ Ⱥ
2
{IQ
70}. Ɍɨɞɿ ɣɦɨɜɿɪɧɿɫɬɶ Ɋ(Ⱥ) ɛɚɠɚɧɨʀ ɩɨɞɿʀ Ⱥ ɞɨɪɿɜɧɸɜɚɬɢɦɟ ɪɿɡɧɢɰɿ ɣɦɨɜɿɪɧɨɫ-
ɬɟɣ Ɋ(Ⱥ
1
) ɿ Ɋ(Ⱥ
2
) ɩɨɞɿɣ Ⱥ
1
ɿ Ⱥ
2
, ɬɨɛɬɨ Ɋ(70 IQ
90) = Ɋ(IQ
90) – Ɋ(IQ
70).
ȼɢɡɧɚɱɟɧɧɹ ɣɦɨɜɿɪɧɨɫɬɿ ɡɚ ɞɨɩɨɦɨɝɨɸ ɮɭɧɤɰɿɣ ɪɨɡɩɨɞɿɥɭ ɦɚɬɢɦɟ ɜɢɝɥɹɞ:
)70()90()()()(
709090
70
FFdxxfdxxfdxxf
³³³
ff
, ɚɛɨ
F(90) – F(70) = 0,253 – 0,023 § 0,23.
Ɉɬɠɟ, ɣɦɨɜɿɪɧɿɫɬɶ Ɋ(70 IQ
90) § 23%.
103
Ɋɢɫ. 3.16. Ƀɦɨɜɿɪɧɿɫɬɶ
Ɋ(70 IQ
90) § 23%.
Ɋɢɫ. 3.17. Ƀɦɨɜɿɪɧɿɫɬɶ
Ɋ(80 IQ
>120) §18,2%.
ɝ) ȼɢɡɧɚɱɢɬɢ ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ IQ
ɩɪɢɣɦɚɬɢɦɟ ɡɧɚɱɟɧɧɹ ɩɨɡɚ ɦɟɠɚɦɢ
ɿɧɬɟɪɜɚɥɭ 80 < IQ
120, ɬɨɛɬɨ Ɋ(80 IQ
>120). ɐɿɣ ɩɨɞɿʀ ɜɿɞɩɨɜɿɞɚɽ ɫɭɦɚ ɞɜɨɯ
ɡɚɮɚɪɛɨɜɚɧɢɯ ɱɚɫɬɢɧ ɩɥɨɳɿ ɪɢɫ. 3.17. Ɋɿɲɟɧɧɹ ɦɨɠɧɚ ɨɬɪɢɦɚɬɢ ɭ 2-ɯ ɜɚɪɿɚɧ-
ɬɚɯ:
1-ɣ ɜɚɪɿɚɧɬ. ɉɨɞɿɹ Ⱥ ɫɤɥɚɞɚɽɬɶɫɹ ɡ ɞɜɨɯ ɧɟɫɭɦɿɫɧɢɯ ɩɨɞɿɣ Ⱥ
1
{IQ
80} ɿ
Ⱥ
2
{IQ
>120} ɡ ɣɦɨɜɿɪɧɨɫɬɹɦɢ Ɋ(Ⱥ
1
) ɿ Ɋ(Ⱥ
2
) ɜɿɞɩɨɜɿɞɧɨ.
Ƀɦɨɜɿɪɧɿɫɬɶ Ɋ(Ⱥ
1
) ɩɨɞɿʀ Ⱥ
1
ɜɢɡɧɚɱɢɬɶɫɹ ɹɤ
)80()(
80
Fdxxf
³
f
, ɚɛɨ ɡ ɬɚɛɥ. ɪɢɫ. 3.12 ɦɚɽɦɨ F(80) § 0,091.
Ƀɦɨɜɿɪɧɿɫɬɶ Ɋ(Ⱥ
2
) ɩɨɞɿʀ Ⱥ
2
ɜɢɡɧɚɱɢɬɶɫɹ ɹɤ ɞɨɩɨɜɧɟɧɧɹ ɞɨ ɩɪɨɬɢɥɟɠɧɨʀ
ɩɨɞɿʀ
}120{
2
dIQȺ
ɚɛɨ Ɋ(Ⱥ
2
) = 1 –
}120{
2
dIQȺ
, ɚ ɫɚɦɟ
)120(1)(1)120(
120
FdxxfxF !
³
f
ɚɛɨ
³
f
d !
120
)(1)120(1)120( dxxfxFxF
= 1 – 0,909 § 0,091.
Ƀɦɨɜɿɪɧɿɫɬɶ Ɋ(Ⱥ) ɩɨɞɿʀ Ⱥ ɫɤɥɚɞɚɽɬɶɫɹ ɡ ɫɭɦɢ ɣɦɨɜɿɪɧɨɫɬɟɣ Ɋ(Ⱥ
1
) ɿ Ɋ(Ⱥ
2
)
ɩɨɞɿɣ Ⱥ
1
ɿ Ⱥ
2
, ɬɨɛɬɨ Ɋ(Ⱥ) = Ɋ(Ⱥ
1
) + Ɋ(Ⱥ
2
) = 0,091 + 0,091 § 0,182 § 18,2%.
2-ɣ ɜɚɪɿɚɧɬ. ɉɨɞɿɸ Ⱥ{80IQ
>120} ɦɨɠɧɚ ɡɜɟɫɬɢ ɿ ɪɨɡɝɥɹɞɚɬɢ ɹɤ ɞɨɩɨɜ-
ɧɟɧɧɹ ɞɨ ɩɪɨɬɢɥɟɠɧɨʀ ɩɨɞɿʀ
Ⱥ
, ɹɤɭ ɩɨɡɧɚɱɢɦɨ ȼ{80 IQ 120} (ɞɢɜ. ɧɟɡɚɮɚ-
104
ɪɛɨɜɚɧɭ ɩɥɨɳɭ ɪɢɫ. 3.17). Ɍɨɞɿ Ɋ(Ⱥ) = 1– Ɋ(ȼ).
ɉɨɞɿɹ ȼ{80 IQ
120} ɜɿɞɩɨɜɿɞɚɽ ɩɨɩɟɪɟɞɧɿɣ ɫɢɬɭɚɰɿʀ (ɞɢɜ. ɜɢɳɟ ɩ. «ɜ»),
ɤɨɥɢ ɡ ɩɨɞɿʀ ȼ
1
{IQ
120} ɬɪɟɛɚ ɜɢɥɭɱɚɬɢ ɟɥɟɦɟɧɬɢ ɩɨɞɿʀ ȼ
2
{IQ
80}.
Ƀɦɨɜɿɪɧɿɫɬɶ Ɋ(ȼ) ɩɨɞɿʀ ȼ ɽ ɪɿɡɧɢɰɹ ɣɦɨɜɿɪɧɨɫɬɟɣ Ɋ(ȼ
1
) ɿ Ɋ(ȼ
2
)
Ɋ(ȼ) = Ɋ(IQ
120) – Ɋ(IQ
80).
Ƀɦɨɜɿɪɧɿɫɬɶ Ɋ(Ⱥ) ɛɚɠɚɧɨʀ ɩɨɞɿʀ Ⱥ ɞɨɪɿɜɧɸɜɚɬɢɦɟ
Ɋ(Ⱥ) = 1– Ɋ(ȼ) = 1 – [Ɋ(IQ
120) – Ɋ(IQ
80)].
ȼɢɡɧɚɱɟɧɧɹ ɣɦɨɜɿɪɧɨɫɬɿ ɡɚ ɞɨɩɨɦɨɝɨɸ ɮɭɧɤɰɿɣ ɪɨɡɩɨɞɿɥɭ ɦɚɬɢɦɟ ɜɢɝɥɹɞ:
>@
)80()120(1)()(1)(1
80120120
80
FFdxxfdxxfdxxf
»
¼
º
«
¬
ª
³³³
ff
, ɚɛɨ
1– [F(120) – F(80)] = 1 – [0,909 – 0,091] = 1– 0,818 § 0,182 § 18,2%.
Ɉɬɠɟ, ɣɦɨɜɿɪɧɿɫɬɶ ɬɨɝɨ, ɳɨ IQ
ɧɟ ɩɪɢɣɦɚɬɢɦɟ ɡɧɚɱɟɧɧɹ ɜ ɞɿɚɩɚɡɨɧɿ ɜɿɞ 80
ɞɨ 120, ɬɨɛɬɨ Ɋ(80 IQ
>120), ɫɤɥɚɞɚɽ 18,2%.
Ɂɚɭɜɚɠɟɧɧɹ: ɹɤɳɨ ɝɪɚɮɿɤ ɪɨɡɩɨɞɿɥɭ ɫɢɦɟɬɪɢɱɧɢɣ ɿ ɡɚɮɚɪɛɨɜɚɧɿ ɩɥɨɳɿ ɨɞ-
ɧɚɤɨɜɿ ɡɚ ɪɨɡɦɿɪɨɦ, ɣɦɨɜɿɪɧɿɫɬɶ Ɋ(Ⱥ) ɪɨɡɪɚɯɨɜɭɽɬɶɫɹ ɹɤ ɩɨɞɜɨɽɧɚ ɩɥɨɳɚ ɨɞɧɿ-
ɽʀ ɡ ɱɚɫɬɢɧ, ɧɚɩɪɢɤɥɚɞ, Ɋ(Ⱥ) = 2·Ɋ(80 IQ) = 2·0,091 § 0,182 § 18,2%.
Ɋɨɡɩɨɞɿɥɢ ɞɚɸɬɶ ɦɨɠɥɢɜɿɫɬɶ ɪɿɲɟɧɧɹ ɿ ɡɜɨɪɨɬɧɨʀ ɡɚɞɚɱɿ: ɡɧɚɯɨɞɠɟɧɧɹ ɡɧɚ-
ɱɟɧɶ ɡɦɿɧɧɨʀ ɏ, ɣɦɨɜɿɪɧɿɫɬɶ ɹɤɨʀ ɡɚɞɚɧɨ.
Ɍɚɤ, ɡɚ ɞɚɧɢɦɢ
ɩɪɢɤɥɚɞɭ 3.12 ɦɨɠɧɚ ɫɬɜɟɪɞɠɭɜɚɬɢ, ɳɨ ɧɚ ɪɿɜɧɿ ɣɦɨɜɿɪɧɨ-
ɫɬɿ 0,05 (5%) ɤɨɟɮɿɰɿɽɧɬ ɿɧɬɟɥɟɤɬɭ IQ ɧɟ ɩɟɪɟɜɢɳɭɜɚɬɢɦɟ ɡɧɚɱɟɧɧɹ 75,3. Ɂ
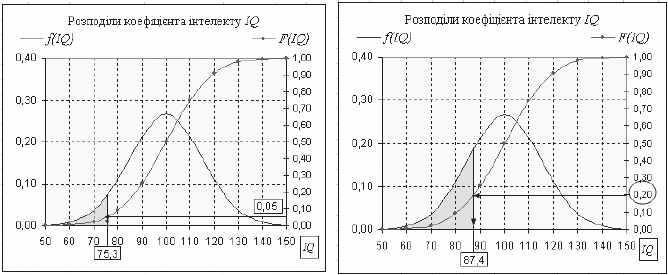
ɝɪɚɮɿɤɚ ɮɭɧɤɰɿʀ ɪɨɡɩɨɞɿɥɭ F(IQ) ɪɢɫ. 3.18 ɜɢɞɧɨ, ɳɨ ɣɦɨɜɿɪɧɨɫɬɿ 0,05 ɜɿɞɩɨ-
ɜɿɞɚɽ ɡɚɮɚɪɛɨɜɚɧɚ ɩɥɨɳɚ, ɹɤɚ ɨɛɦɟɠɟɧɚ ɝɪɚɮɿɤɨɦ ɳɿɥɶɧɨɫɬɿ f(IQ) ɿ ɨɪɞɢɧɚɬɨɸ
IQ = 75,3. ȱɧɚɤɲɟ ɤɚɠɭɱɢ, F(IQ) = Ɋ(IQ 75,3) = 0,05.
Ⱥɧɚɥɨɝɿɱɧɨ ɦɨɠɧɚ ɨɬɪɢɦɚɬɢ ɡɧɚɱɟɧɧɹ ɡɦɿɧɧɨʀ IQ, ɣɦɨɜɿɪɧɿɫɬɶ
ɹɤɨʀ ɫɤɥɚ-
ɞɚɽ 20% ɚɛɨ 0,20. Ɂ ɪɢɫ. 3.19 ɜɢɞɧɨ, ɳɨ ɣɦɨɜɿɪɧɨɫɬɿ 0,20 ɜɿɞɩɨɜɿɞɚɽ ɡɚɮɚɪɛɨ-
ɜɚɧɚ ɩɥɨɳɚ, ɹɤɚ ɨɛɦɟɠɟɧɚ ɝɪɚɮɿɤɨɦ ɳɿɥɶɧɨɫɬɿ f(IQ) ɿ ɨɪɞɢɧɚɬɨɸ IQ = 87,4.
ȱɧɚɤɲɟ ɤɚɠɭɱɢ, F(IQ) = Ɋ(IQ 87,4) = 0,20.
105
Ɋɢɫ. 3.18. Ƀɦɨɜɿɪɧɨɫɬɿ 0,05 ɜɿɞɩɨɜɿɞɚɽ
ɡɧɚɱɟɧɧɹ IQ 75,3
Ɋɢɫ. 3.19. Ƀɦɨɜɿɪɧɨɫɬɿ 0,20 ɜɿɞɩɨɜɿɞɚɽ
ɡɧɚɱɟɧɧɹ IQ 87,4
ɇɚ ɞɚɧɨɦɭ ɟɬɚɩɿ ɜɢɜɱɟɧɧɹ ɜɥɚɫɬɢɜɨɫɬɟɣ ɪɨɡɩɨɞɿɥɿɜ ɞɨɪɟɱɧɨ ɡɝɚɞɚɬɢ ɩɨ-
ɧɹɬɬɹ «ɩɪɨɰɟɧɬɢɥɶ» ɿ ɧɚɞɚɬɢ ɣɨɦɭ ɞɨɞɚɬɤɨɜɨɝɨ ɡɦɿɫɬɨɜɧɨɝɨ ɫɟɧɫɭ. əɤ ɜɢɡɧɚ-
ɱɚɥɨɫɹ ɜɢɳɟ, ɩɪɨɰɟɧɬɢɥɿ ɞɿɥɹɬɶ ɨɛɫɹɝ ɭɩɨɪɹɞɤɨɜɚɧɨʀ ɫɭɤɭɩɧɨɫɬɿ ɧɚ ɫɬɨ ɱɚɫ-
ɬɢɧ, ɬɨɛɬɨ ɜɿɞɨɤɪɟɦɥɸɸɬɶ ɜɿɞ ɫɭɤɭɩɧɨɫɬɿ ɩɨ 0,01 ɱɚɫɬɤɢ (ɩɨ 1%). Ɋ
ɿ
– ɰɟ ɿ-ɣ
ɩɪɨɰɟɧɬɢɥɶ – ɦɟɠɚ, ɧɢɠɱɟ ɡɚ ɹɤɭ ɥɟɠɚɬɶ ɿ ɜɿɞɫɨɬɤɿɜ ɡɧɚɱɟɧɶ. ɇɚɩɪɢɤɥɚɞ, ɹɤ-
ɳɨ ɩ’ɹɬɢɣ ɩɪɨɰɟɧɬɢɥɶ ɞɨɪɿɜɧɸɽ 30 (ɡɚɩɢɫɭɸɬɶ Ɋ
5
= 30), ɰɟ ɡɧɚɱɢɬɶ, ɳɨ 5%
ɜɫɿɯ ɡɧɚɱɟɧɶ ɏ ɧɟ ɩɟɪɟɜɢɳɭɸɬɶ 30.
Ɂɧɚɱɟɧɧɹ ɮɭɧɤɰɿʀ ɪɨɡɩɨɞɿɥɭ F(ɏ), ɹɤɿ ɡɧɚɯɨɞɹɬɶɫɹ ɭ ɦɟɠɚɯ ɜɿɞ 0 ɞɥɹ F(–)
ɞɨ 1 ɞɥɹ F(+), ɬɚɤɨɠ ɡɪɭɱɧɨ ɩɨɞɿɥɢɬɢ ɧɚ ɫɬɨ ɱɚɫɬɢɧ ɿ ɩɪɟɞɫɬɚɜɥɹɬɢ ɮɭɧɤɰɿɸ
ɪɨɡɩɨɞɿɥɭ ɭ ɜɢɝɥɹɞɿ ɩɪɨɰɟɧɬɢɥɿɜ. əɤɳɨ ɰɿɧɚ ɲɤɚɥɢ ɮɭɧɤɰɿʀ ɪɨɡɩɨɞɿɥɭ F(ɏ)
ɫɬɚɧɨɜɢɬɶ 0,01 (1%), ɨɬɪɢɦɚɧɿ ɜɢɳɟ ɪɟɡɭɥɶɬɚɬɢ ɦɨɠɧɚ ɩɪɨɤɨɦɟɧɬɭɜɚɬɢ
ɭ ɬɚɤɿɣ
ɫɩɨɫɿɛ:
x
ɞɥɹ F(IQ) = Ɋ(IQ75,3) = 0,05 = 5% ɦɨɠɧɚ ɡɚɩɢɫɚɬɢ Ɋ
5
= 75,3 – ɩ’ɹɬɨɦɭ
ɩɪɨɰɟɧɬɢɥɸ ɜɿɞɩɨɜɿɞɚɽ ɤɨɟɮɿɰɿɽɧɬ ɿɧɬɟɥɟɤɬɭ, ɹɤɢɣ ɧɟ ɩɟɪɟɜɢɳɭɽ ɡɧɚɱɟɧɧɹ ɭ 75,3;
x
ɞɥɹ F(IQ) = Ɋ(IQ 87,4) = 0,20 = 20% ɦɨɠɧɚ ɡɚɩɢɫɚɬɢ Ɋ
20
= 87,4 – ɞɜɚ-
ɞɰɹɬɨɦɭ ɩɪɨɰɟɧɬɢɥɸ ɜɿɞɩɨɜɿɞɚɽ ɤɨɟɮɿɰɿɽɧɬ ɿɧɬɟɥɟɤɬɭ, ɹɤɢɣ ɧɟ ɩɟɪɟɜɢɳɭɽ 87,4.
Ɂɧɚɱɟɧɧɹ ɩɪɨɰɟɧɬɢɥɹ ɞɥɹ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ ɦɨɠɧɚ ɨɬɪɢɦɚɬɢ ɡɚ ɞɨ-
ɩɨɦɨɝɨɸ ɮɭɧɤɰɿʀ MS Excel =ɇɈɊɆɈȻɊ(ɣɦɨɜɿɪɧɿɫɬɶ; ɫɟɪɟɞɧɽ; ɫɬ.ɜɿɞɯɢɥɟɧɧɹ).
Ɍɚɤ, Ɋ
5
= ɇɈɊɆɈȻɊ(0,05;100;15) = 75,3; ɚ Ɋ
20
= ɇɈɊɆɈȻɊ(0,20;100;15) = 87,4.

106
ɏɚɪɚɤɬɟɪɢɫɬɢɤɢ ɜɢɩɚɞɤɨɜɢɯ ɜɟɥɢɱɢɧ
ȼɢɩɚɞɤɨɜɭ ɜɟɥɢɱɢɧɭ ɏ ɦɨɠɧɚ ɩɨɜɧɨɰɿɧɧɨ ɯɚɪɚɤɬɟɪɢɡɭɜɚɬɢ ɮɭɧɤɰɿɽɸ ɪɨɡ-
ɩɨɞɿɥɭ ɩɨɞɿɣ Ȧ
ɿ
, (ɮɭɧɤɰɿɹ ɜɢɡɧɚɱɟɧɚ ɧɚ ɩɪɨɫɬɨɪɿ ɟɥɟɦɟɧɬɚɪɧɢɯ ɩɨɞɿɣ ȍ). Ɏɭ-
ɧɤɰɿɹ ɪɨɡɩɨɞɿɥɭ ɭ ɜɢɝɥɹɞɿ ɝɿɫɬɨɝɪɚɦɢ (ɞɥɹ ɞɢɫɤɪɟɬɧɨʀ ɡɦɿɧɧɨʀ) ɚɛɨ ɮɭɧɤɰɿʀ
ɳɿɥɶɧɨɫɬɿ (ɞɥɹ ɧɟɩɟɪɟɪɜɧɨʀ ɡɦɿɧɧɨʀ) ɞɚɽ ɜɢɱɟɪɩɧɭ ɿɧɮɨɪɦɚɰɿɸ ɳɨɞɨ ɡɚɤɨɧɭ
ɪɨɡɩɨɞɿɥɭ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ. ɉɪɨɬɟ ɫɩɨɫɬɟɪɿɝɚɸɬɶɫɹ ɡɚɜɠɞɢ ɬɿɥɶɤɢ ɡɧɚ-
ɱɟɧɧɹ ɰɿɽʀ ɮɭɧɤɰɿʀ, ɹɤɿ ɽ ɪɟɚɥɿɡɚɰɿɽɸ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɭ ɤɨɧɤɪɟɬɧɿɣ ɫɢɬɭ-
ɚɰɿʀ. ɋɚɦɚ ɠ ɮɭɧɤɰɿɹ ɪɨɡɩɨɞɿɥɭ ɽ ɥɢɲɟ ɬɟɨɪɟɬɢɱɧɢɦ ɭɡɚɝɚɥɶɧɟɧɧɹɦ, ɹɤɟ ɫɥɭ-
ɠɢɬɶ ɨɫɧɨɜɨɸ ɞɥɹ ɩɨɛɭɞɨɜɢ ɿɦɨɜɿɪɧɿɫɧɢɯ ɦɨɞɟɥɟɣ ɜɢɜɱɟɧɧɹ ɪɟɚɥɶɧɨɫɬɿ.
Ɋɟɡɭɥɶɬɚɬɢ ɜɢɩɪɨɛɭɜɚɧɶ, ɹɤ ɩɪɚɜɢɥɨ, ɦɨɞɟɥɸɸɬɶɫɹ ɧɟɡɚɥɟɠɧɢɦɢ ɜɢɩɚɞ-
ɤɨɜɢɦɢ ɜɟɥɢɱɢɧɚɦɢ. ɑɚɫɬɨ ɜɜɚɠɚɸɬɶ, ɳɨ ɫɩɨɫɬɟɪɟɠɟɧɧɹ, ɿɫɩɢɬɢ, ɞɨɫɥɿɞɢ
ɩɪɨɜɨɞɹɬɶɫɹ ɡɚ ɫɯɟɦɨɸ ɧɟɡɚɥɟɠɧɢɯ ɿɫɩɢɬɿɜ. Ɉɬɠɟ, ɧɟɡɚɥɟɠɧɿɫɬɶ ɜɢɩɚɞɤɨɜɢɯ
ɜɟɥɢɱɢɧ – ɨɞɧɟ ɡ ɛɚɡɨɜɢɯ ɩɨɧɹɬɶ ɬɟɨɪɿʀ ɣɦɨɜɿɪɧɨɫɬɟɣ, ɳɨ ɥɟɠɢɬɶ ɜ ɨɫɧɨɜɿ
ɩɪɚɤɬɢɱɧɨ ɜɫɿɯ ɣɦɨɜɿɪɧɨɫɧɨ-ɫɬɚɬɢɫɬɢɱɧɢɯ ɦɟɬɨɞɿɜ. Ɍɨɦɭ ɫɥɿɞ ɦɚɬɢ ɧɚ ɭɜɚɡɿ
ɞɟɹɤɿ ɜɚɠɥɢɜɿ ɜɥɚɫɬɢɜɨɫɬɿ ɧɟɡɚɥɟɠɧɢɯ ɜɢɩɚɞɤɨɜɢɯ ɜɟɥɢɱɢɧ:
x ɜɢɩɚɞɤɨɜɿ ɜɟɥɢɱɢɧɢ X ɿ Y, ɜɢɡɧɚɱɟɧɿ ɧɚ ɬɨɦɭ ɠ ɫɚɦɨɦɭ ɩɪɨɫɬɨɪɿ ɟɥɟɦɟ-
ɧɬɚɪɧɢɯ ɩɨɞɿɣ, ɧɚɡɢɜɚɸɬɶɫɹ ɧɟɡɚɥɟɠɧɢɦɢ, ɹɤɳɨ ɞɥɹ ɛɭɞɶ-ɹɤɢɯ ɱɢɫɟɥ ɚ ɿ b ɩɨ-
ɞɿʀ {X=a} ɿ {Y=b} ɽ ɧɟɡɚɥɟɠɧɢɦɢ;
x ɹɤɳɨ ɜɢɩɚɞɤɨɜɿ ɜɟɥɢɱɢɧɢ X ɿ Y ɧɟɡɚɥɟɠɧɿ, ɚ ɿ b - ɞɟɹɤɿ ɱɢɫɥɚ, ɬɨ ɜɢɩɚɞ-
ɤɨɜɿ ɜɟɥɢɱɢɧɢ X+a ɿ Y+b ɬɚɤɨɠ ɧɟɡɚɥɟɠɧɿ;
x ɹɤɳɨ ɜɢɩɚɞɤɨɜɿ ɜɟɥɢɱɢɧɢ X ɿ Y ɧɟɡɚɥɟɠɧɿ, ɚ f(X) ɿ g(Y) – ɜɢɩɚɞɤɨɜɿ ɜɟ-
ɥɢɱɢɧɢ, ɨɬɪɢɦɚɧɿ ɡ X ɿ Y ɡɚ ɞɨɩɨɦɨɝɨɸ ɞɟɹɤɢɯ ɮɭɧɤɰɿɣ f ɿ g, ɬɨ f(X) ɿ g(Y) – ɬɚ-
ɤɨɠ ɧɟɡɚɥɟɠɧɿ ɜɢɩɚɞɤɨɜɿ ɜɟɥɢɱɢɧɢ. ɇɚɩɪɢɤɥɚɞ, ɹɤɳɨ X ɿ Y ɧɟɡɚɥɟɠɧɿ, ɬɨ ɏ
2
ɿ
3·Y +4 ɧɟɡɚɥɟɠɧɿ, ɚ ɬɚɤɨɠ ln(X ) ɿ ln(Y) ɧɟɡɚɥɟɠɧɿ.
ɍ ɩɪɚɤɬɢɰɿ ɞɨɫɥɿɞɠɭɜɚɧɧɹ ɝɟɧɟɪɚɥɶɧɨʀ ɫɭɤɭɩɧɨɫɬɿ ɰɿɥɤɨɦ ɞɨɫɬɚɬɧɿɦ ɽ
ɨɬɪɢɦɚɧɧɹ ɞɟɤɿɥɶɤɨɯ ɱɢɫɟɥɶɧɢɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ, ɳɨ ɨɰɿɧɸɸɬɶ ɰɟɧɬɪ ɝɪɭɩɭ-
ɜɚɧɧɹ ɡɧɚɱɟɧɶ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ, ɦɿɪɭ ʀɯɧɶɨɝɨ ɪɨɡɫɿɹɧɧɹ, ɫɬɭɩɿɧɶ ɜɡɚɽɦɨ-
ɡɜ’ɹɡɤɭ ɪɿɡɧɢɯ ɤɨɦɩɨɧɟɧɬɿɜ ɛɚɝɚɬɨɦɿɪɧɨʀ ɨɡɧɚɤɢ. ɍ ɫɜɨɸ ɱɟɪɝɭ, ɡɧɚɸɱɢ ɥɢɲɟ
ɯɚɪɚɤɬɟɪ ɫɬɚɬɢɫɬɢɱɧɢɯ ɡɚɤɨɧɿɜ, ɪɨɡɩɨɞɿɥ ɦɨɠɟ ɛɭɬɢ ɭɫɩɿɲɧɨ ɜɿɞɧɨɜɥɟɧɨ ɡɚ
ɫɜɨʀɦɢ ɱɢɫɟɥɶɧɢɦɢ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚɦɢ, ɧɚɩɪɢɤɥɚɞ, ɡɚ ɫɟɪɟɞɧɿɦɢ ɡɧɚɱɟɧɧɹɦɢ,

107
ɞɢɫɩɟɪɫɿɽɸ. Ɍɨɠ ɞɨɰɿɥɶɧɨ ɪɨɡɝɥɹɧɭɬɢ ɨɫɧɨɜɧɿ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɜɢɩɚɞɤɨɜɨʀ ɜɟ-
ɥɢɱɢɧɢ ɏ, ɳɨ ɞɚɸɬɶ ɡɦɨɝɭ ɱɢɫɟɥɶɧɨ ɨɰɿɧɢɬɢ ɬɚɤ ɡɜɚɧɿ ɩɨɤɚɡɧɢɤɢ «ɰɟɧɬɪɚɥɶ-
ɧɨʀ ɬɟɧɞɟɧɰɿʀ» (ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ Ɇ[X], ɦɨɞɭ Ɇo[X] ɿ ɦɟɞɿɚɧɭ Ɇd[X]), ɚ
ɬɚɤɨɠ «ɜɚɪɿɚɬɢɜɧɨɫɬɿ» (ɞɢɫɩɟɪɫɿɹ D[X], ɫɬɚɧɞɚɪɬɧɟ ɜɿɞɯɢɥɟɧɧɹ SD[X]) .
Ɇɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ. Ɉɞɧɿɽɸ ɡ ɜɚɠɥɢɜɢɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɪɨɡɩɨɞɿɥɭ
ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɏ ɽ ʀʀ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ Ɇ[X] (ɿɧɨɞɿ ɣɨɝɨ ɧɚɡɢ-
ɜɚɸɬɶ ɫɟɪɟɞɧɽ ɡɧɚɱɟɧɧɹ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ).
Ɉɡɧɚɱɟɧɧɹ. Ɇɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɽ ɱɢɫɥɨ
¦
:
Z
Z
Z
)()(][ PXXM , (3.21)
ɞɟ ɏ(Ȧ) – ɡɧɚɱɟɧɧɹ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɏ, ɨɬɪɢɦɚɧɟ ɭ ɩɨɞɿʀ Ȧ; Ɋ(Ȧ) –
ɣɦɨɜɿɪɧɿɫɬɶ ɜɢɩɚɞɤɨɜɨʀ ɩɨɞɿʀ Ȧ; ȍ – ɩɪɨɫɬɿɪ ɟɥɟɦɟɧɬɚɪɧɢɯ ɩɨɞɿɣ Ȧȍ.
ɉɪɢɤɥɚɞ 3.13. Ɉɛɱɢɫɥɢɬɢ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ ɱɢɫɥɚ, ɳɨ ɜɢɩɚɞɚɽ ɧɚ
ɜɟɪɯɧɿɣ ɝɪɚɧɿ ɿɝɪɨɜɨɝɨ ɤɭɛɢɤɚ.
Ɋɿɲɟɧɧɹ:
ɉɪɨɫɬɿɪ ȍ ɫɤɥɚɞɚɽɬɶɫɹ ɡ 6 ɟɥɟɦɟɧɬɚɪɧɢɯ ɩɨɞɿɣ {Ȧ
1
, Ȧ
2
, …, Ȧ
6
}. Ʉɨɠɧɿɣ
ɟɥɟɦɟɧɬɚɪɧɿɣ ɩɨɞɿʀ ɜɿɞɩɨɜɿɞɚɽ ɡɧɚɱɟɧɧɹ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ. Ⱦɥɹ ɿɝɪɨɜɨɝɨ
ɤɭɛɢɤɚ ɰɟ ɱɢɫɥɨ ɜɿɞ 1 ɞɨ 6 ɧɚ ɣɨɝɨ ɝɪɚɧɹɯ: X(Ȧ
1
) = 1, X(Ȧ
2
) = 2, ... X(Ȧ
6
) = 6.
ȼɫɿ ɩɨɞɿʀ ɦɚɸɬɶ ɪɿɜɧɿ ɣɦɨɜɿɪɧɨɫɬɿ ɜɿɞɛɭɬɢɫɹ Ɋ(Ȧ
1
) = Ɋ(Ȧ
2
) =... Ɋ(Ȧ
6
) = 1/6.
Ɂɜɿɞɫɢ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɞɨɪɿɜɧɸɜɚɬɢɦɟ:
5,3
6
21
6
1
6
6
1
5
6
1
4
6
1
3
6
1
2
6
1
1)()(][
¦
:
Z
ZZ
PXXM .
ȼɿɞɩɨɜɿɞɶ: ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ Ɇ[X]=3,5.
Ɇɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ ɩɪɨɫɬɨʀ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ X ɡ ɦɧɨɠɢɧɨɸ ɡɧɚ-
ɱɟɧɶ ɏ(ȍ)= {x
1
, x
2
, …, x
n
} ɜɢɡɧɚɱɚɽɬɶɫɹ ɹɤ
¦
n
ɿ
ɿɿ
ɯɏɊɯXM
1
)(][ . (3.22)
ɋɟɧɫ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ ɜɚɪɬɨ ɪɨɡɤɪɢɬɢ ɧɚ ɩɪɢɤɥɚɞɿ.
ɉɪɢɤɥɚɞ 3.14. ɋɟɪɟɞɧɹ ɤɿɥɶɤɿɫɬɶ ɜɢɤɨɧɚɧɢɯ ɬɟɫɬɨɜɢɯ ɡɚɜɞɚɧɶ, ɳɨ ɩɪɢɩɚ-
ɞɚɽ ɧɚ ɨɞɧɨɝɨ ɫɬɭɞɟɧɬɚ, ɦɨɠɟ ɩɟɜɧɢɦ ɱɢɧɨɦ ɯɚɪɚɤɬɟɪɢɡɭɜɚɬɢ ɹɤɿɫɬɶ ɧɚɜɱɚɧ-
ɧɹ. ɐɟ ɦɨɠɧɚ ɩɪɢɣɧɹɬɢ, ɹɤɳɨ ɩɪɢɩɭɫɬɢɬɢ, ɳɨ ɨɤɪɟɦɿ ɡɧɚɱɟɧɧɹ ɜɢɩɚɞɤɨɜɨʀ
108
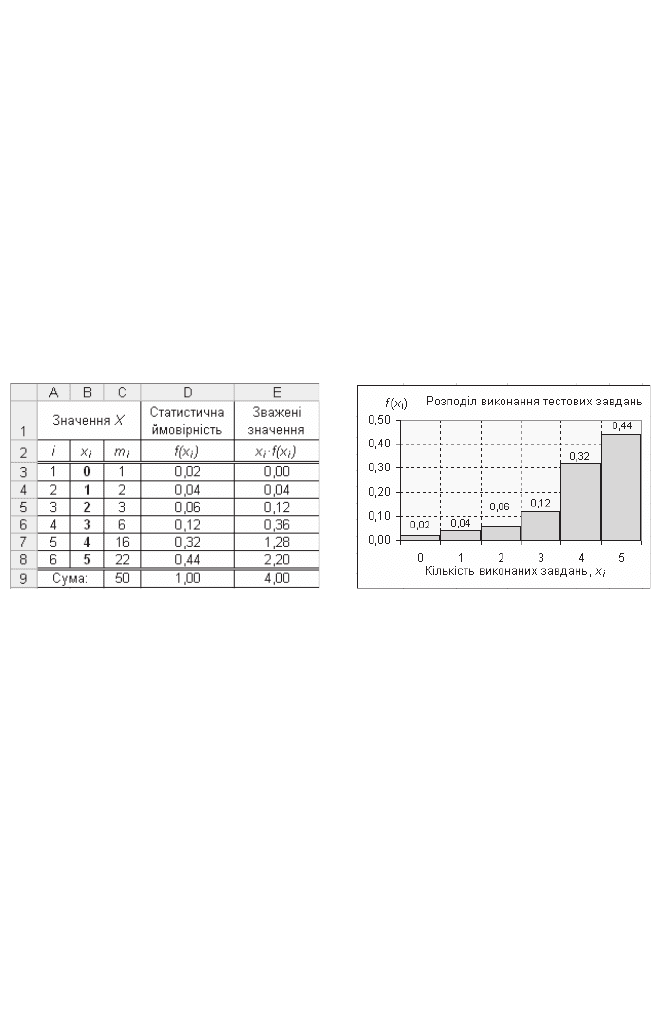
ɡɦɿɧɧɨʀ ɏ ɝɪɭɩɭɸɬɶɫɹ ɛɿɥɹ ɰɶɨɝɨ ɫɟɪɟɞɧɶɨɝɨ ɩɨɤɚɡɧɢɤɚ. ɍ ɬɚɛɥ. ɪɢɫ. 3.20 ɧɚ-
ɜɟɞɟɧɨ ɞɚɧɿ ɿɫɩɢɬɿɜ: x
ɿ
– ɦɨɠɥɢɜɚ ɤɿɥɶɤɿɫɬɶ ɜɢɤɨɧɚɧɢɯ ɡɚɜɞɚɧɶ ɡ ɩ’ɹɬɢ ɡɚɩɪɨ-
ɩɨɧɨɜɚɧɢɯ; m
ɿ
– ɜɿɞɩɨɜɿɞɧɚ ɤɿɥɶɤɿɫɬɶ ɜɢɤɨɧɚɧɶ (
¦
mm
i
). ɇɟɨɛɯɿɞɧɨ ɪɨɡɪɚ-
ɯɭɜɚɬɢ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ ɹɤ ɨɪɿɽɧɬɨɜɧɢɣ ɩɨɤɚɡɧɢɤ ɧɚɜɱɚɥɶɧɢɯ ɞɨɫɹɝ-
ɧɟɧɶ ɫɬɭɞɟɧɬɿɜ ɚɛɨ ɹɤɨɫɬɿ ɧɚɜɱɚɧɧɹ.
Ɋɿɲɟɧɧɹ:
x ɍ ɫɬɨɜɩɱɢɤɭ D (ɪɢɫ. 3.20) ɞɥɹ ɤɨɠɧɨɝɨ ɡɧɚɱɟɧɧɹ ɯ
ɿ
ɪɨɡɪɚɯɭɜɚɬɢ ɜɿɞɧɨɫɧɿ
ɱɚɫɬɨɬɢ f
i
= m
i
/m, ɩɪɢɣɧɹɜɲɢ ʀɯ ɡɚ ɫɬɚɬɢɫɬɢɱɧɿ ɣɦɨɜɿɪɧɨɫɬɿ Ɋ
ɿ
(ɏ = ɯ
ɿ
). Ɍɚɤɟ
ɩɪɢɩɭɳɟɧɧɹ ɫɩɪɚɜɟɞɥɢɜɟ ɩɪɢ ɜɟɥɢɤɿɣ ɤɿɥɶɤɨɫɬɿ ɜɢɩɪɨɛɭɜɚɧɶ.
x ɍ ɫɬɨɜɩɱɢɤɭ ȿ (ɪɢɫ. 3. 20) ɪɨɡɪɚɯɭɜɚɬɢ ɡɜɚɠɟɧɿ ɡɧɚɱɟɧɧɹ ɯ
ɿ
·f
i
.
x ɉɨɛɭɞɭɜɚɬɢ ɝɪɚɮɿɤ ɪɨɡɩɨɞɿɥɭ ɜɢɤɨɧɚɧɧɹ ɬɟɫɬɨɜɢɯ ɡɚɜɞɚɧɶ (ɪɢɫ. 3.21 ).
Ɋɢɫ. 3.20. Ɋɨɡɪɚɯɭɧɤɢ ɪɨɡɩɨɞɿɥɭ
ɜɢɤɨɧɚɧɧɹ ɬɟɫɬɨɜɢɯ ɡɚɜɞɚɧɶ
Ɋɢɫ. 3.21. Ƚɪɚɮɿɤ ɪɨɡɩɨɞɿɥɭ
ɜɢɤɨɧɚɧɧɹ ɬɟɫɬɨɜɢɯ ɡɚɜɞɚɧɶ
x Ɋɨɡɪɚɯɭɜɚɬɢ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ:
00,444,0532,0412,0306,0204,0102,00)(][
1
¦
n
ɿ
ɿɿ
ɯfɯXM
.
ȼɿɞɩɨɜɿɞɶ: ɫɟɪɟɞɧɽ ɡɧɚɱɟɧɧɹ ɤɿɥɶɤɨɫɬɿ ɜɢɤɨɧɚɧɢɯ ɡɚɜɞɚɧɶ, ɡɞɨɛɭɬɟ ɡɚ ɪɟ-
ɡɭɥɶɬɚɬɚɦɢ ɿɫɩɢɬɿɜ, ɛɥɢɡɶɤɟ ɞɨ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ Ɇ[X] = 4,00 ɿ ɦɨɠɟ
ɫɥɭɠɢɬɢ ɨɪɿɽɧɬɨɜɧɢɦ ɩɨɤɚɡɧɢɤɨɦ ɹɤɨɫɬɿ ɧɚɜɱɚɧɧɹ.
Ⱦɥɹ ɧɟɩɟɪɟɪɜɧɨʀ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɏ, ɹɤɳɨ ɮɭɧɤɰɿɹ ɪɨɡɩɨɞɿɥɭ F(x) ɚɛ-
ɫɨɥɸɬɧɨ ɧɟɩɟɪɟɪɜɧɚ ɿ ɧɟɜɿɞ'ɽɦɧɚ, ɮɭɧɤɰɿɹ f(x) ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ ɬɚɤɚ, ɳɨ
³
f
ɯ
dxxfxF )()(
. (3.23)
Ɍɨɞɿ ɦɚɬɟɦɚɬɢɱɧɢɦ ɫɩɨɞɿɜɚɧɧɹɦ ɧɚɡɢɜɚɽɬɶɫɹ ɱɢɫɥɨ
109
³
f
f
dxxfxXM )(][
. (3.24)
ɉɪɢɤɥɚɞ 3.15. Ɋɨɡɪɚɯɭɜɚɬɢ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ ɧɟɩɟɪɟɪɜɧɨʀ ɜɢɩɚɞɤɨ-
ɜɨʀ ɜɟɥɢɱɢɧɢ ɏ ɡ ɪɿɜɧɨɦɿɪɧɿɦ ɪɨɡɩɨɞɿɥɨɦ ɿɦɨɜɿɪɧɨɫɬɿ ɧɚ ɜɿɞɪɿɡɤɭ [a, b].
Ɋɿɲɟɧɧɹ:
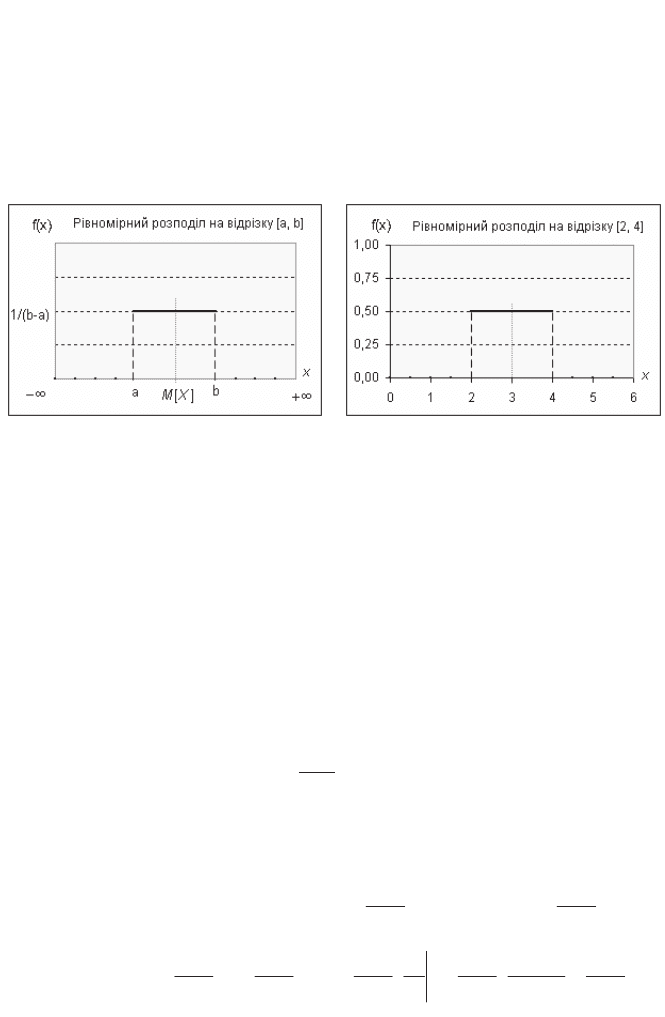
ɇɚ ɪɢɫ. 3.22. ɡɨɛɪɚɠɟɧɨ ɝɪɚɮɿɤ ɪɿɜɧɨɦɿɪɧɨɝɨ ɪɨɡɩɨɞɿɥɭ ɏ ɧɚ ɜɿɞɪɿɡɤɭ [a, b].
Ɋɢɫ. 3.22. Ƚɪɚɮɿɤ ɪɨɡɩɨɞɿɥɭ ɜɢɩɚɞɤɨɜɨʀ
ɜɟɥɢɱɢɧɢ
ɏ ɧɚ ɜɿɞɪɿɡɤɭ [a, b]
Ɋɢɫ. 3.23. Ƚɪɚɮɿɤ ɪɨɡɩɨɞɿɥɭ ɜɢɩɚɞɤɨɜɨʀ
ɜɟɥɢɱɢɧɢ ɏ ɧɚ ɜɿɞɪɿɡɤɭ [2, 4]
Ɇɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ M[X] ɪɨɡɪɚɯɨɜɭɽɬɶɫɹ ɹɤ ɜɢɡɧɚɱɧɢɣ ɿɧɬɟɝɪɚɥ ɧɚ
ɜɿɞɪɿɡɤɭ ɜɿɞ – ɞɨ +, ɚ ɫɚɦɟ
³
f
f
dxxfxXM )(][ .
ɓɿɥɶɧɿɫɬɶ ɪɿɜɧɨɦɿɪɧɨɝɨ ɪɨɡɩɨɞɿɥɭ f(x) ɧɚ ɜɿɞɪɿɡɤɭ [–, +] ɦɨɠɧɚ ɜɢɡɧɚ-
ɱɢɬɢ ɧɚ ɬɪɶɨɯ ɨɤɪɟɦɢɯ ɞɿɥɹɧɤɚɯ ɡɧɚɱɟɧɶ ɚɪɝɭɦɟɧɬɭ ɯ:
°
°
¯
°
°
®
fd
dd
df
.,0
;,
1
;,0
)(
xb
bxa
ab
ax
xf
.
Ɂɜɿɞɫɢ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ M[X] ɪɨɡɪɚɯɨɜɭɽɬɶɫɹ ɡɚ ɮɨɪɦɭɥɨɸ
³³³³³
f
f
f
f
b
ab
b
a
a
dx
ab
xdxxdx
ab
xdxxdxxfxXM
1
0
1
0)(][
ɚɛɨ
22
1
2
111
][
222
abab
ab
x
ab
xdx
ab
dx
ab
xXM
b
a
b
a
b
a
³³
.

110
ȼɿɞɩɨɜɿɞɶ: ɭ ɡɚɝɚɥɶɧɨɦɭ ɜɢɝɥɹɞɿ ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿɜɚɧɧɹ
2
][
ab
XM
. Ⱦɥɹ
ɤɨɧɤɪɟɬɧɢɯ ɡɧɚɱɟɧɶ ɜɿɞɪɿɡɤɭ [a, b], ɧɚɩɪɢɤɥɚɞ, a = 2 ɿ b = 4, ɦɚɬɟɦɚɬɢɱɧɟ ɫɩɨɞɿ-
ɜɚɧɧɹ 3
2
24
][
XM . ɇɚ ɪɢɫ. 3.23. ɡɨɛɪɚɠɟɧɨ ɝɪɚɮɿɤ ɪɿɜɧɨɦɿɪɧɨɝɨ ɪɨɡɩɨɞɿɥɭ
ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɏ ɧɚ ɜɿɞɪɿɡɤɭ [2, 4] ɿ ɜɿɞɦɿɱɟɧɨ ɩɨɥɨɠɟɧɧɹ M[X] = 3.
ȿɦɩɿɪɢɱɧɢɦ (ɬɨɛɬɨ ɩɨɛɭɞɨɜɚɧɢɦ ɡɚ ɜɢɛɿɪɤɨɜɢɦɢ ɞɚɧɢɦɢ ɯ
1
, ɯ
2
, …, ɯ
n
) ɚɧɚɥɨ-
ɝɨɦ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ ɽ ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ
¦
n
i
i
x
n
X
1
1
.
ɉɨɹɫɧɟɧɧɹ ɬɚɤɨɝɨ ɩɟɪɟɯɨɞɭ ɜɿɞ ɬɟɨɪɟɬɢɱɧɢɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɞɨ ɟɦɩɿɪɢɱɧɢɯ
(ɧɚɩɪɢɤɥɚɞ, ɜɿɞ ɦɚɬɟɦɚɬɢɱɧɨɝɨ ɫɩɨɞɿɜɚɧɧɹ M[X]) ɞɨ ɫɟɪɟɞɧɶɨɝɨ X ) ɛɚɡɭɽɬɶɫɹ ɧɚ
ɿɧɬɟɪɩɪɟɬɚɰɿʀ ɜɢɛɿɪɤɢ ɹɤ ɡɦɟɧɲɟɧɨʀ ɦɨɞɟɥɿ ɝɟɧɟɪɚɥɶɧɨʀ ɫɭɤɭɩɧɨɫɬɿ, ɞɟ ɦɨɠɥɢ-
ɜɢɦɢ ɡɧɚɱɟɧɧɹɦɢ ɽ ɜɢɛɿɪɤɨɜɿ ɡɧɚɱɟɧɧɹ, ɚ ɣɦɨɜɿɪɧɨɫɬɹɦɢ – ɜɿɞɧɨɫɧɿ ɱɚɫɬɨɬɢ ʀɯ
ɩɨɹɜɢ ɭ ɜɢɛɿɪɰɿ.
Ɋɨɡɩɨɞɿɥɢ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ ɏ ɦɨɠɭɬɶ ɛɭɬɢ ɨɯɚɪɚɤɬɟɪɢɡɨɜɚɧɿ ɳɟ ɞɜɨ-
ɦɚ ɦɿɪɚɦɢ ɩɨɥɨɠɟɧɧɹ ɰɟɧɬɪɭ: ɦɨɞɨɸ Ɇɨ[X] ɿ ɦɟɞɿɚɧɨɸ Md[X].
Ɉɡɧɚɱɟɧɧɹ. Ɇɨɞɨɸ Ɇɨ[X] ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ X ɧɚɡɢɜɚɸɬɶ ɬɚɤɟ ʀʀ ɡɧɚ-
ɱɟɧɧɹ, ɩɪɢ ɹɤɨɦɭ ɳɿɥɶɧɿɫɬɶ ɣɦɨɜɿɪɧɨɫɬɿ ɞɨɫɹɝɚɽ ɦɚɤɫɢɦɭɦɭ
13
.
Ⱦɥɹ ɞɢɫɤɪɟɬɧɨʀ ɜɟɥɢɱɢɧɢ ɦɨɞɨɸ ɽ ɧɚɣɛɿɥɶɲ ɿɦɨɜɿɪɧɟ ɡɧɚɱɟɧɧɹ ɜɢɩɚɞɤɨ-
ɜɨʀ ɜɟɥɢɱɢɧɢ. ɇɚɩɪɢɤɥɚɞ, ɡ ɪɢɫ. 3.21 ɦɨɠɧɚ ɜɫɬɚɧɨɜɢɬɢ, ɳɨ ɦɚɤɫɢɦɚɥɶɧɭ
ɣɦɨɜɿɪɧɿɫɬɶ 0,44 ɦɚɽ ɡɧɚɱɟɧɧɹ 5. Ɉɬɠɟ, ɰɟ ɡɧɚɱɟɧɧɹ ɿ ɽ ɦɨɞɨɸ Ɇɨ[X] = 5,00.
əɤɳɨ ɦɚɤɫɢɦɭɦ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ ɫɩɨɫɬɟɪɿɝɚɽɬɶɫɹ ɥɢɲɟ ɞɥɹ ɨɞɧɨɝɨ
ɡɧɚɱɟɧɧɹ ɡɦɿɧɧɨʀ X (ɪɢɫ. 3.21), ɪɨɡɩɨɞɿɥ ɧɚɡɢɜɚɽɬɶɫɹ ɭɧɿɦɨɞɚɥɶɧɢɦ (ɨɞɧɨɦɨ-
ɞɚɥɶɧɢɦ), ɹɤɳɨ ɞɥɹ ɞɟɤɿɥɶɤɨɯ ɧɟɫɭɫɿɞɧɿɯ ɡɧɚɱɟɧɶ – ɩɨɥɿɦɨɞɚɥɶɧɢɣ. Ɇɨɞɚ ɽ
ɩɪɢɪɨɞɧɨɸ ɯɚɪɚɤɬɟɪɢɫɬɢɤɨɸ ɰɟɧɬɪɚ ɝɪɭɩɭɜɚɧɧɹ ɭ ɪɚɡɿ ɭɧɿɦɨɞɚɥɶɧɢɯ ɪɨɡɩɨ-
ɞɿɥɿɜ. ɉɨɥɿɦɨɞɚɥɶɧɿ ɪɨɡɩɨɞɿɥɢ ɫɜɿɞɱɚɬɶ ɩɪɨ ɫɭɬɬɽɜɭ ɧɟɨɞɧɨɪɿɞɧɿɫɬɶ ɫɭɤɭɩɧɨ-
ɫɬɟɣ. Ȳɯɧɽ ɜɢɜɱɟɧɧɹ ɞɨɰɿɥɶɧɟ ɞɥɹ ɡɚɜɞɚɧɶ ɤɥɚɫɢɮɿɤɚɰɿʀ ɨɛ’ɽɤɬɿɜ ɞɨɫɥɿɞɠɟɧɧɹ.
Ⱦɥɹ ɧɟɩɟɪɟɪɜɧɨʀ ɜɟɥɢɱɢɧɢ ɦɨɞɭ Ɇɨ[X], ɹɤ ɦɚɤɫɢɦɭɦ ɳɿɥɶɧɨɫɬɿ (ɪɢɫ. 3.24),
13
qÔÒÓÒѾÐÒ ÓÒÔÈÑÅÖÍ ÙÊ ÒÌÑÆÚÊÑÑÅ Ì ÒÌÑÆÚÊÑÑÅÐ ÈÍÇÔ±ÒÈÒ ÐÒÉÍ nÒ.
