Руденко В.М. Математична статистика

Подождите немного. Документ загружается.

141

Ɂ ɦɚɬɟɦɚɬɢɱɧɨʀ ɬɨɱɤɢ ɡɨɪɭ ɧɟɨɛɯɿɞɧɨ ɜɢɡɧɚɱɢɬɢ ɬɚɤɟ z, ɹɤɟ ɨɛɦɟɠɭɽ ɨɪ-

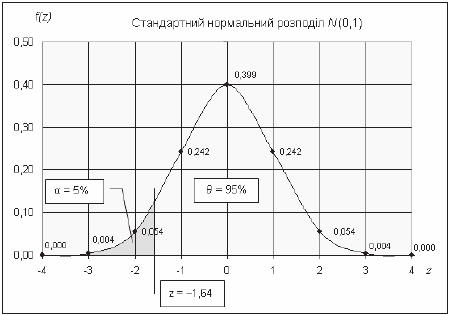
ɞɢɧɚɬɨɸ ɡɥɿɜɚ 5% ɩɥɨɳɿ ɩɿɞ ɧɨɪɦɚɥɶɧɨɸ ɤɪɢɜɨɸ (ɞɢɜ. ɪɢɫ. 3.47).

Ɋɢɫ. 3.47. Ɋɨɡɩɨɞɿɥ

N(0,1) ɦɚɽ ɩɚɪɚɦɟɬɪ z

0,05

§ –1,64

Ɍɪɚɞɢɰɿɣɧɨ ɰɟ ɡɚɜɞɚɧɧɹ ɬɚɤɨɠ ɜɢɪɿɲɭɜɚɥɨɫɹ ɡɚ ɞɨɩɨɦɨɝɨɸ ɫɩɟɰɿɚɥɶɧɢɯ

ɫɬɚɬɢɫɬɢɱɧɢɯ ɬɚɛɥɢɰɶ. ɉɪɨɬɟ, ɦɨɠɧɚ ɡɚɩɪɨɩɨɧɭɜɚɬɢ ɜɢɤɨɪɢɫɬɨɜɭɜɚɬɢ ɮɭɧɤ-

ɰɿɸ MS Excel =ɇɈɊɆɈȻɊ(

ɪ; ȝ; ı), ɹɤɚ ɩɨɜɟɪɬɚɽ ɡɧɚɱɟɧɧɹ z ɞɥɹ ɡɚɞɚɧɢɯ ɣɦɨ-

ɜɿɪɧɨɫɬɿ

ɪ, ɫɟɪɟɞɧɶɨɝɨ ȝ, ɫɬɚɧɞɚɪɬɧɨɝɨ ɜɿɞɯɢɥɟɧɧɹ ı. Ɍɚɤ, ɞɥɹ ɪ0,05, ȝ = 0 ɿ ı

= 1 ɮɭɧɤɰɿɹ =ɇɈɊɆɈȻɊ(0,05; 0; 1) ɩɨɜɟɪɧɟ ɡɧɚɱɟɧɧɹ

z § –1,64485. Ⱥɧɚɥɨɝɿɱ-

ɧɨ ɞɥɹ

ɪ0,01 =ɇɈɊɆɈȻɊ(0,01;0;1) ɩɨɜɟɪɧɟ ɡɧɚɱɟɧɧɹ z § –2,32635 ɿ ɬ.ɞ.

Ⱦɥɹ ɛɟɡɥɿɱɿ ɧɨɪɦɚɥɶɧɢɯ ɤɪɢɜɢɯ, ɳɨ ɜɿɞɪɿɡɧɹɸɬɶɫɹ ɨɞɢɧ ɜɿɞ ɨɞɧɨɝɨ ɡɧɚ-

ɱɟɧɧɹɦɢ

ȝ ɿ ı, ɜɚɠɥɢɜɨɸ ɡɚɝɚɥɶɧɨɸ ɜɥɚɫɬɢɜɿɫɬɸ ɽ ɬɟ, ɳɨ ɛɭɞɶ-ɹɤɚ ɱɚɫɬɢɧɚ

ɩɥɨɳɿ (ɹɤɚ ɚɫɨɰɿɸɽ ɣɦɨɜɿɪɧɿɫɬɶ) ɩɿɞ ɧɨɪɦɚɥɶɧɨɸ ɤɪɢɜɨɸ ɦɨɠɟ ɛɭɬɢ ɜɢɪɚɠɟ-

ɧɚ ɜ ɫɟɪɟɞɧɿɯ

ȝ ɿ ɫɬɚɧɞɚɪɬɧɢɯ ɜɿɞɯɢɥɟɧɧɹɯ ı. ɇɚɩɪɢɤɥɚɞ, ɜ ɛɭɞɶ-ɹɤɨɦɭ ɧɨɪɦɚ-

ɥɶɧɨɦɭ ɪɨɡɩɨɞɿɥɿ ɩɪɢɛɥɢɡɧɨ

95% ɩɥɨɳɿ ɩɿɞ ɤɪɢɜɨɸ ɥɟɠɢɬɶ ɜ ɦɟɠɚɯ ɞɜɨɯ ı

ɜɿɞ ɫɟɪɟɞɧɶɨɝɨ

ȝ (ɹɤɳɨ ɬɨɱɧɨ ɜɢɡɧɚɱɚɬɢ, ɬɨ 95% ɩɥɨɳɿ ɥɟɠɢɬɶ ɜ ɦɟɠɚɯ ɫɟɪɟ-

ɞɧɶɨɝɨ

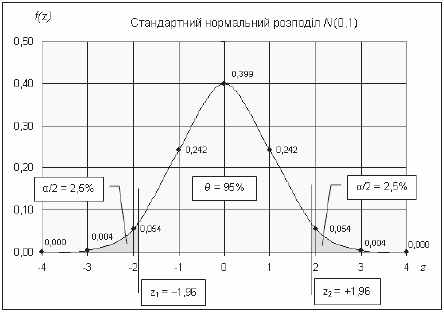
ȝ ɜɿɞ –1,96ı ɞɨ +1,96ı (ɞɢɜ. ɪɢɫ. 3.48);

142

Ɋɢɫ. 3.48. Ɋɨɡɩɨɞɿɥ

N(0,1) ɦɚɽ ɩɚɪɚɦɟɬɪ |z

0,025

| § 1,96

ȼɚɠɥɢɜɿɫɬɶ ɜɢɤɨɪɢɫɬɚɧɧɹ ɜ ɪɿɡɧɨɦɚɧɿɬɧɢɯ ɩɟɞɚɝɨɝɿɱɧɢɯ ɿ ɩɫɢɯɨɥɨɝɿɱɧɢɯ

ɞɨɫɥɿɞɠɟɧɧɹɯ

ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ ɩɨɹɫɧɸɽɬɶɫɹ ɜɢɫɧɨɜɤɚɦɢ ɰɟɧɬɪɚɥɶɧɨʀ

ɝɪɚɧɢɱɧɨʀ ɬɟɨɪɟɦɢ

, ɹɤɚ ɽ ɮɭɧɞɚɦɟɧɬɚɥɶɧɢɦ ɩɪɨɹɜɨɦ ɡɚɤɨɧɭ ɜɟɥɢɤɢɯ ɱɢɫɟɥ.

Ɇɿɠ ɬɢɦ ɜ ɤɨɧɤɪɟɬɧɢɯ ɩɪɢɤɥɚɞɧɢɯ ɡɚɞɚɱɚɯ ɧɨɪɦɚɥɶɧɿɫɬɶ ɪɟɡɭɥɶɬɚɬɿɜ ɜɢɩɪɨ-

ɛɭɜɚɧɶ ɜɫɬɚɧɨɜɢɬɢ ɿɡ ɡɚɝɚɥɶɧɢɯ ɦɿɪɤɭɜɚɧɶ, ɹɤ ɩɪɚɜɢɥɨ, ɧɟ ɦɨɠɥɢɜɨ. ɇɨɪɦɚ-

ɥɶɧɿɫɬɶ ɜɚɪɬɨ ɩɟɪɟɜɿɪɹɬɢ ɡɚ ɞɨɩɨɦɨɝɨɸ ɫɬɚɬɢɫɬɢɱɧɢɯ ɤɪɢɬɟɪɿʀɜ, ɚɛɨ ɠ ɜɢɤɨ-

ɪɢɫɬɨɜɭɜɚɬɢ ɧɟɩɚɪɚɦɟɬɪɢɱɧɿ ɦɟɬɨɞɢ (ɞɢɜ. ɪɨɡɞɿɥ 5.3).

Ɋɨɡɩɨɞɿɥɢ «ɯɿ-ɤɜɚɞɪɚɬ», ɋɬɶɸɞɟɧɬɚ ɿ Ɏɿɲɟɪɚ

ɉɪɢ ɩɨɛɭɞɨɜɿ ɫɬɚɬɢɫɬɢɱɧɢɯ ɦɨɞɟɥɟɣ ɧɨɪɦɚɥɶɧɨɦɭ ɡɚɤɨɧɨɜɿ ɛɟɡɭɦɨɜɧɨ

ɧɚɥɟɠɢɬɶ ɰɟɧɬɪɚɥɶɧɟ ɦɿɫɰɟ. ɉɪɨɬɟ ɧɚɦɚɝɚɧɧɹ ɜɢɤɨɪɢɫɬɨɜɭɜɚɬɢ ɣɨɝɨ ɞɥɹ ɦɨ-

ɞɟɥɸɜɚɧɧɹ ɪɨɡɩɨɞɿɥɭ ɟɦɩɿɪɢɱɧɢɯ ɞɚɧɢɯ ɭ ɛɭɞɶ-ɹɤɨɦɭ ɪɚɡɿ ɧɟ ɡɚɜɠɞɢ ɽ ɨɛʉɪɭ-

ɧɬɨɜɚɧɢɦɢ. Ȼɿɥɶɲ ɿɫɬɨɬɧɨ ɬɟ, ɳɨ ɛɚɝɚɬɨ ɦɟɬɨɞɿɜ ɨɛɪɨɛɤɢ ɞɚɧɢɯ ɡɚɫɧɨɜɚɧɨ ɧɚ

ɪɨɡɪɚɯɭɧɤɨɜɢɯ ɜɟɥɢɱɢɧɚɯ, ɳɨ ɦɚɸɬɶ ɯɨɱɚ ɣ ɿɧɲɿ, ɚɥɟ ɛɥɢɡɶɤɿ ɪɨɡɩɨɞɿɥɢ ɞɨ

ɪɨɡɩɨɞɿɥɭ

ɧɨɪɦɚɥɶɧɨɝɨ. Ʉɪɿɦ ɬɨɝɨ, ɡɚ ɞɨɩɨɦɨɝɨɸ ɧɨɪɦɚɥɶɧɨɝɨ ɡɚɤɨɧɭ ɜɢɡɧɚ-

ɱɚɸɬɶɫɹ ɲɢɪɨɤɨ ɪɨɡɩɨɜɫɸɞɠɟɧɿ ɜ ɦɚɬɟɦɚɬɢɱɧɿɣ ɫɬɚɬɢɫɬɢɰɿ ɪɨɡɩɨɞɿɥɢ

(ɯɿ-

ɤɜɚɞɪɚɬ

), t ɋɬɶɸɞɟɧɬɚ ɿ F Ɏɿɲɟɪɚ.

143

Ɋɨɡɩɨɞɿɥ Ȥ

(ɯɿ-ɤɜɚɞɪɚɬ) – ɰɟ ɪɨɡɩɨɞɿɥ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ

X = X

+ X

+ ... + X

, (3.61)

ɞɟ ɜɢɩɚɞɤɨɜɿ ɜɟɥɢɱɢɧɢ

, X

, ..., X

ɽ ɧɟɡɚɥɟɠɧɢɦɢ ɿ ɦɚɸɬɶ ɬɨɣ ɫɚɦɢɣ ɫɬɚ-

ɧɞɚɪɬɧɢɣ ɧɨɪɦɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ

N(0,1). Ʉɿɥɶɤɿɫɬɶ ɞɨɞɚɧɤɿɜ n ɧɚɡɢɜɚɽɬɶɫɹ «ɱɢ-

ɫɥɨɦ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ» ɪɨɡɩɨɞɿɥɭ ɯɿ-ɤɜɚɞɪɚɬ.

Ɋɨɡɩɨɞɿɥ t ɋɬɶɸɞɟɧɬɚ – ɰɟ ɪɨɡɩɨɞɿɥ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ

, (3.62)

ɞɟ ɜɢɩɚɞɤɨɜɿ ɜɟɥɢɱɢɧɢ

U ɿ X ɧɟɡɚɥɟɠɧɿ, U ɦɚɽ ɫɬɚɧɞɚɪɬɧɢɣ ɧɨɪɦɚɥɶɧɢɣ

ɪɨɡɩɨɞɿɥ

N(0,1), ɚ X – ɪɨɡɩɨɞɿɥ ɯɿ-ɤɜɚɞɪɚɬ ɡ n ɫɬɭɩɟɧɹɦɢ ɜɿɥɶɧɨɫɬɿ. ɉɪɢ ɰɶɨɦɭ

n ɧɚɡɢɜɚɽɬɶɫɹ «ɱɢɫɥɨɦ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ» ɪɨɡɩɨɞɿɥɭ ɋɬɶɸɞɟɧɬɚ.

Ɋɨɡɩɨɞɿɥ F Ɏɢɲɟɪɚ – ɰɟ ɪɨɡɩɨɞɿɥ ɜɢɩɚɞɤɨɜɨʀ ɜɟɥɢɱɢɧɢ

F (3.63)

ɞɟ ɜɢɩɚɞɤɨɜɿ ɜɟɥɢɱɢɧɢ ɏ

ɿ ɏ

– ɧɟɡɚɥɟɠɧɿ ɿ ɦɚɸɬɶ ɪɨɡɩɨɞɿɥɢ ɯɿ-ɤɜɚɞɪɚɬ ɡ

ɱɢɫɥɨɦ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ k

ɿ k

ɜɿɞɩɨɜɿɞɧɨ.

Ɉɬɠɟ, ɪɨɡɩɨɞɿɥɢ F

(ɯɿ-ɤɜɚɞɪɚɬ), t ɋɬɶɸɞɟɧɬɚ ɿ F Ɏɿɲɟɪɚ ɽ ɩɨɯɿɞɧɢɦɢ ɜɿɞ

ɧɨɪɦɚɥɶɧɨɝɨ ɡɚɤɨɧɭ. Ɋɨɡɝɥɹɧɟɦɨ ɜɥɚɫɬɢɜɨɫɬɿ ɰɢɯ ɪɨɡɩɨɞɿɥɿɜ ɞɨɤɥɚɞɧɿɲɟ.

Ɋɨɡɩɨɞɿɥ Ȥ

«ɯɿ-ɤɜɚɞɪɚɬ» ɦɨɠɧɚ ɨɬɪɢɦɚɬɢ ɡɚ ɫɯɟɦɨɸ ɩɨɜɬɨɪɧɢɯ ɜɢɩɪɨɛɭ-

ɜɚɧɶ, ɹɤɳɨ ɡ ɝɟɧɟɪɚɥɶɧɨʀ ɫɭɤɭɩɧɨɫɬɿ ɧɨɪɦɚɥɶɧɨ ɪɨɡɩɨɞɿɥɟɧɢɯ ɡɧɚɱɟɧɶ ɡ ɧɭ-

ɥɶɨɜɢɦ ɫɟɪɟɞɧɿɦ (ȝ=0) ɿ ɨɞɢɧɢɱɧɢɦ ɫɬɚɧɞɚɪɬɧɢɦ ɜɿɞɯɢɥɟɧɧɹɦ (ı=1) ɜɢɩɚɞɤɨ-

ɜɢɦ ɦɟɬɨɞɨɦ ɜɢɥɭɱɚɬɢ ɧɟɡɚɥɟɠɧɨ n ɡɧɚɱɟɧɶ X

, X

, ..., X

, ɚ ɩɨɬɿɦ ɪɨɡɪɚɯɨɜɭ-

ɜɚɬɢ ɫɭɦɭ ʀɯ ɤɜɚɞɪɚɬɿɜ (X

)

+ (X

)

+ …+ (X

)

. ɍ ɪɟɡɭɥɶɬɚɬɿ ɛɚɝɚɬɨɪɚɡɨɜɢɯ ɜɢ-

ɩɪɨɛɭɜɚɧɶ ɡɧɚɱɟɧɧɹ ɰɢɯ ɫɭɦ ɛɭɞɭɬɶ ɦɚɬɢ ɪɨɡɩɨɞɿɥ Ȥ

(ɯɿ-ɤɜɚɞɪɚɬ) ɡ n ɫɬɟɩɟ-

ɧɹɦɢ ɜɿɥɶɧɨɫɬɿ. Ⱥɧɚɥɿɬɢɱɧɚ ɮɨɪɦɚ ɡɚɩɢɫɭ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ Ȥ

ɦɚɽ ɜɢɝɥɹɞ:

),(

nxf





*

, (3.64)

ɞɟ f

Ȥ2

(x, n) – ɮɭɧɤɰɿɹ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ Ȥ

; n – ɱɢɫɥɨ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫ-

144

ɬɿ; ī() – ɝɚɦɚ-ɮɭɧɤɰɿɹ, ɹɤɚ ɡɪɭɱɧɨ ɪɨɡɪɚɯɨɜɭɽɬɶɫɹ ɜ Excel ɡɚ ɞɨɩɨɦɨɝɨɸ ɜɢɪɚ-

ɡɭ =EXP(ȽȺɆɆȺɇɅɈȽ()). Ɏɭɧɤɰɿɹ f

Ȥ2

(x, n)>0 ɞɥɹ x  0 ɿ f

Ȥ2

(x, n)=0 ɞɥɹ x<0.

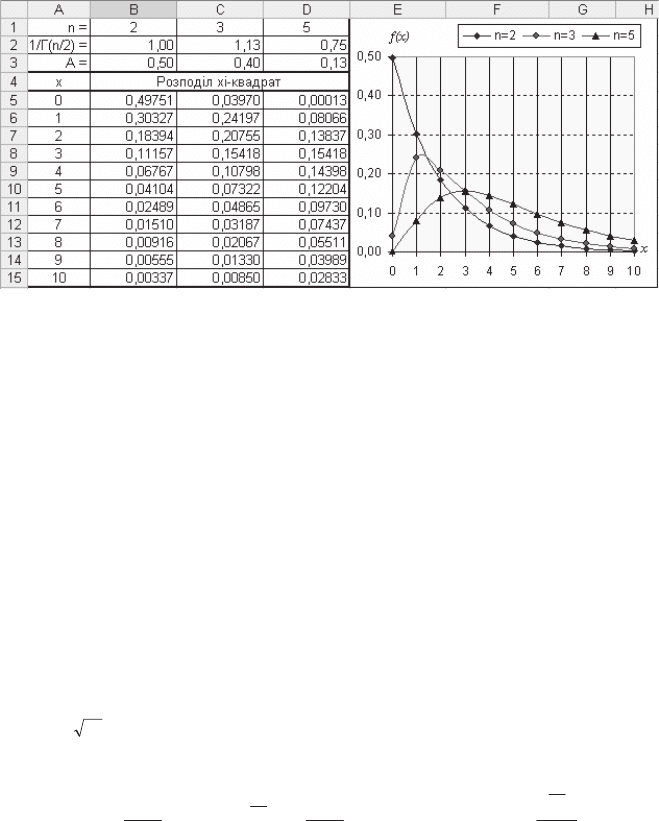
ɇɚ ɪɢɫ. 3.49. ɩɨɤɚɡɚɧɨ ɪɨɡɪɚɯɭɧɤɢ ɡɧɚɱɟɧɶ ɿ ɝɪɚɮɿɤɢ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ

ɞɥɹ ɬɪɶɨɯ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ (2; 3 ɿ 5).

Ɋɢɫ. 3.49. Ɋɨɡɪɚɯɭɧɤɢ ɿ ɝɪɚɮɿɤɢ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ Ȥ

Ⱦɥɹ ɪɨɡɪɚɯɭɧɤɭ ɪɨɡɩɨɞɿɥɭ Ȥ

ɡ ɱɢɫɥɨɦ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ, ɧɚɩɪɢɤɥɚɞ, n=2

ɧɟɨɛɯɿɞɧɨ ɜɧɟɫɬɢ:

ɭ ɤɨɦɿɪɤɭ ȼ2 ɜɢɪɚɡ =1/EXP(ȽȺɆɆȺɇɅɈȽ(B$1/2));

ɭ ɤɨɦɿɪɤɭ ȼ3 ɜɢɪɚɡ =B2/2^(B$1/2);

ɭ ɤɨɦɿɪɤɭ ȼ5 ɜɢɪɚɡ =B$3*$A5^(B$1/2-1)*EXP(-$A5/2);

ɭ ɤɨɦɿɪɤɢ ȼ6:ȼ15 – ɚɧɚɥɨɝɿɱɧɿ ɜɢɪɚɡɢ.

ɍ ɫɬɨɜɩɱɢɤɚɯ ɋ ɿ D ɪɨɡɪɚɯɨɜɚɧɨ ɡɧɚɱɟɧɧɹ ɪɨɡɩɨɞɿɥɭ Ȥ

ɞɥɹ ɱɢɫɥɚ ɫɬɭɩɟɧɿɜ

ɜɿɥɶɧɨɫɬɿ n=3 ɿ n=5.

əɤ ɜɢɞɧɨ ɡ ɝɪɚɮɿɤɿɜ, ɩɪɢ ɡɛɿɥɶɲɟɧɧɿ ɱɢɫɥɚ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ n ɪɨɡɩɨɞɿɥ Ȥ

ɧɚɛɥɢɠɚɽɬɶɫɹ ɞɨ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ ɡ ɫɟɪɟɞɧɿɦ n ɿ ɫɬɚɧɞɚɪɬɧɢɦ ɜɿɞɯɢ-

ɥɟɧɧɹɦ

. əɤɳɨ ɞɢɫɩɟɪɫɿɸ ɦɨɠɧɚ ɡɚɩɢɫɚɬɢ ɹɤ ɫɭɦɭ ɤɜɚɞɪɚɬɿɜ n ɧɟɡɚɥɟɠ-

ɧɢɯ ɜɢɩɚɞɤɨɜɢɯ ɡɧɚɱɟɧɶ ɜɢɩɪɨɛɭɜɚɧɶ X

, X

, ..., X

, ɧɚɩɪɢɤɥɚɞ,

)(







XXX

XnX

ɬɨ ɜɟɥɢɱɢɧɚ s

ɦɨɠɟ ɦɚɬɢ ɪɨɡɩɨɞɿɥ Ȥ

. Ɍɨɦɭ ɩɪɢɪɨɞɧɨ, ɳɨ ɪɨɡɩɨɞɿɥɢ Ȥ

ɜɢ-

145

ɤɨɪɢɫɬɨɜɭɸɬɶ ɭ ɫɬɚɬɢɫɬɢɱɧɢɯ ɜɢɫɧɨɜɤɚɯ ɳɨɞɨ ɞɢɫɩɟɪɫɿɣ (ɞɢɜ. ɪɨɡɞɿɥ 5.4) .

Ɋɨɡɩɨɞɿɥ t ɋɬɶɸɞɟɧɬɚ. ȼɥɚɫɬɢɜɨɫɬɿ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ ɦɨɠɧɚ ɜɢɤɨ-

ɪɢɫɬɨɜɭɜɚɬɢ ɥɢɲɟ ɬɨɞɿ, ɤɨɥɢ ɨɛɫɹɝ ɜɢɛɿɪɤɢ n ɽ «ɞɨɫɬɚɬɧɶɨ ɜɟɥɢɤɢɦ» – ɧɚ ɰɟ

ɡɜɟɪɬɚɽ ɭɜɚɝɭ ɰɟɧɬɪɚɥɶɧɚ ɝɪɚɧɢɱɧɚ ɬɟɨɪɟɦɚ. ɉɪɨɬɟ ɜ ɪɟɚɥɶɧɢɯ ɭɦɨɜɚɯ ɨɛɫɹɝ

ɜɢɛɿɪɤɢ, ɹɤ ɩɪɚɜɢɥɨ, ɧɟ ɽ «ɞɨɫɬɚɬɧɶɨ ɜɟɥɢɤɢɦ». ɍ ɰɢɯ ɭɦɨɜɚɯ ɜɢɤɨɪɢɫɬɨɜɭɸɬɶ

ɿɧɲɿ ɪɨɡɩɨɞɿɥɢ. Ɉɞɧɢɦ ɿɡ ɧɚɣɜɚɠɥɢɜɿɲɢɯ ɜɜɚɠɚɽɬɶɫɹ ɪɨɡɩɨɞɿɥ ɋɬɶɸɞɟɧɬɚ:

),(







*



nxf

, (3.65)

ɞɟ f

(x, n) – ɮɭɧɤɰɿɹ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ ɋɬɶɸɞɟɧɬɚ; n – ɱɢɫɥɨ ɫɬɭɩɟɧɿɜ

ɜɿɥɶɧɨɫɬɿ; ī() – ɝɚɦɚ-ɮɭɧɤɰɿɹ.

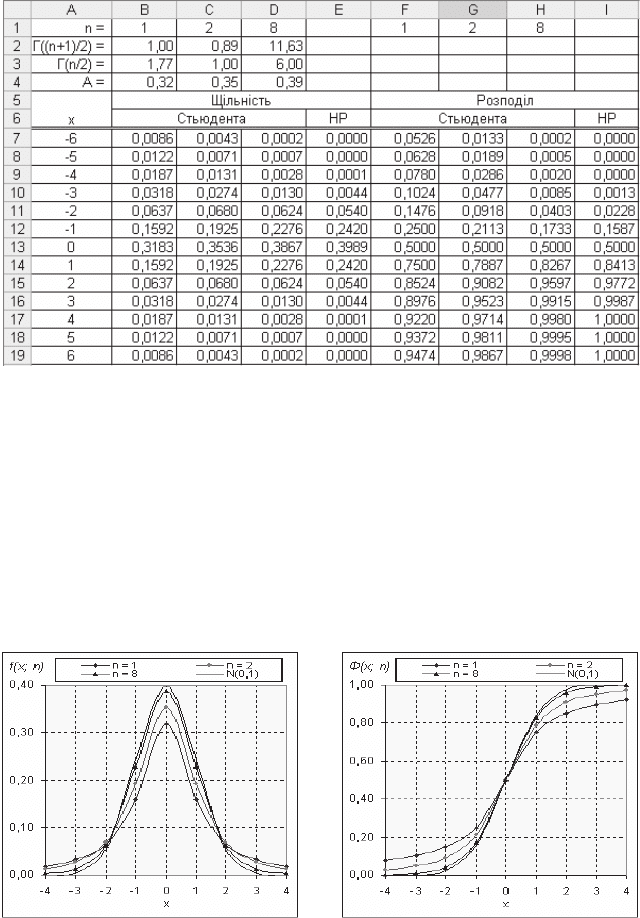
ɇɚ ɪɢɫ. 3.50. ɩɨɤɚɡɚɧɨ ɪɨɡɪɚɯɭɧɤɢ ɪɨɡɩɨɞɿɥɭ ɋɬɶɸɞɟɧɬɚ ɞɥɹ ɫɬɭɩɟɧɿɜ ɜɿ-

ɥɶɧɨɫɬɿ (1; 2 ɿ 8) ɿ ɞɥɹ ɩɨɪɿɜɧɹɧɧɹ ɜɿɞɩɨɜɿɞɧɿ ɡɧɚɱɟɧɧɹ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ.

Ⱦɥɹ ɪɨɡɪɚɯɭɧɤɭ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ ɋɬɶɸɞɟɧɬɚ ɡ ɱɢɫɥɨɦ ɫɬɭɩɟɧɿɜ ɜɿɥɶ-

ɧɨɫɬɿ n=1 ɧɟɨɛɯɿɞɧɨ ɜɧɟɫɬɢ:

ɭ ɤɨɦɿɪɤɭ ȼ2 ɜɢɪɚɡ =EXP(ȽȺɆɆȺɇɅɈȽ((B$1+1)/2));

ɭ ɤɨɦɿɪɤɭ ȼ3 ɜɢɪɚɡ =EXP(ȽȺɆɆȺɇɅɈȽ(B$1/2));

ɭ ɤɨɦɿɪɤɭ ȼ4 ɜɢɪɚɡ =B2/B3/ɄɈɊȿɇɖ(B$1*ɉɂ());

ɭ ɤɨɦɿɪɤɭ ȼ7 ɜɢɪɚɡ =B$4*(1+$A7^2/B$1)^(-(B$1+1)/2);

ɭ ɤɨɦɿɪɤɢ ȼ8:ȼ19 ɜɧɟɫɬɢ ɚɧɚɥɨɝɿɱɧɿ ɜɢɪɚɡɢ;

ɍ ɫɬɨɜɩɱɢɤɚɯ ɋ ɿ D ɪɨɡɪɚɯɨɜɚɧɨ ɡɧɚɱɟɧɧɹ ɪɨɡɩɨɞɿɥɭ ɋɬɶɸɞɟɧɬɚ ɞɥɹ ɱɢɫɥɚ

ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ n=2 ɿ n=8. ɍ ɫɬɨɜɩɱɢɤɭ ȿ – ɡɧɚɱɟɧɧɹ ɳɿɥɶɧɨɫɬɿ ɧɨɪɦɚɥɶɧɨ-

ɝɨ ɪɨɡɩɨɞɿɥɭ, ɞɥɹ ɱɨɝɨ, ɧɚɩɪɢɤɥɚɞ, ɭ ɤɨɦɿɪɤɭ ȿ7 ɫɥɿɞ ɜɧɟɫɬɢ ɜɢɪɚɡ

=ɇɈɊɆɊȺɋɉ(A7;0;1;0).

Ɋɨɡɩɨɞɿɥɢ ɋɬɶɸɞɟɧɬɚ ɞɥɹ ɬɪɶɨɯ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ (1; 2 ɿ 8) ɦɨɠɧɚ ɪɨɡɪɚ-

ɯɭɜɚɬɢ

ɡɚ ɞɨɩɨɦɨɝɨɸ ɮɭɧɤɰɿʀ =ɋɌɖɘȾɊȺɋɉ(). Ɍɚɤ, ɭ ɤɨɦɿɪɤɭ F7 ɧɟɨɛɯɿɞɧɨ

ɜɧɟɫɬɢ =ɋɌɖɘȾɊȺɋɉ(ABS($A7);F$1;1), ɚɧɚɥɨɝɿɱɧɿ ɜɢɪɚɡɢ ɜɧɟɫɬɢ ɭ ɤɨɦɿɪɤɢ

F8:F13. ɍ ɤɨɦɿɪɤɭ F14 ɜɧɟɫɬɢ =1–ɋɌɖɘȾɊȺɋɉ(ABS($A14);F$1;1), ɚɧɚɥɨɝɿɱɧɿ

ɜɢɪɚɡɢ ɜɧɟɫɬɢ ɭ ɤɨɦɿɪɤɢ F15:F19. Ɍɚɤɿ ɠ ɞɿʀ ɩɪɨɜɟɫɬɢ ɭ ɫɬɨɜɩɱɢɤɚɯ G ɿ H.

146

Ɋɢɫ. 3.50. Ɂɧɚɱɟɧɧɹ ɪɨɡɩɨɞɿɥɿɜ ɋɬɶɸɞɟɧɬɚ ɿ ɪɨɡɩɨɞɿɥɭ N(0,1)

Ⱦɥɹ ɪɨɡɪɚɯɭɧɤɭ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ ɭ ɤɨɦɿɪɤɭ ȱ7 ɜɧɟɫɬɢ ɜɢɪɚɡ

=ɇɈɊɆɊȺɋɉ(A7;0;1;1), ɚɧɚɥɨɝɿɱɧɿ ɜɢɪɚɡɢ ɜɧɟɫɬɢ ɭ ɤɨɦɿɪɤɢ ȱ8:ȱ19.

ɇɚ ɪɢɫ. 3.51. ɩɨɤɚɡɚɧɨ ɫɿɦɟɣɫɬɜɨ ɝɪɚɮɿɤɿɜ ɪɨɡɩɨɞɿɥɭ ɋɬɶɸɞɟɧɬɚ ɞɥɹ ɬɪɶɨɯ ɫɬɭ-

ɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ (1; 2; 8), ɚ ɬɚɤɨɠ ɝɪɚɮɿɤ ɫɬɚɧɞɚɪɬɧɨɝɨ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ

N(0,1).

ɚ) ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ ɛ) ɪɨɡɩɨɞɿɥɢ

Ɋɢɫ. 3.51. Ƚɪɚɮɿɤɢ ɪɨɡɩɨɞɿɥɿɜ ɋɬɶɸɞɟɧɬɚ ɿ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ N(0,1)

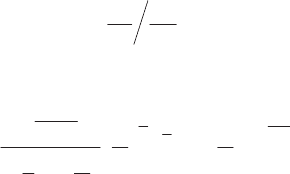
147

əɤ ɜɢɞɧɨ, ɩɪɢ ɡɛɿɥɶɲɟɧɧɿ ɱɢɫɥɚ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ n ɪɨɡɩɨɞɿɥɢ ɋɬɶɸɞɟɧɬɚ

ɚɫɢɦɩɬɨɬɢɱɧɨ ɧɚɛɥɢɠɚɸɬɶɫɹ ɞɨ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ. Ʉɨɥɢ ɨɛɫɹɝ ɜɢɛɿɪɤɢ

n ɫɬɚɽ «ɞɨɫɬɚɬɧɶɨ ɜɟɥɢɤɢɦ», ɬɨɛɬɨ ɩɪɚɤɬɢɱɧɨ

, ɪɨɡɩɨɞɿɥɢ ɋɬɶɸɞɟɧɬɚ

ɡɛɿɝɚɸɬɶɫɹ ɡ ɧɨɪɦɚɥɶɧɢɦ ɪɨɡɩɨɞɿɥɨɦ. ɇɚɣɱɚɫɬɿɲɟ ɪɨɡɩɨɞɿɥɢ

ɋɬɶɸɞɟɧɬɚ ɜɢ-

ɤɨɪɢɫɬɨɜɭɸɬɶ ɭ ɫɬɚɬɢɫɬɢɱɧɢɯ ɜɢɫɧɨɜɤɚɯ ɳɨɞɨ

ɫɟɪɟɞɧɿɯ (ɞɢɜ. ɪɨɡɞɿɥ 5.4).

Ɋɨɡɩɨɞɿɥ F Ɏɿɲɟɪɚ ɦɨɠɧɚ ɨɬɪɢɦɚɬɢ, ɜɢɤɨɪɢɫɬɨɜɭɸɱɢ ɫɯɟɦɭ ɩɨɜɬɨɪɧɢɯ

ɜɢɩɪɨɛɭɜɚɧɶ, ɤɨɥɢ ɡ ɝɟɧɟɪɚɥɶɧɨʀ ɫɭɤɭɩɧɨɫɬɿ ɧɨɪɦɚɥɶɧɨ ɪɨɡɩɨɞɿɥɟɧɢɯ ɡɧɚɱɟɧɶ

ɡ ɩɚɪɚɦɟɬɪɚɦɢ (

ȝ=0 ɿ ı=1) ɜɢɩɚɞɤɨɜɢɦ ɦɟɬɨɞɨɦ ɫɩɨɱɚɬɤɭ ɮɨɪɦɭɸɬɶ ɩɟɪɲɭ

ɡɦɿɧɧɭ

ɡ ɪɨɡɩɨɞɿɥɨɦ «ɯɿ-ɤɜɚɞɪɚɬ» ɿ ɫɬɟɩɟɧɹɦɢ ɜɿɥɶɧɨɫɬɿ n, ɚ ɩɨɬɿɦ ɧɟɡɚɥɟɠ-

ɧɢɦ ɲɥɹɯɨɦ ɮɨɪɦɭɸɬɶ ɞɪɭɝɭ ɡɦɿɧɧɭ

ɡ ɪɨɡɩɨɞɿɥɨɦ «ɯɿ-ɤɜɚɞɪɚɬ» ɿ ɫɬɟɩɟɧɹ-

ɦɢ ɜɿɥɶɧɨɫɬɿ

m. ɇɨɜɚ ɜɢɩɚɞɤɨɜɚ ɜɟɥɢɱɢɧɚ, ɳɨ ɦɚɽ ɜɥɚɫɬɢɜɨɫɬɿ ɪɨɡɩɨɞɿɥɭ Ɏɿ-

ɲɟɪɚ, ɫɤɥɚɞɚɬɢɦɟɬɶɫɹ ɡ ɜɿɞɧɨɲɟɧɧɹ

. (3.66)

Ɏɭɧɤɰɿɹ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ Ɏɿɲɟɪɚ ɦɚɽ ɜɢɝɥɹɞ

),,(

mnxf







*



, (3.67)

ɞɟ

(x, n, m) – ɮɭɧɤɰɿɹ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ Ɏɿɲɟɪɚ; n ɿ m – ɱɢɫɥɨ ɫɬɭɩɟ-

ɧɿɜ ɜɿɥɶɧɨɫɬɿ; ī() – ɝɚɦɚ-ɮɭɧɤɰɿɹ.

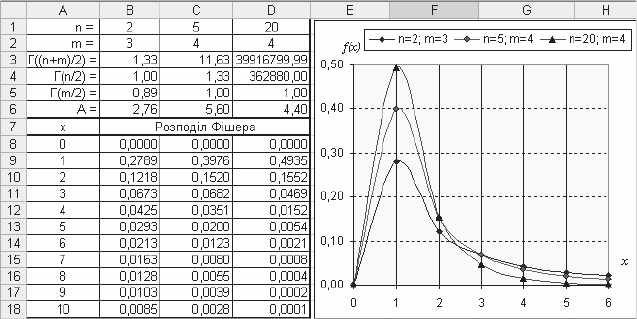
ɇɚ ɪɢɫ. 3.52. ɩɨɤɚɡɚɧɨ ɪɨɡɪɚɯɭɧɤɢ ɿ ɝɪɚɮɿɤɢ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ Ɏɿɲɟɪɚ

ɞɥɹ ɬɪɶɨɯ ɧɚɛɨɪɿɜ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ n ɿ m (2 ɿ 3; 5 ɿ 4; 20 ɿ 4 ɜɿɞɩɨɜɿɞɧɨ).

Ⱦɥɹ ɪɨɡɪɚɯɭɧɤɭ ɪɨɡɩɨɞɿɥɭ Ɏɿɲɟɪɚ, ɧɚɩɪɢɤɥɚɞ,

ɡ ɱɢɫɥɨɦ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫ-

ɬɿ

n=2 ɿ m=3 ɧɟɨɛɯɿɞɧɨ ɜɧɟɫɬɢ:

ɭ ɤɨɦɿɪɤɭ ȼ3 ɜɢɪɚɡ =EXP(ȽȺɆɆȺɇɅɈȽ((B$1+B$2)/2));

ɭ ɤɨɦɿɪɤɭ ȼ4 ɜɢɪɚɡ =EXP(ȽȺɆɆȺɇɅɈȽ(B$1/2));

ɭ ɤɨɦɿɪɤɭ ȼ5 ɜɢɪɚɡ =EXP(ȽȺɆɆȺɇɅɈȽ(B$2/2));

ɭ ɤɨɦɿɪɤɭ ȼ6 ɜɢɪɚɡ =B3/B4/B5*(B$2/B$1)^(B$2/2);

ɭ ɤɨɦɿɪɤɭ ȼ7 ɜɢɪɚɡ =B$6*$A8^(B$2/2-1)*(1+B$2/B$1*$A8)^(-(B$2+B$1)/2);

148

x ɭ ɤɨɦɿɪɤɢ ȼ8:ȼ18 – ɚɧɚɥɨɝɿɱɧɿ ȼ7 ɜɢɪɚɡɢ.

Ɋɢɫ. 3.52. Ɂɧɚɱɟɧɧɹ ɿ ɝɪɚɮɿɤɢ ɳɿɥɶɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ Ɏɿɲɟɪɚ

ɍ ɫɬɨɜɩɱɢɤɚɯ ɋ ɿ D ɪɨɡɪɚɯɨɜɚɧɨ ɡɧɚɱɟɧɧɹ ɪɨɡɩɨɞɿɥɭ Ɏɿɲɟɪɚ

ɞɥɹ ɿɧɲɢɯ

ɧɚɛɨɪɿɜ ɱɢɫɥɚ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ

n ɿ m. Ɂ ɪɢɫ. 3.52. ɜɢɞɧɨ, ɳɨ ɩɪɢ ɡɛɿɥɶɲɟɧɧɿ

ɱɢɫɥɚ ɫɬɭɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ

n ɿ m ɪɨɡɩɨɞɿɥ Ɏɿɲɟɪɚ

ɧɚɛɥɢɠɚɽɬɶɫɹ ɞɨ ɧɨɪɦɚɥɶɧɨɝɨ

ɪɨɡɩɨɞɿɥɭ ɡ ɫɟɪɟɞɧɿɦ

m/(n–2). Ɏɭɧɤɰɿɹ f

(x, n, m)>0 ɞɥɹ x0 ɿ f

(x, n, m) = 0

ɞɥɹ

x <0. Ɋɨɡɩɨɞɿɥ Ɏɿɲɟɪɚ ɽ ɬɟɨɪɟɬɢɱɧɨɸ ɛɚɡɨɸ ɞɢɫɩɟɪɫɿɣɧɨɝɨ ɚɧɚɥɿɡɭ, ɳɨ

ɛɚɡɭɽɬɶɫɹ ɧɚ ɡɿɫɬɚɜɥɟɧɧɿ ɞɢɫɩɟɪɫɿɣ ɜɢɛɿɪɨɤ ɜɢɩɚɞɤɨɜɨ ɜɢɬɹɝɧɭɬɢɯ ɿɡ ɧɨɪɦɚɥɶ-

ɧɨʀ ɫɭɤɭɩɧɨɫɬɿ, ɜɿɞɧɨɲɟɧɧɹ ɹɤɢɯ ɫɤɥɚɞɚɽ

F-ɤɪɢɬɟɪɿɣ Ɏɿɲɟɪɚ: F=s

, ɞɟ s

– ɞɢɫɩɟɪɫɿʀ ɩɟɪɲɨʀ ɿ ɞɪɭɝɨʀ ɜɢɛɿɪɨɤ (ɞɢɜ. ɪɨɡɞɿɥ 5.4).

Ⱦɥɹ ɩɨɪɿɜɧɹɧɧɹ ɜɥɚɫɬɢɜɨɫɬɟɣ ɪɨɡɩɨɞɿɥɿɜ «ɯɿ-ɤɜɚɞɪɚɬ», ɋɬɶɸɞɟɧɬɚ ɿ Ɏɿɲɟ-

ɪɚ ʀɯɧɿ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɩɪɟɞɫɬɚɜɥɟɧɨ ɜ ɬɚɛɥ. 3.8.

ɇɚ ɜɥɚɫɬɢɜɨɫɬɹɯ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ, ɪɨɡɩɨɞɿɥɿɜ ɋɬɶɸɞɟɧɬɚ, Ɏɿɲɟɪɚ

ɯɿ-ɤɜɚɞɪɚɬ ɩɨɛɭɞɨɜɚɧɨ ɦɚɬɟɦɚɬɢɱɧɿ ɦɟɬɨɞɢ ɫɬɚɬɢɫɬɢɱɧɨɝɨ ɨɰɿɧɸɜɚɧɧɹ, ɩɟɪɟ-

ɜɿɪɤɢ ɫɬɚɬɢɫɬɢɱɧɢɯ ɝɿɩɨɬɟɡ, ɞɢɫɩɟɪɫɿɣɧɢɣ ɚɧɚɥɿɡ ɬɚ ɿɧ. (ɞɢɜ. ɪɨɡɞɿɥɢ 5 ɿ 6).

Ɍɚɛɥɢɰɿ ɡɧɚɱɟɧɶ ɰɢɯ

ɪɨɡɩɨɞɿɥɿɜ ɦɨɠɧɚ ɡɧɚɣɬɢ ɜ ɫɩɟɰɿɚɥɶɧɿɣ ɥɿɬɟɪɚɬɭɪɿ ɚɛɨ

ɫɤɨɪɢɫɬɚɬɢɫɹ ɜɿɞɩɨɜɿɞɧɢɦɢ ɮɭɧɤɰɿɹɦɢ MS Excel, ɡɨɤɪɟɦɚ: =ɇɈɊɆɊȺɋɉ(),

=ɇɈɊɆɋɌɊȺɋɉ(), =ɏɂ2ɊȺɋɉ(), =ɋɌɖɘȾɊȺɋɉ(), =FɊȺɋɉ().

149

Ɍɚɛɥɢɰɹ 3.8

ɏɚɪɚɤɬɟɪɢɫɬɢɤɢ ɪɨɡɩɨɞɿɥɿɜ

Ɋɨɡɩɨɞɿɥɢ

ɉɚɪɚɦɟɬɪɢ

ɋɬɶɸɞɟɧɬɚ

t(x;n)

ɏɿ-ɤɜɚɞɪɚɬ Ȥ

(x;n)

Ɏɿɲɟɪɚ

F(x;n,m)

ɓɿɥɶɧɿɫɬɶ

ɪɨɡɩɨɞɿɥɭ







*







*







*



Ɇɚɬɟɦɚ-

ɬɢɱɧɟ ɫɩɨɞɿ-

ɜɚɧɧɹ

M[(n)] = 0

M[Ȥ

(n)] = n

] m)[F(n, M



ɩɪɢ n>2

Ⱦɢɫɩɟɪɫɿɹ

] t(n)D[



ɩɪɢ n>2

D [Ȥ

(n)] = 2n

)4(2)n(m

)2(2m

] m)[F(n, D





ɩɪɢ m>4

ɋɬɚɧɞ.

ɜɿɞɯɢɥɟɧɧɹ.

[t(n)]



ɩɪɢ n>2

2n (n)][

)4(2)(m

)2(2m

m)][F(n,





ɩɪɢ m>4

Ⱥɫɢɦɟɬɪɿɹ

= 0

)2(6)(m

)4(82)m(2n





mnn

ɩɪɢ m>6

ȿɤɫɰɟɫ



ɩɪɢ n>4

)5.02)(6(3





ɩɪɢ n>8

Ɂɚɩɢɬɚɧɧɹ. Ɂɚɜɞɚɧɧɹ.

1. ɉɪɨ ɳɨ ɫɬɜɟɪɞɠɭɽ ɬɟɨɪɟɦɚ Ȼɟɪɧɭɥɥɿ?

2. ɉɪɢ ɹɤɢɯ ɭɦɨɜɚɯ «ɩɪɚɰɸɽ» ɛɿɧɨɦɿɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ?

3. əɤɢɣ ɜɢɝɥɹɞ ɦɚɸɬɶ ɝɪɚɮɿɤɢ ɞɢɮɟɪɟɧɰɿɚɥɶɧɨɝɨ ɬɚ ɿɧɬɟɝɪɚɥɶɧɨɝɨ ɛɿɧɨ-

ɦɿɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ?

əɤɚ ɨɫɧɨɜɧɚ ɿɞɟɹ ɡɚɝɚɥɶɧɨʀ ɦɟɬɨɞɢɤɢ ɜɢɤɨɪɢɫɬɚɧɧɹ ɬɟɨɪɟɬɢɱɧɢɯ ɮɭɧ-

ɤɰɿɣ ɧɚ ɩɪɢɤɥɚɞɿ ɛɿɧɨɦɿɚɥɶɧɨɝɨ

ɪɨɡɩɨɞɿɥɭ ɜ ɪɿɲɟɧɧɿ ɪɟɚɥɶɧɢɯ ɡɚɜɞɚɧɶ?

Ɋɨɡɤɪɢɣɬɟ ɨɫɨɛɥɢɜɨɫɬɿ ɮɭɧɤɰɿɣ ɳɿɥɶɧɨɫɬɿ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ ɿ

ɮɭɧɤɰɿʀ ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ.

150

6. Ɉɯɚɪɚɤɬɟɪɢɡɭɣɬɟ ɫɬɚɧɞɚɪɬɧɢɣ ɧɨɪɦɚɥɶɧɢɣ ɪɨɡɩɨɞɿɥ.

7. ɑɢɦ ɜɿɞɪɿɡɧɹɸɬɶɫɹ ɪɨɡɩɨɞɿɥɢ ɋɬɶɸɞɟɧɬɚ, Ɏɿɲɟɪɚ ɿ «ɯɿ-ɤɜɚɞɪɚɬ» ɜɿɞ

ɧɨɪɦɚɥɶɧɨɝɨ ɪɨɡɩɨɞɿɥɭ?

ɉɨɜɬɨɪɿɬɶ ɦɚɬɟɦɚɬɢɱɧɿ ɩɪɨɰɟɞɭɪɢ ɡɚɜɞɚɧɶ ɡɚ ɩɪɢɤɥɚɞɨɦ 3.19.

ȼɢɤɨɧɚɣɬɟ ɥɚɛɨɪɚɬɨɪɧɭ ɪɨɛɨɬɭ ʋ 8.