Романов В.Н. Теория измерений. Основы теории точности средств измерений

Подождите немного. Документ загружается.

Гамма-распределение. Это распределение является

непрерывным и используется для описания случайных величин,

ограниченных с одной стороны. Его плотность имеет вид

() ; 0; 0; 0,5

()

fx e x b c

bc b

−

⎛⎞

⎜⎟

⎝⎠

−

=≥>≥

, (4.13)

где

а – параметр сдвига, b – параметр масштаба, с – параметр

формы, Г(

с) – известная гамма-функция. Если с – положительное

целое число, то Г(

с)=(с-1)!. Обычно полагают при расчетах а=0, а

вместо

b используют другой параметр λ=b⎯¹. При изменении

параметра

λ форма распределения не меняется, а меняется

только масштаб. В частности, при

с<1 плотность распределения

имеет вид убывающей функции, а при с>1 представляет собой

одновершинную кривую с максимумом в точке

х=(с-1)/λ. Гамма-

распределение описывает время, необходимое для появления

ровно

c независимых событий (например, отказов), если они

происходят с постоянной интенсивностью. Гамма-распределение

играет важную роль в теории массового обслуживания, где

рассматриваются задачи, связанные с ожиданием в очереди.

Если, например, заявки на контроль и ремонт СИ поступают с

постоянной интенсивностью (

λ единиц в месяц) независимо друг

от друга, а контроль и ремонт СИ производится партиями

объемом

c, то время, за которое будут проверены все приборы

является случайной величиной, подчиняющейся гамма-

распределению. Его широкое использование объясняется тем, что

гамма-распределение принимает самые разнообразные формы.

Частными случаями этого распределения являются

распределения: Эрланга, когда параметр

с – натуральное число;

"хи-квадрат", когда параметр

λ=0,5 и с кратно 0,5;

экспоненциальное, когда параметр

с=1. Часто гамма-

распределение используется в альтернативной форме:

() ,0

()

fy y e p

−−

=<<∞

, (4.14)

где

p – параметр формы и введена новая переменная y=(x–a)/b.

Математическое ожидание в этом случае равно:

M[y]=p;

дисперсия равна математическому ожиданию, т.е.

D[y]=p.

Вопросы, изложенные в данном разделе, рассмотрены,

например, в [22, 35, 45].

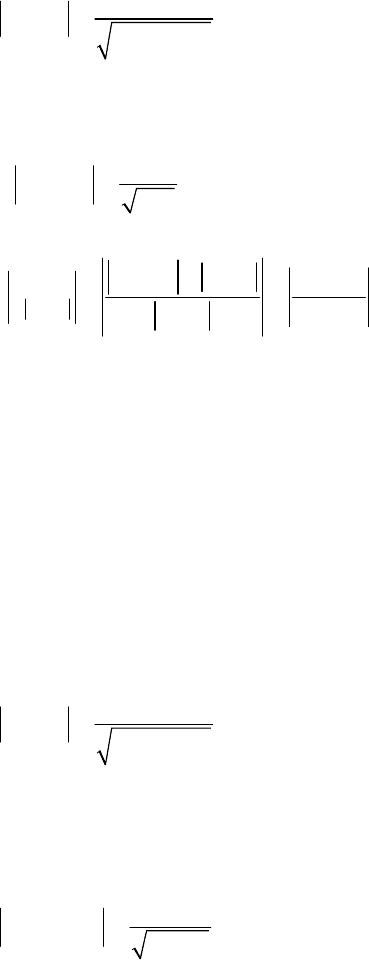
5. Примеры решения задач

Задача 1.

Фильтр нижних частот (ФНЧ) имеет следующие параметры: R

=200 кОм, C =0,4 мкФ. Требуется определить погрешность

фильтра по амплитуде на граничной частоте

ω=ω

Решение.

Амплитудно-частотная характеристика (АЧХ) фильтра дается

выражением (3.33) [42]:

()

Определим граничную частоту

. Подставляя исходные

данные, найдем

=12,5 Гц. Значение АЧХ на этой частоте равно:

0, 71

()

Относительная погрешность ФНЧ равна:

()

() (0)

0, 71 1

0,29 29%

(0) 1

−

====

Погрешность фильтра понимается здесь как уменьшение

амплитуды сигнала на выходе по сравнению с сигналом на входе.

Задача 2.

Фильтр верхних частот (ФВЧ) имеет следующие параметры: R

=50 кОм, C =0,1 мкФ. Требуется определить погрешность

фильтра по амплитуде на частоте

ω=10ω

Решение.

АЧХ ФВЧ дается выражением (3.40) [42]:

()

Определим граничную частоту

. Подставляя исходные

данные, найдем

=200 Гц. Значение АЧХ на частоте ω=10ω

равно:

0,995

110

(10 )

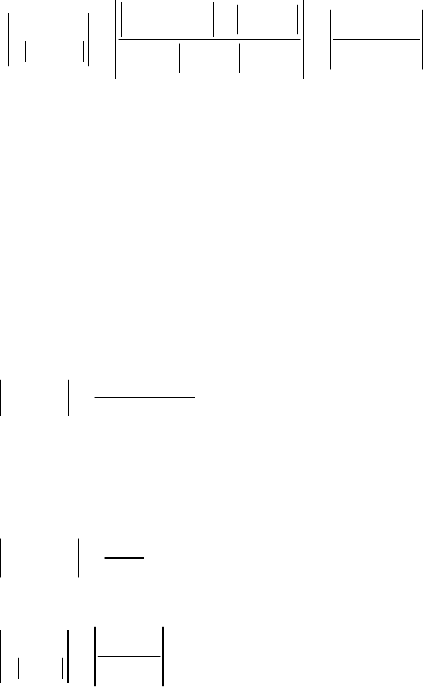
Относительная погрешность ФВЧ равна:

(10 )

(10 ) ( )

0,995 1

0,005 0,5%

() 1

−∞

−

====

∞

Задача 3.

Полосовой фильтр (ПФ) имеет следующие параметры: R

= R

=100 кОм, C

= C

=0,2 мкФ. Требуется определить погрешность

фильтра по амплитуде на частоте

Решение.

АЧХ ПФ дается выражением (3.44) [42]:

()

Определим граничную частоту

. Подставляя исходные

данные, найдем

=50 Гц. Значение АЧХ на частоте ω

равно:

0,5

()

Относительная погрешность ПФ равна:

()

0,5 1

0,5 50%

−

===

Задача 4.

Определите предельную точность осциллографа при

температуре 40

C, если его входное сопротивление 200 МОм,

полоса частот 10 МГц.

Решение.

Точность осциллографа ограничена тепловым шумом. Для

определения эффективного напряжения теплового шума

используем формулу Найквиста (2.3.13):

R эфф

UkTR

=Δ

Подставляя исходные данные, найдем:

22322666

3,1310 210 10 1010 351041,3810

R эфф

−−

⋅⋅⋅⋅⋅⋅⋅=⋅=⋅ ⋅

610

R эфф

−

≅⋅

Задача 5.

Определите предельную точность вакуумного диода при

температуре 20

C, если величина тока 10 мА, полоса частот 100

кГц.

Решение.

Точность диода ограничена дробовым эффектом. Для

определения эффективного эффективного шумового тока

используем уравнение Шотки (2.3.35):

S эфф

Δ= .

Подставляя исходные данные, найдем:

21932316

20 10 2 10 10 12,8 1021,610

S эфф

−− −

⋅⋅ ⋅⋅ ⋅ = ⋅=⋅ ⋅ ,

3, 6 10

S эфф

−

≅⋅ .

Задача 6.

Определите число фотонов, которое в среднем должен

зарегистрировать фотодиод на длине волны 400 нм в полосе

частот 100 кГц за время 10 мс.

Решение.

Значение числа фотонов ограничено квантовым шумом

приемника. Для определения числа фотонов используем ф.(2.3.45)

для эквивалентной мощности шума на детекторе:

R эфф

=Δ

Подставляя исходные данные, найдем число фотонов:

533

10 10 2 10/2 210n Pt h t

−

⋅⋅ =⋅==Δ=⋅ .

Задача 7.

Измерительное устройство состоит из 4 последовательно

соединенных элементов с функциями преобразования f

=2, f

=3,

=2, f

=3. Определите относительную погрешность сигнала на

выходе, если относительная погрешность функций

преобразования элементов составляет δf

=1%, δf

=2%, δf

=3%,

δf

=1%. Погрешность входного сигнала считать пренебрежимо

малой.

Решение.

Применим ф.(3.1.9), полагая

∑

Подставляя исходные данные, найдем

7%y

Задача 8.

Измерительное устройство состоит из 4 параллельно

соединенных элементов с функциями преобразования f

=2, f

=3,

=2, f

=3. Определите относительную погрешность сигнала на

выходе, если относительная погрешность функций

преобразования элементов составляет δf

=1%, δf

=2%, δf

=3%,

δf

=1%. Погрешность входного сигнала считать пренебрежимо

малой.

Решение.

Применим ф.(3.1.18), полагая

ii i

ff f

δδ

∑∑

Подставляя исходные данные, найдем 1, 7 %y

Задача 9.

Измерительное устройство состоит из 2-х элементов,

соединенных параллельно по схеме с отрицательной обратной

связью. Функции преобразования элементов f

=3 (прямая цепь), f

=1(обратная цепь). Определите относительную погрешность

сигнала на выходе, если относительная погрешность функций

преобразования элементов составляет δf

=4%, δf

=0,1%.

Погрешность входного сигнала считать пренебрежимо малой.

Решение.

Применим ф.(3.1.28а), полагая

112 2 2

()/

f f f signf f Q

δδ δ

=+ .

Подставляя исходные данные, найдем

1,075%y

Задача 10.

При определении скорости звука в тонком стержне из

аллюминия были получены следующие резуьлтаты: среднее

значение

5060 /v мс= , средняя ошибка 3%

(число измерений

n=5). Исследовалось также влияние на результат измерения

систематических ошибок, вызванных градиентом температуры в

образце (

), непараллельностью торцов (

) и анизотропией

образца (

). Значения границы систематической ошибки для

этих факторов составляют:

. Требуется

оценить точность результата измерения с учетом случайных и

систематических составляющих.

Решение.

Решим задачу двумя способами: используя понятие погрешности

(ошибки) и понятие неопределенности. Будем считать, что

случайные ошибки имеют нормальное распределение, а

систематические – равномерное. Доверительную вероятность

примем равной

P=0,95.

1-й способ. Для решения используем формулы теории ошибок

[42]. Доверительный интервал определяется выражением:

Δ= ⋅ , где S

– суммарная ошибка, а

t – параметр,

определяемый как среднее взвешенное случайной и

систематической, зависящий от доверительной вероятности.

Имеем следующие соотношения:

tSt S

⋅⋅

;

SSS

= ;

ktS

=⋅

∑

;

∑

;

, где m – число систематических составляющих, P –

доверительная вероятность. В нашем случае

m=3, P=0,95.

Значение коэффициента

k зависит от вероятности и

определяется приближенно. В нашем случае оно равно

1,1k =

(при

P=0,95). Значение

t определяется по таблице

распределения Стьюдента при

P=0,95 и числе степеней свободы

1n −

. В нашем случае 1 4n −= и

2,8

. Для остальных величин

расчеты дают:

2, 7%S

= ,

4, 7%

⋅

, 2, 4

, 4, 04S

= .

Доверительный интервал равен

2,4 4,04 9,7%

⋅

2-й способ. Для решения используем формулы (1.1.2 –1.1.8).

Расширенная неопределенность задается выражением:

kuu=⋅ .

Подставляя исходные данные, найдем:

4,04%

u = , 13,7

eff

= . Из таблицы распределения Стьюдента

определим коэффициент

k (при P=0,95): 2,145k = .

Неопределенность результата

8, 7%

Таким образом, оценки первым и вторым способом

получаются близкими. Расширенная неопределенность,

характеризующая точность результата, меньше на 1%, чем

доверительная ошибка. Отметим еще раз, что основное

преимущество второго подхода в более ясной схеме сложения

неопределенностей, имеющих разное происхождение. Сложение

ошибок в первом подходе основано на прближенных

полуэмпирических соотношениях, не имеющих строгого

обоснования

Литература

1. Азизов А.М., Гордов А.Н. Точность измерительных

преобразователей. – Л.: Энергия, 1975.

2. Алиев Т.М., Тер-Исраелов Г.С., Тер-Хачатуров А.А.

Вероятностные измерительно-вычислительные устройства. – М.:

Энегроатомиздат, 1983.

3.Алиев Т.М., Тер-Хачатуров А.А. Измерительные устройства:

Учебник для вузов. – М.: Высшая школа, 1991.

4. Алиев Т.М., Тер-Хачатуров А.А., Шекиханов А.М. Интерационные

методы повышения точности измерений. – М.: Энергоатомиздат, 1986.

5. Андерсон Т. Статистический анализ временных рядов. – М.:

Мир, 1976.

6. Антушев Г.С. Методы параметрического синтеза сложных

технических систем. – М.: Наука, 1989.

7. Бендат Дж., Пирсол А. Прикладной анализ случайных данных.

– М.: Мир, 1989.

8. Бендат Дж., Пирсол А. Применения корреляционного и

спектрального анализа. – М.: Мир, 1983.

9. Бокс Дж., Дженкинс Г. Анализ временных рядов. – М.: Мир,

1974.

10. Браславский Д.А., Петров В.В. Точность измерительных

устройств. – М.: Машиностроение, 1976.

11. Бромберг Э.М., Куликовский К.Л. Тестовые методы

повышения точности измерений. – М.: Энергия. 1978.

12. Ван-дер-Зил А. Шум. Источники, описание, измерение. – М.:

Сов. радио, 1973.

13. Ван Трис Г. Теория

обнаружения, оценок и модуляции. – М.:

Сов. радио, 1972.

14. Гарднер М., Бернс Дж. Переходные процессы в линейных

системах. – М.: Физматгиз, 1961.

15. Гехер К. Теория чувствительности и допусков электронных

систем. – М.: Сов. радио, 1973.

16. ГОСТ 1.25-76.ГСС. Метрологическое обеспечение. Основные

положения.

17. ГОСТ 8.009-84.ГСИ. Нормируемые метрологические

характеристики СИ.

18. Земельман М.А. Автоматическая коррекция погрешностей

измерительных

устройств. – М.: Издательство стандартов, 1972.

19. Золотова Т.М., Кербников Ф.И., Розенблат М.А.

Резервирование аналоговых устройств автоматики. – М.:

Энергоатомиздат, 1986.

20. Иванов В.В. Методы вычислений на ЭВМ. – Киев: Наукова

думка, 1986.

21. Калман Р., Фалб П., Арбиб М. Очерки по математической

теории систем. – М.: Мир, 1971.

22. Крамер Г. Методы математической статистики. – М.: Мир,

1975.

23. Кунце Х.-И

. Методы физических измерений. – М.: Мир, 1989.

24. Макшанов А.В., Мусаев А.А. Робастные методы обработки

результатов измерений: Учеб. пособие. – М.: Оборонгиз, 1980.

25. Малахов А.Н. Флуктуации в автоколебательных системах. –

М.: Радио и связь, 1968.

26. Методы электрических измерений: Учеб. пособие/Под

редакцией Э.И. Цветкова. – Л.: Энергоатомиздат, 1990.

27. МИ 2552-99. Рекомендация. ГСИ. Применение "Руководства

по выражению неопределенности измерений". – СПб.: ВНИИМ

им. Д.И. Менделеева, 1999.

28. Моисеев В.С. Системное проектирование преобразователей

информации. – Л.: Машиностроение, 1982.

29.Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия. – М.:

Финансы и статистика, 1982.

30. Мудров В.И., Кушко В.Л. Методы обработки результатов

измерений. – М.: Радио и связь, 1983.

31. Островерхов В.В. Динамические

погрешности аналого-

цифровых преобразователей. – Л.: Энергия. 1975.

32. Отнес Р., Эмоксон Л. Прикладной анализ временных рядов. -

М.: Мир, 1982.

33. Отт Г.У. Методы подавления шумов и помех в электронных

системах. – М.: Мир, 1979.

34. Петров Б.Н. Принцип инвариантности в измерительной

технике. – М.: Наука, 1976.

35. Петрович М.Л., Давидович М.И. Статистическое оценивание

проверка гипотез на ЭВМ. – М.: Финансы и статистика, 1989.

36. Пирс Дж. Символы, сигналы, шумы. Закономерности и

процессы передачи информации. – М.: Мир, 1967.

37. Рей Ф. Статистическая физика. – М.: Наука, 1986.

38. Робинсон Ф.Н.Х. Шумы и флуктуации в электронных схемах

и цепях. – М.: Атомиздат, 1980.

39. Розенберг В.Я. Введение в теорию точности измерительных

систем. – М.: Сов. радио, 1975.

40. Романов В.Н. Планирование эксперимента: Учеб. пособие. –

СПб.: СЗПИ, 1992.

41. Романов В.Н. Системный анализ для инженеров. - СПб.: СПб.

гос. университет, 1998.

42.Романов В.

Н., Комаров В.В. Анализ и обработка

экспериментальных данных: Учеб. пособие. – СПб.: СЗТУ, 2002.

43. Романов В.Н., Соболев В.С., Цветков Э.И. Интеллектуальные

средства измерений. – М.: РИЦ "Татьянин день", 1994.

44. Соренков Э.И., Телига А.И., Шаталов А.С. Точность

вычислительных устройств и алгоритмов. – М.:

Машиностроение, 1976.

45. Справочник по специальным функциям/

Под ред. М.

Абрамовица и И. Стиган. – М.: Наука, 1979.

46. Фундаментальные проблемы теории точности/Под ред. В.П.

Булатова, И.Г. Фридлендера. – СПб.: Наука, 2001.

47. Хампель Ф. Робастность в статистике. – М.: Мир, 1989.

48. Хьюбер П. Робастность в статистике. – М.: Мир, 1984.

49. Шляндин В.М. Цифровые измерительные устройства:

Учебник для вузов. – М.: Высшая школа

, 1981.

50. Ширман Я.Д., Манжос В.Н. Теория и техника обработки

радиолокационной информации на фоне помех. – М.: Радио и

связь, 1981.