Романов В.Н. Теория измерений. Основы теории точности средств измерений
Подождите немного. Документ загружается.


() ()
0
sin 2
I
H
fh fd
τ
πττ
∞
=
∫
. (4.2.27)
Пример 3. Пусть сигнал на входе
x(t) состоит из полезного
сигнала
y(t) и шума n(t), причем y(t) и n(t) – независимые
стационарные процессы. Мы хотим аппроксимировать
y(t)
процессом, полученным фильтрацией
x(t). Матрица спектральной
плотности
x(t) и y(t) имеет вид:
()
() ()
()
()
yy nn yy
yy yy
SfSfSf
Sf Sf
+
. (4.2.28)
Наилучший линейный фильтр, предназначенный для
определения
y(t) по x(t), имеет частотную характеристику:
()
1
() () () ()
yy yy nn
Hf
S
f
S
f
S
f
−
=+. (4.2.29)
Функция
H(f) называется избирательным фильтром для сигнала
y(t), присутствующего в шуме n(t). Как видно, из выражения
(4.2.29), его действие состоит в том, что частотные компоненты
сигнала
x(t) из интервала частот, где значение S
nn
(f) велико по
сравнению с
S
yy
(f), этим фильтром не пропускаются, а
компоненты
x(t) из интервала частот, где S
nn
(f) мало по
сравнению с
S
yy
(f), пропускаются почти без изменений. Величина
S
yy
(f)/ S
nn
(f) называется отношением сигнала к шуму на частоте f.
Пример 4. Измерение сигнала x(t) проводится двумя
приборами с передаточными функциями
W
1
(p), W
2
(p). Сигналы на
выходе этих приборов соответственно равны:
11 1
() ()() ()yp Wpxp p=+Δ
,
22 2
() ()() ()yp Wpxp p=+Δ
, (4.2.30)
где
Δ
1
(p), Δ
2
(p) – лапласовское изображение шумов на выходе
приборов СИ1 и СИ2 соответственно. Приборы имеют разные
динамические характеристики и разные спектры собственных

шумов. Требуется повысить динамическую точность и провести
фильтрацию шумов.
Для решения этой задачи используем два избирательных
фильтра с передаточными функциями
W
1u
(p) и W
2и
(p). Первый
фильтр включен на выходе прибора СИ1, а второй – на выходе
СИ2.
Суммарный сигнал на выходе СИ1+СИ2 равен:
11 2 2
() ()() () () () ()
ии
yp W pxp W p p W p p=+Δ+Δ
. (4.2.31)
Передаточная функция всего устройства:
11 2 2
() () () () ()
uu
Wp W pW p W pW p=+ . (4.2.32)
Выберем:
11 2 2
() () 1 () ()
uu
WpW p W pW p
ε
=− +
, (4.2.33)
где
ε – малая величина. При ε=0: W(p)=1, т.е. на выходе получаем
неискаженный сигнал, характеризуемый высокой точностью и
эффективной фильтрацией шумов.
Статические измерения. В статическом случае для
повышения помехоустойчивости СИ применяются специальные
алгоритмы обработки многократных измерений. Задача
формулируется в следующем виде. Найти оценку
€
x
полезного
сигнала
x=const по результатам многократных измерений z
i
=
x
i
+Δ
i
(i=1,2,…,n), включающих значениях помех Δ
i
, которые
являются реализациями случайной величины Δ(
t).
Соответствующая оценка должна быть эффективной,
состоятельной и несмещенной в заданном диапазоне измерений.
Можно показать после несложных преобразований, что
оптимальный алгоритм, удовлетворяющий сформулированным
условиям, определяется выражением:
1
1
1
( ) ( ).... ( )
( ,..., )
( ) ( ).... ( )
n
n
n
tp t p z t p z t dt
fz z
p
tpz t pz tdt
++
=
++
∫
∫
, (4.2.34)
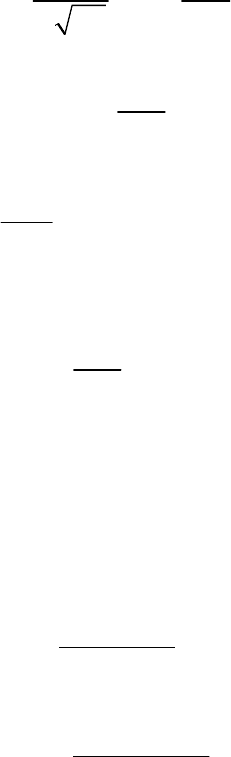
где p(t)·…·p(z
n
+t)=p(t, z
1
, ..., z
n
) – совместная плотность
распределения
z
0
, z
1
,…,z
n
. Искомая оценка равна:
010 0
€
( ,..., )
n
x
zfzz zz=− − −
. (4.2.35)
Рассмотрим примеры применения алгоритма (4.2.34) для
различных законов распределения помехи Δ.
Пример 5. Пусть помеха Δ(
t) имеет нормальное
рапределение вида:
2
2
1
( ) exp( )
2
2
t
pt
σ
σπ
=−
. (4.2.36)
Подставляя (4.2.36) в (4.2.34) и проводя вычисления, найдем:
1
1
1
( ,..., )
1
n
nk
k
f
zz z
n
=
=−
+
∑
. (4.2.37)
Для оптимальной оценки из (4.2.35) получим:
0
1
€
1
n
k
k
x
z
n
=
=
+
∑
, (4.2.38)
т.е. имеем выборочное среднее с дисперсией погрешности
оценки:
[]
2
€
1
Dx x
n
σ
−=
+
, (4.2.39)
где σ
2
– дисперсия помехи Δ.
Пример 6. Пусть помеха равномерно распределена в
интервале [
-α, α] с дисперсией D[Δ]=α
2
/3. Требуется найти
оптимальную оценку.
Можно показать, что в этом случае оптимальная оценка
определяется центральным размахом:
max min
ц
€
2
z
z
xR
+
==
(4.2.40)
с дисперсией погрешности оценки:
[]
2
2
€
(2)(3)
Dx x
nn
α
−=
++
. (4.2.41)
Отметим, что если в данном примере использовать оценку в
виде выборочного среднего, то дисперсия погрешности оценки
возрастет, и оказывается равной
D[Δ]=α
2
/3(n+1).
Сравним эффективность полученных оценок по объему
выборки (числу измерений), необходимому для обеспечения
заданной дисперсии погрешности оценки
D
0
.
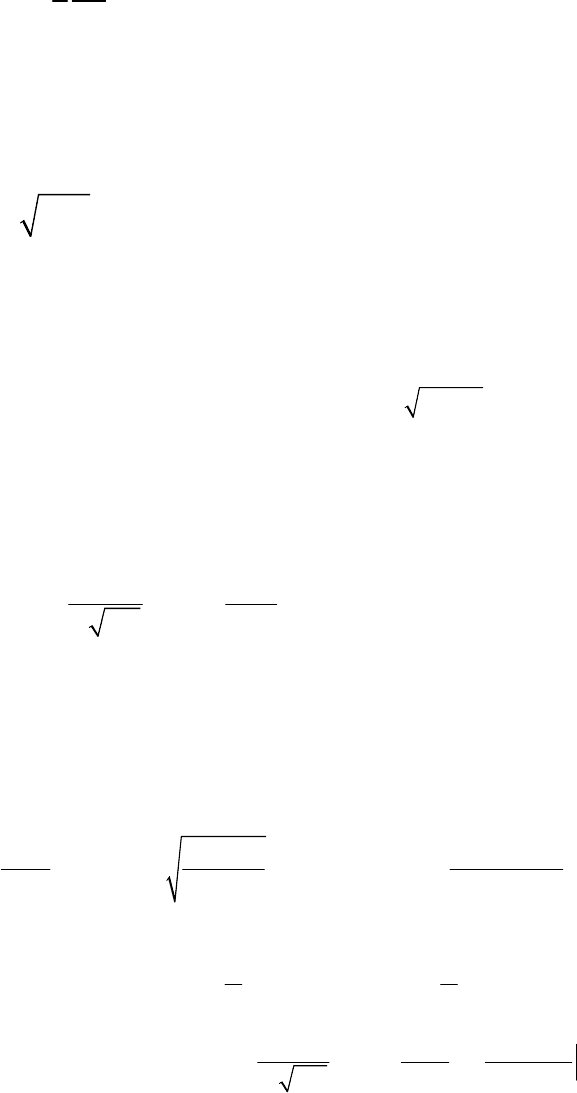
Для среднего выборочного необходимое число измерений
равно:
2
cp
0
1
1
3
n
D
α
+≥
. (4.2.42)
Для центрального размаха:
22
ц 0
2/nD
α
≥
. (4.2.43)
Сравнивая n
cp
и n
ц
, получаем соотношение для минимальных
объемов выборки двух оценок
ц cp
6nn≅
. (4.2.44)
Таким образом, оценка по центральному размаху
оказывается эффективнее, чем по среднему выборочному,
особенно, когда требуется обеспечить высокую точность
результата измерения, т.е. при больших объёмах выборки.
Например, если
п
ср
=100, то п
ц
=
2
610 25
⋅
≅ , т.е. в четыре раза
меньше.
Рассмотрим задачу нахождения оптимальной оценки в более
сложном случае, когда плотность распределения помехи имеет
вид:
2
2
(1 )
(, ) exp ()
2
2
z
pz hz
σ
ε
εε
σ
π
⎛⎞
⎜⎟
⎜⎟
⎝⎠
−
=−+
, (4.2.45)
где ε – малая величина; первое слагаемое описывает
флюктуирующую помеху с малой дисперсией; а второе –
импульсную с дисперсией
22
2
σ
σ
>> и распределением, отличным
от нормального. В этом случае удается получить
квазиоптимальную оценку с точностью до членов, линейных по
ε:
2
0
2
00
12
€
()exp
1(1)
2( 1)
nn
k
kkk
kk
na
xz aqa
nnn
n
π
εσ
σ
==
⎡
⎤
⎢
⎥
⎢
⎥
⎣
⎦
=−
++
+
∑∑
, (4.2.46)
где
()
0
11
n
j
j
kkk
j
jk
azzzz
nn
=
≠
=−=−
∑∑
;
2
00
2
1(,)
() () exp( )
2
2
z дpz
qz hz
д
ε
ε
ε
σ
σπ
=
=− − = .
Из (4.2.46) следует, что искомая оценка содержит поправку к
выборочному среднему, которая нелинейно зависит от
результатов измерений.
Если модель помехи имеет вид
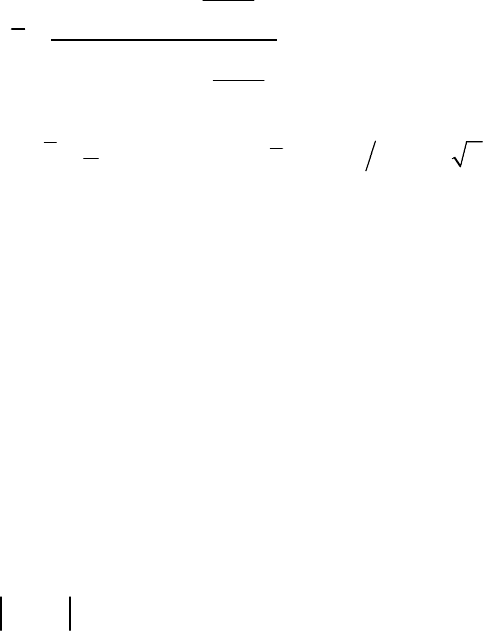
(, ) (1 ) () ()
p
zzz
ε
εδ εγ
=− +
, (4.2.47)
т.е. часть результатов измерений не искажена;
δ
(z) – дельта
функция, ()z
γ
– плотность нормального распределения
2
(0, )N
σ
,
то удается получить оптимальную оценку:
2
2
1
2
2
2
1
2
exp( )
2
€
exp( )
2
n
k
k
k
n
k
n
k
n
xz
n
σ
ε
σ
=
=
−
=+
+−
∑
∑
l
l
l
, (4.2.48)
где
1
1
;;((1))
n
n
kk k
k
n
zzzz n
εε ε
=
==−=−
∑
l .
Аналитическое выражение для дисперсии погрешности
оценки по выражениям (4.2.46) и (4.2.48) получить не удается,
поэтому зависимость дисперсии от параметров ε, σ
2
и объёма
выборки исследуется путем моделирования на ЭВМ. Расчеты
показывают, что применение алгоритма (4.2.48) позволяет
снизить дисперсию погрешности оценки в несколько раз при
значениях
ε=0,1…0,3, т.е. при высоком уровне помех.
Задача ещё более усложняется, если не известен закон
распределения помехи. В этом случае наиболее часто
используется метод наименьших модулей, в котором
минимизируется величина:
1
€
min
n
k
k
zx
=
−⇒
∑
. (4.2.49)
Решением уравнения (4.2.49) является оценка по медиане:
1
€
med( ,...., )
n
x
zz=
. (4.2.50)
Другим подходом, получившим распространение, является
α-усеченное среднее, когда с обоих концов выборки удаляют по
m результатов измерений, а по оставшейся части выборки
вычисляется среднее.
Из этих двух методов оценка по медиане очень «жесткая»,
так как выбрасываются все результаты измерений, кроме одного
или двух центральных. Оценка по усеченному среднему менее
жесткая, кроме того, она уменьшает влияние флюктуирующих
помех.
4.3. Статистические методы оценки надежности СИ
Повышение точности и помехоустойчивости СИ тесно связано с
надежностью работы измерительной аппаратуры. В этом разделе речь
пойдет о метрологической надежности, т.е. о выходе параметров за
допустимые пределы с заданной вероятностью
(достоверностью).Наибольший практический интерес имеют
следующие задачи:
- оценка вероятности безотказной работы СИ либо
вероятности отказа с учетом износа;
-
оценка вероятности брака контроля при поверке СИ;
- определение «склонности» СИ к отказам с учетом ряда
факторов (например, условий эксплуатации);
-
оценка вероятности отказов СИ за счет экстремальных
факторов.
Для решения перечисленных задач применимы несколько
статистических распределений (см. Приложение 4). Для оценки
вероятности безотказной работы наиболее подходят
распределение Вейбулла и отрицательное экспоненциальное
распределение. При оценке брака контроля также могут быть
использованы эти распределения. Склонность к отказам
оценивается по отрицательному биномиальному распределению.
Наконец, оценка
отказов СИ за счет экстремальных факторов
проводится с использованием распределения Пуассона.
Оценка вероятности безотказной работы аппаратуры.
Прогнозирование вероятности безотказной работы СИ
проводится при нескольких предположениях. Отказы СИ и
аппаратуры контроля могут происходить по следующим
причинам: технологический брак, условия эксплуатации,
старение и износ, экстремальные факторы (грубые ошибки,
случайный сбой в работе по внешним причинам, аварийные
ситуации и т.д.). Вероятность отказов отдельных элементов СИ
принимается одинаковой; аналогичное
допущение имеет место и
для элементов контрольно-измерительной аппаратуры.
Определение вероятности отказов СИ проводится с
использованием двух распределений: отрицательного
экспоненциального и распределения Вейбулла. Последнее
распределение имеет более общий характер и позволяет учесть
процессы износа элементов СИ. Вероятность отказов по
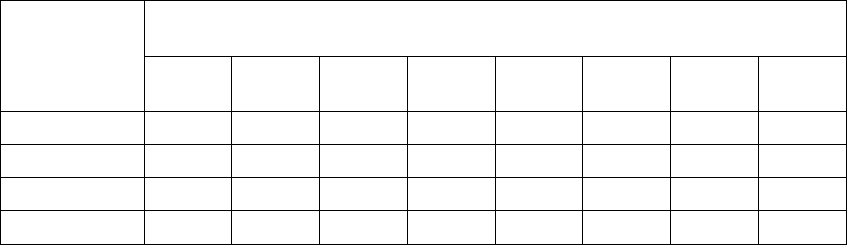
отрицательному экспоненциальному распределению
определяется интегральной функцией распределения:
0
( ) 1 exp( )
P
Fx x
λ
==−−, (4.3.1)
Вероятность безотказной работы, следовательно, равна:
0
1exp()
б
P
Px
λ
=− = − , (4.3.2)
Результаты расчетов приведены в табл. 3. Расчет проводился для
практически важных значений параметра
λ
и аргумента х.
Таблица 3
Вероятность отказов СИ (расчет по отрицательному
экспоненциальному распределению)
x,
год
λ
0,01 0,02 0,03 0,04 0,08 0,1 0,2 0,3
2
0,02 0,04 0,06 0,08 0,15 0,18 0,33 0,46
3
0,03 0,06 0,09 0,11 0,22 0,26 0,41 0,56
4
0,04 0,08 0,11 0,15 0,27 0,33 0,55 0,70
5
0,05 0,10 0,14 0,18 0,33 0,39 0,63 0,78
Интервал времени при расчетах выбран в пределах 2…5 лет, что
соответствует межповерочному интервалу для СИ, применяемых
в различных областях (механика, акустика, теплофизические
измерения).
При исследовании распределения Вейбулла соотношение для
вероятности отказов имеет вид:
0
)1 exp( (( )/ )
c
Pxab=− − − , (4.3.3)
и вероятность безотказной работы в течение времени
х
составляет:

)exp( (( )/ )
c
б
Pxab=−−
, (4.3.4)
где a, b, c – параметры распределения. При расчетах полагалось
a=0, b>1, c>1, что соответствует реальным условиям
эксплуатации СИ. Результаты расчетов приведены в табл.4.
Таблица 4
Вероятность отказов СИ (расчет по распределению Вейбулла)
х , год
b
c
1,2 1,5 2 5 7
2
3
4
5
2
0,6
0,8
0,89
0,95
0,6
0,84
0,94
0,98
0,6
0,84
0,94
0,98
0,6
0,99
1
1
0,6
1
1
1
2
3
4
5
5
0,28
0,41
0,53
0,6
0,22
0,37
0,51
0,6
0,14
0,30
0,46
0,6
0,01
0,07
0,28
0,6
0
0,03
0,2
0,6
2
3
4
5
7
0,18
0,29
0,39
0,48
0,15
0,22
0,37
0,39
0,06
0,15
0,27
0,3
0
0,01
0,08
0,27
0
0
0,02
0,16
Отметим, что распределение Вейбулла можно рассматривать
как отрицательное экспоненциальное, в котором параметр
λ
зависит от
х (учет износа), причем
λ
= х
c-1
/b
c
. С использованием
данных табл.3 оценим вероятность отказов для двух типов СИ,
работающих в разных режимах: циклически и непрерывно
(например, в системах управления, следящих системах). Для
циклических СИ параметр
λ изменяется в пределах
λ
ц
=0,006…0,03, а для непрерывных – в пределах
λ
н
=0,02…0,1 (в
зависимости от условий эксплуатации). Расчеты дают значение
вероятности отказов: для циклических СИ –
P
0ц
= 0,03…0,14; для
непрерывных –
P
0н
= 0,1…0,39 (расчеты проведены для значения
х=5 лет, то есть межповерочный интервал принят равным 5 лет.
Как видно из расчетов, вероятность отказов у циклических СИ
существенно ниже (примерно в 3 раза), чем у непрерывных.
Расчеты по распределению Вейбулла выполняются аналогично и
дают такую же закономерность.
Представляет интерес и обратная задача – оценка параметров
распределения, связанных с характеристиками СИ, при которых
вероятность отказов не превышает некоторого заданного
значения. Положим, что вероятность отказов не должна
превышать
P
0
=0,1…0,01, что соответствуют вероятности
безотказной работы
P
б
=0,90…0,99. Из табл. 3 имеем, что для
х=5лет при P
0
=0,1 –
λ
=0,02, что соответствует для распределения
Вейбулла значению
х
c-1
/b
c
=0,02, которое обеспечивается,
например, при
х=4, b=7, c=5. Для х=5лет при P
0
=0,05 – λ= 0,01,
что соответствует для распределения Вейбулла значению
х
c-1
/b
c
=0,01, которое достигается, например, при х=2, b=7, c=2.
Для
х=2 года при P
0
=0,02 (P
б
=0,98) –
λ
=0,01, что соответствует
значению
х
c-1
/b
c
=0,01, которое достигается, например, при х = 4,
b=7, c=7. Параметры распределения могут быть определены по
результатам испытаний, что позволяет оценить доверительную
вероятность и необходимый межповерочный интервал. Если же
заданы доверительная вероятность и межповерочный интервал,
то можно определить параметры распределения и по ним оценить
необходимые характеристики данного типа СИ при
конструировании.
Оценка брака контроля. При вероятностном подходе к оценке
брака контроля следует учитывать четыре исхода:
Р
1
=Р
11
P
12
– вероятность не обнаружения дефекта на годном
элементе;
Р
2
=Р
21
Р
22
– вероятность обнаружения дефекта на негодном
элементе;
Р
3
= Р
31
Р
32
– вероятность обнаружения дефекта на годном
элементе;
Р
4
=Р
41
Р
42
- вероятность не обнаружения дефекта на негодном
элементе,
где первые множители характеризуют соответствующие
вероятности для СИ, а вторые – для аппаратуры контроля. Для
вероятности брака контроля имеем следующее соотношение:
() ()
14
nn
бр
P
PP P
Δ
=− +
, (4.3.5)
где n – порядковый номер контроля (поверки); Р
∆
- вероятность
того, что параметры СИ находятся в заданных пределах;
Р
1
=
Р
11
P
12
, Р
4
=Р
41
Р
42
. Положим для простоты, что n=1. Вероятность
Р
∆
зависит от типа СИ:
0
2()
P
fydy
Δ
Δ
=
∫
, (4.3.6)
где
f (y) – плотность распределения параметров. В общем случае
f(y) является многомерным распределением, однако если выбрать
основной параметр, то распределение сводится одномерному. В
качестве основного (технологического) параметра для СИ обычно
используется характеристика инструментальной погрешности
(дисперсия, доверительный интервал и т.п.). Для определения
Р
∆
можно использовать нормальное распределение. Для
идентификации параметров распределения необходим большой
объем выборки по испытаниям СИ данного типа, что является
трудоемкой задачей. Поэтому примем для расчета
Р
∆
более
простую модель. Обозначим
p
i
– вероятность выхода за
допустимые пределы выбранного параметра для элемента
i схемы
СИ. Примем для простоты
p
i
=p=const(i). Тогда, вероятность того,
что для всей схемы параметр не выйдет за допустимые пределы,
равна:
(1 )
o
N
P
p
Δ
=− , (4.3.7)
где
N
0
– число элементов схемы СИ. Положим для
определенности N
0
=10, тогда Р
∆
=0 при p=1; Р
∆
=0,95 при p= 0,005;
Р
∆
=0,90 при p=0,01; Р
∆
=0,82 при p=0,02; Р
∆
=1 при p=0. Мы
рассматриваем последовательную схему; для параллельной
схемы
1
o
N
P
p
Δ
=− . Оценим вероятность брака контроля из
соотношения (4.3.5). Рассмотрим ряд предельных случаев. Пусть
вероятность выхода параметра за допустимые пределы равна
нулю, т.е. p=0, тогда Р
∆
=1. Кроме того, положим, что контрольно-
измерительная аппаратура не содержит отказов. Тогда
P
12
=1; P
42
= 0 и соотношение (4.3.5) упрощается:
11 41
101
бр
P
PP••=− +
, (4.3.8)
где Р
11
, Р
41
− вероятность безотказной работы и отказов СИ
соответственно. Используем для расчетов в целях упрощения
