Романов В.Н. Теория измерений. Основы теории точности средств измерений
Подождите немного. Документ загружается.

2
() 2 () () ()
jf
xy xy xy xy
G
f
Re dC
fj
Q
f
πτ
ττ
∞
−
−∞
==−
∫
. (2.20)
Действительная часть G
xу
(f):
() 2 ()cos2
xy xy
C
f
R
f
d
τ
πττ
∞
−∞
=
∫
(2.21а)
называется коспектральной плотностью или коспектром, а
мнимая часть
() 2 ()sin2
xy xy
Q
f
R
f
d
τ
πττ
∞
−∞
=
∫
(2.21б)
называется квадратурной спектральной плотностью или
квадратурным спектром. Через С
xy
(f) и Q
xy
(f) соотношение (2.19)
записывается следующим образом:
2*2
00
0
11
() () ()
22
[()cos2 ()sin2 ]
jf jf
xy xy xy
xy xy
RG
f
ed
f
G
f
ed
f
Cf f Qf fdf
πτ πτ
τ
πτ πτ
∞∞
−
∞
=+ =
=+
∫∫
∫
. (2.22)
Отметим, что зная C
xy
(f) можно найти R
xy
(0). Удобно
выражать взаимные спектры через модуль и фазовый угол
()
() ()
xy
j
f
xy xy
Gf Gfe
θ
−
= , (2.23)
22
() () ()
xy xy xy
Gf Cf Qf=+, (2.24)
() [ ()/ ()]
xy xy xy
f
arctg Q f C f
θ
= . (2.25)
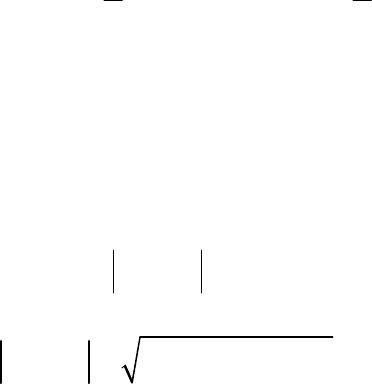
График типичной взаимной спектральной плотности
приведен на рис.5.

⏐G
xy
(f)⏐ θ
xy
(f)
0 f 0 f
а б
Рис.5. Типичная взаимная спектральная плотность: а – модуль, б – фаза
Знаки С
xy
(f) и Q
xy
(f) могут быть положительными и
отрицательными и определяют квадрант, в котором находится
фазовый угол θ
xy
(f). Положительное значение θ
xy
(f) соответствует
запаздыванию y(t) относительно x(t) на частоте f, а
отрицательное значение показывает, что y(t) опережает x(t) на
частоте f. Иными словами, эти знаки показывают, следует ли
процесс y(t) за x(t), т.е. выполняется ли соотношение y(t)=x(t – τ
0
)
при некотором τ
0
>0, что соответствует положительному
запаздыванию сигнала, передаваемого из точки x в точку у на
частоте f. Из равенства y(t)=x(t – τ
0
) следует, что у(0) вызвано
x(– τ
0
), а у(τ
0
) вызвано x(0), при условии измерения сигналов в
этих точках в одной шкале времени.
Модуль взаимного спектра входит в важное неравенство для
взаимных спектров:
2
() () ()
xy xx yy
Gf GfGf≤ , (2.26)
которое аналогично неравенству для взаимных ковариационных
функций (2.6) и позволяет определить функцию когерентности:
2
22
()
() , 0 () 1
() ()
xy
xy xy
xx yy
Gf
ff
GfGf
γγ
=≤≤, (2.27)
которая аналогична квадрату нормированной корреляционной
функции, задаваемой соотношением (2.7).
Определение спектральных плотностей посредством
преобразования Фурье. Пусть {x(t)}, {y(t)} – два стационарных
эргодических случайных процесса. Финитные преобразования

Фурье k-х реализаций длины Т каждого процесса определяются в
виде:
2
0
(,) ()
T
jft
kk
XfT xte dt
π
−
=
∫
,
2
0
(,) ()
T
jft
kk
YfT yte dt
π
−
=
∫
. (2.28)
Двусторонняя взаимная спектральная плотность этих двух
процессов определяется соотношением:
*
1
() lim [ (,) (,)]
xy k k
T
Sf EXfTYfT
T
→∞
=
, (2.29)
где
Е – математическое ожидание, обозначающее усреднение по
индексу
k. Односторонние взаимные спектральные и
спектральные плотности определяются следующим образом:
*
2
() lim [ (,) (,)]
xy k k
T
Gf EXfTYfT
T
→∞
= , (2.30)
2
*
2
() lim [ (,) (,)] [ (,)]
xx k k k
T
Gf EXfTXfT EXfT
T
→∞
==. (2.31)
Отметим, что в определение спектральных плотностей
используется произведение
Х
*
Y, но не ХY
*
. Функции плотностей,
определенные соотношениями (2.29)–(2.31) идентичны
соответствующим функциям, определенным по (2.8)–(2.13) как
преобразования Фурье. Это утверждение называется теоремой
Винера–Хинчина. Все соотношения и свойства для спектральных
плотностей, введенные ранее, сохраняются.
Определение спектральных плотностей посредством
аналоговой фильтрации.
До внедрения цифровых способов
обработки сигналов спектральные плотности, в основном,
автоспектры оценивались при помощи аналоговых анализаторов.
Этот способ используется и в настоящее время. Суть его сводится
к следующему. Реализация случайного процесса
х(t) проходит
через узкополосный фильтр с полосой пропускания Δ
f и
изменяемой частотой среза
f. Выходной сигнал этого фильтра
х(f,Δf, t) возводится в квадрат и усредняется по времени, а затем
делится на Δ
f; в итоге получается оценка спектральной плотности
вида

2
0
1
€
() (, ,)
()
T
xx
Gf xfftdt
fT
=Δ
Δ
∫
. (2.32)
Если в полученной оценке перейти к пределу
T→ ∞, Δf → 0 так,
что (Δ
f)T→∞, то в результате получим одностороннюю
спектральную плотность, совпадающую с определенными ранее
из соотношений (2.13), (2.30)
2
0
0
1
() limlim (, ,)
T
xx
fT
Gf xfftdt
T
Δ→ →∞
⎡⎤
=Δ
⎢⎥
⎣⎦
∫
. (3.33)
Некоторые ковариационные функции и функции
спектральной плотности, применяемые в теоретических
исследованиях, приведены в таблице.
Вопросы данного раздела рассмотрены, например, в [5, 7, 8,
9, 12, 45].
Примеры ковариационной функции и функции спектральной
плотности.
Тип
Ковариационна
я функция,
R
xx
(τ)
Односторонняя
спектральная
плотность,
G
xx
(f)
Постоянная
C
2
C
2
δ(f)
Гармоническая
X
2
/2cos2πf
0
τ X
2
/2 δ(f−f
0
)
Белый шум
aδ(τ) 2a, f≥0
0 в остальных случаях
Низкочастотный
белый шум
absin2πbτ/(2πbτ) a, 0≤f≤b
0 в остальных случаях
Ограниченный
по частоте
белый шум
absinπbτ/(πbτ)·
·cos2πf
0
τ
a, 0≤f
0
−(b/2) ≤ f≤ f
0
+(b/2)
0 в остальных случаях
Экспоненциальная
exp(−a
|
τ
|
)
4a/(a
2
+4π
2
f
2
)
Экспоненциально-
косинусоидальная
exp(−a
|
τ
|
)cos2πf
0
τ
2a[1/(a
2
+4π
2
(f+ f
0
)
2
)+
+1/(a
2
+4π
2
(f−f
0
)
2
)]
Экспоненциально-
косинусоидально-
синусоидальная
exp(−a
|
τ
|
)(gcos2πf
0
τ+
+hsin2πf
0
|τ|)
[2ag+4πh(f+f
0
)]·[(a
2
+4π
2
·
(f+f
0
)
2
)]
−1
+[2ag−4πh(f−f
0
)]·
·[(a
2
+4π
2
(f−f
0
)
2
)]
−1

3. Определение переходной функции системы
Пусть передаточная функция системы представима в виде
отношения двух многочленов:
()
()
()
Bp
Wp
A
p
=
, (3.1)
где –
B(p)=b
0
p
m
+…+b
m
; A(p)=a
0
p
n
+…+a
n
,причем m<n.
Передаточная функция связана с переходной функцией
преобразованием Лапласа:
0
() () ;
p
Wp h e d p j
τ
τ
ταβ
∞
−
==+
∫
. (3.2)
Тогда переходная функция системы находится с помощью
обратного преобразования Лапласа:
1
() [ ( )]hLWp
τ
−
= , (3.3)
1
1
1
1
[()] ()
2
j
pt
j
LWp Wpedp
j
σ
σ
π
+∞
−
−∞
=
∫
. (3.4)
Для вычисления обратного преобразования Лапласа сначала
находятся корни
p
k
характеристического уравнения A(p)=0:
непосредственно (при
n≤4) или численными методами (при
n>4). Если все корни простые, то есть А(р)=a
0
(р−р
1
)⋅(р−р
2
)⋅…⋅
(
р−р
n
), то имеет место соотношение:
11
1
()
()
[()] [ ] ;( 0)
() ( )
k
n
pt
k
k
k
Bp
Bp
LWp L e t
Ap A p
−−
=
== >
′
∑
. (3.5)

Если корни кратные, то есть
1
01
( ) ( ) ...( )
n
l
l
n
A
p app pp=− −, то
1
L
−
определяется выражением (формула Хевисайда):
(1)
1
1
()()
1
[()] [ ]
(1)! ()
k
l
k
k
l
pt
n
k
p
p
k
k
pp Bpe
LWp
lAp
−
−
=
=
−
=
−
∑
(3.6)
Выражение (3.6) можно представить в виде:
1
1
1
[()] ,( 0)
k
kk
l
n
lipt
ki
i
k
LWp Ht e t
−
−
=
=
=>
∑∑
, (3.7)
где
1
1
()()
1
[]
(1)!( 1)! ()
k
k
l
i
k
p
p
ki
i
k
pp Bp
d
H
il Ap
dp
−
=
−
−
=
−−
. (3.8)
Отметим, что система устойчива, если корни
р
k
имеют
отрицательные действительные части.
В частности, если
123
1
()
()( )()
Wp
pp pp pp
=
−−−
, то
3
12
1
12 3
() [ ( )]
p
t
p
tpt
ht L W p Ce Ce Ce
−
==++, (3.9)
где
1
1213
1
()()
C
pppp
=
−−
;
2
2123
1
()()
C
pppp
=
−−
;
3
3132
1
()( )
C
pppp
=
−−
. (3.10)
Вместо формулы Хевисайда можно использовать разложение,
применяемое при решении дифференциальных уравнений. Если
А(р) и В(р) не имеют совпадающих корней, то каждому
действительному корню
р
k
уравнения А(р)=0 отвечает l
k
простых
дробей вида:
2
12
)
,,...,
(
()
l
k
k
l
k
k
k
c
cc
pp
pp
pp
−
−
−
, (3.11)
где
l
k
– кратность корня р
k
. Каждой паре комплексно-
сопряженных корней
р
k
=
α
+i
β
отвечает l
k
простых дробей вида:
12
12
22 222
22
, ,...,
() [() ]
[( ) ]
k
k
k
l
l
l
pg
pg pg
dd d
pp
p
αβ αβ
αβ
+
++
−+ −+
−+
,
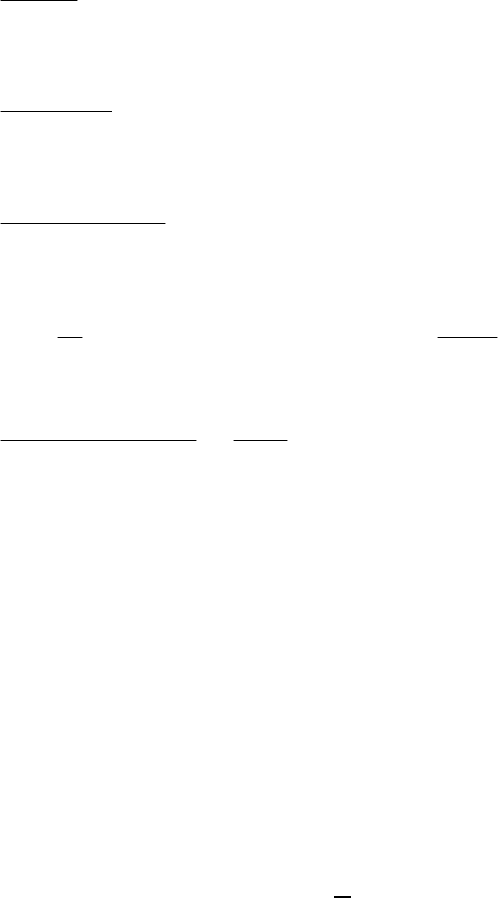
где l
k
– кратность корней р
k
=
α
+i
β
.
Тогда
1
[()]LWp
−
находится как сумма обратных преобразований
Лапласа таких слагаемых.
В частности,
1
1
1
1
[]
p
t
Le
pp
−
=
−
, (3.12)
1
1
2
1
1
[]
()
p
t
Lte
pp
−
=
−
, (3.13)
1
1
22
[]sin()
()
t
pg
LCet
p
α
β
ϕ
αβ
−
+
=+
−+
, (3.14)
где
221/2
1
1
[( ) ] ,Cg arctg
g
β
αβϕ
α
β
=++ =
+
;
1
222 3
11
[](sincos)
[( ) ] 2
t
Lettt
p
α
β
ββ
αβ β
−
=−
−+
. (3.15)
Вопросы этого раздела рассмотрены, например, в [20, 45].
4. Типы распределений, используемых при оценке
надежности СИ
Распределение Вейбулла. Оно является непрерывным.
Плотность распределения задается выражением:
1
(;,,) / (( )/ ) exp{(( )/ )}
cc
f
xabc c b x a b x a b
−
=− −− , (4.1)
где
х – случайная величина; x>a, b>0, c>0, a – параметр сдвига, b
– параметр масштаба,
с – параметр формы. При испытаниях на
долговечность параметр
а обозначает длительность начального
периода, в течение которого происходят отказы. Интенсивность
отказов и плотность распределения Вейбулла принимают
различные формы при разных
с. В частности, при с>1
распределение одновершинное, и интенсивность отказов
возрастает с течением времени. При
с<1 распределение имеет вид
кривой убывающей функции, и интенсивность отказов с
течением времени уменьшается. При
с=1 интенсивность отказов
постоянна, и распределение Вейбулла совпадает с
экспоненциальным(см. ниже). В этом случае параметр масштаба
b=1/λ, где λ – параметр экспоненциального распределения.
Распределение Вейбулла часто используется в качестве модели
для времени безотказной работы на основе экспериментальных
данных. Вероятность отказа за время
t определяется выражением:
0
( ) ( ; , , ) 1 exp{ (( )/ ) }
t
c
a
P
tfxabcdx tab==−−−
∫
. (4.2)
Математическое ожидание для этого распределения равно:
2
[] / (1/)Ex ab b c c=+ Γ . (4.3)
Дисперсия равна:
222
[] 2/(1/) /(1/)2/(2/)Dx a ab ab c c b c c b c c=−+ Γ − Γ + Γ . (4.4)
Отрицательное экспоненциальное распределение. Оно также
является непрерывным. Плотность экспоненциального
распределения равна:
(, ) exp( ); 0, 0
f
xxx
λ
λλ λ
=− ≥>
, (4.5)
где
λ имеет смысл интенсивности отказов. Иногда употребляется
другой параметр
b=1/λ. Экспоненциальное распределение
является частным случаем гамма-распределения при
с=1. В
теории надежности это распределение является статистической
моделью времени безотказной работы для системы с большим
числом последовательно соединенных элементов. Вероятность
отказа системы за время
t дается выражением:
0
() 1 exp( )
P
tt
λ
=− −
. (4.6)
Для этого распределения характерна резко выраженная
правосторонняя (положительная) асимметрия, кроме того,
математическое ожидание равно среднеквадратичному
отклонению. Математическое ожидание определяется
выражением:
0
[] [] exp( ) 1/Ex Dx x xdx
λ
λ
λ
∞
== − =
∫
. (4.7)
Биномиальное и отрицательное биномиальное
распределение
. Эти распределения являются дискретными.
Предположим, что проводится серия независимых испытаний, в
каждом из которых возможны лишь два исхода: успех или
неудача. Обозначим вероятность успеха
р, а вероятность неудачи
q=1–р. Предполагается, что р одинаково в каждом испытании.
Например, при контроле СИ
р – вероятность, что СИ будет
годным, а
q – что негодным. Тогда вероятность того, что в
последовательности из
n испытаний успехи осуществляются в
точности
k раз, дается выражением:
() ,0 1
kknk
n
P
xk Cpq p
−
== <<. (4.8)
Функция (4.8), определенная при
k=0,1,…,n, задает биномиальное
распределение с параметрами
n и p. Это очень важное дискретное
распределение, широко используемое при статистическом
контроле качества продукции, при описании систем массового
обслуживания и т.п. Биномиальное распределение симметрично
при
р=0,5; при р<0,5 – более пологое справа; при р>0,5
распределение более пологое слева. При расчетах вероятностей
удобно рекуррентная формула:
(1)( )()/((1))
P
knkpPkkq+= − + . (4.9)
Математическое ожидание для этого распределения равно
E[x=k]=np; а дисперсия D[x=k]=npq, т.е. дисперсия меньше
среднего. Отрицательное биномиальное распределение получило
свое название в связи с тем, что формула распределения
вероятностей для него определяется разложением бинома с
отрицательной степенью. В этом распределении число испытаний
является случайной величиной, и число успехов
k становится
параметром. Распределение позволяет определить вероятность
числа неудач
r до k-го успеха, которая равна члену
биномиального разложения выражения
p
k
(1–q)
-k
, включающему
q
r
, а именно:
1
() ; 0;0 1
rkr
kr
P
xr C pq n p
+−
== ≥ <<. (4.10)
Математическое ожидание равно:
E[x=r] = kq/p, а дисперсия:
D[x]=kq/p². Легко видеть, что для этого распределения
наблюдаемая дисперсия больше наблюдаемого среднего.
Отрицательное биномиальное распределение имеет интересные
приложения. Например, оно позволяет оценить «склонность» к
отказам, авариям, несчастным случаям объектов некоторого типа.
Распределение Пуассона. Это распределение является
дискретным. Если в биномиальном распределении положить
np=λ и при постоянном λ увеличивать n (n →∞), то биномиальное
распределение перейдет в распределение Пуассона с параметром
λ. Это распределение используется для определения вероятности
появления относительно редких случайных событий в единицу
времени, на единицу площади или объема, например, число
случаев брака, число внезапных отказов, число стихийных
бедствий и т.д. на единицу времени или пространства.
Вероятность числа таких событий за фиксированный интервал
времени дается выражением
() /!,0
r
Px r e r
λ
λ
λ
−
== <<∞. (4.11)
Математическое ожидание для этого распределения равно
дисперсии:
Е[х]=D[х]=λ, и определяется параметром λ.
Распределение имеет положительную асимметрию
λ
⎯0,5
, которая
стремится к нулю с ростом
λ, т.е. с увеличением λ распределение
становится более симметричным, отдельные вероятности при
λ<1
с ростом
r уменьшаются; при λ>1 – сначала увеличиваются, затем
уменьшаются. Максимум распределения приходится на
ближайшее целое, меньше
λ. При четном λ имеются два равных
максимума вероятностей. Отметим, что сумма случайных
величин, каждая из которых имеет распределение
f
i
, имеет
обобщенное распределение Пуассона
0
() [( )/!]
tnn
t
ii
n
he tnf
λ
λ
∞
−∗
=
=
∑
, (4.12)
где
n
i
f
∗
– свертка n функций f
i
. В частности, если распределение
f
i
пуассоновское, то
2
(;2 )
i
ffr
λ
∗
=
, где
(;2 )
f
r
λ
– распределение
вида (4.11).
