Романов В.Н. Теория измерений. Основы теории точности средств измерений

на произвольный входной процесс x(t) определяется интегралом

свертки (интеграл Дюамеля):

() ( ) ( )

y

thxtd

τ

ττ

∞

−∞

=−

∫

, (1.40)

т.е. реакция системы

y(t) есть взвешенная линейная сумма всех

прошлых и будущих значений входного процесса

x(t), где роль

весов выполняют значения весовой функции в различные

моменты времени.

Так как реальная система реагирует на возмущение только

когда оно поступило на вход системы, то имеет место равенство:

() 0 при 0

ht

τ

=<. (1.41)

Следовательно, нижний предел интегрирования в интеграле

свертки равен нулю. Постоянство параметров системы означает,

что её весовая функция не зависит от момента поступления

сигнала на вход системы, т.е. выполняется соотношение:

(, ) ( ) приht h t

τ

=−∞<<∞, (1.42)

Устойчивость системы означает, что если сигнал на входе

ограничен, то и выходной сигнал также является ограниченным.

Это условие выполняется, если справедливо соотношение:

()hd

ττ

∞

−∞

<∞

∫

. (1.43)

Наконец, линейность системы означает, что весовая функция

h(τ)

не зависит от процесса на входе

x(t):

0

() ( ) ( ) при всех ()

y

thxtd xt

τττ

∞

=−

∫

. (1.44)

В частности, для линейной системы случайный входной

процесс с гауссовским распределением порождает гауссовский

процесс на выходе. В реальных ситуациях, например, при резком

изменении входного сигнала или при исследовании разрушений

конструкций под действием случайных нагрузок, линейность не

выполняется. Однако если изучаемый объект не является сильно

нелинейным, то можно использовать линейное приближение

.

Динамические свойства изучаемых объектов принято

описывать не самой весовой функцией

h(τ), а некоторым ее

линейным преобразованием, вид которого зависит от конкретной

задачи. Наиболее удобно для идеальной системы, обладающей

перечисленными выше свойствами, пользоваться

преобразованиями Фурье, которые позволяют непосредственно

описывать динамические характеристики системы в некоторой

частотной области. Преобразования Фурье весовой функции

h(τ),

удовлетворяющей условию

h(τ)=0 при τ<0, имеет вид:

2

0

() ()

jf

Hf

he d

πτ

τ

∞

−

=

∫

(1.45)

и называется комплексной частотной характеристикой системы.

В общем случае её можно представить в виде:

() () ()

RI

H

fHfjHf=− , (1.46)

где

H

R

и H

I

– действительная и мнимая части функции H(f)

соответственно, определяемые из соотношений:

0

() ()cos2

R

Hf

h

f

d

τ

πττ

∞

=

∫

,

0

() ()sin2

I

Hf

h

f

d

τ

πττ

∞

=

∫

, (1.46а)

На практике часто используют полярную форму записи для

частотной характеристики

Н(ƒ):

()

() ()

j

f

Hf Hf e

ϕ

−

= , (1.47)

где │

Н(ƒ)│ – модуль, называемый амплитудной

характеристикой, а

φ(ƒ) – аргумент, называемый фазовой

характеристикой:

221/2

() [ () ()]

RI

Hf H f H f=+ ,

()

() [ ]

()

I

R

H

f

farctg

H

f

ϕ

= . (1.47a)

Частотная характеристика удобна для описания динамических

свойств измерительной системы, на вход которой подается

гармоническое колебание с частотой

ƒ. В этом случае сигнал на

выходе будет также гармоническим с частотой

ƒ, но имеющим

другую амплитуду и сдвиг по фазе относительно входного

сигнала, а именно:

() sin2 , () sin(2 )

x

tX ftytY ft

π

πθ

==−. (1.48)

Отношение амплитуд входного и выходного сигналов дает

амплитудную характеристику, а сдвиг по фазе – фазовую:

() ()/ (); () ()

H

fYfXf f f

ϕ

θ

==. (1.49)

При подаче на вход системы единичного скачка (функции

Хевисайда) наиболее удобно описывать динамические свойства

передаточной функцией, которая представляет собой

преобразование Лапласа весовой функции:

0

() () ,

p

Wp h e d p a

j

b

τ

ττ

∞

−

==+

∫

. (1.50)

Положив

a=0 и b=2πƒ получим, что на мнимой оси W(j2πƒ)=H(ƒ),

т.е. передаточная функция из соотношения (1.50) совпадает с

частотной характеристикой, определяемой соотношением (1.45).

Если

a≠0, то функции H(ƒ) и W(p) различаются.

Модели объектов. Достаточно общей моделью является

модель вида:

() () ; 1,2,...,

tt

yyt ftut T≡=+ = . (1.51)

В этой модели результат измерения представляет собой сумму

детерминированной последовательности {

ƒ(t)}, которую можно

назвать систематической составляющей и случайной

последовательности {

u

t

}, подчиняющейся некоторому

вероятностному закону (их часто называют сигнал и шум). Эти

компоненты не наблюдаются по отдельности. При повторении

эксперимента функция

ƒ(t) должна оставаться одной и той же, а

случайные составляющие представляются как различные

реализации случайного процесса. Случайные составляющие

включают и ошибки измерений, причем

ƒ(t)=E[y(t)]. Можно

выделить два типа временных последовательностей

ƒ(t), часто

называемых трендом. Один тип представляет медленно

меняющиеся функции времени, например, в виде полиномов

достаточно низкой степени. К другому типу принадлежат

циклические последовательности, например, конечные отрезки

ряда Фурье в виде αcos

ωt+βsinωt (0<ω<π) или в виде ρcos(ωt–φ) с

периодом 2

π/ω. В этом случае последовательные значения y(t)

разбросаны случайным образом относительно кривой

y=ƒ(t). Если

даже кривая известна и известен закон распределения ошибки, то

информация о значениях

y

1

,..,y

t–1

не позволит предсказать

значение

y(t). Такая модель используется, например, в

астрономии, где ƒ(t) описывает пространственное положение (по

одной из координат) планеты в момент времени

t, а ошибка

телескопа никак не влияет на положение планеты. В случае

маятника, совершающего свободные колебания, его смещение

описывается функцией

ρcos(ωt–φ).

Одной из общих моделей, в которой влияние временного

параметра проявляется в случайной составляющей, является как

уже отмечалось, стационарный случайный процесс. Для его

аппроксимации часто используется процесс авторегрессии.

Пусть

y

1

имеет известное распределение с нулевым средним,

а

y

1

и y

2

имеют совместное распределение совпадающее с

совместным распределением случайных величин

y

1

и ρy

1

+u

2

, где

u

2

не зависит от y

1

и имеет нулевое математическое ожидание.

Совместное распределение

y

1

, y

2

,…, y

t–1

, y

t

для t=3,4,… будем

полагать в свою очередь таким же, как совместное распределение

y

1

, y

2

,…, y

t–1

, ρy

t–1

+ u

t

, причем величина u

t

не зависит от y

1

,…, y

t–1

,

и имеет нулевое математическое ожидание. Тогда

последовательность {

y

t

} образует стационарный случайный

процесс, а именно процесс авторегрессии:

1ttt

yyu

ρ

−

=+. (1.52)

Уравнение (1.52) является стохастическим разностным

уравнением первого порядка. В такой модели

u

t

оказывает

влияние на

y

t

и на все последующие y

r

(r>t). Условное

математическое ожидание

y

t

при заданных значениях y

1

,…,y

t–1

удовлетворяет равенству

11 1

[ ,..., ]

ttt

E

yy y y

ρ

−−

=

. (1.53)

Процесс авторегрессии второго порядка получается, если

взять совместное распределение

y

1

,…,y

t–1

,

y

t

таким же, как

совместное распределение

y

1

,…,y

t–1,

ρ

1

y

t–1

+ ρ

2

y

t–2

+u

t

, где u

t

не

зависит от

y

1

, y

2

,…,y

t–1

, t=3,4,…. Переменная y

t

может описывать

смещение колеблющегося маятника, который подвержен

случайным ударным воздействиям

u

t

. Тогда ряд близок к

тригонометрической функции

ρcos(ωt–φ) с переменной

амплитудой, переменной частотой и переменной фазой. Процесс

авторегрессии четвертого порядка (АР

4

), порожденный моделью:

4

1

tstst

s

yyu

ρ

−

=

=+

∑

(1.54)

будет походить уже на сумму двух тригонометрических функций

с изменяющимися амплитудами, частотами и фазами.

Стационарный случайный процесс общего вида можно

аппроксимировать процессом авторегрессии достаточно

высокого порядка:

1

k

tstst

s

yyu

ρ

−

=

=+

∑

(1.55)

или процессом:

1

(cos sin )

q

tjjjj

j

yAtBt

ω

=

=+

∑

, (1.56)

где

A

j

и B

j

– независимые случайные величины с нулевыми

математическими ожиданиями и

E[A

j

2

]=E[B

j

2

]=φ(ω

j

).

Вклад тригонометрической функции с частотой

ω

j

/2π в

среднем пропорционален математическому ожиданию квадрата

ее амплитуды, т.е. 2

φ(ω

j

). Поэтому стационарный случайный

процесс можно характеризовать спектральной плотностью

S(ω),

т.е. такой функцией, для которой:

() ( );

j

b

jj

a

Sd a b

ω

ωω ϕω ω

=≤≤

∑

∫

. (1.57)

Характерное свойство ССП состоит в том, что ковариация

Е[(y

t

–

E[y

t

])(y

s

-E[y

s

])] зависит только от разности │t–s│и ее можно

обозначить как

σ(t–s).

Таким образом ковариационная последовательность и

спектральная плотность (если она существует) являются двумя

альтернативными формами описания структуры моментов

второго порядка ССП. Ковариационная последовательность

более удобна и информативна, когда большее значение имеет

временной характер последовательности (например, в

экономических задачах). Спектральная плотность более подходит

для других типов анализа, например, при описании физических

явлений (

в частности, для анализа звука).

Вопросы этого раздела рассмотрены, например, в

[5,7,8,14,21].

2. Корреляционные функции и спектральные плотности

Пусть на входе измерительной системы действует

случайный процесс {

x(t)}, а на входе получается процесс {y(t)},

которые являются стационарными и представимы своими

реализациями

х(t) и у(t). Корреляцию между ними можно

определить, если ввести дополнительную переменную

τ

–

запаздывание

у(t) относительно х(t). По аналогии со статическим

случаем определим корреляционную функцию

х(t) и у(t) для

произвольного сдвига времени

τ

выражением:

0

() {() ()}{( ) ()}

1

lim {() ()}{ ( ) ()} ( )

xy x y

T

x

yxyxy

T

CExttyt t

xt t yt t dt R

T

τμτμ

μ

τμ τμμ

→∞

⎡⎤

⎣⎦

=− +−=

=−+−=−

∫

, (2.1)

где R

xy

(

τ

) – взаимная ковариационная функция х(t) и у(t), а

μ

x

,

μ

y

–

соответствующие средние.

()

xy

R

τ

0

1

lim ( ) ( )

T

x

tyt dt

T

τ

→∞

=+

∫

.

(2.2)

В частности, если процессы на входе и выходе одинаковы, т.е.

{y(t)}={x(t)}, то выражение (2.1) принимает вид:

2

0

1

( ) lim {() ()}{ ( ) ()} ( )

T

x

xxxxxx

T

CxttxttdtR

T

τ

μτμ τμ

→∞

=−+−=−

∫

. (2.3)

Тогда

()

xx

R

τ

0

1

lim ( ) ( )

T

x

txt dt

T

τ

→∞

=+

∫

(2.4)

называется ковариационной функцией х(t).

Иногда ковариационной функцией называют величину C

ху

,

определенную по (2.1). Поскольку R

xy

(

τ

)=С

xy

(

τ

)+

μ

x

μ

y

, то

R

xy

(

τ

)=С

xy

(

τ

), если средние обоих процессов равны нулю, т.е.

процессы центрированы. По определению ковариационная

функция является четной, т.е. R

xх

(–

τ

)=R

xх

(

τ

). Взаимная

ковариационная функция не обладает этим свойством, но

удовлетворяет соотношению: R

xy

(–

τ

)=R

yх

(

τ

).

Из соотношений (2.3), (2.4) следует, что значение

ковариационной функции в нуле равно квадрату процесса:

222

(0)

x

xxxx

R

ψ

σμ

==+. (2.5)

Если процесс центрированный, т.е.

μ

х

=0, то R

xх

(0)=

σ

х

2

, и

ковариационная функция равна дисперсии. Если

μ

х

≠0, то с

ростом

τ

ковариационная функция стремится к квадрату

среднего: R

xх

(∞)=

μ

х

2

, так как

σ

х

→0 при

τ

→∞.

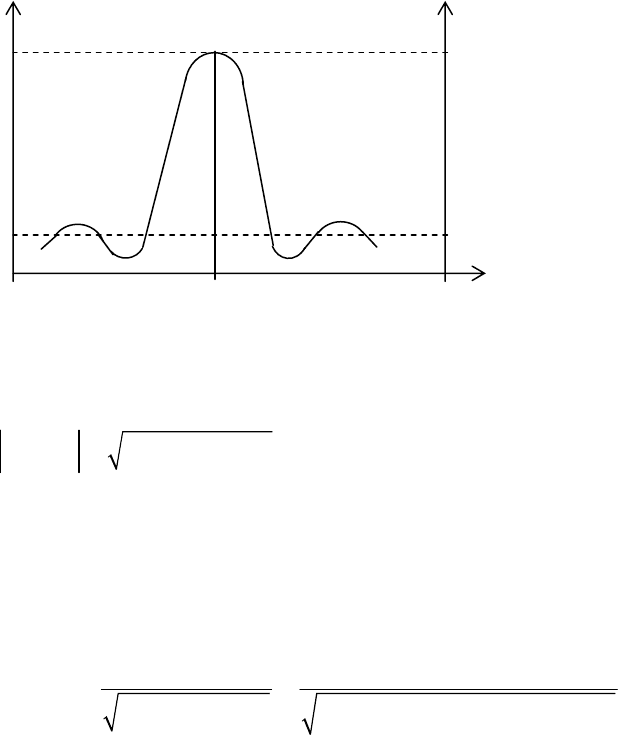
На рис.1. представлены корреляционная и ковариационная

функции.

R

xx

(τ) C

xx

(τ)

ψ

x

2

σ

x

2

μ

x

2

0

0 0 0 τ

Рис.1. Корреляционная и ковариационная функции.

Еще одним полезным соотношением является неравенство:

() (0) (0)

xy xx yy

RRR

τ

≤

, (2.6)

называемое неравенством для взаимных ковариационных

функций. Аналогичное неравенство справедливо для

корреляционных и взаимных корреляционных функций и

позволяет ввести нормированную корреляционную функцию:

22

() ()

()

(0) (0)

[(0) ][(0) ]

xy xy x y

xy

xx yy

x

xxyyy

CR

CC

RR

τ

τμμ

ρτ

μ

−

==

−−

, (2.7)

причем | ρ

xy

(τ) ≤1| для всех τ.

Как было отмечено выше, взаимная ковариационная функция,

вообще говоря, не является четной, а

R

xy

(0) не связана каким-либо

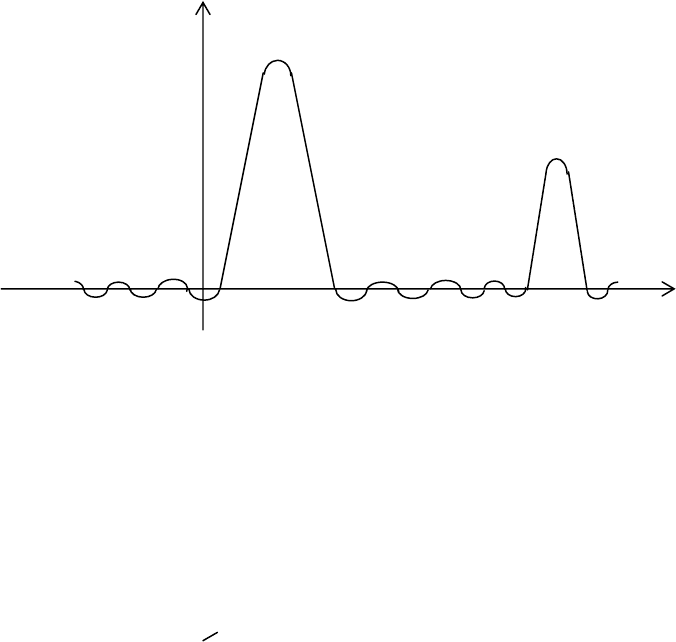
определенным образом со средним квадратом реализаций. На рис.2

представлена типичная зависимость ковариационной функции.

Спектральные плотности. Спектральную плотность можно

определить как преобразование Фурье ковариационной функции,

посредством обобщенного преобразования Фурье или

посредством аналоговой фильтрации.

R

xy

(τ)

τ

0

Рис.2. Типичная взаимная ковариационная функция.

Определение спектральной плотности через

ковариационную функцию. Пусть имеется две реализации х(t) и

y(t) стационарных эргодических случайных процессов {х(t)},

{у(t)}. Их спектральная плотность дается соотношением:

2

() ()

jf

xy xy

Sf R e d

πτ

τ

∞

−

−∞

=

∫

. (2.8)

В общем случае процессы x(t) и y(t) различны, и S

xy

называется

взаимной спектральной плотностью или взаимным спектром x(t)

и y(t). В частном случае, когда {y(t)} ={х(t)} имеем:

2

() ()

jf

xx xx

Sf R e d

πτ

τ

∞

−

−∞

=

∫

, (2.9)

где S

xх

(f) – спектральная плотность или спектр х(t). В теории

cвязи ее часто называют спектральной плотностью мощности,

автоспектральной плотностью или автоспектром.

Спектральные плотности, задаваемые выражениями (2.8) и

(2.9) определены для всех частот, как положительных, так и

отрицательных, поэтому их называют двусторонними спектрами.

Из свойств симметрии ковариационных функций следует, что

() ()

xx xx

SfSf−= , (2.10)

*

() () ()

xy xy yx

SfSfSf−= = . (2.11)

Двусторонние плотности удобны для аналитического

изучения, но практически удобнее иметь дело со спектрами,

определенными только для неотрицательных частот. Такие

плотности (или спектры) называются односторонними и задаются

соотношениями:

2

2()2 () , 0

()

0, 0

jf

xy xy

xy

Sf R e df

Gf

f

πτ

ττ

∞

−

−∞

⎧

=≥

⎪

=

⎨

⎪

<

⎩

∫

, (2.12)

2

2()2 () , 0

()

0, 0

jf

xx xx

xx

Sf R e df

Gf

f

πτ

ττ

∞

−

−∞

⎧

=≥

⎪

=

⎨

⎪

<

⎩

∫

. (2.13)

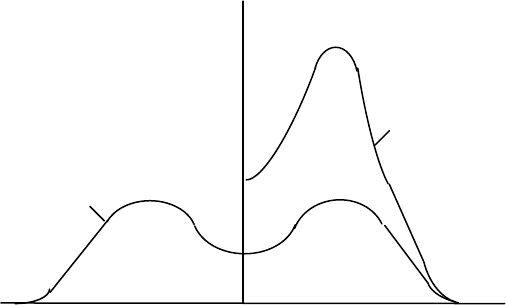
Связь между одно- и двусторонними спектрами

представлена на рис. 3.

1

2

-f 0 f

Рис.3. Односторонняя (1) и двусторонняя (2) спектральные плотности

Так как ковариационные функции являются четными

функциями τ, то, очевидно, спектры задаются только

действительной частью преобразования Фурье (2.9).

Следовательно:

0

() 2 ()cos2 4 ()cos2

xx xx xx

G

f

R

f

dR

f

d

τ

πττ τ πττ

∞∞

−∞

==

∫∫

. (2.14)

Обратное преобразование дает ковариационную функцию:

2

0

() () ()cos2

jf

xx xx xx

RS

f

ed

f

G

ff

d

f

πτ

τ

πτ

∞∞

−∞

==

∫∫

. (2.15)

Из соотношений (2.14), (2.15) получаем при τ =0:

222

0

(0) ( )

x

xxx xxx

RGfdf

ψ

σ

μ

∞

===+

∫

, (2.16)

т.е. площадь под графиком спектральной плотности равна сумме

дисперсии процесса и квадрата его среднего значения. Из

соотношений (2.3) и (2.9) получаем:

22

() () ()

jf

xx xx x

S

f

Ce d

f

πτ

ττμδ

∞

−

−∞

=+

∫

, (2.17)

т.е. ненулевое среднее входит как дельта-функция при f=0 с

масштабирующим множителем μ

x

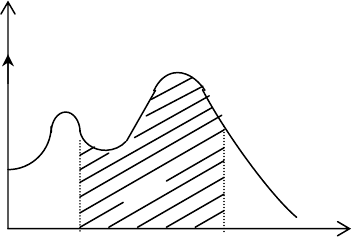
². Площадь под графиком

спектра, заключенная в интервале частот от f

1

до f

2

, равна

среднему квадрату процесса в этой полосе частот спектра (см.

рис. 4):

2

1

2

12

(, ) ()

f

xxx

f

ff

G

f

d

f

ψ

=

∫

. (2.18)

G

xx

(f)

μ

x

2

ψ

x

2

0 f

f

1

f

2

Рис.4. Свойства спектральной плотности.

Взаимная ковариационная функция R

xy

(τ) равна обратному

преобразованию Фурье двустороннего взаимного спектра S

xу

(f) из

соотношения (2.8):

2

() ( )

jf

xy xy

RS

f

ed

f

πτ

τ

∞

−∞

=

∫

. (2.19)

В случае одностроннего спектра G

xу

(f) соотношение (2.8)

принимает вид:

Романов В.Н. Теория измерений. Основы теории точности средств измерений

Подождите немного. Документ загружается.