Романов В.Н. Теория измерений. Основы теории точности средств измерений
Подождите немного. Документ загружается.

экспоненциальное распределение (для распределения Вейбулла
расчеты проводятся аналогично). Для циклических СИ имеем
λ
ц
=0,006…0,03 и P
бр
= 0,03…0,14 (при λ
а
= 0, т.е. для идеальной
аппаратуры). Для непрерывных СИ расчеты дают:
λ
н
= 0,02…0,1
и
P
бр
=0,1…0,39 (при λа = 0).
Если учесть конечную вероятность технологического брака, то
есть
р≠0, то в (4.3.5) Р
∆
≠1, и так как Р
∆
<1, то с возрастанием
технологического брака вероятность брака контроля снижается.
При больших значениях вероятности технологического брака
вообще нет смысла говорить о браке контроля, так как эта
величина более низкого порядка малости по сравнению с
технологическим браком. Учтем отказы аппаратуры контроля.
Для циклических СИ имеем (при
р=0; Р
∆
=1 и
λ
ц
=0,006…0,03):
P
бр
= 0,03…0,14 (λ
а
= 0); P
бр
= 0,17…0,28 (λ
а
= 0,03); P
бр
=0,37…0,53
(
λ
а
= 0,4), где λ
а
− интенсивность отказов аппаратуры.
Для непрерывных СИ (при
р=0; Р
∆
=1 и λ
н
=0,02÷0,1) расчеты
дают:
P
бр
=0,1…0,39 (λ
а
=0); P
бр
=0,24…0,53 (λ
а
=0,03); P
бр
=
0,46…0,72 (
λ
а
= 0,4). Расчеты проведены для периода х=5 лет
(интервал между двумя контролями). Малые значения
интенсивности отказов
λ
а
≤ 0,03 учитывают только случайную
составляющую ошибки контроля; большие значения
λ
а
≥0,4 –
систематическую.
Таким образом, для циклических СИ вероятность брака
контроля значительно ниже, чем для непрерывных; особенно это
заметно при малых интенсивностях отказов контрольно-
измерительной аппаратуры. С возрастанием интенсивности
отказов аппаратуры
λ
а
это расхождение относительно меньше.
Точность аппаратуры существенно влияет на значение
вероятности брака контроля, особенно, при малом
технологическом браке и низкой интенсивности отказов.
Определение склонности СИ к отказам. На склонность СИ к
отказам влияют режим работы и внешние условия (например,
температура, влажность, давление и т. п.). Оценим склонность к
отказам для циклических и непрерывных СИ, имеющих
различный режим работы. Используем для этого отрицательное
биномиальное распределение. Предположим, что парк
циклических и непрерывных СИ одинаков и составляет
n=100.
Будем считать успехом, если выбранный из циклических СИ
прибор откажет. Оценим вероятность того, что циклический СИ
откажет, когда в парке непрерывных СИ будет ровно
r приборов.
В этом случае одному успеху предшествует (
n
−
r) неудач.
Примем, что для циклических СИ вероятность успеха
p=0,003, а
вероятность неудачи
q=0,997; для непрерывных СИ
соответствующие величины равны:
p=0,01, q=0,99. Для
циклических СИ искомая вероятность дается выражением:
1nr nr
ц nr
PC pq
−−
−
=
(4.3.9)
Проведем расчет при r=99. В этом случае n
−
r=1, поэтому
P
ц
=0,3·10
-2
. Аналогичный расчет для непрерывных СИ при r=99
дает
P
н
=10
-2
. Последняя вероятность соответствует случаю, что
выбранный непрерывный прибор откажет, когда в парке
циклических СИ будет ровно 99 приборов. Таким образом, расчет
показывает, что склонность к отказам для циклических СИ
значительно меньше, чем для непрерывных.
Оценка вероятности отказов СИ за счет экстремальных
факторов.
В данном случае имеются в виду редкие события,
влияние которых можно оценить по распределению Пуассона.
Предположим, что редкое событие случается 1 раз в 5 лет. Тогда
параметр
m=λt в распределении Пуассона m=1. Предположим,
что вероятность числа отказов СИ из-за редкого события также
подчиняется распределению Пуассона. Примем для циклических
СИ
λ
ц
=0,0006, тогда m
ц
=λ
ц
t=0,003 (за период 5 лет), а для
непрерывных СИ
λ
н
=0,002 и m
н
=λ
н
t=0,01. Тогда суммарная
вероятность числа отказов, вызванных редкими событиями за 5
лет, определяется обобщенным распределением Пуассона. Для
циклических СИ она составляет:
P
ц
=exp(-λt)·λt·exp(-λ
ц
t)·λ
ц
t=0,0011.
Для непрерывных СИ аналогичные расчеты дают
P
н
=0,0038, т.е.
она значительно больше, чем для циклических СИ.
Повышение надежности СИ осуществляется методами
структурной и алгоритмической избыточности. В первом случае
используются схемы с дополнительными параллельно
включенными элементами, во втором – специальные алгоритмы
фильтрации помех, например, усеченное среднее, медиана и
другие, рассмотренные в § 4.2.
Вопросы, изложенные в этом разделе, рассмотрены в [1, 2, 4,
5, 8, 10, 11, 13, 15, 18, 19, 21, 22, 24, 26, 33, 34, 35, 39, 40, 47, 48].

Приложения
1. Характеристики случайных процессов
Случайный процесс. Многие физические явления
описываются функциями времени, называемыми реализациями
процесса. При изучении такого явления каждая серия измерений
дает свою реализацию, которую нельзя предсказать достаточно
точно в пределах ошибки измерений. Такие процессы и
вызывающие их явления называются случайными. Случайный
процесс {
x(t)} задается ансамблем реализаций x
i
(t) ; i=1,2….
Стационарный процесс. Средние характеристики процесса
{
x(t)}, заданного ансамблем реализаций, можно определить для
любого заданного момента времени
t
1
путем усреднения по
ансамблю. Например, среднее значение и среднее значение
квадрата процесса в момент
t
1
определяются соответственно как
11
1
1
() lim ()
N
xi
N
i
txt
N
μ
→∞
=
=
∑
, (1.1)
22
11
1
1
() lim ()
N
xi
N
i
txt
N
ψ
→∞
=
=
∑
. (1.2)
Среднее произведение значений процесса в моменты
t
1
и t
1
+τ ,
называемое ковариационной функцией при сдвиге
τ, дается
выражением:
111
1
1
(,) lim () ( )
N
xx i i
N
i
R t xtxt
N
τ
τ
→∞
=
=+
∑
. (1.3)
Аналогично определяются средние характеристики более
высокого порядка. В общем случае, когда одно или несколько
таких средних значений меняются с изменением момента
t
1
,
процесс называется нестационарным. Если же все средние не
зависят от
t
1
, то случайный процесс называется стационарным.
Средние характеристики стационарного процесса для любого
момента времени
t можно определить путем усреднения по
ансамблю реализаций только в момент
t
1.
Эргодический процесс. Средние характеристики почти
любого стационарного процесса, найденные усреднением по
ансамблю в момент
t
1
, совпадает с соответствующими средними,
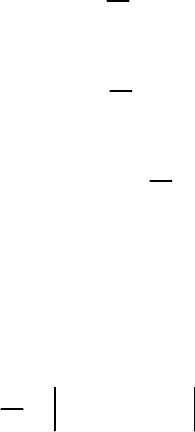
вычисленными путем усреднения по времени в пределах одной
реализации. Например, средние значения, полученные по
формулам (1.1) – (1.3), можно определить в виде:
0
1
lim ( )
T
x
T
x
tdt
T
μ
→∞
=
∫
, (1.4)
22
0
1
lim ( )
T
x
T
x
tdt
T
ψ
→∞
=
∫
, (1.5)
0
1
() lim ()( )
T
xx
T
Rxtxtdt
T
τ
τ
→∞
=+
∫
, (1.6)
где
x(t) – произвольная реализация из заданного ансамбля.
Это утверждение справедливо для эргодических систем и
составляет содержание эргодической теоремы, которая
выполняется, если удовлетворяется условие:
2
1
() 0 при
T
xx x
T
Rd T
T
τμτ
−
+→ →∞
∫
. (1.7)
Условие (1.7) является достаточным, но не необходимым
условием эргодичности. Например, на практике оно может
нарушаться, когда процесс содержит периодические
составляющие, однако и этом случае часто используют
усреднение по времени, но эти средние могут не совпадать для
различных реализаций.
На практике всегда стремятся иметь дело со стационарными
процессами, так как их
проще анализировать. Обеспечить
стационарность можно поддерживая неизменными условия
проведения эксперимента. Следует отметить, что предельные
переходы в соотношениях (1.1)–(1.6) при измерениях
практически не осуществимы, и мы всегда получаем оценки
искомых средних, а не истинные значения. Поэтому очень важно
контролировать ошибки, обусловленные конечностью объема
выборки.
Ряды и преобразования Фурье. Разложение в ряд Фурье и
преобразование Фурье имеют важное значение при анализе
случайных процессов. Ряды используются как правило для
описания периодических процессов, а преобразования Фурье –
для непериодических.
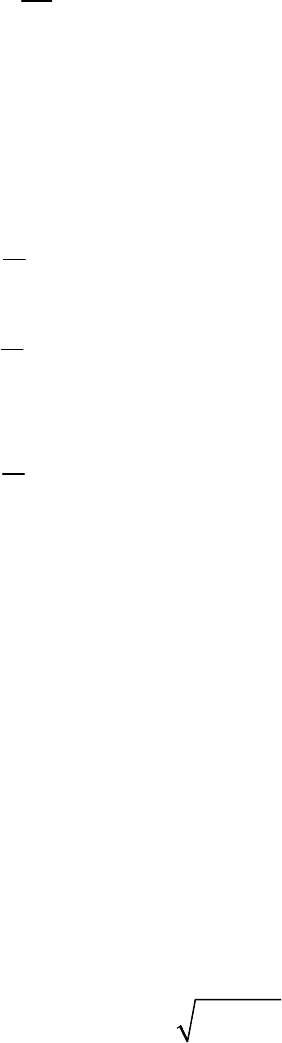
Ряды Фурье. Пусть имеется периодический процесс x(t) с
периодом
T, для которого при любом t справедливо равенство:
() ( ); 1,2,3,...
x
txtkT k=± =
. (1.8)
Фундаментальная (базовая) частота
ƒ
1
определяется выражением:
1
1/
f
T= . (1.9)
Такой периодический процесс можно разложить в ряд Фурье:
0
1
() ( cos2 sin2 )
2
kkkk
k
a
x
taftbft
ππ
∞
=
=+ +
∑
, (1.10)
где
ƒ
k
=kƒ
1
=k/T; k=1,2,3,….
Таким образом, процесс
x(t) описывается суммой синусоид и
косинусоид, частоты которых меняются дискретно с шагом
∆
ƒ=ƒ
1
. Коэффициенты a
k
, b
k
в разложении определяются
следующими выражениями:
0
2
()cos2
T
kk
axt
f
tdt
T
π
=
∫
, (1.11)
0
2
()sin2 1,2,3,...
T
kk
bxt ftdtk
T
π
==
∫
. (1.12)
В частности,
0
0
2
()
T
x
axtdt
T
μ
==
∫
, (1.13)
где
μ
x
– среднее значение процесса x(t).
В выражениях (1.11) – (1.13) циклическую частоту
ƒ
k
можно
заменить на круговую
ω
k
=2πƒ
k
, однако последняя имеет
размерность рад/с, поэтому удобнее использовать циклическую
частоту, выражаемую в герцах.
Полученные соотношения часто используют в
альтернативной форме, получаемой после несложных
преобразований:
0
1
() cos(2 )
kkk
k
xt X X ft
π
θ
∞
=
=+ −
∑
(1.14)
или
2
()
k
j
ft
k
k
xt Ae
π
∞
=−∞
=
∑
, (1.15)
где
X
0
=a
0
/2 ;
22
kkk
Xab=+, k=1,2,3,…; θ
k
=arctg(b
k
/a
k
); A
0
=a
0
/2;
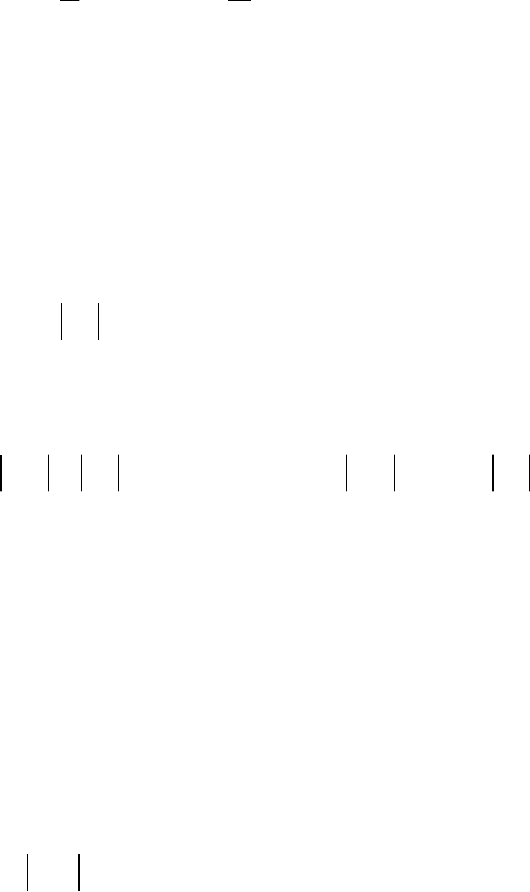
2
0
11
( ) () , 1,2,3,...
2
k
T
jft
kkk
Aajb xtedtk
T
π
−
=−= =±±±
∫
.
Последний результат вытекает из формулы Эйлера:
cos sin
j
ej
θ
θ
θ
−
=− . (1.16)
Соотношение (1.14) задает функцию x(t) в полярных
координатах (а не в прямоугольных), и на каждой дискретной
частоте
ƒ
k
она имеет модуль X
k
и аргумент θ
k
. Если функция x(t)
действительная, то её ряд Фурье можно представить в
комплексной форме. В частности для коэффициентов
A
k
имеем:
1, 2, ...
k
j
kk
AAe k
θ
−
==±±, (1.17)
где
θ
k
=arctg(b
k
/a
k
).
Если
x(t) – действительная функция t, то выполняются
равенства:
kk
A
A
−
= ,
kk
θ
θ
−
=
− ,
*
kk
jj
kk k k
A
Ae Ae A
θθ
−
−
−−
=
==, (1.18)
где * означает комплексное сопряжение.
Преобразование Фурье. Если реализация x(t) имеет
непериодический характер (переходный процесс, стационарный
случайный процесс), то рассмотренное выше представление в
виде ряда Фурье можно обобщить, переходя к пределу
Т→ ∞, что
приводит к интегралу Фурье :
2
() () ,
jft
Xf xte dt f
π
∞
−
−∞
=−∞<<∞
∫
. (1.19)
Этот интеграл существует, если выполняется условие:
()xt dt
∞
−∞
<∞
∫
. (1.20)
Функция
X(ƒ), задаваемая выражением (1.19) называется
прямым преобразованием Фурье (или спектром) функции
x(t). В
свою очередь, функция
x(t) получается путем обратного
преобразования Фурье функции X(ƒ) :
2
() ( ) ,
jft
xt X f e df t
π
∞
−∞
=−∞<<∞
∫
. (1.21)
Выражения (1.19) и (1.21) называются парой преобразований
Фурье. Следует отметить, что
X(f) в общем случае является
комплекснозначной функцией частоты, определенной на всей
действительной оси, даже в том случае, когда
x(t) –

действительная функция. Функция X(f) представима в виде
суммы действительной и мнимой частей:
() () ()
RI
Xf X f jX f=− , (1.22)
() ()cos() ()cos2
R
X
f
X
ff
xt
f
tdt
θπ
∞
−∞
==
∫
,
() ()sin() ()sin2
I
X
f
X
ff
xt
f
tdt
θπ
∞
−∞
==
∫
.
Можно также ввести представление в полярных координатах:
()
() ()
j
f
Xf Xf e
θ
−
= , (1.23)
где│
X(ƒ)│– амплитудный спектр, а θ(ƒ) – фазовый спектр.
Финитное преобразование Фурье. В действительности
реализация
x(t) стационарного случайного процесса (ССП)
наблюдается в течении конечного интервала времени
Т, которое
определяет финитное (конечное) преобразование Фурье:
2
0
() (,) ()
T
jft
T
X
f
X
f
Txtedt
π
−
==
∫
. (1.24)
При ограниченной длине реализаций ССП его финитное
преобразование существует всегда, в то время как
преобразование (1.19) может не существовать, если реализация
ССП теоретически определена при всех значениях
t, и,
следовательно, выполняется равенство:
()xt dt
∞
−∞
=∞
∫
. (1.25)
Из сравнения соотношений (1.15), (1.24) видно, что на
дискретных частотах
ƒ
k
=k/T финитное преобразование Фурье
связано с коэффициентами
A
k
ряда Фурье равенством:
(,) ; 1,2,...
kk
XfT TA k==±±. (1.26)
Отсюда следует, что если ограничиться дискретным набором
частот, то выполнение финитного преобразования Фурье (ФПФ)
сводится к расчету коэффициентов ряда Фурье для функции,
имеющей период
Т. Такие расчеты выполняются на ЭВМ по
известным процедурам.
Следует отметить, что, когда реализация
x(t) представлена
временным рядом с интервалом дискретности ∆
t, длина
реализации
Т связана с объемом выборки равенством Т=N∆t, а

частота Найквиста ƒ
c
=1/2∆t. Кроме того рассматриваемая
реализация имеет периодический характер с периодом равным
Т,
так что базовая частота ряда Фурье ƒ
1
=1/Т, и разрешающая
способность по частоте ∆ƒ=ƒ
1
. Непрерывная реализация x(t)
заменяется временным рядом
x
n
=x(n∆t), где n=1,2,…N, а
непрерывное преобразование Фурье – дискретной
последовательностью {
X
k
}={X(k∆ƒ)} k=1,2…,N. Отметим, что
погрешность дискретизации в данном случае равна нулю, так как
выполняется теорема Уиттекера [42]. Поскольку ƒ
с
=(N/2)∆ƒ, то
значения
X
k
при k>N/2 определяются по предшествующим
значениям
X
k
. Пара преобразований Фурье определяется
соотношениями:
1
( ) ( 2 ), 1, 2,...,
N
kn
n
kn
XXkf txexpj k N
N
π
=
=Δ=Δ − =
∑
, (1.27)
1
( ) ( 2 ), 1, 2,...,
N
nk
k
kn
x
x n t f X exp j n N
N
π
=
=Δ=Δ =
∑
. (1.28)
Отсюда вытекают, в частности, приведенные выше равенства,
справедливые для дискретных последовательностей {
x
n
}:
*
kk
XX
−
=
при всех k,
*
Nk k
XX
−
=
при k=1,2,…,N/2,
*
(/2) (/2)
Nk Nk
XX
+−
= при k=1,2,…,N/2,
kN k
XX
+
=
при всех k,
nN n
x
x
+
= при всех n. (1.29)
Таким образом
x
n
есть периодическая функция n по модулю N, а
X
k
–периодическая функция k по модулю N.
Дельта-функция. Рассмотрим прямоугольную функцию ƒ(t),
симметричную относительно точки
t=0, задаваемую уравнением:
1/ , / 2
()
0, / 2
t
ft
t
αα
α
⎧
≤
=
⎨
≥
⎩
. (1.30)
Площадь под ƒ(
t) равна единице :
/2
/2
1
()
S
f
tdt dt
α
α
α
∞
−∞ −
==
∫∫
. (1.31)

Пусть теперь ширина функции ƒ(t) уменьшается, а высота растет
так, чтобы сохранялась единичная площадь. Переходя к пределу
α→0 получаем дельта-функцию:
0
lim ( ) , 0
()
0, 0
f
tt
t
t
α
δ
→
=∞ =
⎧
⎪
=
⎨
≠
⎪
⎩
. (1.32)
В соответствии с уравнением (1.31) интеграл от
δ(t) равен
единице:
0
() lim 1tdt
ε
α
ε
α
δ
α
→
−
==
∫
, (1.33)
где ε>0 – произвольная малая величина. Дельта-функция может
занимать произвольное положение
t
0
на оси абсцисс, и введение
масштабирующего множителя
a дает интеграл от δ-функции,
равный
a:
0
0
0
,
()
0,
tt
att
tt
δ
∞=
⎧
−=
⎨
≠
⎩
, (1.34)
0
0
0
()
t
t
attdta
ε
ε
δ
+
−
−=
∫
. (1.35)
Свертка
δ-функции с произвольной функцией x(t) имеет вид:
00
() ( ) ( )
x
tttdtxt
δ
∞
−∞
−=
∫
, (1.36)
т.е. дает значение
x(t) при t=t
0
. Это свойство дельта-функции
можно использовать для нахождения значения
x(t) при t=t
0
. Пара
преобразований Фурье дельта-функции имеет вид:
2
() () 1,
jft
Xf te dt f
π
δ
∞
−
−∞
==−∞<<∞
∫
, (1.37)
2
() ()
jft
x
ted
f
t
π
δ
∞
−∞
==
∫
. (1.38)
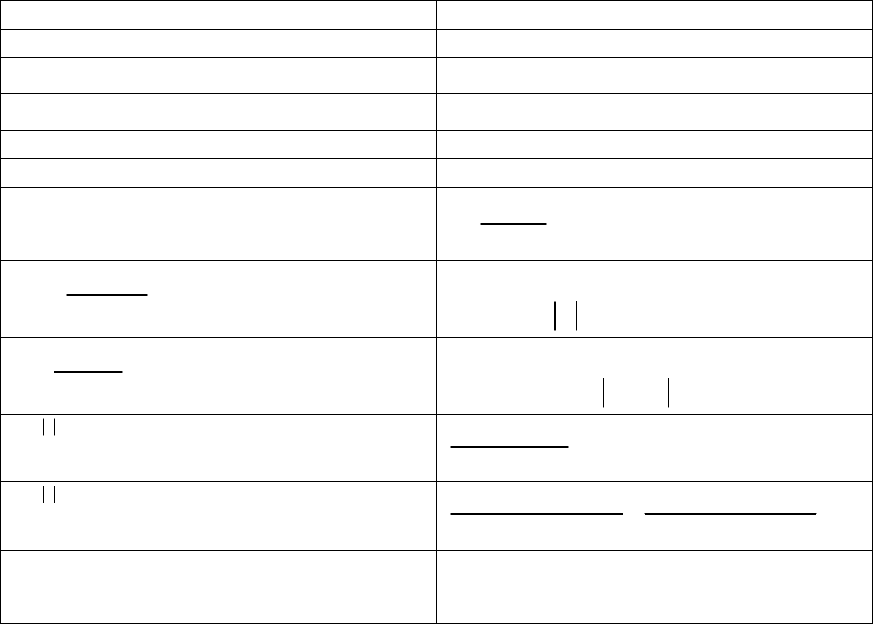
Примеры преобразований Фурье. В таблице приведены
некоторые пары преобразований Фурье, удовлетворяющие
соотношениям (1.19) и (1.21).
Примеры преобразований Фурье.
x(t) X(f)
1 δ(f)
0
2jft
e
π
δ(f–f
0
)
x(t–τ
0
)
0
2
()
jf
Xfe
π
τ
−
cos2πf
0
t [ δ(f–f
0
)+ δ(f+f
0
)]/2
sin2πf
0
t [ δ(f–f
0
) – δ(f+f
0
)]/2j
1, 0
0, 0;
tT
ttT
≤≤
⎧
⎨
<>
⎩
sin
jft
f
Te
fT
π
π
π
−
⎛⎞
⎜⎟
⎝⎠
sin 2
2
2
bt
ab
bt
π
π
⎛⎞
⎜⎟
⎝⎠
,
0,
abfb
f
b
−
≤≤
⎧
⎨
>
⎩
0
sin
cos 2
bt
ab f t
bt
π
π
π
⎛⎞
⎜⎟
⎝⎠
00
0
,/2 /2
0, / 2
afb ffb
f
fb
−≤≤+
⎧
⎨
−>
⎩
,0
at
ea
−
>
22
2
(2 )
a
af
π
+
0
cos 2 , 0
at
efta
π
−
>
22 222 2
00
4( ) 4( )
aa
affaff
ππ
+
++ +−
12
() ( )
x
ux t udu
∞
−∞
−
∫
12
() ()
X
fX f
Частотные характеристики систем. При анализе
измерительной системы предполагается обычно, что она
устойчива, имеет постоянные параметры и линейна.
Динамические свойства такой системы описываются импульсной
переходной функцией или весовой функцией, которая
представляет собой реакцию системы на входной сигнал
x(t) в
виде дельта-функции, т.е.
() () при () ()ht yt xt t
δ
==, (1.39)
причем отсчет времени
t начинается с момента подачи на вход
системы дельта-функции. В общем случае реакция
y(t) системы
