Романов В.Н. Теория измерений. Основы теории точности средств измерений
Подождите немного. Документ загружается.

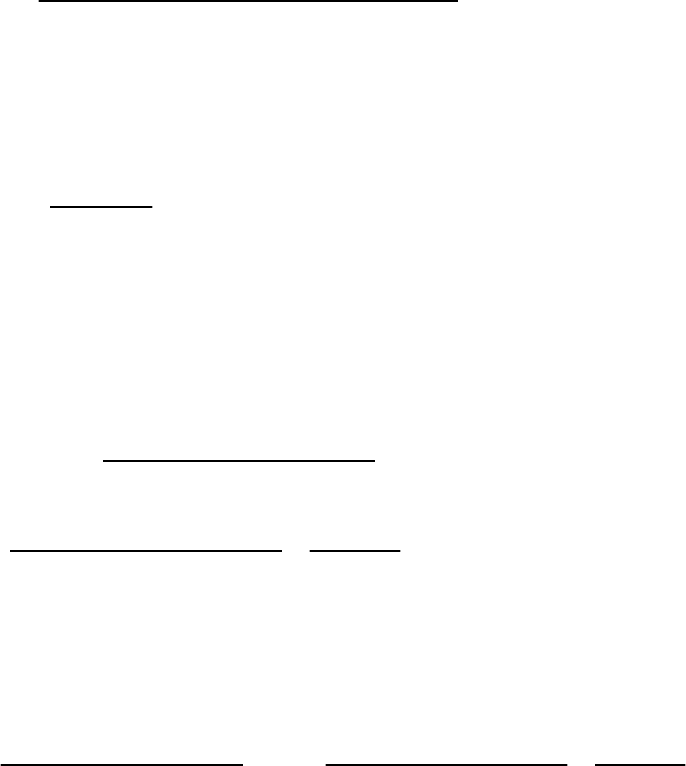
12
x
xy=− ,
22
2
[()]yfy y=+Δ,
11 01 111
()
x
aaxΔ=+
,
20212
()ya ayΔ=+. (4.1.4)
Решая систему уравнений (4.1.4) относительно y, получим
1 11 1 01 1 2 02 11
12 11 12
(1 ) (1 )
1(1)(1)
f
ax fa ffa a
y
ff a a
++− +
=
+++
(4.1.5)
Номинальное значение выходного сигнала СИ с коррекцией
равно (элементы считаются линейными)
1
2
1
1
н
f
x
y
ff
=
+
(4.1.6)
Погрешность выходного сигнала СИ с коррекцией равна (в
линейном приближении по x)
101 1202 11
12 11 12
(1 )
1(1)(1)
y н
fa f fa a
yy
ff a a
−+
Δ= − = +
+++
11
1
12 11 12 12
(1 ) 1
1(1)(1)1
a
fx
ff
aa
ff
⎡⎤
+
+−
⎢⎥
+++ +
⎣⎦
. (4.1.7)
Соотношение (4.1.7) можно упростить; оставляя только члены,
линейные по погрешностям, получим
101 1202
11
1
1 2 11 12 1 2 11 12 1 2
11
1(1 ) 1(1 )1
y
fa f f a
a
fx
ff
aa
ff
aa
ff
⎡
⎤
−
+
Δ= + −
⎢
⎥
+++ +++ +
⎣
⎦
(4.1.7а)
В последнем случае выражение для погрешности при
условии, что f
1
f
2
>> 1 и а
11
<< 1, а
12
<< 1, принимает вид

01
12 11
02
2
22
12
()
y
a
ax ax
xa
ff
ff
Δ=−−+ , (4.1.7б)
т.е. мультипликативная погрешность а
11
х может быть
существенно снижена
.
Из вида соотношения (4.1.7) следует, что мультипликативная
погрешность а
11
х мала при
1
f
f
2
→ ∞, причем аддитивная и
мультипликативная погрешности корректирующего звена а
02
,
а
12
х должны быть пренебрежимо малы. Аддитивная
составляющая а
01
при таком способе коррекции остается
существенной. Для ее уменьшения используют прием,
рассмотренный выше, а именно, вводят последовательное
корректирующее звено перед элементом СИ, так что обратная
связь охватывает оба элемента (основной и корректирующий). В
этом случае имеем следующие соотношения:
11 11
y f [x
x
=+Δ ()]
133 3
x f [x
x
=+Δ ()]
32
x x - y=
22 2
y f [y y=+Δ ()]
11 01 111
x
aaxΔ( ) = +
3 3 03 13 3
()
x
aaxΔ=+
20212
()ya ayΔ=+. (4.1.8)
Решая уравнения (4.1.8) совместно получим для выходного
сигнала с точностью до линейных по x членов следующее
выражение
A
Bx
y
C
+
=
, (4.1.9)
где А, В, С определяются соотношениями
1 01 1 3 03 11 1 3 2 02 13 11
(1 ) (1 )(1 )
A
fa ffa a fffa a a=+ +− + +,
1 3 11 13
(1 )(1 )Bff a a=++ ,
132 12 11 13
1(1)(1)(1)Cfffaaa=+ + + +
(4.1.10)

Номинальное значение сигнала на выходе равно (см. §3.1)
13
132
1
н
f
fx
y
f
ff
=
+
(4.1.11)
Погрешность выходного сигнала для СИ с коррекцией с
точностью до членов, линейных по
x, определяется выражением
13
132
1
y н
f
fx
ABx
yy
Cfff
+
Δ= − = −
+
(4.1.12)
Рассмотрим различные упрощения соотношения (4.1.12). В
реальной ситуации значения погрешностей ∆
1
, ∆
2
, ∆
3,
а
следовательно и параметров
а
0i
, а
1i
малы, т.е. а
0i
<< 1, а
1i
<< 1
(
i = 1,2,3). Оставляя только линейные по а
0i
, а
1i
члены, получим
101 1303 13202
13
132 11 12 13
1(1 )
y
fa f fa f f f a
f
fx
fff a a a
+−
Δ= + ⋅
++++
11 13
132 11 12 13 132
1
1
1(1 )1
aa
fff
aaa
fff
⎛⎞
++
⋅−
⎜⎟
+++++
⎝⎠
. (4.1.12 а)
С целью дальнейшего упрощения положим
321
fff >> 1, что
дает
01 03
3 2 11 12 13 2 11 12 13
(1 ) (1 )
y
aa
ff a a a f a a a
Δ= + −
+++ +++
02 1 3 11 13 1 3 2 12
222
11 12 13
132 11 12 13
()
1
(1 )
a
ff
xa a
fff
a
aaa
fff
aaa
+
−
−+
+++
+++
. (4.1.12 б)
Далее можно пренебречь величинами
11
a ,
12
a ,
13
a в знаменателе,
так как вклад от них следующего по погрешности порядка
малости, что дает

01 03 11 13
12
02
2
32 2 2
132
()
y
aa aax
ax
a
ff f f
fff
+
Δ= + − + − . (4.1.12 в)
Из вида выражения (4.1.12в) следует, что при данном способе
коррекции уменьшается аддитивная погрешность исходного СИ в
32
f
f раз, также оказывается уменьшенной мультипликативная
составляющая погрешности в
2
132
f
ff
раз. В этой схеме коррекции
должны быть малыми аддитивная погрешность
02
a , аддитивная
погрешность
03
a , а также мультипликативные составляющие
12
ax
и
13
ax
корректирующих звеньев.
Наряду с рассмотренными методами коррекции для повышения
точности СИ используют метод модуляции, который реализуется
двояким образом: посредством модуляции входного сигнала ()
x
t
либо посредством модуляции погрешности
()t
Δ
, вследствие чего
появляется различие в спектрах частот сигнала ()
x
t и
погрешности ()
tΔ . Модуляция сигнала производится
модулятором, устанавливаемым между источником сигнала и СИ
(в первой схеме) или между СИ и помехой (во второй схеме), а
также посредством периодического изменения параметров СИ
(например, коэффициента передачи). Исключение аддитивной
погрешности СИ осуществляется ее фильтрацией при
пропускании сигнала через фильтр верхних частот, с его
последующей демодуляцией
и применением фильтра нижних
частот [4].
Еще один метод повышения точности СИ состоит в передаче
периодических эталонных сигналов. В этом методе на вход СИ
подаются периодические эталонные сигналы
()
эт
x
t , посредством
обработки выходных сигналов определяются мультипликативные
погрешности, а затем вводятся сигналы для компенсации
погрешностей.
В рассмотренных методах модуляции и подачи периодических
сигналов основная ошибка определения погрешности СИ
обусловлена изменением ()
x
t во времени. Для повышения
точности определения
()tΔ
используется метод периодической
автоподстройки параметров. Рассмотрим этот метод в
квазистатическом режиме, когда допустимо измерение сигнала

()
x
t в дискретные моменты времени. Предположим, что функция
преобразования СИ, описывается в окрестности точки
x кусочно-
линейной моделью вида
10ii
yaxa=+, (4.1.13)
где
1i
a
,
0i
a
- случайные величины; i= 1,2,…,n.
Требуется определить значение измеряемой величины
x. Для
решения этой задачи процесс измерения выполняется в три этапа.
На первом этапе на вход СИ подается сигнал
x, на втором –
сумма сигнала x и эталонного (тестового) сигнала
эт
x
, на третьем
входной сигнал, предварительно усиленный в известное число
раз
К. В итоге получается система уравнений
11 0
21 0
31 0
;
();
;
ii
i эт i
ii
yaxa
y
axx a
yaKxa
=+
⎧
⎪
=++
⎨
⎪
=+
⎩
(4.1.14)
Ее решением является значение величины x
31
21
1
эт
yyx
x
yyK
−
=⋅
−−
, (4.1.15)
причем значение
эт
x
должно быть мало по сравнения с
диапазоном изменения величины
x, а К – не сильно отличаться
от 1. Относительная ошибка определения
x по (4.1.15) равна
31 21
1
эт
х yy yy x K
K
K
δδ δ δ δ
−−
=+++⋅
−
. (4.1.16)
Наибольший вклад в ошибку дает последнее слагаемое. Для
динамического режима автоподстройки изложенный метод имеет
ограниченную применимость, так как невозможно непрерывное
изменение
()
x
t
. СИ отключают на малую часть периода, что
вызывает появление составляющих динамической погрешности,
обусловленных прерыванием измерения
()
x
t на время
Т
Δ и
переходными процессами при включении СИ для продолжения
измерения ()
x
t .
4.2. Методы повышения помехоустойчивости СИ.
Динамические измерения. Повышение помехоустойчивости
СИ достигается в этом случае фильтрацией помех, которая
осуществляется с помощью линейных и нелинейных фильтров.
Наиболее известными линейными оптимальными фильтрами
являются фильтры Винера и Калмана.
Фильтр Винера. Пусть входной сигнал имеет вид суммы
полезного (измеряемого) сигнала и помехи:
(
)
(
)
(
)
zt xt t=+Δ
. (4.2.1)
Предполагается, что величины x (t) и
Δ
(t) являются случайными
стационарными функциями времени с известными
характеристиками. Измерения проводятся на большом интервале
времени
[]
, t−∞
. Входной процесс z(t) предполагается
центрированным, т.е. его математическое ожидание равно нулю.
Выходной сигнал СИ с фильтром определяется выражением:
()() ()()()
()
()
tt
yt ht z d ht x d
τ
ττ τ τ τ τ
−∞ −∞
=− =− +Δ
∫∫
, (4.2.2)
где
h(t-τ) - весовая функция искомого фильтра.
Погрешность фильтрации является также случайным
процессом и определяется в виде:
()
(
)
0
()et y t y t=−
(4.2.3)
где
y
0
(t)- идеальный выходной сигнал:
() ( ) ( )
00
t
y
thtxd
τ
ττ
−∞
=−
∫
, (4.2.4)
где
h
0
(t-τ) - весовая функция заданного фильтра.
Искомый фильтр характеризуется минимальным
среднеквадратичным риском, определяемым минимумом
дисперсии погрешности фильтрации:
[
]
2
0
(() ()) minDe M yt y t
⎡⎤
=−=
⎣⎦
. (4.2.5)
Выражение для
D[e] имеет вид:
[] [ ]
()
)
(
22
00
[( ( )) ] 2 ( ) ( )De M Wt MWt W t M W t
⎡
⎤
=−⋅+
⎦
⎣
. (4.2.6)

Подставляя в (4.2.6) значения y(t) из (4.2.2) и заменяя
произведение интегралов двойным интегрированием, получим:
[]
()()( )
()() ()
0
121212
0
2
tt
zz
t
zy
De ht ht R d d
ht R t d D y t
τ
τττττ
τττ
−∞ −∞
−∞
=−− − −
−− −+⎡⎤
⎣⎦
∫∫
∫
, (4.2.7)
так как
()
()
()
2
00
M
yt Dyt
⎡⎤
=⎡ ⎤
⎣⎦
⎣⎦
, где D[y
0
(t)] - дисперсия y
0
(t),
()
zz
R
τ
-
ковариационная функция входного сигнала,
(
)
0
zy
R
τ
- взаимная
ковариационная функция входного и идеального сигнала.
Таким образом, отыскание оптимальной весовой функции
искомого фильтра
()
ht
τ
− сводится к решению вариационной
задачи поиска минимума
D[e]. Её решением является
интегральное уравнение Винера-Хопфа:
()( ) ()
0
111
;
t
zz zy
ht R d R t t
τ
ττ τ τ τ
−∞
−−=−>
∫
. (4.2.8)
Физически осмысленное решение уравнения (4.2.8), как
отмечалось в §3.3, может быть получено, если известно
дифференциальное уравнение, связывающее входной сигнал
z(t) с
белым шумом. Если спектральная функция входного сигнала
()
zz
S
ω
является дробно-рациональной и её можно представить в
виде двух сомножителей
(
)
(
)
μ
ω
μ
ω
∗
⋅
, один из которых имеет
полюса в верхней полуплоскости, а второй (сопряженный) – в
нижней, то лапласовское изображение оптимальной
передаточной функции имеет вид:
()
()
(
)
()
0
0
11
2
zy
pt j t
S
hp e dt e d
p
ω
ω
ω
μπμω
∞∞
−
∗
−∞
=
∫∫
, (4.2.9)
где
()
0
zy
S
ω
- взаимная спектральная плотность входного и
идеального выходного сигналов.
В задаче фильтрации можно принять, что
(
)()
0
ht t
τ
δτ
−= −, а
полезный сигнал и помеха независимы, тогда (4.2.9) принимает
вид:
()
()
()
0
11
2
pt j t
hp e dt e d
p
ω
μ
ωω
μπ
∞∞
−
−∞
=
∫∫
. (4.2.10)
Минимум дисперсии погрешности фильтрации,
соответствующий оптимальной весовой функции, равен:

() () ( ) ( )
0
min 0
t
zy
Det Dyt ht R d
τ
ττ
−∞
=−−
⎡⎤ ⎡ ⎤
⎣⎦ ⎣ ⎦
∫
. (4.2.11)
Фильтр Калмана–Бюси. В фильтре Винера оптимальная
весовая функция получается решением интегрального уравнения,
что в реальных случаях оказывается затруднительным. Поэтому в
работе Калмана и Бюси была предложена процедура фильтрации,
основанная на решении дифференциальных уравнений с
заданными начальными условиями. При выводе уравнения
фильтра Калмана
–Бюси предполагается, что входной (полезный)
сигнал
x(t) генерируется уравнением:
() () ()
x
At x Bt qt
•
=+
(4.2.12)
где
q(t) –белый шум; А, В – матрицы.
Сигнал на выходе (результат измерения) удовлетворяет
уравнению:
() ()
zCtx t
υ
•
=+
, (4.2.13)
где
C(t) – матрица, а
()
t
υ
– белый шум.
Задача формулируется в следующем виде: по заданному
z(s),
t
0
<s<t построить оценку
(
)
1
€
x
tt
случайной функции x(t
1
), вида:
()
()()
0
11
€
,
t
t
x
tt Atsdzs=
∫
, (4.2.14)
минимизирующую дисперсию ошибки фильтрации:
[]
(
()
()
)
2
11
€
minDe M xt t xt
⎤
=−=⎡
⎣
⎦
. (4.2.15)
Как и ранее, предполагается, что процессы
x(t), q(t),
υ
(t) взаимно
независимы и центрированы, а шумы имеют корреляционные
функции вида:
() ( ) () ( )
Mqtq Qt t
τ
δτ
=−
⎡⎤
⎣⎦
() ( ) () ( )
Mt Rtt
υ
υτ δ τ
=−
⎡⎤
⎣⎦
, (4.2.16)
где
Q(t), R(t) – соответствующие ковариационные матрицы,
()
t
δ
τ
− – дельта-функция Дирака.
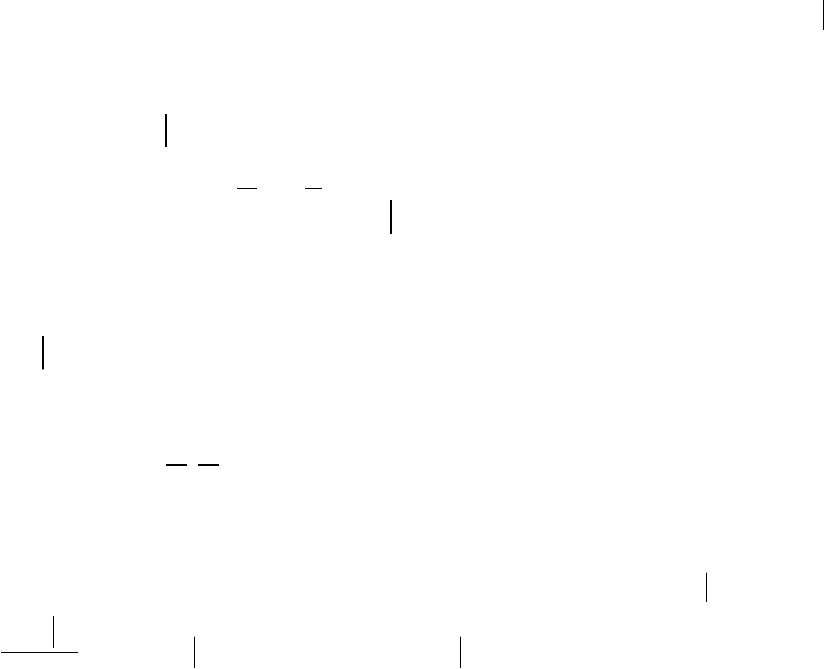
Необходимым и достаточным условием того, чтобы
()
1
€
x
tt
было решением задачи фильтрации, является выполнение
уравнения Винера–Хопфа:
()
() ()
()
11
€
() ( ) 0Mxt xtt z z
στ
⎡⎤
−−=
⎣⎦
(4.2.17)
для всех
σ
и
τ,
t
0
<
τ<σ<
t. Или что то же:
(
)
(
)
(
(
)
)
(
)
(
)
(
(
)
)
11
€
0Mxt z z Mxtt z z
στ στ
⎡⎤
⎤
−
−−=
⎡
⎣
⎦
⎣⎦
. (4.2.17а)
При сделанных предположениях справедлива следующая
теорема. Пусть для задачи фильтрации существует решение вида:
()
()()
0
€
,
t
t
x
tt htsdz s=
∫
, (4.2.18)
где
h(t, s) – весовая функция, непрерывно дифференцируемая по
t, тогда для t
0
<s<t справедливо соотношение:
( ) () ( ) ( ) () ( )
,,,,hts Athts httCthts
•
=−
. (4.2.19)
Следствием теоремы (4.2.19) является дифференциальное
уравнение, которому должно удовлетворять оценка
()
€
x
tt
:
()
()
()
() () ()
()
€
€€
[]
dx t t
A
txtt Kt zt Ctxtt
dt
=+−
, (4.2.20)
где
() ( ) () ()
(
)
(
)
[
]
1
€
,;()KthttPtCtRtPtDxt
∗−
≡= = – ковариационная
матрица, которая является решением уравнения типа Риккати:
() () () () () () () ()
1
P
At P PA t PC t R tCt P BtQt B t
•
∗∗− ∗
=+− +
(4.2.21)
с начальными условиями
P(t)=P
0
=D[x
0
].
Уравнение (4.2.20) определяет структуру оптимального
линейного фильтра. Практическая реализация фильтров Винера и
Калмана связана с рядом технических трудностей, поэтому на
практике применяются фильтры на основе
RC-цепочек и
операционных усилителей, являющиеся субоптимальными,
однако более легко реализуемыми. Фильтры Калмана получили
распространение при фильтрации дискретных
последовательностей. Рассмотрим примеры использования
линейных фильтров.
Пример 1. Определим одномерный фильтр с полосой
пропускания 2
Δ, центрированной на частоте f
0
. Его частотная
характеристика имеет вид:

()
0
П
1 для
0 впротивном случае
ff
Hf
±≤Δ
⎧
=
⎨
⎩
. (4.2.22)
Такой фильтр называется полосовым. Обычно
Δ считается малой
величиной. Если
f
0
=0, то фильтр называется низкочастотным.
Если на вход такого фильтра подается сигнал в виде ряда:
() ( )
1
cos 2
n
ii
i
i
xt fa
π
θ
=
=+
∑
, (4.2.23)
то на выходе получается ряд:
(
)
(
)
0
cos 2
i
iii
ff
yt fa
π
θ
≤±Δ
=+
∑
, (4.2.24)
где суммирование ведется по всем
i, удовлетворяющим
неравенству
0i
ff±≤Δ
. Таким образом, составляющие x(t),
частоты которых близки к
f
0
, остаются без изменений, а другие
составляющие при фильтрации устраняются.
Пример 2. Второй важный для приложений фильтр
определятся преобразованием Гильберта. Его частотная функция
имеет вид:
()
Г
при 0
0 при 0
при 0
if
f
if
Hf
−>
=
<
⎧
⎪
=
⎨
⎪
⎩
. (4.2.25)
Если на вход такого фильтра подается сигнал
x(t), определяемый
выражением (4.2.23), то на выходе получается сигнал:
() ( )
1
sin 2
n
ii
i
i
yt fta
π
θ
=
=+
∑
, (4.2.26)
т.е. применение такого фильтра сдвигает входной сигнал по фазе
на
π
/2. Отметим интересную связь преобразования Гильберта со
свойством осуществимости линейной системы с постоянными
параметрами. Линейная система физически осуществима тогда и
только тогда, когда
H
I
(f) есть преобразование Гильберта H
R
(f), т.е.
H
I
(f)=H
Г
H
R
(f), где H
I
,
H
R
– мнимая и действительная части
частотной характеристики системы
H(f): H(f)=H
R
(f)-jH
I
(f),
определяемые из соотношений:
() ()
0
cos 2
R
H
fh fd
τ
πττ
∞
=
∫
