Романов В.Н. Теория измерений. Основы теории точности средств измерений

Подождите немного. Документ загружается.

(2 ) (2 )

ggb

Сигналы вида (3.1.48) с выходов нейронов второго слоя

подаются на вход каждого нейрона третьего слоя. Выражение для

сигнала на выходе нейрона r третьего слоя получается из

соотношений типа (3.1.42а – 3.1.47) с заменой индексов и

обозначений (1j)→(3r); n→p;

ac→ ;

z→ ;

(1 ) (3 )

kk→

. В

итоге получаем

(3 )

(3 ) (3 )

1 exp( )

()

() supmin(1, ())

μω

−

+−

= , (3.1.49)

где r =1,…,l;

(3 ) (3 )

(1 ex p( ))

vkg

−

=+ − ;

(3 )

...

gcz cz=++ ;

(3 ) (3 )

ggc

+= .

Выражение (3.1.49) позволяет определить сигнал на выходе

нейронной сети (результат измерения) и его неопределенность,

зависящую от неопределенности нечетких входных сигналов и

нечетких параметров сети. Достоверность результата измерения

(3.1.49) определяется сравнением с индексом нечеткости

множества

v . Результат считается достоверным, если

()

> .

Таким образом, в случае четких входных сигналов

погрешность сигнала на выходе любого нейрона третьего слоя

сети (погрешность результата измерения) зависит от выходных

сигналов (и их погрешностей) всех нейронов предыдущих слоев.

В нечетком случае функция принадлежности, характеризующая

выходной сигнал и его неопределенность, зависит от функций

принадлежности выходных сигналов нейронов предыдущих

слоев

3.2. Метрологический синтез

Под метрологическим синтезом понимается построение

структурной схемы СИ, удовлетворяющей заданным критериям

(показателям), то есть синтез представляет собой задачу

многокритериальной оптимизации. Как правило, используются

следующие группы критериев: функциональные критерии, к

которым относятся точность измерений, диапазон,

производительность (число измерений в единицу времени),

универсальность (число измеряемых величин) и т.п.; технико-

экономические,

к которым относятся стоимость, эксплуатационные

расходы, надежность, долговечность и т.п.; эргономические

критерии, отражающие удобство для пользователя, например,

безопасность, удобство эксплуатации, простота эксплуатации и

обслуживания, дизайн и т.д.. В ряде случаев применяются

дополнительные критерии, связанные с конкретными условиями

функционирования, например, степень автоматизации,

помехозащищенность, габариты, и т.д. Обозначим

K -

критерии;

nj ,...,2,1= . Достижимые значения критериев зависят

прежде всего от типа схемы

T и числа входов-выходов N, так что

выбор оптимальной схемы определяется выражением:

(

)

()

max ,arg

SKTN

∈Σ

= . (3.2.1)

Здесь K

(S)

– общий критерий, характеризующий систему (структуру

S), получаемый сверткой частных критериев

K :

()

(

)

(

)

NTKFK

,= ,

где F – операция свертки (агрегирования) по критериям

K .

Часто задачу оптимизации заменяют задачей обеспечения, когда

значения критериев не должны быть меньше некоторых допустимых

значений:

(

)

(

)

{

}

KNTKSS ≥Σ∈= , (3.2.1а)

где

K – допустимое значение j-го критерия, Σ – множество

допустимых систем.

В общем виде задача многокритериальной оптимизации вида

(3.2.1) не поддается конструктивной формализации, декомпозиции, и

однозначному решению, поэтому используют различные упрощения.

Одним из распространенных подходов является применение

эвристического метода. Он состоит в том, что лицо принимающее

решение (ЛПР), например, проектировщик, на основе информации о

предметной области формирует исходное множество допустимых

решений (допустимых

структур СИ). На втором этапе методом

перебора строится множество Парето- решений (эффективных

решений), каждое из которых имеет максимальное возможное

значение хотя бы одного критерия. На этом этапе исследуются

предельные возможности различных типов схем по заданным

критериям. Затем из множества эффективных решений определяется

наилучшее возможное решение, являющееся субоптимальным.

Построение множества Парето и

выбор субоптимального решения

осуществляется ЛПР непосредственно или в режиме интерактивного

диалога с ЭВМ. Обычно субоптимальных решений оказывается

несколько, поэтому для получения однозначного решения

используют дополнительные условия, например, минимизация

стоимости, максимизация надежности и т.п. Многокритериальную

задачу можно упростить, если её условия позволяют определить

главный критерий. Для СИ в качестве главного

критерия часто

используется какая-то характеристика точности измерений. В этом

случае задача синтеза становится однокритериальной при

дополнительных ограничениях по другим критериям; ее решение

может быть получено известными методами, например, методом

множителей Лагранжа. Для сведения многокритериальной задачи к

однокритериальной кроме метода главного критерия используются

также метод свертки, метод пороговых критериев, метод расстояния

[41]. После того как решена задача структурного синтеза, решается

задача параметрического синтеза, то есть выбора параметров

элементов схемы, структура которой фиксирована. При этом

считаются известными также условия эксплуатации и технология

изготовления. Рассмотрим постановку задачи параметрического

синтеза для нескольких характерных случаев.

Минимизация стоимости СИ. Обозначим

– номинальные

значения параметров;

– технологические допуски для

соответствующих параметров;

mj ,...,2,1

, где

– число

параметров;

c – стоимость изготовления i -го элемента по

параметру

()

ijj

cy=Δ. Положим для простоты, что каждый

элемент характеризуется одним точностным параметром. Будем

также считать, что номинальные значения определены, тогда

используя аддитивную свертку, наилучшее решение можно

записать в виде решения, минимизирующего среднюю

взвешенную стоимость СИ:

()

,arg min

ii j j

pc y

Δ∈

∈

Δ= Δ

∑

, (3.2.2)

где

– важность (вес) i -го элемента;

– области задания

номинальных значений и допусков соответственно. В более

общем случае решение записывается в виде:

(

)

(

)

,arg min

ii j j

Fpc y

Δ∈

∈

Δ= Δ , (3.2.2а)

где F – функция (функционал) усреднения по индексу

i ,

зависящая от структурной схемы и условий задачи.

Как правило вводится дополнительное условие по

надежности, чтобы решение было однозначным и приемлемым:

(

)

допt

PyP ≥Δ

, , (3.2.3)

где

P – вероятность безотказной работы в течение времени t ;

доп

P –

допустимое значение вероятности безотказной работы;

y – вектор

номинальных значений параметров для оптимального решения.

Максимизация надежности СИ. Вторая альтернативная

постановка задачи связана с максимизацией надежности при

ограничении по стоимости СИ. В тех же обозначения имеем:

(

)

(

)

,arg max

iti j j

FpP y

Δ∈

∈

Δ= Δ , (3.2.4)

при условии

(

)

доп

с ycΔ≤ , где

доп

c – допустимое значение стоимости

СИ; F – функция (функционал), определяемая типом структурной

схемы.

Решение задач (3.2.2.), (3.2.4.) может быть получено

численными методами в режиме интерактивного диалога с ЭВМ

[6, 10, 41], при этом ЛПР задает желаемые значения запаса по

стоимости (надежности) по каждому параметру, исходя из

некоторого приближения, а затем корректирует значения

параметров по результатам расчета

на ЭВМ. Для типовых схем,

рассмотренных в §3.1, задача оптимизации по одному

функциональному критерию, например по критерию точности,

может быть решена в явном виде. Рассмотрим примеры.

Пример 1. Пусть требуется минимизировать погрешность

преобразования

пр

yΔ . В качестве критерия можно использовать

среднее значение модуля ошибки или средний квадрат ошибки. В

последнем случае критерий оптимизации имеет вид:

{}

()()

{}

max

min

пр i

yMfxfxdx

⎡⎤

Δ= −

⎡⎤

⎣⎦

∫

, (3.2.5)

где

– параметры СИ данного типа. Так как

[]

ffM = , то

выражение (3.2.5) принимает вид:

{}

() ()

{}

max

min

пр i

yMfxfxdx

⎡⎤

Δ= −⎡⎤

⎣⎦

∫

. (3.2.6)

Минимизация выражения (3.2.6) позволяет найти значения

параметров

, соответствующие предельному значению

погрешности преобразования.

Пример 2. Пусть требуется минимизировать дисперсию

случайной погрешности измерений для СИ данного типа. Решение

этой задачи зависит от структурной схемы СИ.

Последовательная схема. Воспользуемся выражением (3.1.7)

для дисперсии погрешности:

[] [] []

min

Dy SDx SDx

Δ= Δ= Δ→

∏

, (3.2.7)

где

S – заданная чувствительность схемы.

Из (3.2.7) следует, что уменьшить дисперсию погрешности

измерений можно за счет уменьшения дисперсии входного

сигнала и чувствительности схемы. Наибольший вклад в

изменение дисперсии погрешности вносят элементы с малой

чувствительностью. При минимизации дисперсии относительной

погрешности сигнала на выходе используем выражение (3.1.12) в

линейном приближении:

[] []

min

Df Dxa

δδ

+→

∑

(3.2.8)

при дополнительном условии

∏

, где a – коэффициент,

зависящий от параметров схемы (a=1, если f

– постоянные

величины)

f – заданная функция преобразования.

Из соотношения (3.2.8) следует, что уменьшить дисперсию

можно, уменьшая дисперсию погрешности преобразования

отдельных элементов и сокращая число элементов схемы.

Параллельная схема. Из выражения (3.1.13) имеем для

дисперсии погрешности:

[] [] []

Dy S Dx SDx

⎛⎞

Δ= Δ= Δ

⎜⎟

⎝⎠

∑

. (3.2.9)

Из (3.2.9) следует, что наибольший вклад в изменение

дисперсии вносят элементы с большой чувствительностью.

При минимизации дисперсии относительной погрешности из

(3.1.20) в линейном приближении имеем:

[] []

min

ii i

Dff f Dxa

δδ

⎛⎞

⋅+→

⎜⎟

⎝⎠

∑∑

, (3.2.10)

при дополнительном условии

∑

, где a – коэффициент,

зависящий от параметров схемы (a=1, если

– постоянные

величины).

Используя метод множителей Лагранжа и приравнивая к

нулю частные производные по

, получим после несложных

преобразований, что минимум дисперсии достигается при

fff === K

и соответственно

[

]

(

)

D f const i

= , т.е. при одинаковой

дисперсии функций преобразования элементов схемы:

[] [] []

min

Dy Df Dx

δδ

=+. (3.2.11)

Таким образом, в параллельной схеме составляющая

дисперсии относительной погрешности за счет погрешности

преобразования отдельных элементов уменьшается в k раз. Не

следует забывать, однако, что при этом может увеличиваться

дисперсия абсолютной погрешности, обусловленная

погрешностью входного сигнала.

Аналогично можно рассмотреть и другие типы схем. Так для

схемы с обратной связью имеем из

(3.1.26):

[]

[

]

12 2

(1 )

SD x

f signf

Δ=

−

. (3.2.12)

Результат для этого случая аналогичен параллельной схеме,

т.е. уменьшением чувствительности прямой и обратной ветви, а

также дисперсии погрешности входного сигнала можно

уменьшить дисперсию абсолютной погрешности измерения.

При минимизации дисперсии относительной погрешности

выходного сигнала для схемы с обратной связью из соотношения

(3.1.30) при дополнительном условии

()

2211

1 fsignffff −

получим результат, аналогичный случаю параллельной схемы с

двумя элементами. В частности, условие минимума дисперсии

имеет вид

221

−

fsignff . (3.2.13)

С другой стороны, при выполнении соотношения (3.2.13)

справедливо равенство

[]

[

]

fDfD

, как для параллельной схемы

при k=2. При положительной обратной связи условие минимума

может быть обеспечено лишь при

DD .

В ряде случаев необходимо иметь информацию о

вероятностных характеристиках погрешности, в качестве которых

используются доверительный интервал и доверительная

вероятность. Выберем за критерий оптимизации доверительный

интервал, в который с заданной вероятностью попадает значение

погрешности

{}()()

2Ppdpd

αα

δα δδ δδ

−

−≤ ≤ = =

∫∫

, (3.2.14)

где

()

p - плотность вероятности распределения погрешности;

причем математическое ожидание погрешности равно нулю.

Последовательная схема. Предположим, что погрешности

элементов схемы

независимы и одинаково распределены.

Рассмотрим два практически важных случая: нормальное и

равномерное распределение погрешностей

для элементов

схемы.

Нормальное распределение. Так как относительная

погрешность выходного сигнала

равна сумме погрешностей

элементов схемы (см. соотношение (3.1.9)), то из центральной

предельной теоремы следует, что

имеет также нормальное

распределение с математическим ожиданием и дисперсией,

определяемыми по (3.1.11) и (3.1.12) соответственно. Тогда

вероятность попадания погрешности

в заданный интервал при

достаточно большом k дается выражением

[] [] []

()

PM y y M y t D y t

δδ δ δ

≤≤ + =Φ−Φ, (3.2.15)

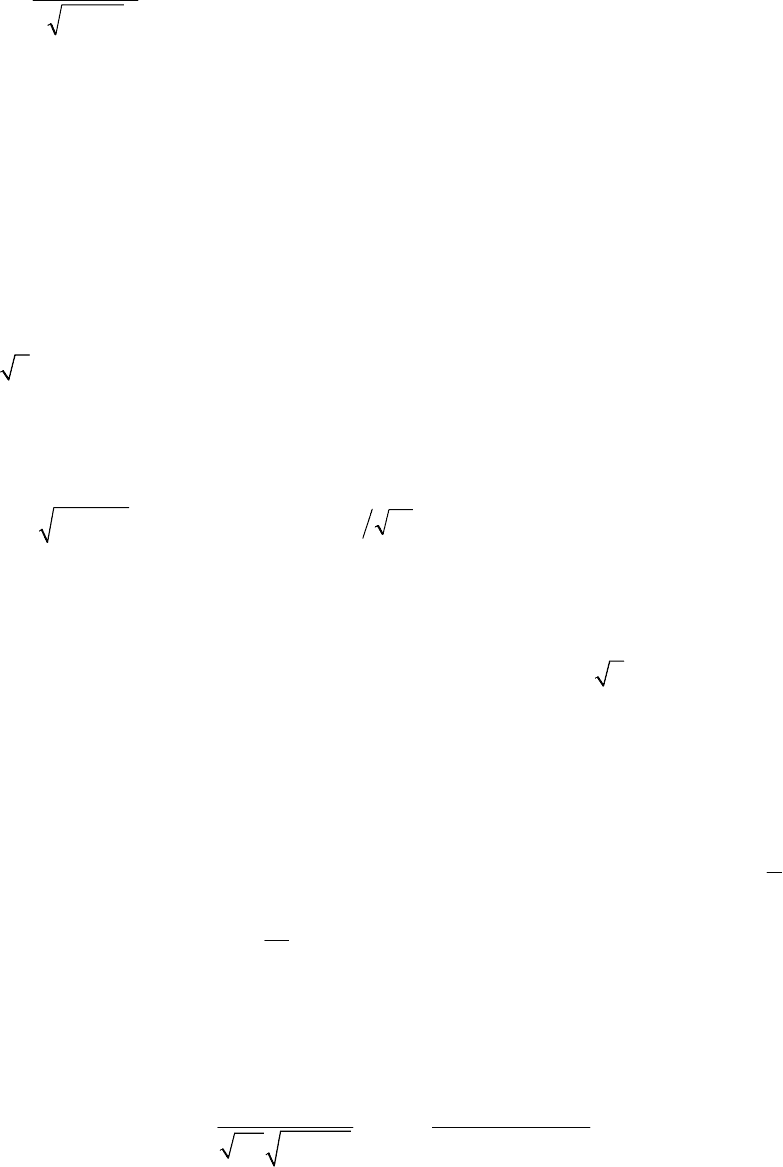
где

()

,tΦ

Φ – значения функции нормального распределения,

определяемые по таблицам;

t –безразмерный параметр:

[]

−

Так, например, при

t вероятность попадания

соответствующий интервал

(

)

2 0,98 0,5 0,48Pt== − = ;

при

3t = :

()

3 0,999 0,5 0, 499Pt== − = . Следует отметить, что мы

выбрали половину симметричного интервала относительно

математического ожидания. Если принять, что

[

]

()

f const i

= и

[

]

()

D f const i

= , т.е. все элементы схемы в статистическом смысле

эквивалентны, то из полученных выше соотношений (3.1.11,

3.1.12, 3.2.15) следует, что доверительный интервал возрастает в

k раз по сравнению с одним элементом. Положим

10k =

, т.е. в

схеме объединены 10 элементов, и

[

]

, тогда доверительная

вероятность попадания величины

в тот же доверительный

интервал, что и для отдельного элемента при

, т.е. в интервал

[]

tD f

⎡⎤

⎣⎦

, составит:

(

)

23,05,073,0102 =−==tP , т.е. всего 23%

(против 50% для отдельного элемента). Таким образом,

последовательная схема статистически менее надежна, или при

той же доверительной вероятности, что и для отдельного

элемента, точность функционирования ниже в

k раз.

Равномерное распределение. В этом случае, если погрешность

для i-го элемента схемы изменяется в пределах

[

]

,0 , то для схемы

из k элементов

будет заключено в интервале

⎥

⎦

⎤

⎢

⎣

⎡

∑

. Отсюда

следует, что математическое ожидание равно:

[]

∑

;

дисперсия

[]

∑

. Вид распределения величины

зависит от k. Так при k=2 получается треугольное распределение.

При большом k (практически, при k>5) распределение

приближается к нормальному с функцией плотности:

()

[]

(

)

[]

exp

yM y

δδ

πδ

⎧

⎫

−

⎪

=⋅−

⎨

⎬

⎪

⎩⎭

. (3.2.16)

Вероятность попадания

в заданный интервал

рассчитывается аналогично случаю нормального распределения из

соотношения (3.2.15). Для произвольного k плотность

нормированного распределения суммы k равномерно

распределенных величин имеет вид

()

12 2 12

kk k

py f y

δδ

⎛⎞

⎜⎟

⎝⎠

, (3.2.17)

()

() ( )

[]

K+−+−−

−

−−

−

xCxCx

xf , (3.2.18)

где 0<x<k, а суммирование продолжается до тех пор, пока

аргументы

,1,2,xx x−−

…K остаются положительными.

Вероятность попадания

в заданный интервал, например [0, α]

рассчитывается при малых k непосредственно

{}()

0Py pydy

αδδ

≤≤=

∫

, (3.2.19)

где

()

дается соотношением (3.2.17).

Параллельная схема. Рассмотрение проводится аналогично

случаю последовательной схемы с тем различием, что мы имеем

взвешенную сумму независимых случайных величин. Положим

для простоты

[

]

(

)

f const i

= ,

[

]

(

)

D f const i

= ,

(

)

iconstf

= .

Используя соотношения (3.1.19, 3.1.20), найдем, что вероятность

попадания y

в интервал

[] [] []

ii i

fMf Df

δδ δ

⎛⎞

⎜⎟

⎝⎠

равна для

нормального распределения величин

()

20,48;Pt==

()

3 0,499Pt== . Однако при той же вероятности ширина

доверительного интервала будет в

k раз меньше, чем для

отдельного элемента схемы. Вероятность попадания погрешности

для схемы из 10 элементов в тот же доверительный интервал, что

и для отдельного элемента схемы равна:

[]

{

}

()

0, 2 2 10 1 0, 5 0,5

Py kDf Pt

δδ

⎡⎤

∈===−=

⎣⎦

, в то же время для

отдельного элемента она равна 0,48. При небольшом числе

элементов, например, при k=2:

(

)

497,05,0997,022 =−==tP .

Таким образом, для параллельной схемы обеспечивается

более высокая статистическая надежность результата измерения,

чем для отдельного элемента, при той же точности

функционирования. Отметим, что этот вывод получен при учете

влияния только погрешностей функций преобразования

отдельных элементов, распределенных по нормальному закону.

Схема с обратной связью. Результаты для нее аналогичны

параллельной схеме при k=2.

Выведем соотношения между доверительным интервалом и

вероятностью для равномерного распределения при k=2 и k=3.

При k=2 сумма двух равномерно распределенных величин, каждая

из которых распределена симметрично в интервале

[]

,− , имеет

треугольное распределение с функцией плотности:

()

[]

0; 2 , 2 ,

;2 0,

;0 2 .

px x

αα

⎧

⎪

∉−

⎪

=+ −≤≤

⎨

⎪

−≤≤

⎪

⎩

(3.2.20)

Центр распределения помещен в нуле, а интервал изменения

переменной

[]

2,2: −x

. Вероятность попадания погрешности в

интервал

[]

ΔΔ− , определяется из соотношения:

{}()

Py pydy

δδ

−Δ

−Δ ≤ ≤ Δ =

∫

. (3.2.21)

Подставляя

()

из (3.2.20) и проводя интегрирование,

найдем:

{}

⎛⎞

−Δ ≤ ≤ Δ = ⋅ −

⎜⎟

⎝⎠

. (3.2.22)

Математическое ожидание величины

[

]

0My

= , так как

мы рассматриваем симметричное распределение относительно

нуля.

Если центр распределения поместить в произвольной точке c,

то

[

]

= , однако это не сказывается на дальнейших

результатах. Дисперсия

[]

. Напомним, что для

равномерного распределения в интервале

[

]

−

дисперсия равна:

[

]

/3Dy

δα

= .