Романов В.Н. Теория измерений. Основы теории точности средств измерений
Подождите немного. Документ загружается.


[]
2
2
11
/
kk
iii
ii
Dfx f f
δδ
==
⎛⎞
+
⎜⎟
⎝⎠
∑∑
(3.1.20а)
Если положить
(
)
i
f
const i= и δx=0, то имеем:
[] [ ]
i
M
yMf
δ
δ
= , (3.1.19б)
[]1/[ ]
i
Dy kDf
δ
δ
= . (3.1.20б)
Из полученных соотношений следует, что математическое
ожидание погрешности не изменяется, а составляющая
дисперсии, зависящая от погрешности преобразования
уменьшается в k раз по сравнению с дисперсией относительной
погрешности для отдельного элемента схемы.
Схема на рис.13,в сводится к нескольким схемам,
представленным на рис.13,а, так что получаем систему
уравнений
для определения погрешности выходной величины.
При этом функции f
(1)
,…,f
(k)
могут содержать несколько
составляющих, что не принципиально. Для погрешностей
выходных величин каждой ветви справедливы соотношения
(3.1.1) – (3.1.7). Например, выражение (3.1.2) запишется в виде:
()
∏
=
Δ=Δ
j
k
i
j
i
j
xSy
1
)(
, (3.1.21)
где
j
-номер ветви, lj ,1= ;
j
k - число элементов в −
j
ой ветви
схемы.
Схема на рис.13,г сводится к схеме на рис.13,б с учетом того,
что сигналы на входе каждой ветви различны. При этом, как и в
предыдущем случае, каждая ветвь может состоять из
последовательных или параллельных элементов. Считая, что
операторы
f в каждой ветви простые (не составные), получим
из (3.1.13а)
() () () ()
j
l
j
jj
l
j
j
fxxSy Δ+Δ=Δ
∑∑
== 11
)1(
, (3.1.22)
где
−l число ветвей.
В квадратичном приближении имеем соотношение,
аналогичное (3.1.13б)
() ()
(2) (1)
1
l
jj
j
y
yfx
=
Δ=Δ+ΔΔ
∑
, (3.1.22а)
где
)1(
yΔ - определяется из соотношения (3.1.22)
Аналогично могут быть записаны и другие соотношения
для данной схемы.
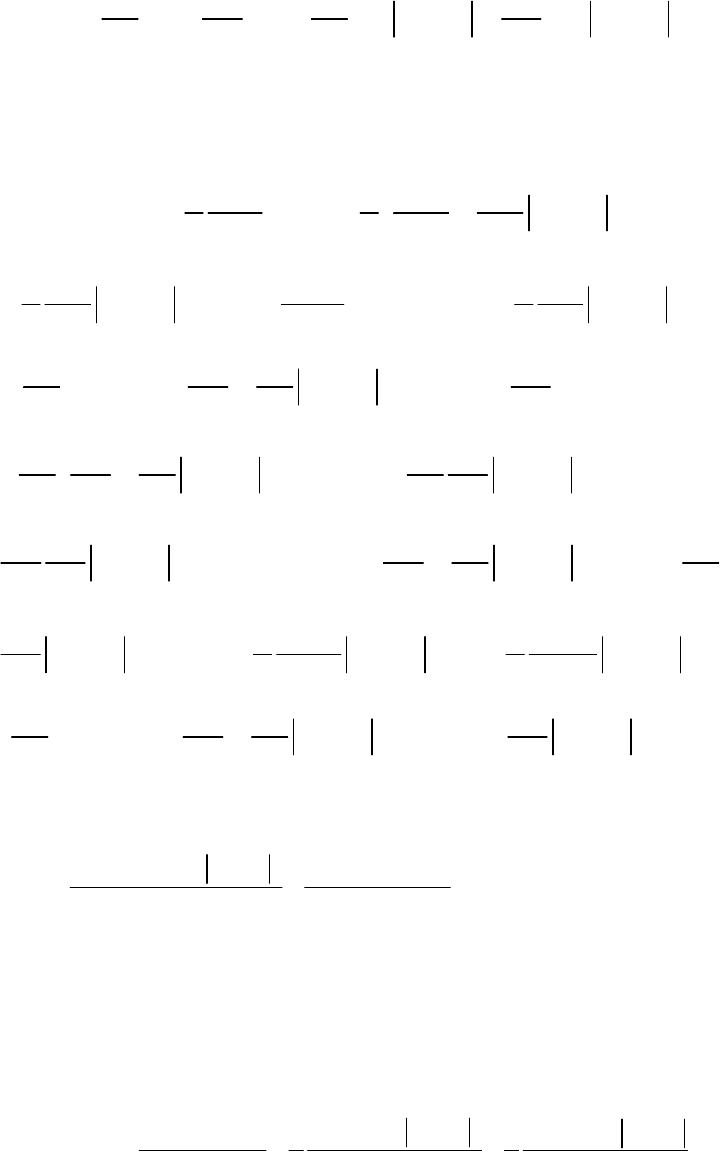
Для схемы на рис.13,д в линейном приближении можно записать
(1)
11
112 22
11 2
/
fy
zz
y x f f signf f signf Q
xf f f
⎛⎞
∂∂
∂∂
Δ= Δ+ Δ+Δ + Δ
⎜⎟
∂∂ ∂ ∂
⎝⎠
,
где Q=(1–∂z/∂y⋅signf
2
); y
1
=f
1
(x); z=f
1
(f
2
(y)); y–f
1
(f
2
(y))⋅signf
2
=f
1
(x);
∂z/∂y=(∂f
1
/∂f
2
)(∂f
2
/∂y). В квадратичном приближении получаем для
погрешности при произвольных функциях преобразования
22
2
(2) (1) 2 2
11
21
222
11
2
22
2
1
22 1 2
22
21
11
{()( )()
22
11
() ( )}/
22
fy
z
y y x signf f
xff
y
zz
signf f f x Q signf
ffxy
∂∂
∂
Δ=Δ+ Δ+ + Δ+
∂∂∂
∂
∂∂
+Δ+ΔΔ+⋅
∂∂∂∂
22 2 2 2 2
11
21 2
11 2
11 1
21 22
11 2
32
111
212 2 1 1
12 1 1
2
2
{( )( ) ( )( ) ( )( )
2( )( )2 ( )
()}/{( )() ()
(
fy
zz
x signf f f
xff f
fy f
zz
signf x f signf x f
xf f xf
yyf
zz
s
ignf f f Q signf f f x
ff f f x
z
signf
f
∂∂
∂∂
Δ+ + Δ + Δ +
∂∂∂ ∂
∂∂ ∂
∂∂
+ΔΔ+ ΔΔ+
∂∂ ∂ ∂∂
∂∂∂
∂∂
Δ
Δ++ Δ+ΔΔ+
∂∂ ∂ ∂ ∂
∂
∂
22
2
12 2 2
12
11
)} /
22
zz
f f signf Q signf
yf yf
∂∂
ΔΔ ⋅ + ⋅
∂∂ ∂∂
22
11
221222
11 2
{( )( )( ) ()}/
fy
zz
x
f signf f f signf f Q
xff f
∂∂
∂∂
ΔΔ + + ΔΔ + Δ
∂∂∂ ∂
В случае постоянных функций преобразования выражения
упрощаются, и можно записать в линейном приближении
()
()
2
112 2
(1)
1
2
12 2
12 2
1
1
f x f x f signf
Sx
y
f
f signf
f f signf
Δ+ Δ
Δ
Δ= +
−
−
, (3.1.23)
где
1
2
=signf для положительной обратной связи и 1
2
−=signf для
отрицательной обратной связи.
Соотношение для ошибки погрешности
y
δ
Δ
мало
информативно, поэтому не приводится.
В квадратичном приближении имеем
(1)
(1)
21 2
12 2
(2) (1)
1
12 2 12 2 12 2
11
121 21
f f y signf
f
f y signf
fx
yy
f
f signf f f signf f f signf
ΔΔ
ΔΔ
ΔΔ
Δ=Δ+ + +
−− −
(3.1.24)
Определим математическое ожидание и дисперсию
погрешности
y
Δ
из соотношения (3.1.24.)
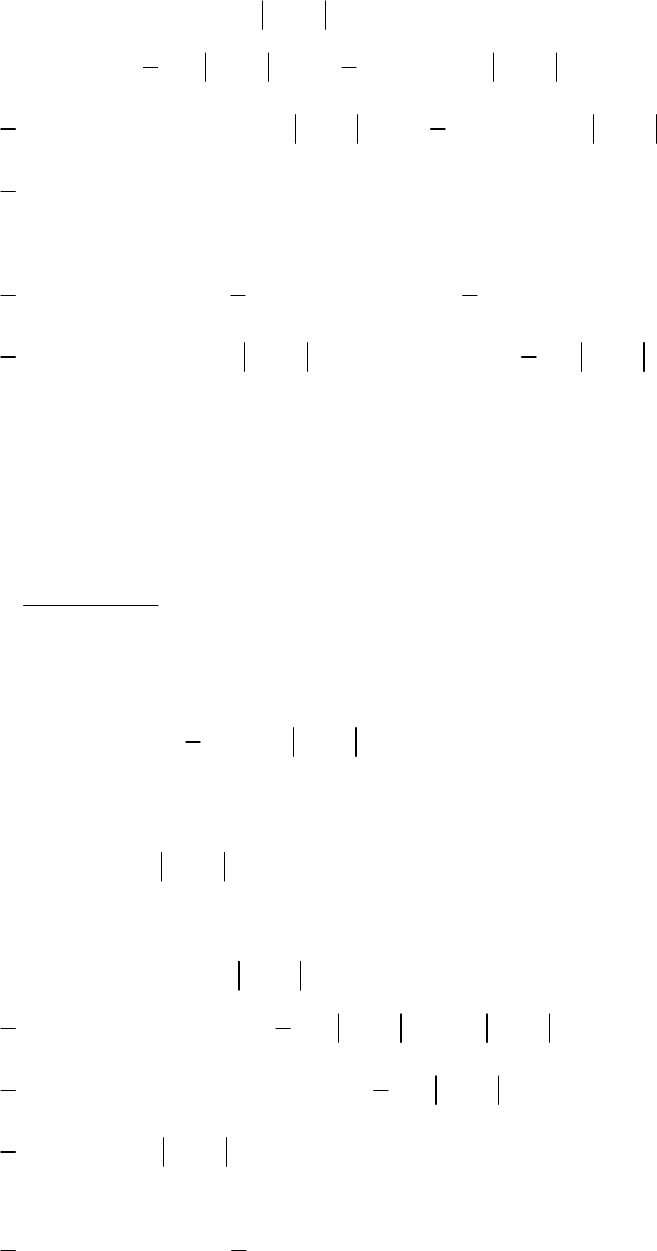
[
]
[
]
[
]
22 2
1122 1
/[]//
M
y xMfQ fxsignfMfQ SMxQΔ= Δ + Δ + Δ +
[] []
222
1122 212
11
(1 ) / /
22
M f x f f signf Q M f x f signf Q+ΔΔ⋅− + ΔΔ +
[]
()
2
33
121 2 12 2 1 2 2
11
(1 ) / /
22
M f f f xsignf f f signf Q M f f x signf Q
⎡⎤
+ΔΔ + + Δ +
⎣⎦
23 3
21
1
[( ) ] /
2
M
ffxQ+Δ , (3.1.25)
[
]
[
]
[
]
42
2424 2
1121
/[]/ /Dy xDf Q fxDf Q SDxQΔ= Δ + Δ + Δ +
() ()
[]
22
22 6 62 6 4 4
21 1 2 12
111
///
444
f
xD f Q f xD f Q f D f x Q
⎡⎤ ⎡⎤
+Δ+Δ+ΔΔ
⎣⎦ ⎣⎦
[] []
22 2 6 2 4
112122 1 122
11
(1 ) / (1 ) /
42
f
x D f f f f signf Q D f x f f signf Q+ΔΔ+ +ΔΔ− . (3.1.26)
В соотношениях (3.1.25, 3.1.26) введено обозначение Q=1-
f
1
f
2
signf
2
и учтено, что
()
2
2
1signf
=
.
Определим относительную погрешность. Для
рассматриваемой схемы связь между входом и выходом
представима в виде (см.§1.3.):
221
1
1 signfff
xf
y
−
=
. (3.1.27)
Из соотношений (3.1.24) и (3.1.27) после преобразований
получим:
(1) (1)
112212
1
()/
2
y
y x f y f f signf f f Q
δδ δδ δ δδ
=+ + + , (3.1.28)
где
(1)
y
δ
- относительная погрешность сигнала на выходе в линейном
приближении
(1)
112 22
()/y f f f signf f Q x
δ
δδδ
=+ +. (3.1.28а)
Для математического ожидания и дисперсии относительной
погрешности имеем соответственно:
11222
[] [ ]/ [ ]/ []
M
yMfQffsignfMfQMx
δδ δ δ
=+ ++
22 2
12 2 1 12 2 12 2 1 2
11
[( ) ] / (1 ) [ ]/
22
f f signf M f Q f f signf f f signf M f f Q
δδδ
+++ +
22 2 2
12 2 1 12 2
11
[( ) ]/ [ ](1 ) /
22
f
f M f Q M f x f f signf Q
δδδ
++++
212 2
1
[] /
2
M
f x f f signf Q
δδ
+ , (3.1.29)
222 2
1122
[] [ ]/ [ ]/ []Dy Df Q ffDf Q Dx
δδ δ δ
=+ ++
22 44
24 24
112 12 2
11
[( ) ] / [( ) ] /
44
Df ffQ ffDf Q
δδ
+++
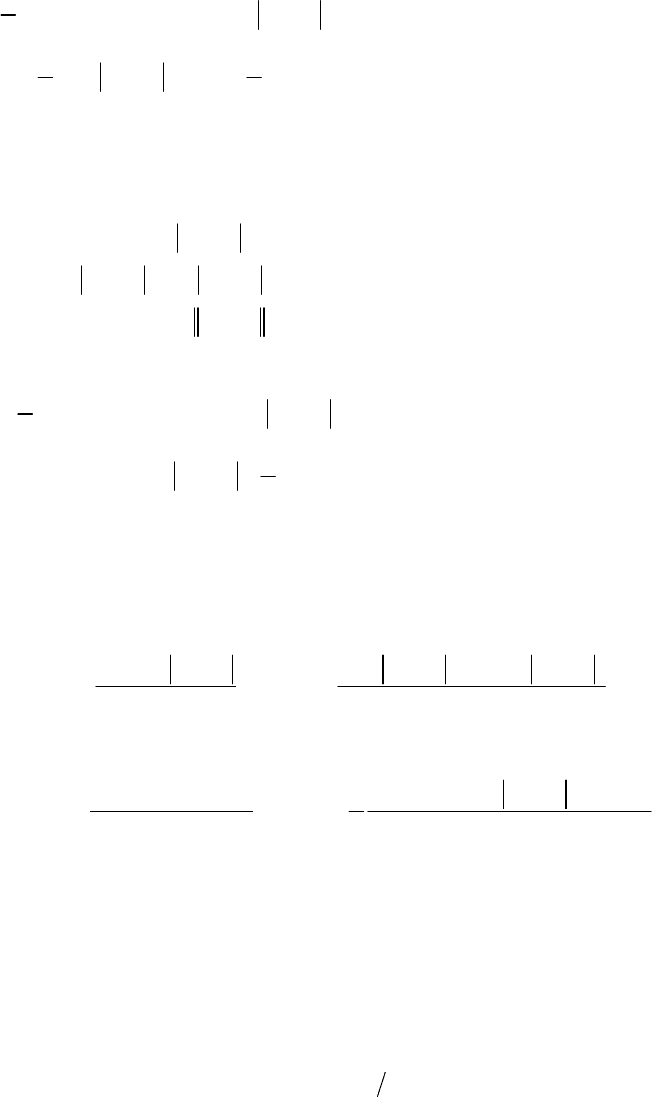
22 2 4
1212 12 2 1
1
[](1 )/[]
4
D f f f f f f signf Q D f x
δ
δδδ
++⋅
22 222
12 2 2 1 2
11
(1 ) / [ ] /
24
f
f signf Q D f x f f Q
δδ
++ . (3.1.30)
Если положить
(
)
iconstf
i
=
δ
, то выражения для
математического ожидания и дисперсии упрощаются:
[
]
()
[
]
[
]
12 2 1
1/
M
yffsignfMfQMx
δδδ
=+ + +
22
12 2 12 2 1
(1 ) [( ) ] /f f signf f f signf M f Q
δ
++
1122
[](1 )/
M
f x f f signf Q
δδ
++ , (3.1.29а)
[
]
22 2
12 1
[](1 )[ ]/Dy ffDf Q Dx
δδδ
=+ + +
222 33 44 4
11212 212
1
[( ) ]( ) /
2
D f ff ff signf ff Q
δ
++++
22 2
112212
1
[](1 )/
2
D f x f f signf f f Q
δδ
++ . (3.1.30а)
Если к тому же погрешность входного сигнала пренебрежимо
мала
(0)
x
δ
= , то выражения для математического ожидания и дис-
персии преобразуются к виду
[] []
()
()
12 2 12 2 12 2
1
2
12 2
12 2
2
1
1(1)
1
1
[]
f
f signf f f signf f f signf
My Mf
f f signf
f f signf
Mf
δδ
δ
++
=+ ⋅
−
−
⋅
(3.1.29б)
[]
()
[]
()
22 22
22
12 12 2 12
12
1
24
12 2
12 2
(1 )
11
2
1
1
f
f f f signf f f
ff
Dy Df
f f signf
f f signf
δδ
++
+
=+ ⋅
−
−
()
2
1
Df
δ
⎡⎤
⋅
⎣⎦
. (3.1.30б)
Из соотношений (3.1.29б, 3.1.30б) следует, что при f
1
=f
2
=1 и
signf
2
=−1(отрицательная обратная связь)
[
]
yM
δ
в линейном
приближении, вообще говоря, не равно нулю и зависит от
[
]
1
M
f
δ
;
этот вывод справедлив и в квадратичном приближении; для
дисперсии имеем
[]
[
]
2
1
fDyD
δ
δ
= , т.е. результат получается таким
же, как и в параллельной схеме с двумя элементами. При
положительной обратной связи, когда f
1
=f
2
=1 и signf
2
=1,
[]
yM
δ
и
[]
yD
δ
не определены, а именно,
[
]
∞
→yM
δ
и ∞→][ yD
δ
. Их
конечность можно обеспечить только при
0][
=
fM
δ
и
[]
0=fD
δ
.
Полученные соотношения для погрешности выходного сигнала
типовых схем позволяют провести анализ и расчет погрешности

измерения для СИ, имеющих сложную структуру, которая
представлена в виде комбинации типовых структур.
Рассмотрим в качестве примера измерительную систему на
нейронных сетях (см. §1.3).Каждый нейрон сети представляет
собой систему с многими входами и одним выходом (см.
рис.13г), и погрешность преобразования рассчитывается из
соотношений (3.1.22), (3.1.22а). Первый слой является
параллельным объединением m
нейронов, на вход каждого из
которых подается n сигналов. Второй слой (скрытый) состоит из
p нейронов, на вход каждого из которых подается m сигналов,
содержащих погрешности
(
)
1
j
yΔ , с выходов нейронов 1-го слоя. На
выходе каждого нейрона скрытого (2-го) слоя получается сигнал,
содержащий суперпозицию погрешностей
(
)
1
j
yΔ и
()
2
q
yΔ . На вход
каждого нейрона третьего слоя подается p сигналов,
содержащих погрешности
(
)
1
j
yΔ и
(
)
2
q
yΔ с выходов нейронов 1-го и
2-го слоев. На выходе каждого нейрона 3-го слоя получается
сигнал, содержащий суперпозицию погрешностей
()
1
j
yΔ ,
()
2
q
yΔ и
()
3
r
yΔ , где
()
1
j
yΔ - погрешность преобразования при прохождении
первого слоя, определяемая соотношениями (3.1.22) или
(3.1.22а);
mj ,1= ;
()
2
q
yΔ - погрешность преобразования при
прохождении второго (скрытого слоя), определяемая аналогично
первому слою;
pq ,1= ;
(
)
3
r
yΔ - погрешность преобразования при
прохождении сигналом 3-го слоя;
lr ,1= . В линейном
приближении, используя соотношение (3.1.22), имеем систему
уравнений
() ()() ()
∑
=
Δ=Δ
n
i
i
j
i
jj
xSy
1
11
- для первого слоя, (3.1.31а)
() ()() ()
22
1
m
uu
qqq
u
y
Sy
=
Δ= Δ
∑
- для второго слоя, (3.1.31б)
где
()
u
q
yΔ - погрешность сигнала на входе нейрона q 2-го слоя,
получившаяся на выходе нейрона
u 1-го слоя
() ()() ()
∑
=
Δ=Δ
p
rrr
ySy
1
33
υ
υυ
- для 3-го слоя, (3.1.31в)
где
()
υ
r
yΔ - погрешность сигнала на входе нейрона r 3-го слоя,
получившаяся на выходе нейрона
υ
2-го слоя.
Из приведенных уравнений видно, что погрешность
сигнала на выходе нейронной сети (погрешность
преобразования) зависит от погрешности сигнала на выходе
каждого нейрона 1-го и 2-го слоев.
Пример 1. Оценим погрешность функционирования
измерительной системы на нейронных сетях с учетом
погрешности входного сигнала и погрешности преобразования.
Используем результаты § 1.3. Обозначим, как и выше, j=1,…,m -
число нейронов в первом (входном) слое, q=1,…,p - число
нейронов во втором (
скрытом) слое, r=1,…,l - число нейронов в
третьем слое. Модель отдельного нейрона представляет собой
последовательное соединение сумматора n→1 (много входов –
один выход), персептрона и точки ветвления. Примем, что
сумматор вычисляет линейную функцию входов
1
1
()
n
ii
n
i
gx g x a x a
+
=
≡= +
∑
, (3.1.32)
где параметр a
n+1
соответствует аддитивной погрешности, а
некоторые параметры a
i
могут равняться нулю. Для персептрона
используем сигмоидальную функцию преобразования
1
() (1 exp( ))
f
xkx
−
=+ − . (3.1.33)
Для нейрона первого слоя сети погрешность на выходе
сумматора дается следующим соотношением
(1)( ) ( ) (1)( )
11
nn
ii i
jjj j
ii
zSx g
==
Δ= Δ + Δ
∑∑
, (3.1.34)
где
Δ
x
j
(i)
– погрешность сигнала i на входе нейрона j; S
j
(i)
–
чувствительность сумматора нейрона j по входному сигналу i;
вторая сумма определяет погрешность преобразования,
вызванную отклонением реальной функции преобразования
сумматора от номинальной. В общем случае она представима в
виде
00
() () (0) ( / ) ...gx g x g x g g x xΔ≡ − =Δ +∂Δ∂ +
. (3.1.35)
В линейном приближении учитываются только два первых члена,
т.е. аддитивная и мультипликативная составляющие. Для
Δ
z
j
имеем (индекс (1) опущен)
() () () () ()
01
11
()
nn
ii i ii
jjj j j
j
n
ii
zSx aaxa
+
==
−Δ= Δ + +
∑∑
. (3.1.36)
Сигнал z
j
+
Δ
z
j
поступает на вход персептрона, на выходе
которого получаем
1
()(1exp(()))
jjj jjj
yfz z kz z
−
=+Δ=+−+Δ
. (3.1.37)
Используя разложение в ряд с точностью до членов, линейных по
Δ
z
j
, получим для сигнала на выходе с учетом погрешности
сигнала на входе
(1 )
j
jj j j
yf
zkz=+Δ, (3.1.38)
где f
j
z
j
≡
f
j
(z
j
)
≡
f
j
. Если учесть также составляющую, обусловленную
погрешностью преобразования, то суммарная погрешность
сигнала на выходе нейрона j первого слоя дается выражением
(1) (1) (1) (1) (1) (1)
j
jj j jj
y
k
f
z
f
zΔ= Δ+Δ . (3.1.39)
Здесь
(1) (1) (1) (1) (1) (1) (1)
0
(1 )( )
jj j j j j
j
f
z
ff
kkzΔ=− − , (3.1.39а)
(1) (1)( ) (1)( ) (1)( )
1
1
n
ii j
jjj
n
i
zaxa
+
=
=+
∑
, (3.1.39б)
(1) (1)( ) (1)( ) (1)( ) (1)( ) (1)( ) (1)( )
01
11
()
nn
ii i ii j
jjj j j
jn
ii
zSx aaxa
+
==
Δ= Δ + − +
∑∑
. (3.1.39в)
Из выражения (3.1.39) следует, что погрешность сигнала на
выходе зависит от входного сигнала и его погрешности. Для
второго слоя имеем
(2) (2) (2) (2) (2) (2)
qqqq qq
ykfz fzΔ= Δ+Δ . (3.1.40)
Здесь
(2) (2) (2) (2) (2) (2) (2)
0
(1 )( )
qq q q q q
q
f
zf fkkzΔ=− − , (3.1.40а)
(2) (2)( ) (2)( ) (2)( )
1
1
m
uu q
qqq
m
u
zbyb
+
=
=+
∑
, (3.1.40б)
(2) (2)( ) (2)( ) (2)( ) (2)( ) (2)( ) (2)( )
01
11
()
mm
uu u uu q
qqq q q
qm
uu
zSy bbyb
+
==
Δ= Δ + − +
∑∑
, (3.1.40в)
где
Δ
y
q
(2)
– погрешность сигнала на выходе нейрона q второго
слоя;
Δ
y
q
(2)(u)
– погрешность сигнала на входе нейрона q второго
слоя, получившаяся на выходе нейрона u первого слоя; y
q
(2)(u)
–
сигнал на входе нейрона q второго слоя с выхода нейрона u
первого слоя
(2)( ) (1) (1)u
quu
yfz= , (3.1.40г)
где z
u
(1)
дается выражением (3.1.39б); а
Δ
y
q
(2)(u)
– выражением
(3.1.39), при этом следует положить j=u. Аналогично для
погрешности сигнала на выходе нейрона r третьего слоя
(погрешности результата измерения) можно записать
(3) (3) (3) (3) (3) (3)
rrrr rr
ykfz fzΔ= Δ+Δ . (3.1.41)
Здесь
(3) (3) (3) (3) (3) (3) (3)
0
(1 )( )
rr r r r r
r
f
zf fkkzΔ=− − , (3.1.41а)
(3) (3)( ) (3)( ) (3)( )
1
1
p
vv r
rrr
p
v
zcyc
+
=
=+
∑
, (3.1.41б)
(3) (3)( ) (3)( ) (3)( ) (3)( ) (3)( ) (3)( )
01
11
()
p
p
vv v vv r
rrr r r
rp
vv
zSy ccyc
+
==
Δ= Δ + − +
∑∑
, (3.1.41в)
где
Δ
y
r
(3)
– погрешность сигнала на выходе нейрона r третьего
слоя;
Δ
y
r
(3)(v)
– погрешность сигнала на входе нейрона r третьего
слоя, получившаяся на выходе нейрона v второго слоя; y
r
(3)(v)
–
сигнал на входе нейрона r третьего слоя с выхода нейрона v
второго слоя
(3)( ) (2) (2)v
rvv
yfz= , (3.1.41г)
где z
v
(2)
и
Δ
y
r
(3)(v)
даются выражениями (3.1.40б) и (3.1.40)
соответственно, при этом следует положить q= v.
Пример 2. Пусть входные сигналы x
i
, поступающие на вход
нейронной сети, являются нечеткими, т.е. представимы в виде
нечетких чисел или нечетких интервалов. Функции
преобразования сумматора и персептрона также будем считать
нечеткими, что позволяет учесть неопределенность
(погрешность) преобразования, используя соответствующий
способ задания сигналов и функций. В этом случае выходной
сигнал получается нечетким и содержит неопределенность,
обусловленную
нечеткостью входного сигнала и параметров
нейронной сети. Рассмотрим цепочку преобразований на входе
нейрона j первого слоя сети. Определим нечеткую функцию
~
()gx
из соотношения (3.1.32). Сначала вычислим нечеткие
произведения вида
~
ii
ax. Имеем для i=1
~~~
(1 ) (1 ) (1 )
11 1 1
111
(1 ) (1 ) (1 )
111
() supmin((),())
jjj
j
jj
ax a x
ouv
ouv
μ
μμ
=
=
. (3.1.42а)
Здесь и далее мы будем использовать операции sup и min для
объединения и пересечения, хотя возможны и другие пары
операций, например, sup• (• -произведение), inf sum и т.д.
Аналогично для произвольного i можно записать
~~~
(1 ) (1 ) (1 )
(1 ) (1 ) (1 )
() supmin((),())
jjj
ii i i
iii
j
jj
iii
ax a x
ouv
ouv
μ
μμ
=
=
, (3.1.42б)
Наконец, для i=n
~~~
(1 ) (1 ) (1 )
(1 ) (1 ) (1 )
() supmin((),())
nn n n
jjj
nnn
j
jj
nnn
ax a x
ouv
ouv
μ
μμ
=
= . (3.1.42в)
Теперь определим операцию суммирования
~~~
(1 )
(1 ) (1 ) (1 )
11 2 2
2
21 2
(1 ) (1 ) (1 )
212
() sup min( ( ), ( ))
j
jjj
j
jj
ax a x
g
too
too
μ
μμ
=+
=
, (3.1.43а)
~~~
(1 ) (1 )
(1 ) (1 ) (1 )
1
1
(1 ) (1 ) (1 )
1
() sup min( (), ( ))
jj
jj j
ii
i
i
ii
i
j
jj
ii
i
ax
gg
tto
tto
μ
μμ
−
−
−
=+
=
, (3.1.43б)
где i=2,…,n;
~~
1
11
gax= . На выходе сумматора получается нечеткий
сигнал, определяемый выражением
~~~
(1 ) (1 )
(1 ) (1 ) (1 )
1
1
11
(1 ) (1 ) (1 )
11
() sup min( (), ( ))
jj
jj j
n
n
n
n
nn
j
jj
n
nn
a
gg
ttu
ttu
μ
μμ
+
+
++
++
=+
=
. (3.1.44)
Этот сигнал поступает на вход персептрона с нечеткой
функцией преобразования вида (3.1.33). Имеем цепочку
соотношений
~~~
(1 ) (1 ) (1 )
(1 )
(1 ) (1 ) (1 )
11
11
(1 ) (1 ) (1 )
11
() supmin( (), ())
jjj
j
jjj
nn
n
j
jj
n
k
kg g
t
t
ρρ
μ
ρμρμ
++
+
+
=⋅
=
, (3.1.45)
~~
(1 ) (1 )
(1 ) (1 )
(1 ) (1 )
11
(1 ) (1 )
() supmin(1, ())
jj
jj
jj
nn
j
j
kg kg
ωρ
μ
ωμρ
++
−
=−
= , (3.1.46)
~~
(1 ) (1 )
(1 ) (1 )
(1 ) (1 )
11
1
(1 ) (1 )
1
exp( )
exp( )
() supmin(1, ())
jj
jj
jj
nn
j
j
kg kg
ωω
μ
ωμω
++
−−
=
=
, (3.1.46а)
~~
(1 ) (1 )
(1 ) (1 )
(1 ) (1 )
11
21
(1 ) (1 )
21
1 exp( ) exp( )
1
() supmin(1, ())
jj
jj
jj
nn
j
j
kg kg
ωω
μ
ωμω
++
+− −
=+
=
.
(3.1.46б)
Выходной сигнал нейрона j первого слоя сети дается
выражением
~~
(1 )
(1 )
(1 ) (1 )
1
1
2
(1 ) (1 )
2
1 exp( )
()
() supmin(1, ())
j
j
jj
j
n
j
j
y
kg
w
w
ω
μ
μω
−
+
+−
=
=
, (3.1.47)
где j=1,2….m; m-число нейронов в первом слое сети;
~
~~
(1 ) (1 )
1
1
(1 exp( ))
jj
j
n
ykg
−
+
=+ − ;
~
~~
(1 )
11
...
j
nnn
gax ax=++ ;
~~
~
(1 ) (1 )
11
jj
n
nn
gga
+
+
+= .
Отметим, что соотношения (3.1.42а –3.1.47) могут быть
записаны в альтернативной форме через
α
-срезы
соответствующих нечетких множеств. Сигналы вида (3.1.47) с
выходов нейронов первого слоя подаются на вход каждого
нейрона второго слоя сети. Имеем цепочку преобразований,
аналогичную таковой для первого слоя с заменой индексов и
обозначений: (1j)→(2q); n→m;
~
~
ij
ab→ ;
~~
ij
x
y→ ;
~
(1 ) ( 2 )
~
j
q
kk→
.
На выходе нейрона q второго слоя сети получаем сигнал,
определяемый соотношением
~~
(2 )
(2 )
(2 ) (2 )
1
1
2
(2 ) (2 )
2
1 exp( )
()
() supmin(1, ())
q
q
q
qq
m
qq
z
kg
w
w
ω
μ
μω
−
+
+−
=
=
, (3.1.48)
где q =1,…,p;
~
~~
(2 ) (2 )
1
1
(1 exp( ))
qq
q
m
zkg
−
+
=+ − ;
~
~~
(2 )
11
...
q
mmm
gby by=++ ;
