Романов В.Н. Теория измерений. Основы теории точности средств измерений

Если частота

υ

ω

опорного напряжения синхронизирована с

частотой сигнала

(

)

υ

ω

=

, то выходное напряжение, которое

соответствует входному сигналу U

x

, имеет вид:

(

)

(

)

()

00

2sinsin

4cos cos2

ax

UUU t t

UU t

υ

υυ

υ

ωωϕ

ϕωϕ

⎡⎤

⎣⎦

=+=

=−+

. (2.4.4)

Этот сигнал проходит через фильтр (RC-цепочка c

12

g

RC

ω

= 

). На выходе фильтра получается арифметическое

среднее:

()

00

/4 cos

ax

UUU

υ

ϕ

=

. (2.4.5)

Такой выходной сигнал прямо пропорционален входному

сигналу и зависит от сдвига фаз

υ

ϕ

между входным и опорным

сигналами. Наилучшие результаты получаются при

υ

ϕ

=0°.

После смесителя вклад шума равен:

(

)

(

)

0

sin

aR R

UUtU t

υ

υυ

ω

ϕ

=+

. (2.4.6)

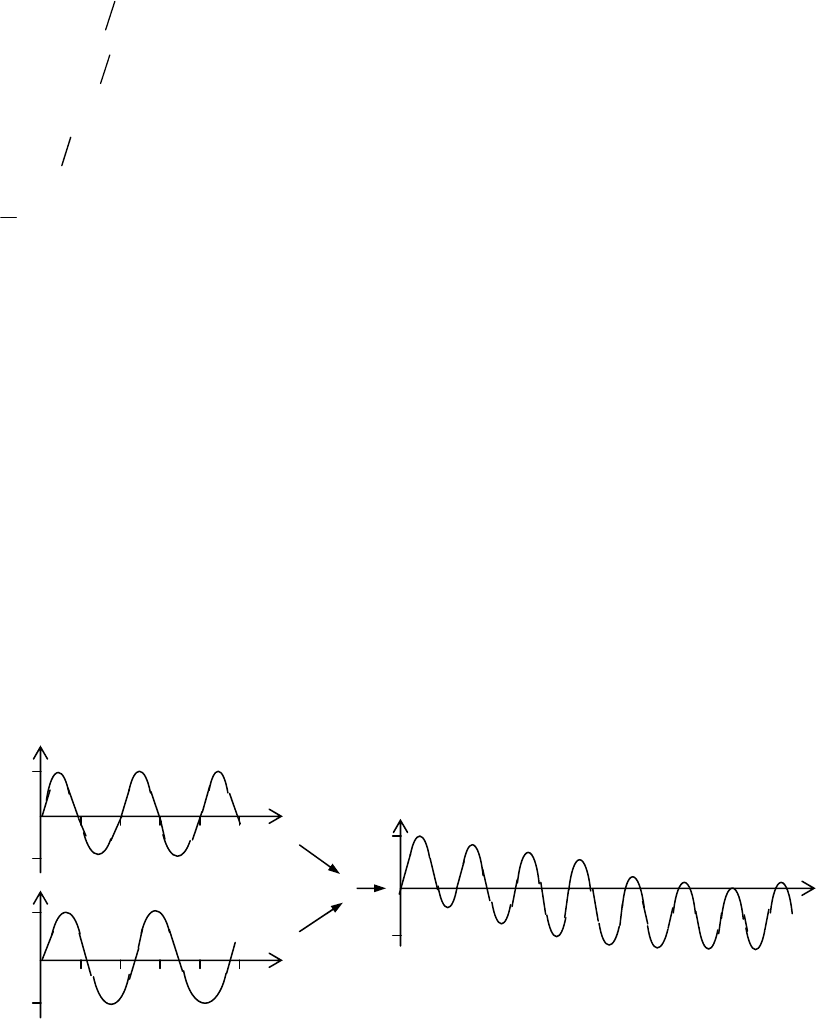
На рис.12 показан выходной сигнал для одной из тринадцати

гармоник шума с частотой ω

R

=(5/6)ω

υ

. Хорошо видно, что при

сложении с опорным сигналом возникают положительные и

отрицательные отклонения, которые компенсируются при

усреднении.

U

v

ω

v

U

R

⊗U

v

t

U

R

⊗ t

ω

R

=5/6ω

v

t

Рис. 12. Наложение двух периодических сигналов

с близкими частотами.

Если проводить усреднение достаточно долго, то

результирующий вклад шума будет очень мал. Для одной

гармонической составляющей шума можно преобразовать

выражение (2.4.6) с помощью тригонометрических формул

(предполагая, что φ

υ

=0):

(

)

00

sin sin

aR R R R

UUUtt

υ

ω

ωω

=

, (2.4.7)

()()

(

)

(

)

00

2cos cos

aR R R R R

UUU t t

υυυ

ωωωωω

=−−+

⎡⎤

⎣⎦

. (2.4.8)

Фильтр с верхней граничной частотой

g

υ

ω



дает на выходе

соответствующее усредненное значение

() () ()

aR R aR R

UHU

ω

ωω

=

. (2.4.9)

Используя выражение для RС-цепочки, получим:

()

22

00

2

cos

21 /

g

R

aR R R

R

UU

Ut

υ

ωωω

ωω ω

=−

⎡⎤

+−

⎣⎦

. (2.4.10)

Таким образом, из широкого спектра шумов

(

)

UR

W

ω

остается

узкая область возле частоты

υ

ω

, которая и определяет

остаточный шум. Эффективную ширину

эфф

ω

Δ

тоже можно

определить из (2.4.10):

эфф

22/

g

RC

ωω

Δ==

, (2.4.11)

эфф

1/ RC

νπ

Δ=

. (2.4.12)

Ее можно сделать как угодно малой, если увеличивать

постоянную времени RC. При этом, конечно, она не должна быть

больше характерного времени изменения измеряемой величины.

Такое интегрирование не влияет на сам сигнал, даваемый

выражением (2.4.5). Роль модулирующей частоты

υ

ω

состоит в

том, что измерения смещаются из частотной области сильных

шумов (например, 1/f-шума при низких частотах) в область, где

уровень шума мал.

Вопросы, изложенные в этой главе, рассмотрены в [12, 23,

25, 33, 36, 37, 38].

3. Методы оценки точности средств измерений

3.1 Метрологический анализ

Под метрологическим анализом понимается анализ

точности измерений или, в более узкой постановке, точности

функционирования СИ. Для его проведения необходимо

построить модель СИ, в частности, его структурной схемы.

Многообразие структурных схем СИ может быть сведено к

конечному набору типовых моделей, характеризуемых двумя

факторами: типом схемы и числом входов-выходов. Выделим

следующие типовые модели:

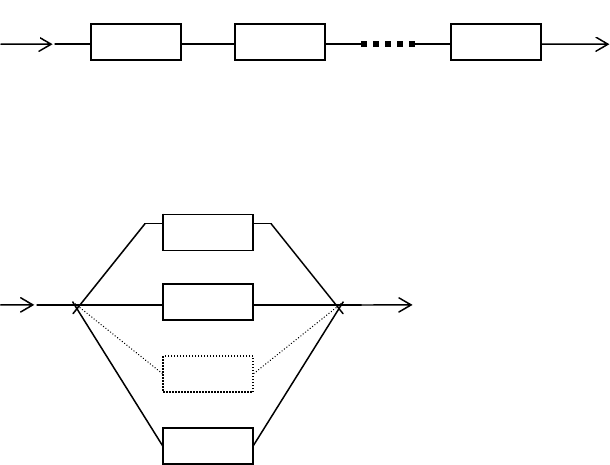
1) линейная с одним входом и одним выходом:

а) последовательное соединение элементов (рис.13а);

б) параллельное соединение элементов (рис.13б);

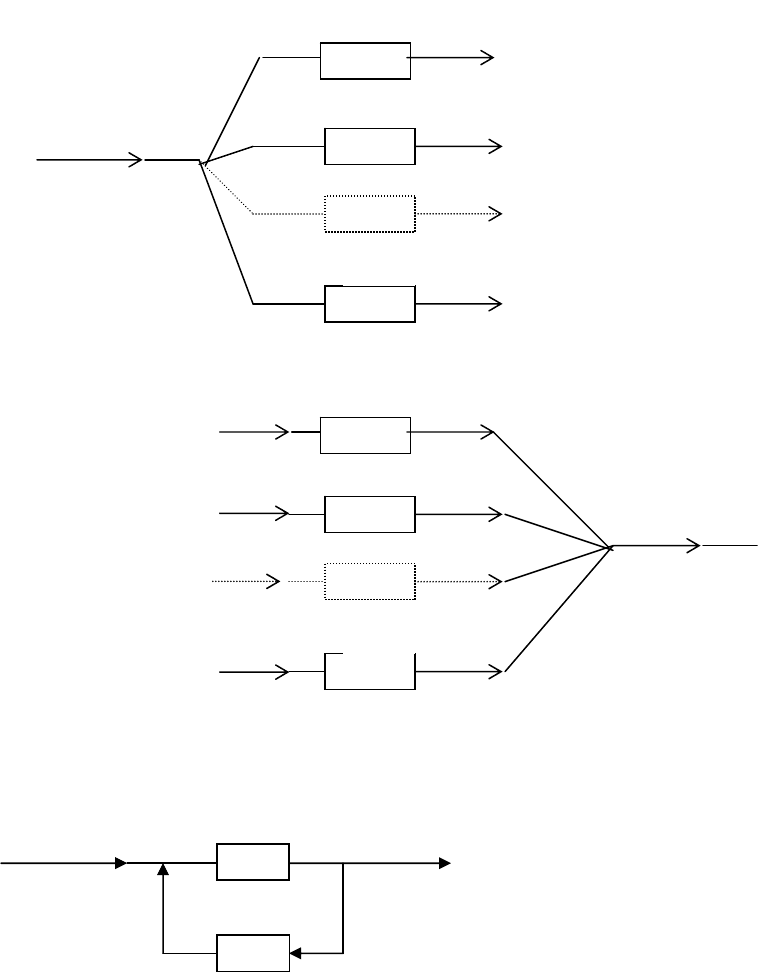
2) линейная с одним входом и многими выходами (рис.13в);

3) линейная с многими входами и одним выходом (рис.13г);

4) циклическая с одним входом и одним выходом (рис13д);

f

1

f

2

f

k

Рис.13а. Линейная схема с последовательным соединением элементов: х – входной сигнал,

y – выходной сигнал; f

1

,…,f

k

– функции преобразования отдельных элементов (СИ).

f

1

х

Рис.13б. Линейная схема с параллельным соединением элементов.

x

y

f

k

f

2

y

Ошибка!

Рис. 13в. Линейная схема с одним входом и многими выходами.

Рис.13г. Линейная схема с многими входами и одним выходом.

Рис.13д. Циклическая схема с одним входом и одним выходом.

Для схемы на рис. 13,а при произвольных функциях

преобразования погрешность в квадратичном приближении

определяется системой рекуррентных соотношений

x

f

(1)

f

(2)

f

(k)

y

1

y

2

y

k

y

f

(2)

f

(k)

x

2

x

k

f

(1)

x

l

x

f

2

f

1

y

22

11

22

11

() ( )

22

ii i i

ii i i i

ii i i

yy y y

yf y f y

fy f y

−−

∂∂ ∂ ∂

Δ= Δ+ Δ + Δ + Δ +

∂∂ ∂ ∂

2

1

(),1,...,

i

ii

y

f

yi k

fy

−

∂

+ΔΔ=

∂∂

. (3.1.1)

Вводя чувствительности S

i

=∂y

i

/∂y

i-1

, выражение (3.1.1) можно

записать в виде

2

22

11

2

1

11

() ( )

22

iii

iiii i i

iii

yyS

yfSy f y

ffy

−−

−

∂∂∂

Δ= Δ+Δ + Δ + Δ +

∂∂∂

1

()

i

ii

i

S

f

y

f

−

∂

+ΔΔ

∂

, (3.1.1а)

где y

i

=f

i

(y

i-1

); y=f

k

(f

k-1…

f

1

(x)); y

0

=x.

В частности, при i=1 (схема из одного элемента) имеем

22

11 1 1

11 1

22

11

() ()

22

yy y y

yfx f x

fx f x

∂∂ ∂ ∂

Δ= Δ+ Δ+ Δ + Δ +

∂∂ ∂ ∂

2

1

()

y

f

x

fx

∂

+ΔΔ

∂∂

, (3.1.1б)

где y

1

=y=f

1

(x);

Вводя чувствительность S

1

=∂y

1

/∂x, получим из (3.1.1б)

2

22

111

111 1

2

11

() ()

22

yyS

yy fSx f x

ffx

∂∂∂

Δ≡Δ= Δ+Δ+ Δ + Δ +

∂∂∂

1

()

S

f

x

f

∂

+ΔΔ

∂

. (3.1.1в)

В выражениях (3.1.1, 3.1.1в) два первых слагаемых

соответствуют линейному приближению. Для проведения

расчетов нужно знать вид функций преобразования. Рассмотрим

случай, наиболее важный для практики и, одновременно,

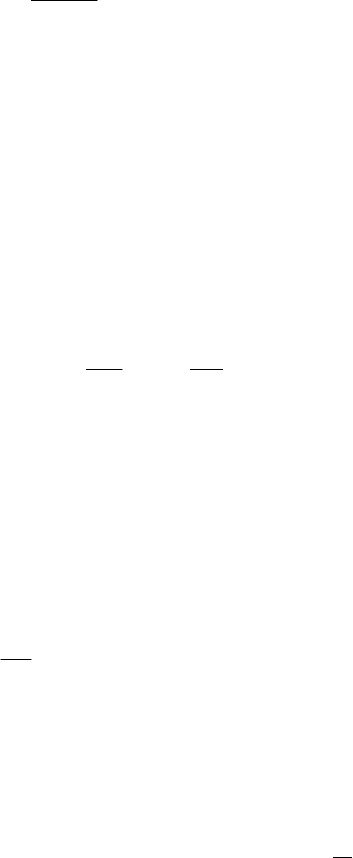
наглядный, когда функции преобразования элементов f

i

являются

постоянными. При учете только погрешности входного сигнала

имеем

1

i

ik

yS

х

Sx

=

Δ= Δ=Δ

∏

, (3.1.2)

где ∆y – погрешность сигнала на выходе; ∆х – погрешность

сигнала на входе, S – чувствительность схемы.

Относительная ошибка определения погрешности

выходного сигнала из (3.1.2) определяется выражением

1

()

k

yix

i

y

S

y

δ

δδ

ΔΔ

=

ΔΔ

≡=+

Δ

∑

, (3.1.3)

где

i

S

δ

– относительная ошибка определения чувствительности

i-го элемента схемы,

xΔ

δ

– относительная ошибка входного

сигнала. Отметим, что погрешность считается значимой, если

5.0<

Δy

δ

.

Выражение (3.1.2) не учитывает отклонение реальной

функции преобразования от идеальной (номинальной). При учете

этого фактора погрешность выходной величины находится из

соотношения:

1

k

i

yy

yfx

f

x

=

∂∂

Δ= Δ+ Δ

∂∂

∑

, (3.1.4)

где

i

fΔ – отклонение реальной функции от идеальной для i-го

элемента схемы.

Второе слагаемое в (3.1.4) определяется погрешностью

входного сигнала и совпадает с (3.1.2). Первое слагаемое

учитывает вклад элементов схемы из-за отличия реальной

функции преобразования от идеальной и записывается в виде

хfff

f

y

ij

kj

j

k

i

ii

k

i

∏

∑∑

≠

=

==

Δ=Δ

∂

1

11

, (3.1.4а)

Если учитывать не только линейные, но и квадратичные

члены по ∆х, то выражение для погрешности входной величины

принимает вид

11

(2) (1)

111

,

1

2

kkk

ij i jl

iij

jk lk

ji

ji lij

yy ff

х

fffх

===

==

≠

≠≠

Δ=Δ+Δ + Δ Δ +

∑∑∑

∏∏

+

1

k

ij

i

jk

ji

f

xf

=

≠

ΔΔ

∑

∏

, (3.1.5)

где

i

f

Δ – абсолютная погрешность функции преобразования, ∆y

(1)

определяется соотношением (3.1.2) и учтено, что в данном

случае S

i

= f

i

.

Определим математическое ожидание и дисперсию

погрешности. В линейном приближении при учете только

погрешности входного сигнала для математического ожидания и

дисперсии имеем соответственно из (3.1.2)

[] []

xMSyM

k

i

Δ=Δ

∏

=1

, (3.1.6)

[] []

xDSyD

k

i

Δ=Δ

∏

=1

2

, (3.1.7)

В более общем случае из соотношения (3.1.4) найдем

[] [] []

11

1

k

ij i

i

jk ik

ji

M

yMffxSMx

=

==

≠

Δ= Δ + Δ

∑

∏∏

, (3.1.6а)

[] [] []

2

11

1

k

ij i

i

jk ik

ji

Dy Df fx S Dx

=

==

≠

⎛⎞

⎜⎟

Δ= Δ + Δ

⎜⎟

⎝⎠

⎜⎟

⎝⎠

∑

∏∏

, (3.1.7а)

В квадратичном приближении из (3.1.5) найдем

[] [] []

11 1

111

,

1

[]

2

kkk

ij i ijl

iij

jk ik lk

ji

ji lij

My Mf fx SMx Mff f

х

===

== =

≠

≠≠

Δ= Δ + Δ+ ΔΔ +

∑∑∑

∏∏ ∏

1

[]

k

ij

i

jk

ji

M

fx f

=

≠

ΔΔ

∑

∏

, (3.1.6б)

[] [] []

2 2

2

11 1

111

,

1

[]

4

kkk

ij i ijl

iij

jk ik lk

ji

ji lij

Dy Df fx S Dx Dff fх

===

== =

≠

≠ ≠

⎛⎞ ⎛⎞

⎛⎞

⎜⎟ ⎜⎟

Δ= Δ + Δ+ ΔΔ +

⎜⎟

⎜⎟ ⎜⎟

⎝⎠

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

∑∑∑

∏∏ ∏

2

1

[]

k

ij

i

jk

ji

Dfx f

=

≠

⎛⎞

⎜⎟

ΔΔ

⎜⎟

⎝⎠

∑

∏

(3.1.7б)

Если погрешности

i

f

Δ

, ∆х – случайные центрированные, то

[]

0=Δ

i

fM и

[]

0=ΔxM

, т.е. и

[

]

0

=

Δ

yM

. Если

i

f

Δ

и ∆х –

систематические, то их математические ожидания отличны от

нуля, и, следовательно,

[

]

0

≠

Δ

yM . Аналогично рассчитываются

математическое ожидание и дисперсия погрешности в более

сложных случаях, однако результаты получаются менее

наглядными. Для многих СИ наряду с абсолютной погрешностью

целесообразно задавать относительную погрешность

y

δ

Δ

=

. Для

рассматриваемой схемы связь между входом и выходом

представима в виде (см.§ 1.3)

xfffy

kk 11

.....⋅⋅=

−

. (3.1.8)

Отсюда, используя соотношение (3.1.4), после преобразований

получим в линейном приближении

1

k

i

yfx

δ

δδ

=

=+

∑

, (3.1.9)

где

i

f

δ

- относительная погрешность функции преобразования i-

го элемента схемы; х

δ

- относительная погрешность входного

сигнала.

В квадратичном приближении после ряда преобразований

имеем

(2) (1)

11 1

1

2

kk k

ij i

ji

yy ff f

х

δ

δδδδδ

== =

≠

=+ +

∑∑ ∑

, (3.1.10)

где

(1)

y

δ

определяется выражением (3.1.9).

Если функции преобразования являются номинальными, то

0=

i

f

δ

и относительная погрешность выходного сигнала

определяется погрешностью входного сигнала.

Определим математическое ожидание и дисперсию

относительной погрешности. Считая погрешности

i

f

δ

некоррелированными, из (3.1.10) получим

[] []

M

yMx

δ

=+

[]

111

1

2

kkk

iij

ji

Mf M ff

δδδ

===

≠

⎡

⎤

+

⎣

⎦

∑∑∑

[]

1

k

i

M

fx

δ

=

∑

, (3.1.11)

[

]

[

]

Dy Dx

δδ

=+

[] []

1

111

1

4

kkk

iiji

iij ik

ji

Df Dff Dfx

δ

δδ δδ

=== =

≠

⎡⎤

++

⎣⎦

∑∑∑ ∑

(3.1.12)

При практических расчетах можно принять, что

погрешности

i

f

δ

и x

δ

независимы, поэтому

[

][][]

xMfMxfM

ii

δ

= ;

[

]

[

]

[

]

[

]

22

()

ii i

Dfx DfM x DxM f

δ

δδδ δδ

⎡⎤

=+

⎣⎦

. Аналогичное утверждение

справедливо также для

i

f

δ

и

j

f

δ

.

Если положить )(iconstf

i

=

δ

, т.е. погрешности для всех

элементов схемы одинаковы, и погрешность

x

δ

пренебрежимо

мала, то из (3.1.11) получаем

[] [ ]

()()

[]

2

1

2

1

ii

fMkkfkMyM

δδδ

−+=

(3.1.11а)

Соотношение (3.1.12) для дисперсии при тех же

предположениях принимает вид

[]

()()

[]

2

1

4

1

][

ii

fDkkfkDyD

δδδ

−+= (3.1.12а)

Таким образом, математическое ожидание и дисперсия

относительной погрешности выходного сигнала возрастает в k

раз по сравнению с соответствующими величинами для

отдельного элемента схемы (без учета квадратичных слагаемых).

Для схемы на рис.13,б в квадратичном приближении получается

следующее общее соотношение

22 2

(2) (1) 2 2

22

11 1

1

() 2 ( ) ( )

2

kk k

ii i

ii

ii i

ii

yy y

yy x xf f

xxff

== =

⎡⎤

∂∂ ∂

Δ=Δ+ Δ+ ΔΔ+ Δ

⎢⎥

∂∂∂∂

⎣⎦

∑∑ ∑

,

где Δy

(1)

– выражение для погрешности в линейном приближении;

y

i

=f

i

(x); y=y

1

+…+ y

k

. Для Δy

(1)

имеем

(1)

11

kk

i

ii

i

y

ySx f

f

==

∂

Δ= Δ+ Δ

∂

∑∑

,

Рассмотрим случай, когда функции преобразования

являются постоянными. В тех же обозначениях при учете только

погрешности входного сигнала имеем

1

k

i

ySx

=

Δ= Δ

∑

, (3.1.13)

причем

S

i

= f

i

.

Для относительной ошибки погрешности найдем

yx

S

δ

δδ

ΔΔ

=+, (3.1.14)

где

∑

=

k

i

SS

1

- чувствительность схемы.

Если учесть отклонение реальной функции преобразования

от идеальной, то выражение для абсолютной погрешности

принимает вид

(1)

11

kk

ii

yfxSx

==

Δ=Δ+ Δ

∑∑

, (3.1.13а)

В квадратичном приближении для погрешности получим

(2) (1)

1

k

i

y

yfx

=

Δ=Δ+ΔΔ

∑

, (3.1.13б)

Определим математическое ожидание и дисперсию

абсолютной погрешности из (3.1.13б)

[] [] [] [ ]

111

kkk

ii i

iii

M

yMfxSMxMfx

===

Δ= Δ + Δ+ ΔΔ

∑∑∑

, (3.1.15)

[] [] [] [ ]

2

11 1

kk k

ii i

Dy Dfx S Dx Dfx

== =

⎛⎞

Δ= Δ + Δ+ ΔΔ

⎜⎟

⎝⎠

∑∑∑

. (3.1.16)

Определим относительную погрешность. Для параллельной

схемы связь между входом и выходом представима в виде

(см.§1.3.)

∑

=

k

i

xfy

1

, (3.1.17)

С учетом (3.1.13а) после ряда преобразований получим

(1)

11

/

kk

ii i

ii

y

ff f x

δ

δδ

==

=+

∑∑

, (3.1.18)

В квадратичном приближении вместо (3.1.18) имеем

(2) (1)

11

/

kk

ii i

ii

y

yffxf

δδ δδ

==

=+

∑∑

, (3.1.18а)

где

)1(

y

δ

- определяется выражением (3.1.18).

Для математического ожидания и дисперсии относительной

погрешности имеем соответственно

[] [ ]

11

/[]

kk

ii i

ii

M

yfMffMx

δδ δ

==

=++

∑∑

[]

11

/

kk

ii i

ii

f

Mfx f

δδ

==

+

∑∑

, (3.1.19)

[] [ ] []

2

11

/

kk

ii i

ii

Dy f

D

ff

Dx

δδ δ

==

⎛⎞

=++

⎜⎟

⎝⎠

∑∑

[]

2

11

/

kk

ii i

ii

f

Dfx f

δδ

==

⎛⎞

+

⎜⎟

⎝⎠

∑∑

(3.1.20)

Если принять, что

(

)

i

f

const i

δ

=

, то (3.1.19), (3.1.20)

упрощаются

[] [ ] []

[

]

ii

M

yMf MxMfx

δ

δδδδ

=++ , (3.1.19а)

[] [ ] []

2

11

/

kk

ii i

ii

Dy

D

ff f

Dx

δδ δ

==

⎛⎞

=++

⎜⎟

⎝⎠

∑∑

Романов В.Н. Теория измерений. Основы теории точности средств измерений

Подождите немного. Документ загружается.