Roff D.A. Modeling Evolution: An Introduction to Numerical Methods
Подождите немного. Документ загружается.

Note that this function does not consist of a single equation but a series of steps that
evaluate whether survival after being calculated according to As–Bs*xshouldbe
reset to 0 or 1. The function adapt calls INTEGRAND and adapt is called by the
function FITNESS, which is itself called by nlm or optimize in the main program.
R CODE:
rm(list¼ls()) # Remove all objects from memory
library(adapt) # Make sure that adapt is loaded
INTEGRAND <- function(Y,x) # Define function to be integrated
{
Af <-2;Bf<- 2 # Invariant parameter values
Ca <- 1/0.7; Cb <-5
# Y[1] ¼ As and Y[2] ¼ Bs
Surv <- Y[1]-Y[2]*x # Vector of survivals
# Check that no survival < 0. If so then set to zero
Surv[Surv<0] <-0
# Check that no survival > 1. If so then set to 1
Surv[Surv>1] <-1
return((AfþBf*x)*Surv*Cb*Ca )
}
FITNESS<- function(x) # Function that calls adapt for a given x
{
Amin <- 0.3; Amax <- 1 # Min and max values of a
S
Bmin <- 0; Bmax <- 0.2 # Min and max values of b
S
W <- adapt(2, lo¼c(Amin,Bmin), up¼c(Amax,Bmax), minpts ¼ 1000,
functn¼INTEGRAND, x¼x)
return(-W$value) # Return negative of fitness
}
# MAIN PROGRAM
nlm(FITNESS,p ¼1,steptol¼1e-5) # Note change in steptol
optimize(f¼FITNESS,interval¼c(1,4), maximum¼FALSE)#Alternate
method
OUTPUT: (modified slightly)
> nlm(FITNESS,p=1,steptol = 1e-5)
$minimum
[1] −2.897318
$estimate [1] 3.324141
$gradient [1] −0.01254321
$code [1] 2
$iterations [1] 13
> optimize(f=FITNESS,interval=c(1,4), maximum=FALSE)
$minimum [1] 3.368978
$objective [1] −2.897131
The two routines nlm and optimize give
slightly different answers. The termina-
tion code for nlm indicates that it is not clear that a minimum has been attained.
98 MODELING EVOLUTION
In fact it was necessary to change the default step tolerance steptol from 1e-6
to 1e-5 to achieve this (further changes did not change the result). Notice also that
minpts in adapt has been changed from its default of 100 to 1,000. These
changes were made to try and make the two optimization routines agree as
much as possible. It is very important to carefully check the results of numerical
methods by several pathways, if at all possible.
MATLAB CODE: See Section 2.18.14.
2.8.5 Finding the maximum using a numerical approach
The approach used here is a mixture of a brute force approach and non-linear
optimization. For each value of x 10,000 values are calculated and nlm then used to
locate the value of x at which fitness is maximized (i.e., –W is minimized). To check
on consistency the process is replicated 10 times and the mean and standard
deviation calculated. Note that the random number seed is given outside the
replication loop (or we would just be generating the same sequence each time)
and that the same set of random parameter values are used within a replicate run.
R CODE:
rm(list¼ls()) # Remove all objects from memory
FITNESS <- function(x,As,Bs)
{
Af <-2;Bf<- 2 # Invariant parameter values
Surv <-AsBs*x # Vector of survivals
# Check that no survival < 0. If so then set to zero
Surv[Surv<0] <-0
# Check that no survival > 1. If so then set to 1
Surv[Surv>1] <-1
W <- mean((AfþBf*x)*Surv)
return(-W)
}
# MAIN PROGRAM
Amin <- 0.3; Amax <- 1 # Min and max values of aS
Bmin <- 0; Bmax <- 0.2 # Min and max values of bS
# Calculate n parameter combinations
n <- 10000 # Number of values of a
S
and b
S
to generate
# We are assuming a uniform distribution of values
# Make several runs. Here we use 10
REP <- matrix(0,10) # Create matrix to hold replicate
set.seed(10) # Set seed for random number generator
for(i in 1:10) # Iterate over replicates
{
Bs <- runif(n, min¼Bmin, max¼Bmax) # Vector of values of Bf
As <- runif(n, min¼Amin, max¼Amax) # Vector of values of As
REP[i]<- nlm(FITNESS,p¼REP[i],As,Bs)$estimate # Optimum for
this run
FISHERIAN OPTIMALITY MODELS 99
}
print(c(mean(REP), sd(REP))) # Print mean and standard deviation
OUTPUT:
[1] 3.36934528 0.03739426
The mean of the 10 replicate runs closely matches that obtained using optimize
(3.368978). Because of the time required to do the numerical integration, there
was little difference in run time between the two approaches.
MATLAB CODE:See Section 2.18.15.
2.9 Scenario 7: Discrete temporal variation in parameters
In the real world values will vary among generations either because of genetic or
environmental variation. In this scenario we shall consider the consequences of
discrete temporal stochastic variation in a single parameter. Within each genera-
tion the parameter takes a particular value for all individuals. As in Scenario 6, the
particular case is conceptually the same as in Scenario 1, except that a parameter
of the survival function varies temporally.
2.9.1 General assumptions
1. The organism is semelparous.
2. Fecundity, F, increases with body size, x.
3. Survival, S, decreases with body size, x.
4. At least one of the parameters in the functions describing the above two traits is
temporally variable.
5. Fitness, W, is a function of fecundity and survival.
2.9.2 Mathematical assumptions
1. Fecundity increases linearly with body size:
F ¼ a
F
þ b
F
x ð2:46Þ
where a
F
and b
F
are constants.
2. Survival decreases linearly with body size:
S ¼ a
S
b
S;i
x ð2:47Þ
where b
S,i
varies from generation to generation, as indexed by i. In this particular
case b
S
takes one of the following values with the probability, P
i
, shown in
parentheses: 0.10 (0.1), 0.12 (0.3), 0.14 (0.4), or 0.2 (0.2). Note that the sum of the
probabilities must be 1.
3. In a deterministic world fitness, W, is the expected lifetime reproductive
success, R
0
, given as the product of Fecundity and Survival. However, in a
100 MODELING EVOLUTION
temporally variable environment the appropriate measure of fitness is the
geometric average (Roff, 2002, chapter 1):
W ¼
Y
i¼4
i¼1
½ða
F
þ b
F
xÞða
S
b
S;i
xÞ
P
i
ð2:48Þ
Working with products is generally not a good policy as the numbers can quickly
become very small or large. It is more convenient to take logs, thus converting the
product into a summation:
log W ¼ log
Y
i¼4
i¼1
½ða
F
þ b
F
xÞða
S
b
S;i
xÞ
P
1
¼
X
i¼4
i¼1
P
i
log½ða
F
þ b
F
xÞða
S
b
S;i
xÞ
ð2:49Þ
As always, we first ask if fitness has a maximum value at an intermediate value
of x.
2.9.3 Plotting the fitness function
Because we have converted the fitness function to a summation there is nothing
new introduced here. Parameter values are given in the function. An important
aspect is that W approaches minus infinity as x approaches 3 and so the range in
x is kept below 3.
R CODE:
rm(list¼ls()) # Remove all objects from memory
FITNESS <- function(x) # Function to calculate log of fitness
{
Af <-2;Bf<-2;As<- 0.6 # Parameter values
pBs <- c(0.1,0.3,0.4,0.2) # Vector of probabilities for Bs
Bs <- c(0.1,0.12,0.14,0.2) # Vector of Bs values
W.ind <- (AfþBf*x)*(AsBs*x) # Fitness values for each Bs value
log.W <- -sum(pBs*log(W.ind)) # log Fitness
return(log.W)
}
# MAIN PROGRAM
x <- matrix(seq(0,2.99,length¼100))# Values. Note W ¼INF at x¼3
LOG.W <- apply(x,1,FITNESS) # Calc log(fitness) values
# Plot fitness¼exp(-W) vs x
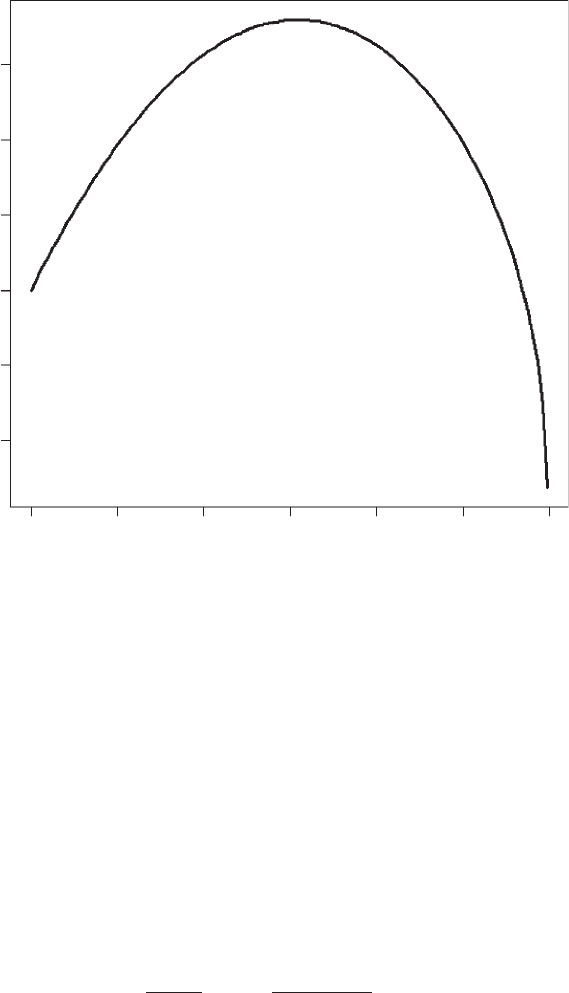
plot(x,exp(-LOG.W),xlab¼“Body size, x”,ylab¼“Fitness, W”,
type¼’l’,las¼1, lwd¼3)
Fitness is maximized in the vicinity of 1.5 (Figure 2.7) and body size can never
equal or exceed 3.0, as fitness becomes negative.
MATLAB CODE: See Section 2.18.16.
FISHERIAN OPTIMALITY MODELS 101
2.9.4 Finding the maximum using the calculus
To discuss the general approach to the analysis of the type of equation shown in
(2.49) we shall write it in a more general form as
logW ¼
X
P
i
log½f ðy
i
; xÞ ð2:50Þ
where f(y
i
, x) means “a function of x (the trait of interest) and y
i
the variable
parameter (in the present case ¼ b
S,i
).” In this form the equation presents no
difficulty as it can readily be differentiated with respect to x for all individual
values of y
i
:
dlogW
dx
¼
X
P
i
dlog½f ðy
i
; xÞ
dx
ð2:51Þ
which in the present scenario gives
0.0
0.8
1.0
1.2
1.4
1.6
1.8
Body size, x
0.5 1.0 1.5 2.0 2.5 3.0
Fitness, W
Figure 2.7 Scenario 7: Fitness versus body size.
102 MODELING EVOLUTION

logW ¼
X
i¼4
i¼1
P
i
log½ða
F
þ b
F
xÞða
S
b
S;i
xÞ
¼
X
i¼4
i¼1
P
i
log½a
F
a
S
þða
S
b
F
a
F
b
S;i
Þx b
F
b
S;i
x
2
dlogW
dx
¼
X
i¼4
i¼1
P
i
ða
S
b
F
a
F
b
S;i
Þb
F
b
S;i
2x
a
F
a
S
þða
S
b
F
a
F
b
S;i
Þx b
F
b
S;i
x
2
ð2:52Þ
Below I first present a code to calculate the optimum using equation (2.52) and
secondly, a code which also computes the derivative using the fitness function
directly.
2.9.4.1 Calculating the optimum using equation (2.52)
R CODE (using equation [2.52]):
rm(list¼ls()) # Remove all objects from memory
DERIV <- function(x) # Function to calculate value of derivative
{
Af <-2;Bf<-2;As<- 0.6 # Parameter values
pBs <- c(0.1,0.3,0.4,0.2) # Vector of probabilities for Bs
Bs <- c(0.1,0.12,0.14,0.2) # Vector of Bs values
# Derivative
D <- sum(pBs*(As*Bf-Af*Bs-Bf*Bs*2*x)/((AfþBf*x)*(AsBs*x)))
return(D)
}
# MAIN PROGRAM
uniroot(DERIV,interval¼c(1,2)) # Call uniroot function
OUTPUT: (slightly modified)
$root
[1]
1.545735
$f.root
[1] 1.355284e06
$iter
[1] 4
$estim.prec
[1] 6.103516e05
The optimal body size is at 1.545735
MATLAB CODE: See Section 2.18.17.
2.9.4.2 Computing the derivative using the fitness function directly
An alternative is to use R or MATLAB to calculate the derivative for us and then use
uniroot in R and fzero in MATLAB.
FISHERIAN OPTIMALITY MODELS 103
R CODE:
Note that in FUNC the gradient is the sum of the derivatives over all
four values of Bs.
rm(list¼ls()) # Remove all objects from memory
FUNC <- function(w) # Function to obtain the gradient at a value w
{
Af <-2;Bf<-2;As<- 0.6 # Parameter values
pBs <- c(0.1,0.3,0.4,0.2) # Vector of probabilities for Bs
Bs <- c(0.1,0.12,0.14,0.2) # Vector of Bs values
# Iterate over values of Bs and sum values of derivatives
d <- 0 # Derivative value
for( i in 1:4)
{
Bsi <- Bs[i] # Value of Bs
pBsi <- pBs[i] # Probability of this Bs
y <- deriv(pBsi*log((AfþBf*x)*(AsBsi*x)),“x”) # Get the
deriva-
tive
x <- w # Set x equal to w
z <- eval(y) # Evaluate the derivative at w
d <-dþattr(z,“gradient”) # Assign the gradient value to summed d
}
return(d) # Return d to the main program
}
# MAIN PROGRAM
# Root must be enclosed by the limits set by the user, here set at 1 to 2
uniroot(FUNC, interval¼ c(1,2))$root
OUTPUT:
[1] 1.545735
MATLAB CODE: See Section 2.18.17.
2.9.5 Finding the maximum using numerical methods
This is readily done using the function previously used for plotting. For R we can
use either nlm or optimize.
R CODE:
rm(list¼ls()) # Remove all objects from memory
FITNESS <- function(x){Same code as in plotting function}
# MAIN PROGRAM
nlm(FITNESS, p¼1)
optimize(f¼FITNESS,interval¼c(1,2), maximum¼FALSE)
104 MODELING EVOLUTION
OUTPUT: (slightly modified)
MATLAB CODE: See Section 2.18.18.
2.10 Scenario 8: Continuous temporal variation in
parameters
In the previous scenario the parameter varied in discrete states (four). A more
likely condition is for the parameter to follow a continuous probability distribu-
tion. Applying this to the former scenario we have the following assumptions.
2.10.1 General assumptions
These remain the same as in Scenario 7.
2.10.2 Mathematical assumptions
1. As before, fecundity increases linearly with body size:
F ¼ a
F
þ b
F
x ð2:53Þ
where a
F
and b
F
are constants.
2. Survival decreases linearly with body size:
S ¼ a
S
b
S
x ð2:54Þ
where b
S
varies from generation to generation and is specified by a probability
density function. To avoid undue complexity confusing the approach illustrated
I shall assume the simplest probability function, namely a uniform function,
which is defined as P(b
s
)¼c, where c is determined as explained in Scenario 6.
Parameters values are set at b
max
¼ 0.2 and b
min
¼ 0, giving c ¼ 1/0.2 ¼ 5.
3. As before, the appropriate measure of fitness is the geometric average. For
computational convenience we work with logW:
> nlm(FITNESS, p=1)
$minimum [1] −0.6522457
$estimate [1] 1.545738
$gradient [1] −5.264757e–08
$code [1] 1
$iterations [1] 4
w> optimize(f=FITNESS, interval=c(1,2), maximum=FALSE)
$minimum [1] 1.545735
$objective [1] −0.6522457
FISHERIAN OPTIMALITY MODELS 105

logW ¼
Z
b
max
b
min
Pðb
S
Þlog½ða
F
þ b
F
xÞða
S
b
S
xÞdb
S
¼
Z
b
max
b
min
clog½ða
F
þ b
F
xÞða
S
b
S
xÞdb
S
ð2:55Þ
2.10.3 Plotting the fitness function
Integration is generally more “tricky” than differentiation and not all functions
can be integrated. One also has to be careful that the function exists across the
range of integration. This is potentially problematic in the present model, because
the log of a negative number does not exist and thus we must ensure that this does
not occur. Thus we require the inequality a
S
b
S
x > 0, leading to x<
a
S
b
S
. Using the
limits of b
S
gives x<0.6/0 ¼1and x<0.6/0.2 ¼ 3. There is a symbolic integration
routine in MATLAB, called int but not one in R. Therefore, we shall plot the
function using the numerical integration routine integrate in R, passing to it
the fitness function defined in the function INTEGRAND. A loop is used rather than
apply, because a single value of
x
has to be passed to INTEGRAND.
R CODE (Figure 2.8):
rm(list¼ls()) # Remove all objects from memory
INTEGRAND <- function(Bs,x) # Function todo numerical integration
{
Af <-2;Bf<-2;As<- 0.6; c<- 5 # Parameter values
return (c*log((AfþBf*x)*(AsBs*x))) # return function
}
# MAIN PROGRAM
n <- 100 # Number of points
z <- seq(1.0,3,length¼n) # Create a vector for from 1 to 3
log.W <- matrix(0,n,1) # Create a vector log.W to hold results
Bmin <- 0; Bmax <- 0.2 # Limits of integration
for (i in 1:n) # Iterate over n “body sizes”
{
x <- z[i] # Set value of x (body size)
# Integrate from Bmin to Bmax and add to W
log.W[i] <- integrate(INTEGRAND,Bmin,Bmax,x)$value
}
# Plot fitness¼exp(log.W) vs x
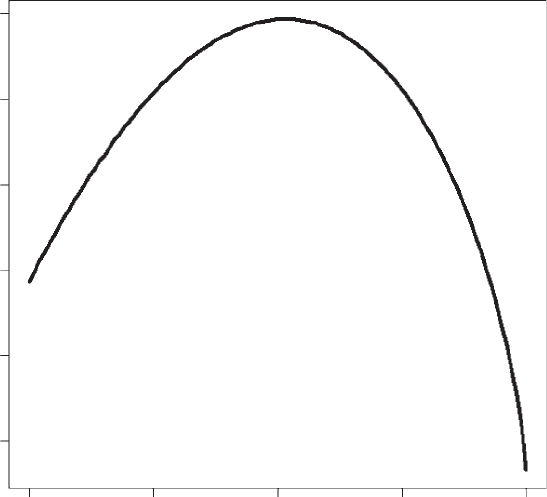
plot(z,exp(log.W),type¼’l’, xlab¼’Body size, x’, ylab¼’Fitness,
W’,las¼1,lwd¼4)
MATLAB CODE: See Section 2.18.19.
106 MODELING EVOLUTION
2.10.4 Finding the maximum using a numerical approach
The main program calls both R functions nlm and optimize (to illustrate that
either can be used) passing to the function the user-supplied function FITNESS
which calls the R function integrate (which does the numerical integration
from b
min
to b
max
), which calls the user-supplied function integrand which
calculates the value of c*log((AfþBf*x)*(AsBs*x)): nlm (and opti-
mize) calls FITNESS calls integrate calls INTEGRAND
R CODE:
rm(list¼ls()) # Remove all objects from memory
INTEGRAND <- function(Bs,x) # Function for numerical integration
{
Af <-2;Bf<-2;As<- 0.6; c<- 5 # Parameter values
return (c*log((AfþBf*x)*(AsBs*x))) # return function
}
# Fitness function integrates over limits
FITNESS <- function(x) # Calculate –log fitness
{
Body size, x
Fitness, W
1.0
1.8
1.9
2.0
2.1
2.3
2.2
1.5 2.0 2.5 3.0
Figure 2.8 Scenario 8: Fitness versus body size.
FISHERIAN OPTIMALITY MODELS 107
