Roff D.A. Modeling Evolution: An Introduction to Numerical Methods

Подождите немного. Документ загружается.

X1 <- uniroot(DFUNC,interval¼(c(0,3)))$root # Call uniroot to

find root

# Calculate x2 for optimum x1

N <- 100; R<- 400 # Parameter values

X2 <- (R/N)-X1 # Size of 2nd propagule

print(c(X1,X2))

OUTPUT:

[1] 2.458153 1.541847

MATLAB CODE:

function y¼DFUNC(x) % Derivative function

% Parameter values

S1 ¼ 0.005; S2 ¼ 0.002; a ¼ 1; N ¼ 100; R ¼ 400;

y¼(S1*exp(-a*x)-S2*exp(-a*(R/N-x))); % Return deriv value

Call function DFUNC with fzero to locate optimum x:

clear all; % Clear the workspace

fzero(@DFUNC,1) % Call root-finding function with initial value at 1

OUTPUT:

ans ¼ 2.4581

2.13.4.2 Getting the derivative using R or MATLAB

R CODE:

rm(list¼ls()) # Remove all objects from memory

# Function to obtain the gradient at a value w

FUNC <- function(w)

{

# Set parameter values

S1 <- 0.005; S2 <- 0.002;a <-1;N<- 100; R <- 400; Fmax<-2

# Get the derivative of equation (2.76)

y <- deriv( N*(S1*Fmax*(1-exp(-a*x))þS2*Fmax*(1-exp(-a*(R/

N-x)))),“x”)

x <- w # Set x equal to w

z <- eval(y) # Evaluate the derivative at w

d <- attr(z,“gradient”) # Assign the gradient value to d

return(d) # Return d to the main program

}

# MAIN PROGRAM

# Root must be enclosed by the limits set by the user, here set at 0 to 3

X1 <- uniroot(FUNC, interval¼ c(0,3))$root

# Calculate x2 for optimum x1

N <- 100; R<- 400 # Parameter values

X2 <- (R/N)-X1 # Size of 2nd propagule

print(c(X1,X2))

118 MODELING EVOLUTION

OUTPUT:

[1] 2.458153 1.541847

As predicted, the optimal size of a propagule in the second clutch is less than that

in the ﬁrst clutch.

2.13.5 Finding the optimum using a numerical approach

Here we use the routine optimize, setting it to ﬁnd the maximum. The ﬁtness

function routine is the same as that used for plotting.

R CODE:

rm(list¼ls()) # Remove all objects from memory

FITNESS <- function(x1){This is the same as given in the plotting section}

# MAIN PROGRAM

# Calculate the optimum x1 using optimize

X1 <- optimize(f ¼FITNESS, interval ¼c(1,8),maximum ¼TRUE)$ maxim um

# Calculate x2 for optimum x1

N <- 100; R<- 400 # Parameter values

X2 <- (R/N)-X1 # Size of 2nd propagule

print(c(X1,X2))

OUTPUT:

[1] 2.458146 1.541854

The results are not exactly equal to the values obtained using the calculus but

certainly close enough.

MATLAB CODE: see Section 2.18.27.

2.14 Scenario 12: The importance of plotting and the utility

of brute force

In the previous scenario we were able to reduce the model to a single trait. We

now examine the same model with the addition of a third clutch. This addition to

the model means that there are two, relatively independent, traits (“relatively,”

because they are free to vary only within speciﬁed limits). In all previous plots

there has been a single, well-deﬁned peak on the ﬁtness surface. In this scenario

the surface turns out to be rugged, such that the optimization routines can get

“stuck” at a point that is not the maximum.

2.14.1 General assumptions

The general assumptions remain as in the previous scenario and so will be omitted

here.

FISHERIAN OPTIMALITY MODELS 119

2.14.2 Mathematical assumptions

1. Given a ﬁxed reserve, R, and an invariant clutch size of N, propagule size is

given by

þ Nx

¼ R ð2:78Þ

where x

is the size of a propagule in the ith clutch (i ¼ 1, 2, and 3).

2. Survival probabilities to the ﬁrst, second, and third clutches are S1, S2, and S3,

respectively, and S1 > S2 > S3.

3. The expected fecundity of offspring from propagules of size x

, F, is given by the

asymptotic function:

max

ð1  e

ax

Þð2:79Þ

where F

max

and a are constants.

4. Fitness, W, is equal to the per generation rate of increase:

W ¼ NS

ð1  e

ax

ÞþNS

ð1  e

ax

ÞþNS

ð1  e

ax

¼ W

þ W

ð2:80Þ

The object is to determine the optimal propagule sizes in the ﬁrst and second

clutches. The size of the third clutch is determined by the allocations to the ﬁrst

two clutches:

ðx

þ x

Þð2:81Þ

As noted previously, Parker and Begon (1986) predicted that under this model

the propagule size in each clutch will be less than in the preceding clutch. For the

present analysis parameter values are set at S

¼ 0.035, S

¼ 0.030, S

¼ 0.025, F

max

¼ 2, a ¼ 1, R ¼ 400, and N ¼ 100.

2.14.3 Plotting the ﬁtness function

Because the total reserve is ﬁxed, the size of the propagules in the ﬁrst clutch is

limited by the inequality x

 R=N or, equivalently, x

N  R: therefore, when this

inequality occurs ﬁtness is set to zero. For the second clutch the propagule size is

limited by the amount remaining after the expenditure on the ﬁrst clutch:

ðx

þ x

ÞN  R. If this inequality is not satisﬁed ﬁtness is equal to the ﬁtness only

from the ﬁrst clutch (assuming that this is greater than zero). A similar constraint

can be applied to the third clutch.

The ﬁtness surface, as shown by the contour plot is rugged and the R commands

do not easily portray it in three dimensions: therefore, for this purpose, I dumped

the data as x,y,W triplets into a text ﬁle and plotted the 3D surface using Sigma-

Plot. Note the use of the R routine expand.grid(x,x), which creates a 2  n

120 MODELING EVOLUTION

matrix of all x by x values, with the ﬁrst column changing most rapidly. Fitness is

then calculated for each row using the R function apply.

R CODE:

rm(list¼ls()) # Remove all objects from memory

FITNESS <- function(x) # Function to calculate fitness

{

# x[1] ¼ Propagule size in 1st clutch

# x[2] ¼ Propagule size in 2nd clutch

# Set parameter values

N <- 100; R <- 400

S1 <- 0.035; S2 <- 0.030; S3 <- 0.025

Fmax <-2;a<- 0.1

W1<-W2<-W3<-0 # Set fitnesses to zero. This is not necessary.

# Check if first clutch mass exceeds reserves

if(N*x[1]>R) W <- 0 # Propagule too large

else{

# Calculate first fecundity

W1 <- N*S1*Fmax*(1-exp(-a*x[1]))

# Calculate size of propagules in 2nd clutch and see if reserves exceeded

if(N*(x[1]þx[2])>R) W <- W1 # Propagules in 2nd clutch too large

else{

W2 <- N*S2*Fmax*(1-exp(-a*x[2])) # Calculate 2nd fecundity

# Calculate the size of Propagules in 3rd clutch

# Note that there must be reserves remaining at this stage

x3 <- (R-N*(x[1]þx[2]))/N

W3 <- N*S3*Fmax*(1-exp(-a*x3)) # Calculate 3rd fecundity

W <-W1þW2þW3

} # End 2nd else

} # End 1st else

return(-W) # Return negative of fitness

}

# MAIN PROGRAM

n <- 20 # Number of rows and columns

x <- seq(from¼1, to¼

5, length¼n)

# Range for propagule sizes

d <- expand.grid(x,x) # Create a matrix of all combinations

W <- apply(d,1,FITNESS) # Apply FITNESS to each combination

W <- matrix(W,n,n) # Convert W from a vector into a matrix

contour(x,x,-W,xlab¼ ’Propagule size in 1st clutch’,ylab¼’-

Propagule size in 2nd clutch’) # Plot contour making W positive

OUTPUT: (Figure 2.12)

FISHERIAN OPTIMALITY MODELS 121

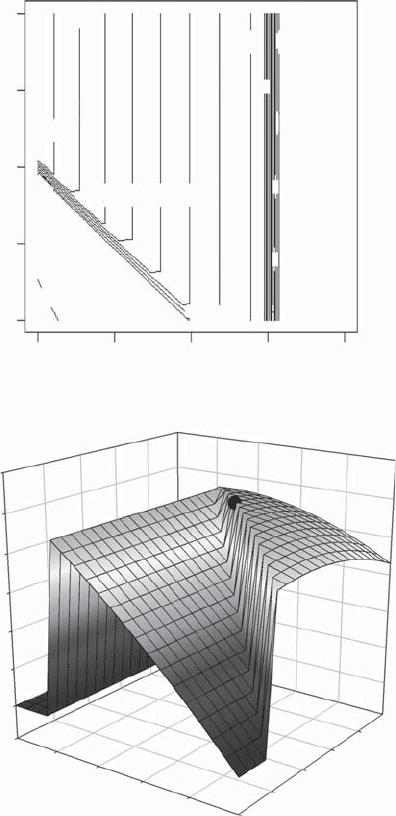
It is evident from the contour and 3D plots (Figure 2.12) that there exists an

optimum value, but it is perched precariously close to, or on the edge of, a

dramatic ﬁtness decline, and there is a large parameter space over which there

is little variation in ﬁtness.

MATLAB CODE: see Section 2.18.28.

Size of propagule in 1st clutch

Size of propagule in 2nd clutch

0.0

0.5

1.0

1.5

2.0

2.5

3.0

Propagule size in 1st clutch

Propagule size in 2nd clutch

2.2

234

0.8

2.2

0.2 0.4 0.6 0.8

1.2

1.4

1.6

1.8

Fitness, W

Figure 2.12 Scenario12: Contour and perspective plots. The dot in the 3D plot shows the

approximate position of maximum ﬁtness. The 3‐D was made using SigmaPlot.

122 MODELING EVOLUTION

2.14.4 Finding the maximum using the calculus

The ﬁrst task is to write the ﬁtness function in a form suitable for partial differen-

tiation with respect to x

and x

. We can do this by substituting equation (2.81) into

equation (2.80):

W ¼ NS

ð1  e

ax

ÞþNS

ð1  e

ax

ÞþNS

1  e

a

ðx

þx

½

ð2:82Þ

At this point we ignore the restriction that Nx

þNx

¼R and proceed with

differentiation

¼ NS

ax

 NS

a



ðx

þ x



¼ NS

ax

 NS

a



ðx

þ x



ð2:83Þ

Setting

¼ 0;

¼ 0 and equating the two equations leads to



þ x

ð2:84Þ

We can substitute the above equation into equation (2.82) to obtain an equation in

, say f (x

) (there is no need here to write out the full equation because it does not

simplify to anything that can be analytically resolved). Now x

is still deﬁned by

equation (2.81) and must exceed zero: thus only combinations of x

and x

that

satisfy this requirement are permitted (i.e., set W ¼ 0 in these cases). Plotting W

versus x

shows that ﬁtness (W) increases with x

until a critical value at which

point W drops to zero due to the allocation exceeding the reserves available. The

optimal propagules sizes can be found numerically using the following code, in

which the code for the ﬁtness function differs somewhat from that used in the

plotting routine instructions. The program seeks the optimal propagule size in the

second clutch using the R function nlm subject to the constraints enumerated

above.

2.14.4.1 Using R or MATLAB to ﬁnd the optima given the differential

This function differs from that used for plotting in that only a single variable,

, is passed. The function FITNESS takes x

as its input, calculates x

using

equation (2.84) and then x

subject to the constraint that x

is positive.

Fitness, W, is calculated according to the rules previously given and –W

returned. The main program uses nlm to locate the optima, using x

as the

input variable. All three trait values are calculated within FITNESS:these

values can b e obtained by simply printing them out w ithin FITNESS or by

writing the results to a ﬁle, which is read back after the optimization is

ﬁnished. To write the data to a ﬁle we must specify the path at the start of

the program: in the present case t his is

FISHERIAN OPTIMALITY MODELS 123

setwd(“C:/Documents and Settings/Administrator/My Documents/

Computer modelling/Chapter 2”)

but the exact path will be user-speciﬁc. To write the data to a text ﬁle called

PROPAGULE.txt we use

write(c(x1,x2,x3), file¼“PROPAGULE.txt”)

and to retrieve the data to a file called Propagules we use

Propagules <- read.table(file¼“PROPAGULE.txt”)

Note that lines are overwritten and so the data ﬁle consists of a single line. To add

lines after the previous lines we need to specify that append is true.

R CODE:

rm(list¼ls()) # Remove all objects from memory

setwd(“C:/Documents and Settings/Administrator/My Documents/

Computer modelling/Chapter 2”) # Set the folder into which to put

the data

FITNESS <- function(x2) # Function to calculate fitness.

# Differs from that used in plotting in only a single variable being

input

{

# Set parameter values

N <- 100; R <- 400

S1 <- 0.035; S2 <- 0.030; S3 <- 0.025

Fmax <-2; a <- 0.1

x1 <- 10*log(S1/S2)þx2 # x1 given the value of x2

x3 <- (R-N*(x1þx2))/N # Value of x3

if (x3<0) W<-0 # Check that x3 exists

else{

# Check if first clutch mass exceeds reserves

if(N*x1 > R) W <- 0 # Propagule too large

else{

W1 <- N*S1*Fmax*(1-exp(-a*x1)) # Calculate first fecundity

# Calculate size of propagules in 2nd clutch and see if reserves

exceeded

if(N*x2 > R) W <- W1 # Propagules in 2nd clutch too large

else{

W2 <- N*S2*Fmax*(1-exp(-a*x2)) # Calculate 2nd fecundity

# Calculate the size of Propagules in 3rd clutch

# Note that there must be reserves remaining at this stage

W3 <- N*S3*Fmax*(1-exp(-a*x3)) # Calculate 3rd fecundity

W <-W1þW2þW3

} # End 3rd else

} # End 2nd else

} # End 1st else

124 MODELING EVOLUTION

# print(c(x1,x2,x3))

write(c(x1 ,x2,x 3), file¼“PROPAGULE.txt”) # Print results into file

return(-W) # Return negative of fitness

}

# MAIN PROGRAM

# Locate optimum x2 and calculate x1 and x3

# Note that parameter values are given within function FITNESS

# Find optimum values of propagules

nlm(FITNESS, p¼1) # Use nlm to find optimum x2

Propagules <- read.table(file¼“PROPAGULE.txt”) # Read in

results

print(Propagules)

OUTPUT: (format modiﬁed slightly)

Here, code ¼ 2, given at the end of the search, means “successive iterates within

tolerance, current iterate is probably solution.” Inspection of the gradient suggests

that it is close to but not exactly at the proper solution. However, given the “cliff

edge” form of the function this is not surprising. As predicted from theory,

propagule size declines across the clutches.

MATLAB CODE: See Section 2.18.29.

2.14.4.2 Using R or MATLAB to do the calculus

The above code assumed that the derivative could be explicitly found. Using the R

function deriv we can get R to evaluate the derivative for us and use this to locate

the optima. Because MATLAB has a symbolic differentiation routine, diff, the

code is somewhat simpler but the conceptual approach remains the same. There

are two user-deﬁned functions.

1. GRADIENT: Finds the absolute difference in the gradient at values w and y,

which in this case are x

and x

. Thus GRADIENT gets the value

AbsDiff ¼j



2. FITNESS: This is the same function as used above except that x

is now

estimated by taking the value of x

and using nlm to ﬁnd the optimum value

of x

by passing to it GRADIENT: the optimum is to be found where AbsDiff ¼ 0.

$minimum [1] −2.388036

$estimate [1] 1.229245

$gradient [1] −0.06119668

$code [1] 2

$iterations [1] 24

> Propagules <- read.table(®le=“PROPAGULE.txt”) # Read in results

> print(Propagules)

V1 V2 V3

1 2.770753 1.229246 9.797043e–07

FISHERIAN OPTIMALITY MODELS 125

After getting the optimum x

the function calculates the value of x

. It then

checks that the values of x

, x

, and x

are permissible values. Finally, ﬁtness, W,

is calculated and its negative value returned.

The main program estimates the propagule size of the second clutch by calling

nlm with FITNESS as the function to be minimized using x

as the variable. Recall

that FITNESS ﬁnds the optimum value of x

given x

: thus nlm within the main

program locates the set of optimum values of x

. As before, the values of x

, x

, and

can be obtained by simply printing them out within FITNESS or by writing the

results to a ﬁle, which is read back after the optimization is ﬁnished.

R CODE:

rm(list¼ls()) # Remove all objects from memory

setwd(“C:/Documents and Settings/Administrator/My Documents/

Computer modelling/Chapter 2”) # Set the folder into which to put

the data

# Function to obtain the gradient at a value w for a given value of y

GRADIENT <- function(w,y)

{

# Set parameter values

N <- 100; R <- 400

S1 <- 0.035; S2 <- 0.030; S3 <- 0.025

Fmax <-2; a <- 0.1

# Calculate derivative, called Dx1x2, with respect to both x1 and x2

# x1 is 1st propagule x2 is 2nd propagule

Dx1x2 <- deriv((N*S1*Fmax*(1-exp(-a*x1))þN*S2*Fmax*(1-exp

(-a*x2)) þN*S3*Fmax*(1-exp(-a*(R/N-(x1þx2))))),c(“x1”,“x2”))

x1 <- w # Set x1 equal to w

x2 <- y # Set x2 equal to y

z <- eval(Dx1x2) # Evaluate the derivative at w

G <- attr(z,“gradient”) # Assignthegradient values to AbsDiff

AbsDiff <- abs(G[1]-G[2]) # Calculate the absolute difference

return(AbsDiff) # Return AbsDiff to the main program

}

# Fitness function given x2, and calling nlm to find x1

FITNESS <- function(x2)

{

# Set parameter values

N <- 100; R <- 400

S1 <- 0.035; S2 <- 0.030; S3 <- 0.025

Fmax <-2; a<- 0.1

# Find value of x1 given x2 using nlm to set derivatives to zero

# This line is the only difference from the previous FITNESS

function

126 MODELING EVOLUTION

x1 <- nlm(GRADIENT,p¼1,x2)$estimate

# Now calculate x3 and fitness

x3 <- (R-N*(x1þx2))/N # Determine x2

if (x3<0) W<-0 # Check if x3 exists(>0)

else{

# Check if first clutch mass exceeds reserves

if(N*x1 > R) W <- 0 # Propagule too large

else{

W1 <- N*S1*Fmax*(1-exp(-a*x1)) # Calculate first fecundity

# Calculate size of propagules

in 2nd clutch and see if re-

serves exceeded

if(N*x2 > R) W <- W1 # Propagules in 2nd clutch too large

else{

W2 <- N*S2*Fmax*(1-exp(-a*x2)) # Calculate 2nd fecundity

# Calculate the size of Propagules in 3rd clutch

# Note that there must be reserves remaining at this stage

W3 <- N*S3*Fmax*(1-exp(-a*x3)) # Calculate 3rd fecundity

W <-W1þW2þW3 # Sum fitness components

} # End 3rd else

} # End 2nd else

} # End 1st else

# print(c(x1,x2,x3))

write(c(x1,x2,x3), file¼“PROPAGULE.txt”) # Print results into file

return(-W)

}

# MAIN PROGRAM

# Find optimum values of propagules

nlm(FITNESS, p¼1) # Use nlm to find optimum x2

Propagules <- read.table(file¼“PROPAGULE.txt”) # Read in results

print(Propagules)

OUTPUT: (format modiﬁed slightly)

$minimum [1] −2.388037

$estimate [1] 1.229246

$gradient [1] 9713.389

$code [1] 3

$iterations [1] 37

> Propagules <- read.table(file=“PROPAGULE.txt”)

> print(Propagules)

V1 V2 V3

1 2.77063 1.229123 0.0002468677

FISHERIAN OPTIMALITY MODELS 127