Roff D.A. Modeling Evolution: An Introduction to Numerical Methods
Подождите немного. Документ загружается.

Previous estimate:
1 2.770753 1.229246 9.797043e-07
In this case, code ¼ 3, meaning that “ last global step failed to locate a point lower
than estimate. Either estimate is an approximate local minimum of the function
or steptol is too small.” The two sets of estimates are very close, the propagule
size in clutch 3 differing somewhat, but either value is so small as to be effectively
zero.
MATLAB CODE: See Section 2.18.29.
2.14.5 Finding the maximum using a numerical approach
Because of the rugged nature of the fitness surface it is possible that nlm (or
fminsearch) will not home in on the appropriate combination. Therefore, in
addition to the use of this function I shall also present an alternative approach, the
“Brute force” method. First, what results do we get using nlm or fminsearch?
2.14.5.1 Using nlm (R) or fminsearch (MATLAB)
R CODE:
rm(list¼ls()) # Remove all objects from memory
FITNESS <- function(x)# Function to calculate fitness
{This function is the same as that used for plotting}
# MAIN PROGRAM
# Call nlm passing fitness function with initial estimates
ANS <- nlm(FITNESS, p¼c(0.1,0.1))
X <- ANS$estimate # Store estimates in X
# Calculate x3
R <- 400; N <- 100 # Parameter values
x3 <- (R-N*(X[1]þX[2]))/N # x3
ANS # Print out Stats for nlm
print(c(X[1],X[2], x3)) # Propagule sizes
OUTPUT: (modified slightly)
$minimum [1] 2.386848
$estimate [1] 2.621084 1.378914
$gradient [1] 2.948550eþ05 2.271604e–02
$code [1] 2
$iterations [1] 32
> print(c(X[1],X[2], x3))# Propagule sizes
[1] 2.621084eþ00 1.378914eþ00 2.299669e–06
Previous results:
1 2.770753 1.229246 9.797043e–07 (using derivatives)
1 2.77063 1.229123 0.0002468677 (using R to get derivatives)
128 MODELING EVOLUTION

The present results differ from the previous results in giving a smaller x
1
and
larger x
2
. Fitnesses calculated at the three estimates, given in the above order, are
2.388, 2.388, and 2.387. Based on the evaluated fitnesses, the first two approaches
are equivalent and the best, followed closely by the numerical approach.
MATLAB CODE: See Section 2.18.30.
2.14.5.2 The Brute force approach
We now consider the “Brute force” approach. From the initial plotting we know
that the optimum occurs within limits of, say, x
1,min
to x
1,max
and x
2,min
to x
2,max
.
Suppose we wish to obtain an estimate that is 0.005: we can try all values within
the foregoing ranges that differ by 0.005. The number of combinations we will
need to try is roughly
x
1;max
x
1;min
0:005
x
2;max
x
2;min
0:005
. Alternatively, we could
simply try a large number of values within the specified range and then, if
necessary, use the resulting output to refine our range. This is illustrated in the
code below where I generate 10,000 combinations. Rather than generate a matrix
to hold W the code below uses the R function expand.grid to generate a two
column matrix called d with the appropriate combinations. In R the routine order
is then used to find the row with the highest fitness.
R CODE:
rm(list¼ls()) # remove all objects from memory
FITNESS <- function(x) # Function to calculate fitness
{This function is the same as that used for plotting, except that W
not –W is returned
return(W) }
# MAIN PROGRAM
# Create vectors to produce an n by n matrix of combinations
n <- 100 # Number of rows and columns
x <- seq(from¼0, to¼5, length¼n)
y <-x
d <- expand.grid(x,y) # Create 2xn
2
matrix of all combinations
W <- apply(d,1,FITNESS) # Use apply to calculate fitnesses
# Now find position of row that has the highest fitness
# Row is stored in first row of Best, Best[1]
Best <- order(W, na.last¼TRUE, decreasing¼TRUE)
x1 <- d[Best[1],1] # Best x1
x2 <- d[Best[1],2] # Best x2
# Calculate x3
R <- 400; N <- 100 # Parameter values
x3 <- (R-N*(x1þx2))/N # x3
print(c(x1,x2,x3,W[Best[1]])) # Propagule sizes and W
OUTPUT:
[1] 2.77777778 1.21212121 0.01010101 2.38771586
FISHERIAN OPTIMALITY MODELS 129
Previous results:
1 2.770753 1.229246 9.797043e–07 (using derivatives)
1 2.77063 1.229123 0.0002468677 (using R to get derivatives)
1 2.621084 1.378914 2.299669e–06 (nlm on fitness function)
Using the brute force results to refine the search (replace with the following lines)
y <- seq(from¼1.0, to¼1.3, length¼n)
x <- seq(from¼2.7, to¼2.8, length¼n)
gives
[1] 2.769697 1.230303 0.000000 2.388037
Fitness at optimum combination:
2.388 (using derivatives)
2.388 (using R to get derivatives)
2.387 (nlm on fitness function)
2.388 (brute force)
2.388 (brute force using first results to shrink ranges)
All methods give essentially the same answer. The one chosen will depend upon
the ease with which the model can be differentiated either symbolically or
numerically. The brute force method is the simplest and guaranteed to work,
even if relatively slow. For this particular model it took only a couple of seconds to
run through the 10,000 combinations. Obviously, as a model gets more complex
the run time will increase and brute force may prove impractical. Nevertheless,
it is certainly worthwhile to keep this approach in mind: it may be crude but it
is very simple and, as shown in the above scenario, it can be very effective.
MATLAB CODE: See Section 2.18.30.
2.15 Scenario 13: Dealing with recursion by brute force
A recursive function is one that calls itself: for example, growth in one year is
typically a function of previous growth, i.e.,W
tþ1
¼ f ðW
t
Þ. Recursive functions can
be particularly difficult to deal with except by the brute force method. To illustrate
a possible approach I shall use a simplified model of the optimal age at first
reproduction and reproductive allocation discussed in Roff et al. (2006).
2.15.1 General assumptions
1. The organism is iteroparous.
2. Reproduction occurs annually.
3. Size in year tþ1 is a function of size in year t.
4. The increment in growth is a function of the allocation to reproduction.
130 MODELING EVOLUTION
5. Annual mortality is a function of the allocation to reproduction.
6. Fecundity increases with the allocation to reproduction.
7. Fitness is a function of reproduction and survival.
2.15.2 Mathematical assumptions
1. In the absence of reproduction the organism increases in weight by a fixed
amount:
W
0
¼ 0
W
1
¼ W
0
þ A
W
2
¼ W
1
þ A ¼ 2A
⋮
W
a1
¼ W
a2
þ A ¼ða 1ÞA
ð2:85Þ
where a is the age of first reproduction. Note that this growth function ceases at
a1, because the allocation to reproduction, described below, occurs during the
year preceding maturation.
2. At maturity a female allocates a constant fraction, G, of its biomass to repro-
duction:
W
tþ1
¼ W
t
þ A GW
t
; t a 1 ð2:86Þ
As noted above, the allocation is made in the year prior to reproduction.
3. Fecundity is proportional to weight and the allocation to reproduction:
F
t
¼ aGW
t
ð2:87Þ
where a is a constant.
4. In the absence of reproduction, the instantaneous (juvenile) mortality rate is M
J
and hence the annual juvenile survival is e
M
j
.
5. The adult mortality rate, M
A
, is a linear function of the allocation to reproduc-
tion:
M
A
¼ M
J
þ M
a
G ð2:88Þ
Where M
a
is a constant. Thus annual survival, commencing in the year immedi-
ately prior to reproduction, is given by e
M
A
¼ e
ðM
J
þM
a
GÞ
.
6. Fitness, W, is the expected lifetime fecundity:
W ¼
X
1
t¼a
aGW
t
e
M
J
ða1Þ
e
M
A
ðtaþ1Þ
ð2:89Þ
The problem we wish to address is that of finding the values of a and G that
maximize fitness. If the recursive equation can be converted into a simple func-
tion the above equation presents no problem, for example, suppose the weight-at-
age function is W
tþ1
¼ A þ BW
t
, then we could write
FISHERIAN OPTIMALITY MODELS 131
W
tþ1
¼ W
1
ð1 e
k
ÞþW
t
e
k
ð2:90Þ
where A ¼ W
1
ð1e
k
Þ and B ¼ e
k
. The above equation is a version of the von
Bertalanffy growth function and it is equivalent to the non-recursive function:
W
t
¼ W
1
ð1e
kt
Þð2:91Þ
The present growth model cannot be reduced to such an equation and hence our
analysis must deal with the recursive form. Given only a few terms it is feasible to
apply the methods of calculus, but if, as in the present case, there are many terms,
such an approach would at best be very tedious. A further problem with a
recursive equation is that the function changes by unit steps, which generally
precludes the use of a search routine such as nlm.
2.15.3 Plotting the fitness function
Even though a changes by unit steps we can still use contour (R or MATLAB) to
plot the computed results: it must, however, be remembered that only integer
values are possible and hence that the correct optimum combination is shifted
relative to the peak portrayed in the contour plot. The summation limit is set to an
age of 30, which calculates fitness to within fractions of a percentage point of its
asymptotic value. Parameter values used are given in the function FITNESS.
R CODE:
rm(list¼ls()) # Remove all objects from memory
# Function to calculate fitness given Alpha
FITNESS <- function(x)
{
G <- x[1] # G values
Alpha <- x[2] # Alpha value
# Set parameter values
Mj <- 0.05 # Background mortality rate
Ma <- 0.4 # Constant of mortality function
Age.max <- 30 # Maximum age (arbitrary)
a <- 0.05 # Fecundity constant
A <- 10 # Wt increase/annum without reproduction
A.minus.1 <- Alpha-1 # Year before first reproduction
S <- matrix(0,Age.max) # Annual survival
# Growth prior to reproduction is linear
# To include cases in which growth is more complex I here use a for
loop
Wt <- matrix(0,Age.max,1) # Initialize Wt vector
S[1] <- exp(-Mj) # Survival to age 1
# Calculate Wt and Survival from age 2 to alpha-1
for(i in 2:A.minus.1)
{
Wt[i] <- Wt[i-1]þ A # Weight
S[i] <- S[i-1]*exp(-Mj) # Annual survival
132 MODELING EVOLUTION
}
# Now calculate change in wt and survival for age alpha to max age
for(i in Alpha:Age.max)
{
Wt[i] <- Wt[i-1]þA-G*Wt[i-1] # Weight
S[i] <- S[i-1]*exp(-(MjþMa*G))# Annual survival
}
W <- a*sum(S[Alpha:Age.max]*Wt[Alpha:Age.max]*G) # Fitness
return(-W) # Return negative of fitness
}
# MAIN PROGRAM
n.G <- 11 # Number of G values
G <- seq(from¼0.01, to¼0.5, length¼n.G) # G vector, 0.01 to 0.5
alpha <- seq(from¼3, to¼20) # Alpha vector from 3 to 20
n.alpha <- length(alpha) # Get length of alpha vector
d <- expand.grid(G,alpha) # Expand to a 2xn.g*n.alpha matrix
W <- apply(d,1,FITNESS) # Calc fitness for each combination
W <- matrix(W,n.G,n.alpha) # Convert to a n.g x n.alpha matrix
# Contour plot
contour(G,alpha,-W, xlab¼“G”, ylab¼“ALPHA”,las¼1,lwd¼3,
labcex¼1)
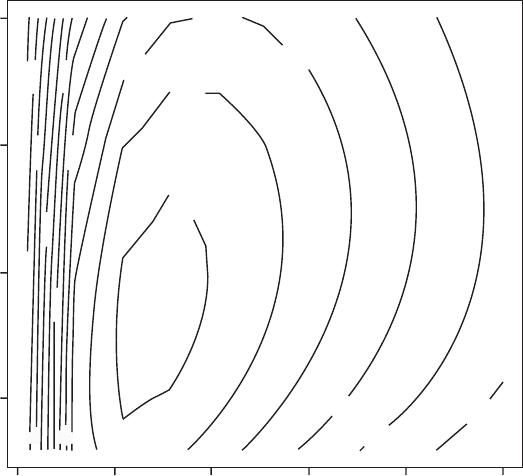
OUTPUT: (Figure 2.13)
G
0.0
5
10
Alpha
15
2.6
2.4
1.4
0.6
0.8
1.8
1.2
1.6
2
1.8
1.6
2.2
2.2
20
0.1 0.2 0.3 0.4 0.5
1
2
Figure 2.13 Scenario 13: Contour plot showing fitness as a function of G and a;.
FISHERIAN OPTIMALITY MODELS 133
Fitness is maximized by combinations at approximately G ¼ 0.12 and a ¼ 10
(Figure 2.13).
MATLAB CODE: See Section 2.18.31.
2.15.4 Finding the maximum using the calculus
This is not a practical method in this case and we move directly to numerical
methods.
2.15.5 Finding the maximum using a numerical approach
The age of first reproduction is an integer and thus it is not possible to use nlm to
find the value of a that maximizes W, but it can be used to find the optimal
allocation for a given a. From the contour plot it is evident that there is a single
peak and hence a simple approach is to begin with a low value of a and increase it
until W decreases below its previous value (code presented at end of section). In
fact, the present model runs so quickly that a simpler approach is to vary a from 3
to 20 and then use the function order to find the best combination.
2.15.5.1 Brute force using many values
R CODE:
rm(list¼ls()) # Remove all objects from memory
# Function to calculate fitness given Alpha
FITNESS <- function(G,Alpha){This function is the same as in the
plotting code, except that G and Alpha are passed rather than x }
# MAIN PROGRAM
# Create vector for alpha values
alpha <- seq(from¼3, to¼20) # alpha vector
n.alpha <- length(alpha) # Length of vector
G <- matrix(0,n.alpha) # Create vector to store best G values
W <- matrix(0,n.alpha) # Create vector to store W values
for ( i in 1:n.alpha) # Iterate over alpha vector values
{
# Find best G for this alpha by calling nlm
G[i] <- nlm(FITNESS,p¼ .2,alpha[i])$estimate # Store best G
W[i] <- -FITNESS(G[i],alpha[i])# Get W at best G for given alpha
}
# Now locate best combination and write out values
Best <- order(W, na.last ¼ TRUE, decreasing ¼ TRUE)
Alpha.best <- alpha[Best[1]] # Best alpha
G.best <- G[Best[1]] # Best G
W.best <- W[Best[1]] # W at best alpha, best G
print(c(Alpha.best,G.best,W.best))
OUTPUT:
[1] 8.0000000 0.1345672 2.6848553
134 MODELING EVOLUTION
MATLAB CODE: See Section 2.18.32.
2.15.5.2 Brute force using iteration
This presumes a single maximum. The strategy here is to compare W at a ¼ t with
W at a ¼ t þ 1 (function ¼ BESTG): if the difference is negative then the maximum
must be at a ¼ t.
R CODE:
rm(list¼ls()) # Remove all objects from memory
# Function to calculate fitness given Alpha
FITNESS <- function(G,Alpha) {This function is the same as in the
plotting code, except that G and Alpha are passed rather than x }
# Function to get best G for consecutive pairs of alpha
BESTG <- function (alpha)
{
# Results for alpha
G1 <- nlm(FITNESS,p¼ .1,alpha)$estimate # Best G given alpha
W1 <- -FITNESS(G1,alpha) # Fitness
# Results for alphaþ1
G2 <- nlm(FITNESS,p¼.1,alphaþ1)$estimate # Best G given
alphaþ1
W2 <- -FITNESS(G2,alphaþ1) # Fitness
Wdiff <- W2-W1 # Diff between fitnesses
return (c(Wdiff,W1,G1)) # G1 will eventually be the best G
}
# MAIN PROGRAM
ALPHA <- 5 # Set initial alpha
DIFF <- BESTG(ALPHA) # Calculate difference between W at two alphas
while (DIFF[1]>0) # If DIFF[1] > 0 then W still increasing
{
ALPHA <- ALPHAþ1
DIFF <- BESTG(ALPHA)
}
# Out of loop and thus ALPHA is the best
print(c(ALPHA,DIFF[3],DIFF[2])) #Print out alpha, G, W
OUTPUT: (same as before)
[1] 8.0000000 0.1345672 2.6848553
MATLAB CODE: See Section 2.18.32.
2.16 Scenario 14: Adding a third variable and more
With two variables it is possible to graphically display fitness as a function of both
variables simultaneously. When the model includes three variables this is no
longer possible. A reasonable approach is to plot two variables, keeping the
FISHERIAN OPTIMALITY MODELS 135
third constant. The general method of analysis is the same as with two variables.
To illustrate this I shall extend the foregoing model to include possible variation in
age-specific allocation to reproduction. I shall assume that the organism lives N
years after maturity. Life history theory predicts that, in general, allocation to
reproduction will increase with age (Roff 2002). We commence by considering the
case of N ¼ 2 and thence more than 2.
2.16.1 General assumptions
1. The organism is iteroparous but survives only 2 years following maturity (N ¼ 2).
2. Reproduction occurs annually.
3. Size in year t þ 1 is a function of size in year t.
4. The increment in growth is a function of the allocation to reproduction.
5. Annual mortality is a function of the allocation to reproduction.
6. The allocation to reproduction is not constrained to be a constant.
7. Fecundity increases with the allocation to reproduction.
8. Fitness is a function of reproduction and survival.
2.16.2 Mathematical assumptions
1. In the absence of reproduction the organism increases in weight by a fixed
amount:
W
tþ1
¼ W
t
þ A; t<a 2 ð2:92Þ
where W
0
¼ 0 and a is the age of first reproduction. This growth function is the
same as previous.
2. After maturity a female allocates an age-specific fraction, G
t
, of its biomass to
reproduction:
W
tþ1
¼ W
t
þ A G
t
W
t
t a 1 ð2:93Þ
Note that, as before, the allocation is made in the year prior to reproduction.
3. Fecundity is proportional to weight and the allocation to reproduction:
F
t
¼ aG
t
W
t
ð2:94Þ
where a is a constant.
4. In the absence of reproduction, the instantaneous (juvenile) mortality rate is M
J
and hence the annual juvenile survival is. e
–M
J
5. The adult mortality rate, M
A
, is a linear function of the age-specific allocation to
reproduction.
136 MODELING EVOLUTION
M
A;t
¼ M
J
þ M
a
G
t
ð2:95Þ
where M
a
is a constant. Thus annual survival, commencing in the year immediate-
ly prior to reproduction, is given by e
M
A
¼ e
ðM
J
þM
a
G
1
Þ
.
6. Fitness, W, is the expected lifetime fecundity:
W ¼
X
aþ1
t¼a
aG
t
W
t
e
M
J
ða1Þ
e
M
A;t
ðtaþ1Þ
ð2:96Þ
2.16.3 Plotting the fitness function
As we have already seen that an optimal combination exists for a G that is not age-
specific and a, it is not necessary here to plot the data.
2.16.4 Finding the maximum using the calculus
This is not practical in this case and we move directly to numerical methods.
2.16.5 Finding the maximum using a numerical approach
As noted previously, the age of first reproduction is an integer and thus it is not
possible to use nlm to find the value of a that maximizes W. From the previous
contour plot it is evident that there is a single peak and this is likely to hold for
variable G, which can be verified by plotting it for several combinations of G
1
, G
2
.
The following code follows the same strategy as previously in beginning with a
low value of a and increasing until W decreases below its previous value. The
fitness function is modified from that given previously as indicated by bold font,
although with slight modification the present code will also work for the previous
case (an illustration that there are generally several ways of coding a program. This
is a good reason to abundantly annotate the code so that one can follow it when
returning after several days, weeks, or months). An important change in the
fitness function is that it now accepts a vector of G values.
R CODE:
rm(list¼ls()) # Remove all objects from memory
# Function to calculate fitness given Alpha
FITNESS <- function(G,Alpha,N) # G IS NOW A VECTOR WITH N ENTRIES
{
# Set parameter values
Mj <- 0.05 # Background mortality rate
Ma <- 0.4 # Constant of mortality function
Age.max <- Alphaþ1 # Maximum age
FISHERIAN OPTIMALITY MODELS 137
