Roff D.A. Modeling Evolution: An Introduction to Numerical Methods

Подождите немного. Документ загружается.

3. While we could use a loop to calculate the summed value for each value of n, a

faster method is the use of the R function apply (whenever possible object-

oriented programming should be used).

4. Finally the results are plotted using the R function plot.

rm(list¼ls()) # remove all objects from memory

# Function to calculate the summation of equation (2.19)

SUMMATION <- function(n)

{

x <- 1 # As before we set x ¼ 1

Age <- seq(from¼1, to¼n) # Sequence from 1 to n

Wt <- 4*x*exp(-(1þ0.5*x)*Age) # Vector of fitness at age t

return(sum(Wt)) # Return the summed value

}

# MAIN PROGRAM

nmax <- 20 # Set maximum value for n

n <- matrix(seq(from¼1, to¼nmax)) # Vector of n values

W <- apply(n,1,SUMMATION) # Apply function SUMMATION to each row

# Plot W vs n using ’l’ to designate a line

# las¼number orientation on axes, lwd ¼ line width

plot(n,W,type¼’l’, xlab¼’Age, n’, ylab¼’Weight, Wt’, las¼1,

lwd¼3)

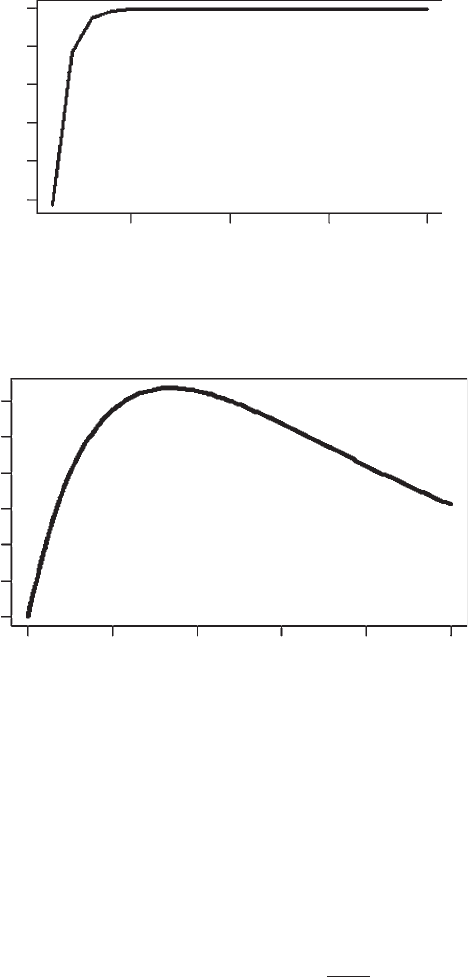
The summation quickly approaches its asymptotic value (Figure 2.2) and setting

the maximum age at 20 should be adequate for all reasonable values of x. Now we

change the summation function to sum for different values of x and plot the result

(Figure 2.3):

rm(list¼ls()) # Remove all objects from memory

# Function to calculate the summation as a function of x

SUMMATION <- function(x)

{

Age <- seq(from¼1, to¼20) # Sequence from 1 to 20

Wt <- 4*x*exp(-(1þ0.5*x)*Age) # Vector of fitness at age t

return(sum(Wt)) # Return the summed value

}

# MAIN PROGRAM

x<- matrix(seq(from¼

0, to¼5

, length¼100)) # Vector from 0-5 of length 100

W <- apply(x,1,SUMMATION) # Apply function SUMMATION to each row

# Plot W vs x using ’l’ to designate a

line

# las¼number orientation on axes, lwd

¼ line width

plot(x,W,type¼’l’, xlab¼’Body size, x’, ylab¼’Fitness, W’,

las¼1,lwd¼4)

MATLAB CODE: See Section 2.18.4.

78 MODELING EVOLUTION

2.5.4 Finding the maximum using the calculus

We are now assured that there is a maximal ﬁtness, we know its approximate

value and can thus set the limits of the search. The summation is, in this case,

solvable and so we shall start by examining the exact solution.

A series that frequently occurs in life history models is the geometric series:

i¼1

i1

¼ 1 þ a þ a

þ a

þ ... ¼

1  a

ð2:20Þ

where |a|<1 (i.e., absolute value of a is less than one). In the present case the

mortality function is a geometric series. For notational simplicity, let a

þ b

x ¼ A

and a

þ b

x ¼ B, which then gives

Body size, x

0.0

0.2

0.4

0.6

0.8

1.0

1.2

12345

Fitness, W

Figure 2.3 Scenario 3: Fitness versus body size.

Age, n

Weight, Wt

0.90

0.95

1.00

1.05

1.10

1.15

10 15 20

Figure 2.2 Scenario 3: Effect of varying length of summation on weight.

FISHERIAN OPTIMALITY MODELS 79

W ¼

t¼1

ða

þ b

xÞe

ða

þb

xÞt

¼ A

t¼1

Bt

ð2:21Þ

To convert this into the form of equation (2.20) we note that e

Bt

can be written as

B

B(t1)

and thus a ¼ e

B

then equation (2.21) becomes

W ¼ A

t¼1

Bt

¼ Ae

B

t¼1

Bðt1Þ

B

1  e

B

ð2:22Þ

We now have a simple function that can be differentiated, although it is a tedious

process and care has to be taken. The derivative using the chain rule (see Appendix

2) is the rather nasty looking equation:

ðb

Þe

ða

þb

xÞ

1  e

ða

þb

xÞ

ða

þ b

xÞ½b

ða

þb

xÞ



1  e

ða

þb

xÞ

ða

þ b

xÞe

ða

þb

xÞ

ð1Þ½b

ða

þb

xÞ



½1  e

ða

þb

xÞ



ð2:23Þ

We need to ﬁnd the value of x at which

¼ 0;, which allows us to simplify the

equation a little since

ða

þb

xÞ

1e

ða

þb

xÞ

is common to all three terms. So the equation we

have to solve is

ðb

Þþða

þ b

xÞðb

Þþ

ða

þ b

xÞð1Þ½b

ða

þb

xÞ



½1  e

ða

þb

xÞ



¼ 0 ð2:24Þ

To solve the above we use uniroot in R and solve in MATLAB.

R CODE:

Define a function FUNC that gives the value of equation (2.24) for a given value of x.

In the main program call uniroot to find the value of x at which FUNC(x) is zero:

# Set up function to be evaluated

FUNC <- function(x){(4)þ(0þ4*x)*(0.5)þ(0þ4*x)*(1)*(0.5*exp

((1þ0.5*x)))/ (1exp((1þ0.5*x)))}

# MAIN PROGRAM

B <- uniroot(FUNC, interval¼ c(0,4))# Find root

B$root # Print out the value found

OUTPUT:

[1] 1.682812

Because we are only interested in positive values the lower limit is set at 0,

excluding the possible negative root. If there were two positive roots the one

80 MODELING EVOLUTION

closest to the lower limit would be given. We know in the present case, from the

plot (Figure 2.3) that there is only a single positive root and hence we do not need

to investigate further.

MATLAB CODE: See Section 2.18.5.

2.5.5 Finding the maximum using a numerical approach

For generality, we shall consider only the summation model.

R CODE:

We use the same summation function as before except that we take the negative

value, because the R function nlm finds the minimum of a function. The function,

nlm requires an initial estimate, p, which here we set at 1:

rm(list¼ls()) # Remove all objects from memory

# Function to calculate the summation as a function of x

SUMMATION <- function(x)

{

Age <- seq(from¼1, to¼20) # Sequence from 1 to n

Wt <- 4*x*exp(-(1þ0.5*x)*Age) # Vector of fitness at age t

return(sum(Wt)) # Return the negative summed value

}

# Main program

nlm(SUMMATION, p¼1)$estimate # Call nonlinear routine nlm

OUTPUT:

[1] 1.682810

MATLAB CODE: See Section 2.18.6.

2.6 Scenario 4: Adding age-speciﬁc mortality that affects the

optimum and using integration rather than summation

In using a summation we are making a statement about when the census is

taken, namely at time steps 1, 2, 3, etc. An alternate assumption is that the

process is more continuous and an integral is appropriate. Reiterating the

assumptions:

2.6.1 General assumptions

1. The organism is iteroparous.

2. Fecundity, F, increases with body size, x, which does not change after maturity

(e.g., as in insects).

FISHERIAN OPTIMALITY MODELS 81

3. Survival, S, decreases with body size, x.

4. Fitness, W, is a function of fecundity and survival.

2.6.2 Mathematical assumptions

1. Maturity occurs at age 1 after which no further growth occurs.

2. Fecundity increases linearly with size at maturity, resulting in fecundity being

a uniform function of age:

¼ a

þ b

x ð2:25Þ

3. The instantaneous rate of mortality increases linearly with the body size

attained at age 1 and is constant per time unit. Under this assumption, survival

to age t is given by

¼ e

ða

þb

xÞt

ð2:26Þ

Note that to make survival a declining function of body size, given the exponential

function, we replace the previous a

b

x with a

þb

4. Fitness, W, is the expected lifetime reproductive success, R

, given as the

cumulative product of survival and fecundity:

W ¼

dt ¼

ða

þ b

xÞe

ða

þb

xÞt

dt ð2 :27Þ

As noted above, we cannot now factor out the age dependent effects from body

size.

2.6.3 Plotting the ﬁtness function

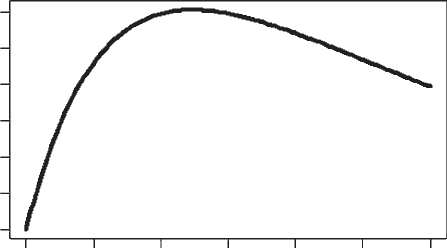
There are two approaches to plotting W versus x: ﬁrst, we could integrate equation

(2.27) exactly to give W as a function of x, and second, we could use a numerical

integration routine. The former is generally to be preferred but integration is

frequently either not possible or extremely difﬁcult. MATLAB has a symbolic

integration routine but R does not.

Noting that

Bt

dt ¼

e

Bt

equation (2.27) can be integrated to give

W ¼ða

þ b

xÞ

e

ða

þb

xÞt

þ b



¼ 0 þ

þ b

ða

þb

xÞ

ð2:28Þ

R CODE (Figure 2.4):

82 MODELING EVOLUTION

We shall use the numerical integration function integrate, passing to it the

function to be integrated in a function which we shall call INTEGRAND, which

contains the expression to be integrated (i.e., ða

þ b

xÞe

ða

þb

xÞt

). Note that the

integration is over Age but that x is also needed. Further, note that because we

have to pass a single value of x we use a loop rather than apply. Parameter values

are Af ¼ 0, Bf ¼ 8, As ¼ 1, and Bf ¼ 0.5.

rm(list¼ls()) # Remove all objects from memory

# Function to do numerical integration

INTEGRAND <- function(age,x)

{

Af <-0;Bf<-8;As<- 1 ;Bs <- 0.5 # parameter values

return ((Af-Bf*x)*exp(-(AsþBs*x)*age)) # return function

}

# MAIN PROGRAM

n <- 100 # Number of points

z <- seq(0,3,length¼n) # Create a vector for z 0 to 3

W <- matrix(0,n,1) # Create a vector W to hold results

for (i in 1:n) # Iterate over n “body sizes”

{

x <- z[i] # Set value of x

# Integrate from 1 to infinity and add to W

W[i] <- integrate(INTEGRAND,1,Inf,x)$value

}

plot(z,-W,type¼’l’, xlab¼’Body size, x’, ylab¼’Fitness, W’,

las¼1,lwd¼4)

MATLAB CODE: See Section 2.18.7.

Bod

size, x

Fitness, W

0.0

0.2

0.4

0.6

0.8

1.0

1.2

0.5 1.0 1.5 2.0 2.5 3.0

Figure 2.4 Scenario 4: Fitness versus body size.

FISHERIAN OPTIMALITY MODELS 83

2.6.4 Finding the maximum using the calculus

Taking the derivative of W with respect to x gives

þ b

ða

þb

xÞ



ða

þ b

xÞb

þ b

ða

þb

xÞ



ða

þ b

xÞb

ða

þ b

xÞ

ða

þb

xÞ

ða

þb

xÞ

þ b

(

ða

þ b

xÞb



ða

þ b

xÞb

þ b

)

ð2:29Þ

This can also be obtained using deriv in R or diff in MATLAB.

R CODE:

y <- deriv((0þ4*x)*exp(-(1þ0.5*x))/(1þ0.5*x),“x”)

y # OUTPUT y

OUTPUT:

expression({

.expr3 <--0þ 4*x

.expr5 <-1þ 0.5 * x

.expr7 <- exp(-.expr5)

.expr8 <- .expr3 * .expr7

.value <- .expr8/.expr5

.grad <- array(0, c(length(.value), 1L), list(NULL, c(“x”)))

.grad[, “x”] <- (4 * .expr7 - .expr3 * (.expr7 * 0.5))/.expr5 -

.expr8 * 0.5/.expr5^2

attr(.value, “gradient”) <- .grad

.value

})

We do not need to interpret the output, merely store it as a variable, say y. To ﬁnd

the value of x at which

¼ 0, we ﬁnd the value of x that makes the components

within {} of equation (2.29) equal to zero.

R CODE:

Two possible routes are shown. In the first the derivative is supplied directly in the

function FUNC, whereas in the second the derivative is obtained in FUNC using the

R function deriv. In either case the main program calls uniroot to find the root:

rm(list¼ls()) # Remove all objects from memory

# Function to evaluate {} in eqn (2.29)

FUNC <- function(x){4þ0.5*(0-4*x)-(0þ4*x)*0.5/(1þ0.5*x)}

B <- uniroot(FUNC, interval¼ c(0,4))# Set lower interval ¼ 0

B$root # Print out the value found

OR using R to obtain the derivative:

# Using R to obtain the derivative

rm(list¼ls()) # Remove all objects from memory

84 MODELING EVOLUTION

# Function to obtain the gradient at a value w

FUNC <- function(w)

{

y<- deriv((0þ4*x)*exp(-(1þ0.5*x))/(1þ0.5*x),“x”) # Get the derivative

x < w # Set x equal to w

z < eval(y) # Evaluate the derivative at w

d < attr(z,“gradient”) # Assign the gradient value to d

return(d) # Return d to the main program

}

# MAIN PROGRAM

# Root must be enclosed by the limits set by the user, here set at 0 to 4

B <- uniroot(FUNC, interval¼ c(0,4))

B$root # Print out the value found

OUTPUT:

[1] 1.236068

In the present scenario we can actually go a step further and ﬁnd an exact

solution. First we place all terms enclosed by {} in equation (2.29) over a

þb

x to

give

ða

þ b

xÞb



ða

þ b

xÞb

þ b

a

 xðb

þ a

Þx

þ b

ð2:30Þ

The numerator is a quadratic equation (ax

þbxþcþ¼0) for which the roots can be

obtained exactly from the standard formula, x ¼

b

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4ac

, which gives 1.236068,

the same as found previously. Notice that the optimum body size, x, is not the

same as found using the summation formula. Whether one uses an integral or a

sum will depend on the biological assumptions. In the present case the integral

model can be more readily solved and thus if there are no strong reasons to prefer

one model over the other then the integral model is clearly the better choice.

Think carefully about the biological assumptions in relation to the ease with

which the model can be solved, but never sacriﬁce necessary biological realism

for mathematical convenience.

MATLAB CODE: See Section 2.18.8.

2.6.5 Finding the maximum using a numerical approach

R CODE:

We use the two R functions integrate and nlm. The function value for a given

age and x, ða

þ b

xÞe

ða

þb

xÞage

, is determined from the user-supplied function

INTEGRAND. Remember that we have to return the negative of fitness, because

we are finding the minimum! To obtain the integral the user-supplied function

FUNC, calls the R function integrate, passing to it INTEGRAND. The optimum x is

found by passing FUNC to nlm:

FISHERIAN OPTIMALITY MODELS 85

rm(list¼ls()) # Remove all objects from memory

# Function to supply components for numerical integration

INTEGRAND <- function(age,x) # Calculate function value

{

Af <-0;Bf<-4;As<- 1 ;Bs <- 0.5 # parameter values

return (-(AfþBf*x)*exp((Asþ Bs*x)*age))# return function value

}

# Function to call integration routine

FUNC <- function(x){integrate(INTEGRAND,1,Inf,x)$value}

# Minimization routine

nlm(FUNC,p¼1)$estimate

OUTPUT:

[1] 1.236067

MATLAB CODE: See Section 2.18.9.

2.7 Scenario 5: Maximizing the Malthusian parameter, r,

rather than expected lifetime reproductive success, R

Thus far we have assumed that the appropriate measure of ﬁtness is the expected

lifetime reproductive success, R

. Whereas this measure of ﬁtness may be appro-

priate for a stable population a more general ﬁtness measure is the Malthusian

parameter, r, which is equal to the population rate of increase at a stable age

distribution:

rt

lðtÞmðtÞdt ¼ 1

t¼1

rt

¼ 1

ð2:31Þ

where l(t), l

are the probabilities of survival to age t and m(t),m

are the age speciﬁc

female births (¼ fecundities/2, assuming an equal sex-ratio). The different nota-

tions used in the two equations are generally of little or no consequence (the

difference equation could equally well have been written in the same manner as

the integral equation) and used here simply to illustrate that differences in nota-

tion should not be taken to imply differences in interpretation. Note that the

difference equation is commenced at the end of the ﬁrst time period, since we

necessarily assume that fecundity is zero at birth (of course we could start from

zero if we simply set m

¼0). Although these equations do not directly encompass

the male contribution we could write a similar equation for males by relating his

mating success to the population growth rate. The assumption underlying the use

of r is that any mutation that increased r would increase in frequency in the

population. This assumption is intuitively reasonable and has been veriﬁed

(Lande 1982; Charlesworth 1994).

86 MODELING EVOLUTION

We shall make the same assumptions as in the previous scenario, except that

the ﬁtness measure will be taken to be r.

2.7.1 General assumptions

1. The organism is iteroparous.

2. Fecundity, F, increases with body size, x, which does not change after maturity

(e.g., as in insect).

3. Survival, S, decreases with body size, x.

4. Fitness, W, is a function of fecundity and survival.

2.7.2 Mathematical assumptions

1. Maturity occurs at age 1 after which no further growth occurs.

2. Fecundity increases linearly with size at maturity, resulting in fecundity being

a uniform function of age:

¼ a

þ b

x ð2:32Þ

3. The instantaneous rate of mortality increases linearly with the body size

attained at age 1 and is constant per time unit. Under this assumption, survival

to age t is given by

¼ e

ða

þb

xÞt

ð2:33Þ

Note that to make survival a declining function of body size, given the exponential

function, we replace the previous a

b

x with a

þb

4. Fitness, W, is the Malthusian parameter r. Taking r to be the measure of ﬁtness,

the ﬁtness function is given by the solution of the characteristic equation:

rt

ða

þ b

xÞe

ða

þb

xÞt

dt ¼ 1 ð2:34Þ

where the initial value of the integral is set at 1, as this is the age of ﬁrst

reproduction.

The two exponents can be absorbed into a single term, giving

ða

þ b

xÞe

ða

þb

xþrÞt

dt ¼ 1 ð2:35Þ

Now the above equation has the same general form as equation (2.28) and so can

be integrated to give

1 ¼ða

þ b

xÞ

e

ða

þb

xþrÞt

þ b

x þ r



¼ 0 þ

þ b

x þ r

ða

þb

xþrÞ

ð2:36Þ

FISHERIAN OPTIMALITY MODELS 87