Robot Millennium (Версия 20.0). Руководство пользователя

Подождите немного. Документ загружается.

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 571 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

где K, M – матрицы жёсткости и масс, соответственно,

- собственный вектор, а

собственное значение. Будет описана процедура эволюции системы базисных векторов

xxx ,...,,

к нижайшей собственной моде. Для минимизации показателя Рэлея применяется

предобусловленный градиентный подход

()

xMx

xKx

(A18)

где

[]

nk ,0∈ , k - номер шага эволюции; 1

n - число базисных векторов, которое

определяет размер подпространства

(

)

span xxx ,...,,

∈

; Nn

1 , где N - число степеней

свободы рассматриваемой задачи (A17). Очень часто оказывается, что рассматриваемая задача

на собственные значения является плохо обусловленной. В таком случае эволюция

последовательности базис-вектора

x к самой нижней собственной моде будет очень

медленной. Оператор предобусловливания

B применяется для улучшения такой ситуации.

Выражение

kkk

zrBz ⇒= означает разрешение данного набора уравнений соответствующего

вектора

z , где B – предобусловливающий оператор, и

kkkk

MxKxr

−

- соответствующий

вектор невязки.

Базис-вектор удовлетворяет следующим условиям ортогональности:

()

npk

,...,2,1,0,,

, =

⎭

⎬

⎫

⎩

⎨

⎧

≠

=xMx (A19)

Исходная крупномасштабная проблема собственных значений (A17) сводится к

проблеме собственных значений подпространства

{

}

{

}

=− qmqk

jiji

(A20)

Матрицы проекции подпространства определены как

{

}

(

)

jiji

k xKx ,

= и

{

}

(

)

UxMx ==

jiji

m ,

, где U - единичная матрица.

Векторы Ритца

121

,...,,

vvv для полученных базисных векторов

xxx ,...,,

соответствующие аппроксимации частот

121

,...,,

ωωω

используются для суперпозиции

динамической характеристики конструкции.

Процедура эволюции базисных векторов

,...,1,0,

x к нижней собственной моде

очень близка к соответствующему шагу итерационного метода предобусловленных градиентов

для решения проблемы собственных значений. Хорошо известно, что сходимость

предобусловленных итерационных методов значительно зависит от свойств

предобусловленного оператора

B . Этот оператор должен быть положительно определённым;

он позволяет получить экономное решение

11 ++

rBz и удовлетворяет числу обусловленности

1)(

αKBC

−

наилучшим возможным способом.

Последнее требование в случае градиентного метода Ритца обеспечивает хорошую

аппроксимацию нижней части собственных мод.

Такой метод применим только для многоуровневого итерационного подхода, который

обеспечивает хорошее качество предобусловливания. Используются как техника

предобусловливания элемент-за-элементом, так и техника ICCF. Качество векторов Ритца,

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 572 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

сгенерированных таким образом, в значительной мере зависит от свойств

предобусловливающего оператора

B (смотри A13 и [8]). Так как модель грубого уровня хорошо

аппроксимирует моды низкой вибрации, векторы Ритца на тонком уровне являются хорошей

аппроксимацией соответствующих главных векторов (смотри [8]). Таким образом, качество

результатов, полученных с использованием этого метода, в значительной мере определяется

способностью модели грубого уровня поддерживать подобие заданной конечно-элементной

модели (так называемый тонкий

уровень). Обычно одиночный аггрегативный уровень

обеспечивает хорошую аппроксимацию. Когда число аггрегативных уровней больше одного,

качество результатов не гарантировано. Это главное ограничение в применении данного метода

для анализа крупномасштабных задач, когда число уравнений превышает ~60000.

Если матрица предобусловливания

B = K (грубый уровень идентичен тонкому уровню),

предложенный градиентный метод Ритца переходит точно в метод Ланцоша (смотри [8]).

Математическое обоснование представлено в [8].

Определение форм колебаний - точность вычислений

Обобщенная проблема собственных значений определена как

0=−

MK , (A17)

где

K, M – матрицы жёсткости и масс, соответственно,

{

}

, - собственные пары (форма

собственных колебаний и собственное значение). Определены два типа векторов невязки:

ϕλϕ

€

MKr −=

(A18)

ϕλϕ

€

MKf

−

−= ,

(A19)

где

{

}

λϕ

€

действительно вычисленные собственные пары, которые содержат некоторые

вычислительные погрешности. Первое выражение определяет остаточный вектор в терминах

сил, а второй - в терминах перемещений.

Четыре различных критерия используются для оценки вычислительной погрешности

собственных векторов.

ϕλε

€

Mr= . Это очень жёсткий критерий. Обычно 01.0≤

означает, что

первые четыре знака в собственном значении вычислены точно. Он применяется только для

метода PCG, когда выбран итерационный алгоритм решения.

()

,r= . Это - слегка более мягкий критерий, чем предыдущий. Он применяется

для модифицированного метода Ланцоша, когда выбран итерационный алгоритм решения.

ϕε

€

/f=

. Это мягкий критерий, потому что сходимость перемещений в данной

реализации МКЭ обычно быстрее, чем сходимость внутренних усилий. Он используется для

методов BLSI, SI и Ланцоша, когда выбраны прямые алгоритмы решения (профильный или

разреженный).

tol

−

λλ

, где

−kk

- два последовательных собственных значения на

шагах итерации k, k-1, а

tol означает допуск для собственных значений, принятый в диалоговом

окне Параметры Анализа Форм Колебаний. Он используется как промежуточный критерий,

когда работают следующие методы: BLSI, SI и Ланцоша (профильный или разреженный

алгоритмы решения) в модальном режиме. Такой критерий неустойчив, однако, он очень

быстрый. Использование (4) позволяет существенно снизить время вычислений для методов

BLSI, SI, Ланцоша, особенно для

крупномасштабных задач. Когда анализ собственных

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 573 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

значений завершён, критерий (3) применяется для окончательной проверки точности.

Пользователь должен обратиться к столбцу “Точность” в таблице, где представлено значение

ϕε

€

/f=

. Если для собственной моды получена недостаточная точность, необходимо

повторить анализ собственных значений с более высоким допуском для собственных значений

tol.

Следующая таблица подводит итог соображений, упомянутых выше. Обозначение Н/О

(не определено) означает, что соответствующая проверка сходимости не выполнена. Результаты

окончательной проверки получены только один раз, и они представлены в столбце “Точность”

таблицы. Проверка сходимости в течение вычислений выполняется несколько раз.

Прямые алгоритмы

решения

Итерационные алгоритмы

решения

Тип

критерия

BLSI,

SI,

Метод

Ланцоша

Ме

тод

сокращени

я базиса

Мод

ифицирован

ный метод

Ланцоша

G_Ritz

PCG

ходе

вычислений

−

λλ

Н/О Н/О Н/

/r=

Окон

чательная

проверка

Н/О

(

Н/

/r=

Следует заметить, что метод Ланцоша для сейсмического режима выполняет проверку

сходимости

ϕε

€

/f=

через каждые 20 шагов Ланцоша. Метод сокращения базиса и метод

PCG_Ritz являются методами Ритца. Так как это – не итерационный подход, проверка точности

не выполняется.

Если точность некоторых форм после вычисления оказывается недостаточной,

необходимо сделать следующее:

Прямые алгоритмы

решения

Итерационные алгоритмы решения

BLSI

SI,

Мето

д Ланцоша

–

модальный

режим

Мет

од

сокращения

базиса

Модифици

рованный метод

Ланцоша

PCG_Ritz PCG

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 574 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

Уме

ньшить

tol из

диалоговог

о окна

Анализ

Форм

Колебаний

Параметры

Увел

ичить число

базисных

узлов и

базисных

направлени

Увеличить

число форм

колебаний;

Уменьшить

tol в диалоговом

окне Параметры

Алгоритм

решения

Увеличить

число форм

колебаний

уменьшить число

аггрегативных

уровней;

Увеличить

число внутренних

итераций

Уменьши

ть

tol в

диалоговом окне

Анализ Форм

Колебаний –

Параметры

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 575 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

Appendix 3C

ПРИЛОЖЕНИЕ 4

Типы Неустойчивости в ROBOT

Типы Неустойчивости, Которые Могут Встретиться При Расчёте Конструкции

Расчёт конструкции может выводить следующие сообщения ‘неустойчивости’:

• тип 1 – элемент с нулевым значением на диагонали матрицы жёсткости

• тип 2 – элемент с нулевым значением на диагонали инвертированной матрицы

жёсткости

• тип 3 – некоторые значения элементов матрицы жёсткости очень

диспропорциональны.

Первый, второй, а иногда и третий тип неустойчивости обычно вызываются

механической неустойчивостью конструкции, например, часть

конструкции представляет собой

механизм, либо параметров опор конструкции (число, тип и место расположения опор)

недостаточно. Третий тип может также встретиться из-за того, что имеются большие различия в

сечениях профилей некоторых элементов.

Все типы неустойчивости могут встретиться в профильном методе решения. Для

фронтального метода могут встретиться только первый и третий

типы. Если сообщение

выводится для фронтального метода, предлагается пересчитать пример с выбором профильного

метода. В случае профильного алгоритма решения число узлов и степеней свободы, в которых

была отмечена неустойчивость, точно указывается.

Итерационные алгоритмы решения не выводят сообщений о неустойчивости, и

неустойчивость модели может приводить к медленной сходимости расчёта. В таком случае

рекомендуется выполнять тщательную проверку модели до вычислений.

Метод решения может быть изменён в диалоговом окне

Настройки Задания (опция

Расчёт Конструкции).

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 576 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

ПРИЛОЖЕНИЕ 5

Расчёт Предельного Равновесия

Нелинейный расчёт предельного равновесия

Введение

Статический нелинейный расчёт предельного равновесия - упрощённый подход,

который позволяет инженеру понять поведение здания в условиях, моделирующих

землетрясение. В текущей версии применены следующие ограничения:

• Все нелинейные свойства, которые определяют возможное разрушение

конструкции при землетрясении, сконцентрированы в так называемых нелинейных шарнирах

предельного равновесия. Другие

нелинейные эффекты (продольные усилия, эффект Пи-Дельта,

стержни тяги-сжатия, и т.п.) могут рассматриваться вместе с нелинейными шарнирами, но они

не играют решающей роли в процессе разрушения конструкций сооружения.

• Нелинейные шарниры могут рассматриваться только для рамных элементов

конструкций и для нелинейных ограничений. Стеновые блоки, смоделированные

оболочечными конечными элементами (КЭ

) и твёрдые тела, не предусмотрены этой опцией.

• Нелинейные шарниры рассматриваются как независимые нелинейные связи для

каждой степени свободы в данном узле. Взаимодействие между различными степенями

свободы игнорируется. Например, изгиб стержня в одной плоскости не зависит от изгиба в

другой плоскости и от продольных усилий. Такое ограничение будет устранено в следующей

версии.

• Расположение каждого нелинейного шарнира определяется пользователем.

Расчёт предельного равновесия состоит из следующих этапов:

• Определить нелинейные шарниры в расчётной КЭ схеме.

• Присвоить нелинейные свойства шарнирам (диаграммы усилие-смещение или

момент-поворот)

• Выполнить расчёт форм колебаний для активации матрицы масс (1 формы

достаточно).

• Определить калибр поперечных сил. Примечание: Поперечные

силы толчка

зависят от типа матрицы масс.

• Назначить контрольный узел и направление, и предельное значение перемещения

от толчка (когда смещение в контрольном узле и направлении превышают такое пороговое

значение, нелинейный расчёт заканчивается).

• Назначить параметры нелинейного расчёта.

• Провести нелинейный расчёт шаг-за-шагом. В результате нелинейного расчёта

будет получена кривая

равновесного состояния “перерезывающие силы против контрольного

смещения ” V = V(D). Перерезывающие силы определяются как сумма реакций для заданного

направления толчка, вызванные соответствующим калибром поперечного усилия.

• Преобразовать кривую равновесного состояния V = V(D) в формат ADRS

(спектры реакции ускорения смещения) – построить график несущей способности

)(

cap

SSS = , где

cap

S - спектральное ускорение и SB

B – спектральное смещение.

• Выполнить сглаживание кривой несущей способности. Сглаженная кривая

несущей способности используется для расчёта предельной выносливости.

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 577 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

• Рассмотреть уменьшение периода вибрации вследствие гистерезисного

демпфирования, вызванного существенно нелинейными деформациями конструкции.

Конвертировать кривую несущей способности в ось “эффективное демпфирование против

периода” )(

effeff

= .

• Выполнить пошаговый поиск точки предельной выносливости как точки

пересечения кривой несущей способности )(

cap

SSS = и выбранной кривой запроса.

Определение поперечной нагрузки

Как это часто имеет место для трёхмерных конструкций, первая форма колебаний

вызывает местную вибрацию небольшой части конструкции (местные колебания одиночного

или нескольких стержней, локальная форма пластины, и т.д.). Такой вид вибрации обычно не

показательный для анализа сейсмической реакции, так как он

даёт малый вклад в сейсмическое

движение (его модальный процент масс невелик). Поэтому следующий алгоритм применяется

для подготовки моды толчка – вектора формы, который предопределяет вектор смещения при

расчёте предельного равновесия. В общем, дальнейшие соображения базируются на [2] с

частичной адаптацией к машинной реализации.

•

dirdirdir

I Φ⇒=Φ

MK , где K, M – матрицы жёсткости и масс, соответственно, IB

dir

B –

унитарный вектор направления (в случае которого единицы располагаются на местах

поступательных перемещений в направлении dir = x ↔ y,z, тогда как на всех других местах

располагаются нули; x, y, z – направления давления); Φ

dir

B принимается как мода толчка.

• Нормализовать моду толчка:

dirdir

Φ=Φ

, где

(

)

dirdir

ΦΦ=

• Коэффициент участия масс:

(

)

dirdirdir

• Отыскивать поперечные силы в виде:

dirdirdir

, где γB

dir

B – скалярный

множитель. Перерезывающая сила

(

)

(

)

dirdirdirdirdirdirdirdir

IIFV Γ

,, M .

Поэтому

dir

dirdir

dir

VF ∗Φ

= M

. Условимся считать, что V

dir

B=1 как VB

dir

играет роль параметра нагрузки в нелинейном расчёте предельного равновесия, и только

объёмный калибр поперечных сил представляет для нас интерес в настоящий момент. Таким

образом,

dir

F Φ

= M

. В следующей части индекс dir будет игнорирован, поскольку каждое

направление толчка требует специального расчёта предельного равновесия.

Кривая Равновесных состояний. Нелинейный алгоритм.

Характеристики нелинейных шарниров обычно сложны (смотри [1,2]) и содержат ветви

деградации. Это часто вызывает пилообразную форму кривых равновесного состояния. Для

преодоления этих затруднений применяется алгоритм длины дуги. Появляется диалоговое окно

расчёта предельного равновесия.

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 578 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

Рис. 10.5.1 Параметры расчёта предельного равновесия: Число узлов, направление –

число узлов и направление, установленное для контрольного смещения; Максимальное

смещение – это максимальное значение контрольного смещения от толчка; Параметры

нелинейности – смотри нелинейный расчёт.

Если отмечены флажки Нелинейный анализ или P-дельта, тогда нелинейные свойства

каждого конечного элемента принимаются во внимание в дополнение к нелинейным

шарнирам.

В противном случае только нелинейные шарниры и другие специфические нелинейные

элементы (тяги-распорки, нити и нелинейные связи) определяют нелинейные свойства

конструкции.

Кривая несущей способности. Формат ADRS

Таким образом определяется кривая равновесного состояния V = V(D), где V –

перерезывающая сила, а D – управляющее смещение. Следующий шаг – сходимость

равновесных состояний V = V(D) к так называемому формату спектра реакции ускорение-

смещение

(ADRS): )()(

cap

SSSDVV =⇒= , где SB

B, SB

B – спектральное ускорение и

спектральное смещение. Функция )(

cap

SSS = является спектром несущей способности.

Процедура преобразования состоит в следующем: для каждой точки {D,V} ∈ V = V(D)

отыскивается соответствующая точка для спектра несущей способности

{}

)(,

cap

aad

SSSSS =∈ с использованием формулы

tot

===

αα

(10.5.1)

где

tot

- процент масс для моды толчка,

(

)

dirdir

dir

tottot

IIMM ,M== - общая масса

конструкции; W – вес конструкции; g – ускорение силы тяжести.

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 579 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

ΓΦ

= , (10.5.2)

где Φ

B – такой компонент вектора моды толчка Φ, который соответствует (ему

назначены те же узел и направление) управляющему смещению D.

В общем, V = V(D) обычно нелинейная функция. Уравнение )(

cap

SSS = также

является нелинейной функцией (смотри Рис.10.5.2). Каждая точка на такой кривой

ассоциируется с периодом T. Эволюция нелинейных деформаций приводит к изменению

периода свободных колебаний. Очевидно, что T=const на диаграмме ADRS представляет собой

прямую линию, проходящую через начало координат. Поэтому для всех точек линейной части

спектра несущей способности период один и тот же, и

обозначается он TB

lin

B. Это значение

основано на решении линейной системы уравнений

KXB

dir

B = FB

dir

B, где K – матрица жёсткости,

описывающая линейные свойства конструкции, а F

dir

B - калибр поперечных сил. Введём

обозначение: D

lin

B – компонент вектора решения XB

dir

B, для которого степень свободы – такая же,

что и для управляющего смещения D; V

lin

B – сумма реакций (перерезывающая сила), вызванных

действием F

dir

B. Согласно [2],

(10.5.3)

После подстановки (10.5.1), (10.5.2) в (10.5.3) получаем:

Dlin

lin

(10.5.4)

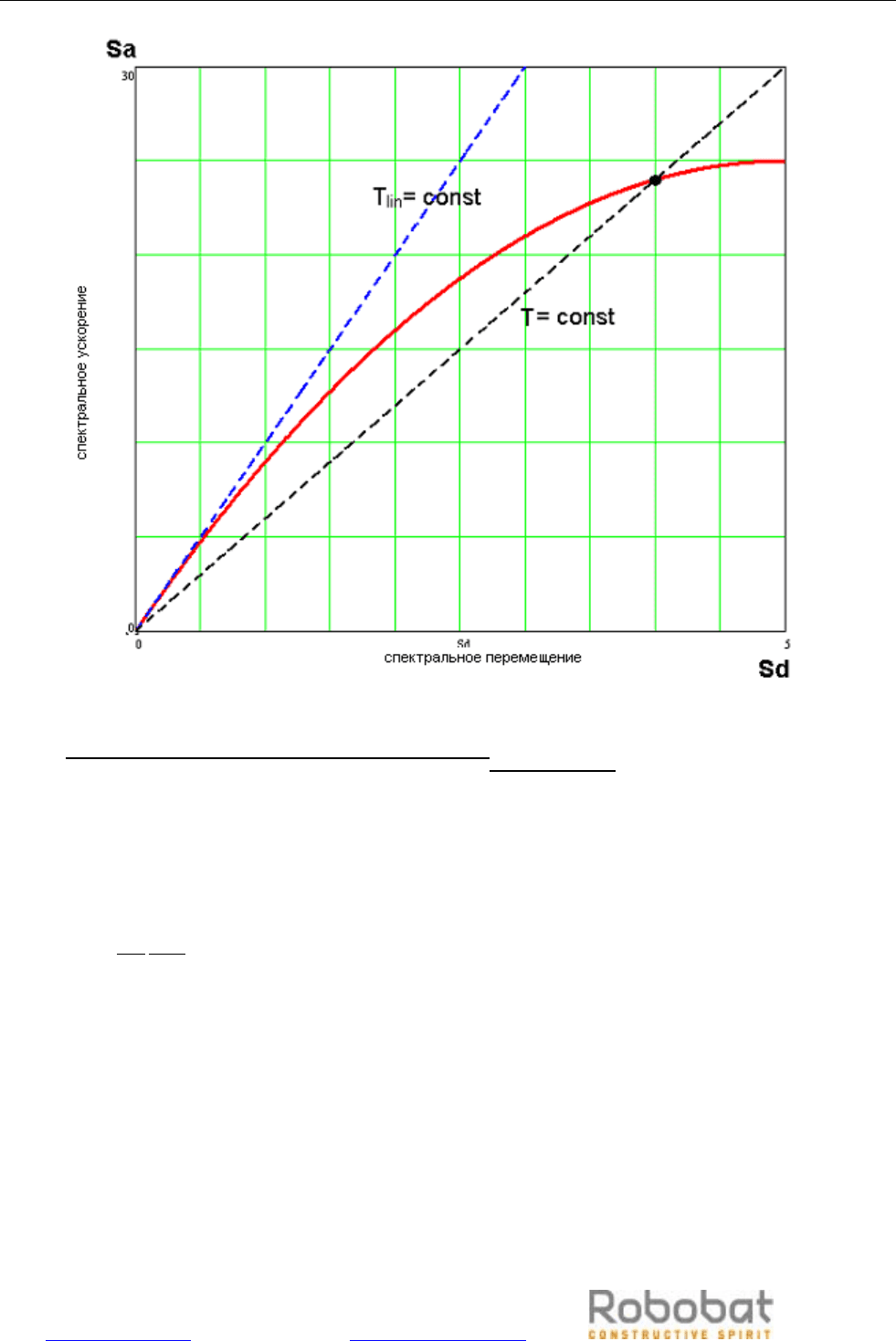
ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 580 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

Рис. 10.5.2 Спектр несущей способности в формате ADRS

ГИСТЕРЕЗИСНОЕ ДЕМПФИРОВАНИЕ. КРИВАЯ )(T

effeff

Появление неупругих деформаций вызывает гистерезисное демпфирование.

Соответствующие области, показанные на Рис. 10.5.3, иллюстрируют энергию, рассеянную за

цикл, и максимальную работу деформации. Если вибрация данной системы связана с вибрацией

системы одиночных степеней свободы с вязкостным демпфированием, то эквивалентное вязкое

демпфирование за полную петлю гистерезиса - следующее:

= , (10.5.5)

где: E

B – энергия, рассеянная за цикл; EB

B - максимальная работа деформации. Энергия,

рассеянная за цикл E

B, и максимальная работа деформации EB

B могут быть определены,

основываясь на рассмотрении Рис. 10.5.3:

⎟

⎠

⎞

⎜

⎝

⎛

∆−=

∫

daD

ABKAreadSSE

)(4; )(

OABAreaE

∆

(10.5.6)

Эффективное демпфирование определяется как:

05.0

eff

(10.5.7)

где: 0.05 – вязкостное демпфирование, κ - коэффициент, принятый по [2] согласно Рис.8-