Robot Millennium (Версия 20.0). Руководство пользователя

Подождите немного. Документ загружается.

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 561 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

нелине ыражены слабо, такое приближение оказывается корректным. В

противном случае необходимо решать нелинейную статическую задачу (3.11.8) (этот метод не

освещается настоящим Руководством). Очевидно, что линейный подход (3.2.17) быстрее, чем

нелинейный (3.11.8). В случае линейного подхода, выходит так, что

йные эффекты в

()

GGK

= )x(x

ststs

, где G

– матрица геометрической жёсткости.

2. Анализ собственных значений (3.12.6)

Известно, что положительные значения

) представляют состояния

устойчивого равновесия, негативные значения

) – неустойчивого, в то время как

нулевые значения

) соответствуют потере устойчивости (выпучиванию).

Потеря положительной определённости матрицы

(0>

(0<

(0=

(

)

sts

означает, что статическая

нагрузка превысила свой критическое значение (выпучивание). Появляется соответствующее

сообщение. Сходимость будет утрачена во время решения нелинейной статической задачи

(3.11.8). Рекомендуется прервать вычисления, так как последующие вычисления будут лишены

смысла.

Только нелинейный подход применим для конструкций, содержащих гибкие нити и

элементы, работающие на растяжение-сжатие.

ример

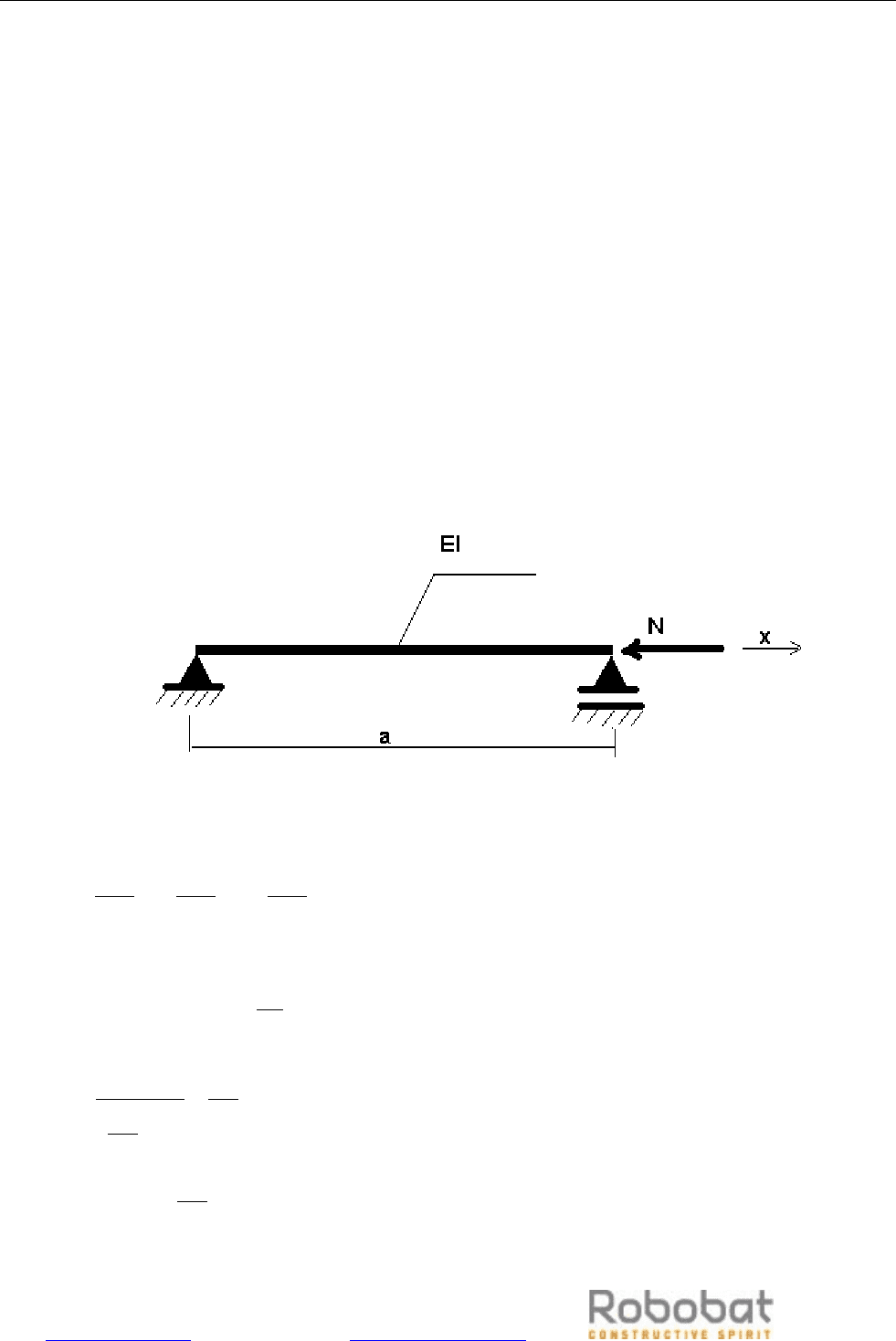
ассмотрим пример, представленный на рисунке ниже.

Рис. 3.11.1

Здесь

N - статическая нагрузка. Поведение такой системы описывает следующее

уравнение:

∂

, ( 3.11.9 )

где w – изгибное смещение,

- плотность материала, F – площадь поперечного сечения.

Будем отыскивать решение в виде:

()

⎟

⎠

⎞

⎜

⎛

Wetxw

sin,

⎝

( 3.11.10 )

осле подстановки ( 3.11.10 ) в ( 3.11.9) получаем: П

⎟

⎞

⎜

⎛

, ( 3.11.11 )

−

⎠⎝

где

⎟

⎠

⎜

⎝

- критическая нагрузка,

⎞

⎛

- собственное значение для N = 0

(результат обычного Анализа форм колебаний). Окончательно,

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 562 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

−= 1

ωω

, ( 3.11.12 )

где

- собственное значение для системы, подверженной действию статической

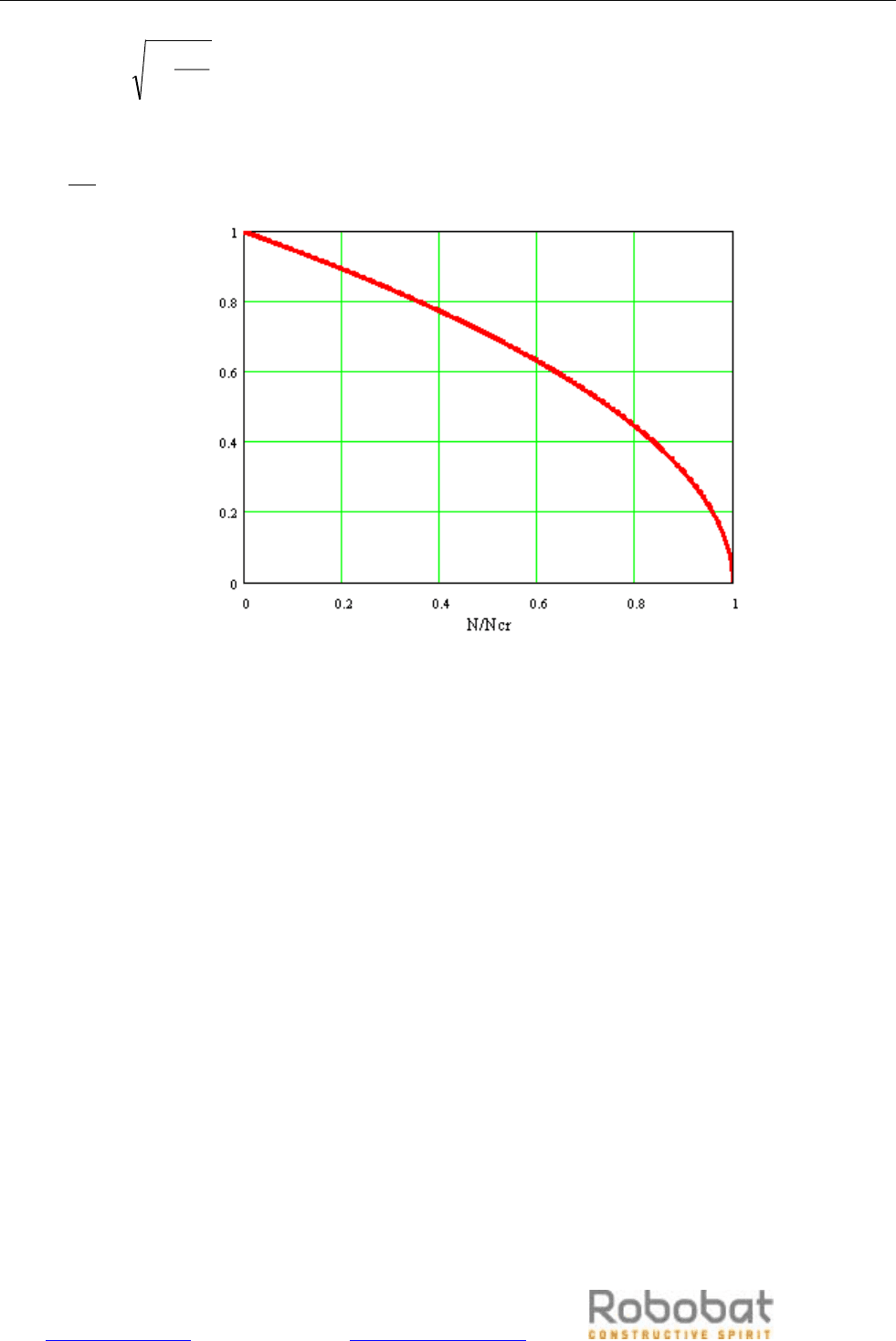
нагрузки N. Этот результат представлен в графическом виде на Рис. 3.11.2:

Рис.3.11.2

а исимость

()

= , где

З в

- параметр нагрузки, для реальной конструкции обычно

более с жнало я, чем представленная выражением ( 3.11.12 ) (смотри [ 1,22 ]).

Приложение 3A

етоды решения проблемы собственных значений М

Пользователь должен понимать, что на данный момент “лучший универсальный метод”

решения задач на собственные значения не существует.

=Φ−Φ

iii

, i=1,2,…,n ( A1 )

где K - м а масс,

атрица жёсткости, M – матриц

- собственная мода, и

- пульсация.

Термин “наиболее предпочтительный” означает, что для большинства задач такой метод будет

использовать наименьший объём ресурсов (время расчётов и объём жёсткого диска) в

сравнении с любым другим. Однако, это не исключает иных ситуаций в случае других задач.

Тогда ется примерекоменду нение другого метода. Настоящая версия ROBOT предлагает

несколько методов решения обобщённой проблемы

собственных значений (A1). Каждый из них

имеет достоинства и недостатки. Ниже представлены некоторые рекомендации, которые

следует учесть при выборе метода анализа. Мы надеемся, что в большинстве случаев они

приведут к желаемым результатам наилучшим образом.

Метод итерации подпространства (SI) реализован точно так, как описано в [4], поэтому

описание этого метода здесь не приводится.

Метод

Ланцоша

Ланцоша [12,16,17] – мощный, устойчивый подход, используемый для решения

крупномасштабных проблем собственных значений (A1). Он применим, когда выбраны прямые

алгоритмы решения (профильный или разреженный).

свои

Метод

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 563 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

Этот подход позволяет получить первых n собственных значений и собственных мод с

желаемой точностью. Преимущества метода Ланцоша становятся тем значительней, чем

большее число требуемых собственных пар получено. Однако, этот подход имеет несколько

ограничений, а именно:

Трёхдиагональная матрица T не должна быть разложена. Это означает, что невозможно

анализировать конструкцию, состоящую из двух или более

несвязанных подструктур. В таком

случае либо каждая подструктура рассматривается отдельно, либо применяется другой подход

(например, методы блочной итерации подпространства (BLSI) или сокращения базиса).

Матрица масс M должна быть принята как “ Сосредоточенная с Вращениями” или

“Консистентная”.

Нулевая плотность не допускается.

Метод Ланцоша использует приведение к трёхдиагональной метрице T

, ( A2 )

где

MQMKQT

1−

{

}

qqq

,...,,

“Ланцоша”,

- прямоугольная матрица Neq x j, а Neq – число уравнений, j –

число шагов

- j-ый вектор Ланцоша. Выражение

jjjjjjj

qqqq

βαβ

−−=

−

( A3 )

генерирует следующий вектор Ланцоша

1+j

, и определяет текущую строку матрицы T

αβ

βαβ

βα

•••

433

322

Таким образом, получается следующая сокращённая проблема собственных значений:

0=−

T , k=1,2,…,j ( A4 )

, где это j-ое приближение к , k=1,2,…,n, n – требуемое число

собственных пар. Алгоритм будет продолжать вычисления (для увеличения j – числа шагов

Ланцоша), пока требуемая точность не будет достигнута для всех требуемых собственных

значений.

Процедура выборочной ортогонализации поддерживает требуемый уровень

ортогональности между векторами Ланцоша

()

λω

, которая обеспечивает надёжность и численную

устойчивость вычислительного процесса. Мы используем экономные методы для обеспечения

выборочной ортогонализации и для решения сокращённой задачи на собственные значения

(A4) методом двойной QR-итерации со сдвигами.

Исходные собственные векторы определяются по следующей формуле

Q=Φ , k=1,2,…,n ( A5 )

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 564 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

Подробности представлены в [12,16,17].

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 565 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

ия базиса

[4,5] известен как улучшенный метод Рэлея-Ритца [4]. В [5]

такой м ант метода Бубнова-Галёркина. Он применим для

прямы я (профильного и разреженного). Этот алгоритм позволяет получить

приближённые значения первых нескольких собственных пар. Необходимо назначить ведущую

степен получить редуцированную (сокращённую) систему. Таким

образо

румент для пользователей, которые имеют определённый опыт динамического расчёта

констр кций и работают с теми видами конструкций, поведение которых известно. Этот метод

позволяет исключить нежелательные степени свободы (DOF) из сокращённой модели и

привести исходную сложную задачу с большим числом степеней свободы к сокращённой

форме – со значительно меньшим числом

степеней свободы. Опыт динамического расчёта

констр кций показывает, с какими проблемами может встретиться пользователь, когда «методы

автоматической редукции» (имеются в виду методы SI, BLSI и Ланцоша) приводят к очень

сложному процессу вычислений. Например, формы местной вибрации одиночных стержней

могут привести к серьёзным проблемам для этих методов, поскольку они отыскивают

автома твенные пары без

никакого отбора. Следует заметить, что для большинства

случае связями, не принимаемыми во

вниман одели, либо их вклад в общее движение системы будет

несущ чно процент масс для таких местных вибраций очень мал. Использование

“точны т к вышеупомянутым

затруднениями, однако,

примен метода сокращения базиса может значительно упростить

вычисл

ие ограничения.

: ведущие узлы и

ведущ щения (не вращения) могут быть назначены в

качест ы.

ого типа матрицы масс, однако

, тип матрицы масс

“Сосре ащений” является наиболее выигрышным в отношении времени

вычислений.

на. Имеется только один способ

исслед чить число ведущих степеней свободы

(назначить дополнительные ведущие узлы и ведущие направления), решить эту задачу снова и

сравнить собственные значения.

Такой метод преобразует

исходную крупномасштабную задачу для МКЭ-модели (A1)

Метод сокращен

Метод сокращения базиса

етод представлен как дискретный вари

х алгоритмов решени

ь свободы (MDOF), чтобы

м, пользователь может контролировать

создание сокращённой модели. Это мощный

инст

тически собс

в эти местные вибрации будут ограничены некоторыми

ие в конечно-элементной м

ественным. Обы

х” методов в таком случае приведё

ение приближённого

ительный процесс.

Этот метод имеет следующ

1. Пользователь должен назначить ведущую степень свободы

ие направления. Принято, что только сме

ве ведущих степеней свобод

2. Алгоритм применим для люб

доточенная без вр

3. Проверка последовательно Штурма недоступ

овать сходимость проверки, а именно, увели

=Φ−Φ

iii

(A6)

в задачу на собственные значения для редуцированной модели

{} {}

=−

αωα

mf (A7)

где {f} – матрица влияния, {m} – обобщённая матрица масс для редуцированной модели,

...

, (A8)

∑

≈Φ

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 566 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

где n – число степеней свободы редуцированной модели. Базис такого преобразования –

статическое решение, полученное для подходящих единичных состояний: единичные узловые

нагрузки прикладываются последовательно в каждом ведущем узле, в выбранном ведущем

направлении. Крупномасштабная статическая задача решается для n правых частей:

=K (A9)

где

ni ,...,2,1=

- вектор нагрузки, соответствующий i –ой единичной нагрузке. Пользователь

должен назначить ведущие узлы и ведущие направления. Все требуемые действия будут

выполнены программой.

Редуцированная задача на собственные значения решается методом Якоби, что приводит

к приближённым частотам

, и формам колебаний

∗

, i=1,2,…,n. Подробности этого подхода

представлены в [5].

Метод блочной итерации подпространства

Метод блочной итерации подпространства (BLSI) разработан для решения обобщённой

проблемы собственных значений (A1). Он применим для прямых алгоритмов решения

(профильного и разреженного). Это мощный, устойчивый подход. Применение этого метода

настоятельно рекомендуется, когда встречается крупномасштабная задача, и необходимо

получить большое число собственных пар (больше 10). Метод BLSI может применяться для

расчёта отдельных конструкций. При анализе

форм колебаний применимы все типы матрицы

масс (“Сосредоточенный без вращений”, “Сосредоточенный с вращениями” и

“Консистентный”). Область применения этого подхода ограничена модальным режимом.

Сейсмический режим и псевдо-режим по-прежнему применимы, если выбран метод Ланцоша.

Проверка последовательности Штурма выполняется для обнаружения пропущенных

собственных значений. Метод BLSI управляет непрерывностью сходящихся собственных

значений. Разрывность

сходящихся собственных значений указывает на присутствие

пропущенных собственных значений. Однако, непрерывность сходящихся собственных

значений не обеспечивает твёрдой уверенности в отсутствии пропущенных собственных

значен

м шаге итерации.

рименение процедуры ускорения сдвига [1,4] рекомендуется в процессе анализа форм

колебаний, когда наблюдается медленная сходимость:

ий. Тем не менее, опыт многочисленных расчётов показывает, что во многих случаях

проверка последовательности Штурма не обнаруживает пропущенных собственных значений,

когда метод BLSI обеспечивает непрерывность сходящихся собственных значений. Таким

образом

, большим преимуществом такого метода является возможность избежать трудоёмкой

процедуры проверки Штурма, если не требуется полной гарантии отсутствия пропущенных

собственных частот. Если встречается разрывность сходящихся собственных значений,

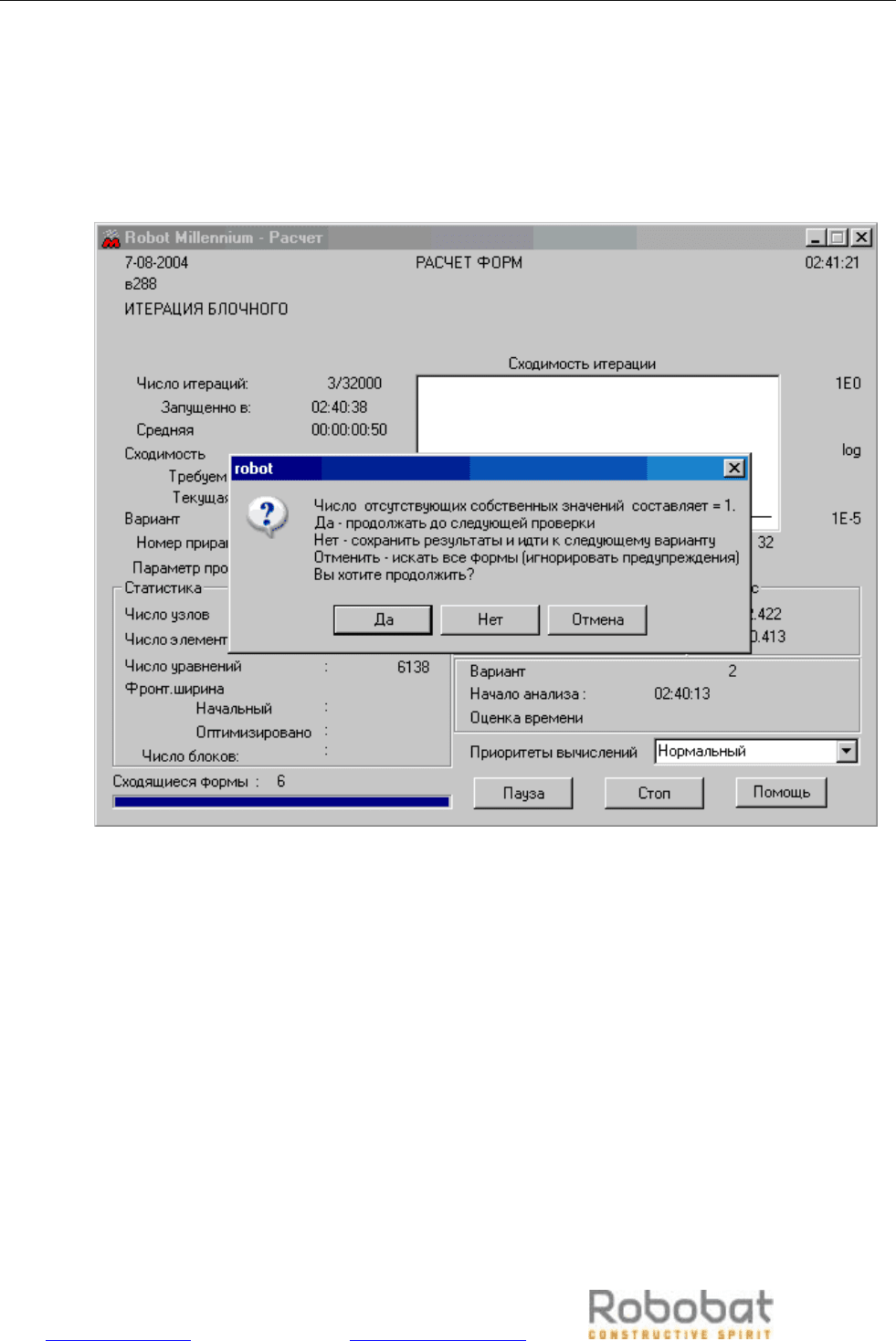
появляется соответствующее сообщение (смотри Рис A1).

Главная идея метода BLSI [1-3] состоит в одновременных итерациях векторов в

подпространстве фиксированного размера. Каждый сходящийся вектор удаляется из “рабочего”

подпространства (

блока), а взамен его добавляется новый стартовый вектор. Ортогональность

сходящихся векторов обеспечивается на каждо

=Φ−Φ

, ( A10 )

где

MKK

−=

, σ - значение сдвига. В начале анализа принимается σ = 0. Значение

сдвига обновляется автоматически, если новые сходящиеся собственные значения не

появляются через принятое число шагов контролируемой итерации. Например, пусть принято

число онтрольных шагов равным 5. Затем 5 сходящихся собственных значений появляются

после 4 итераций. Значение сдвига остаётся σ = 0. На следующем шаге итерации 3 собственных

значения сходятся.

Значение сдвига остаётся σ = 0. Затем на протяжении 5 итерационных шагов

ни одна из собственных мод не сходится. Алгоритм опять обнаруживает “медленную

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 567 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

сходимость”, принимает , обновляет

ωσ

MKK

−

и факторизует обновлённую

матрицу сдвига

. Затем после 2 шагов итераций сходится 2 собственных моды. Значение

сдвига остаётся

. Затем в течение следующих 5 шагов итераций ни одно из собственных

значений не Алгоритм снова обнаруживает “медленную сходимость” и принимает

, обновляет

ωσ

сошлось.

ωσ

MKK

−

и факторизует обновлённую матрицу со сдвигом И так

далее.

Рис. A1 Разрывность сходящихся собственных значений обнаружена при работе метода

BLSI. Да – вычисления будут продолжены до появления следующего сходящегося

собственного значения. Впоследствии очередная проверка будет выполнена.

Нет – результаты будут сохранены, и вычисления будут проводиться для следующего

случая.

Отменить – вычисления продолжаются до тех пор, пока обеспечивается полная

непрерывность сходящихся собственных значений. Предупреждения будет

игнорироваться.

Это - не все рекомендации: применить ускорение сдвига или не делать этого.

Пользователь должен помнить, что применение подходящего сдвига является самым мощным

инстру ентом ускорения сходимости. Иначе каждая факторизация обновлённой матрицы

мо н х

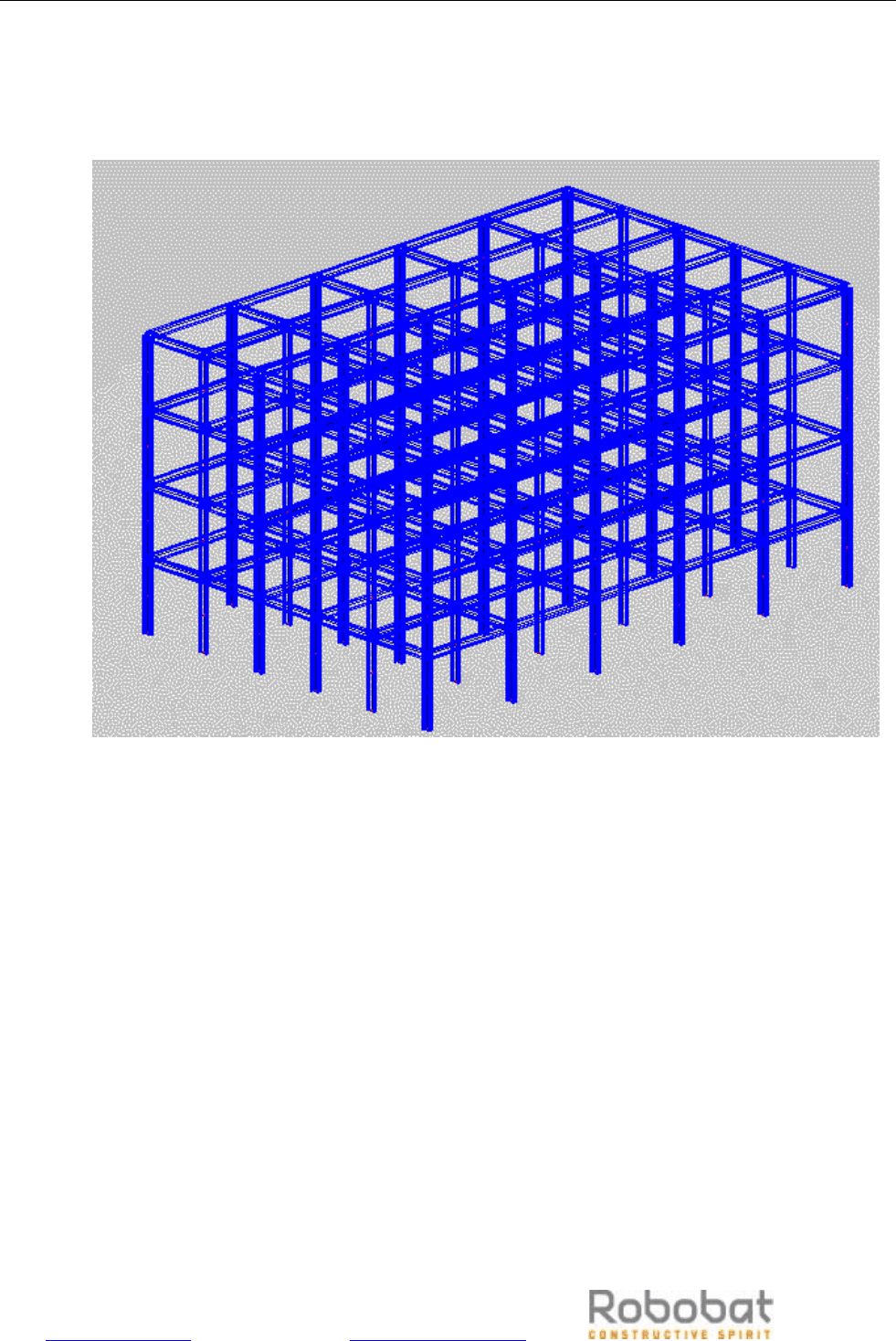
. Расчётная модель

показана на Рис.A2. Имеются 50 собственных, извлечённых по методу BLSI. Выбран Алгоритм

решени , что сходимость, начиная с

38 формы, остаётся такой медленной, что за 20 минут вычислений не получено никаких

результатов. Как только ускорение за счёт сдвига (обновление сдвига принималось после

жет оказаться трудоёмкой процедурой, особенно для круп омасштабны задач. Таким

образом, окончательное решение о применении сдвига должно быть принято на основе опыта и

интуиции пользователя.

ледующий пример иллюстрирует выгоду от применения сдвигаС

я профильный. Принята погрешность 1.0e-09. Оказывается

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 568 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

каждо ии) было активировано, время вычислений

стало идно, можно привести множество примеров, когда

примен число итераций, однако, оно увеличивает время вычислений. Мы

рекоме вать ускорение за счёт сдвига, когда традиционный подход (сдвиги

отклю числу итераций на некоторых стадиях работы BLSI.

го 5-го “неконвертированного” шага итерац

составлять 50 секунд. Очев

ение сдвига сокращает

ндуем активиро

чены) приводит к большому

Рис. A2 Пространственная рамная конструкция

Модифицированный метод Ланцоша

Это - корректировка метода Ланцоша в псевдо-режиме на итерационный алгоритм

решения. Обычный метод Ланцоша требует факторизации матрицы жёсткости (смотри A3).

Когда встречается крупномасштабная задача, факторизация матрицы жёсткости остаётся очень

трудоёмкой. В случае больших задач (более 100 000 уравнений), как правило, не только

факторизация матрицы жёсткости требует огромных вычислительных ус ий, но также и

решен

алгоритм решения AEBEIS (смотри [7,8]) применяется для генерации

векторов Ланцоша. Рекомендуется использовать технику ICCF (неполная факторизация

Холеского словливания [7,8,18-20],

тр ),

ил

ие системы

уравнений корректно факторизованной матрицы является дорогостоящим.

Модифицированный метод Ланцоша основан на итерационном подходе. Он позволяет

избежать хранения, сборки и факторизации крупномасштабной матрицы жёсткости.

Вычисление каждого вектора Ланцоша требуют примерно таких же вычислительных усилий,

что и решение статической задачи с единственной правой частью. Что касается псевдо-режима,

он уменьшает требуемое число

векторов Ланцоша по сравнению с модальным режимом, когда

работает модифицированный метод Ланцоша.

Итерационный

) как для многоуровневого аггрегированного предобу так и

для обычного (не многоуровневого). Он обеспечивает быстрые операции при вычислении

произведения матрицы на вектор и быстрое разрешение

соответствующего

предобусловливания. Следует заметить, что погрешность, принятая для итерационного

алгоритм решение(Настройки Задания | Расчёт Конс укции | Параметры определяет точность

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 569 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

ощь (о параметрах итерационного алгоритм решения для статики и

динамики) для более подробной информации.

Предодусловленный метод сопряжённых градиентов (PCG)

Метод PCG [9-13] рекомендуется для определения небольшого числа собственных мод в

модальном режиме, когда применяется итерационный алгоритм решения. Он может

оказаться очень полезным для назначения ветровой нагрузки или проверки нескольких низких

форм, полученных по методу PCG_Ritz. Доступны все виды предобусловливания, определённые

для статического расчёта (смотри Инструментальные Средства / Настройки Задания /

Итерационный / Параметры). Могут использоваться все

типы матрицы масс

(консистентный, сосредоточенный с вращениями и сосредоточенный без вращений).

Предобусловленный метод сопряжённых градиентов основан на прямой минимизации

показателя Рэлея

вычисления векторов Ланцоша. Обычно достаточно принять 1.0e-04. Чем большее Число Форм

будет принято по внимание, тем ближе нижние вектора Ритца будут к соответствующим

собственным модам, и тем более полные суммы модальных масс будут достигнуты.

Смотри Пом

()

x,x

ρρ

(A11)

осредством градиентного подхода, где: k – число итераций,

соответствующая

аппроксимация собственного значения. Градиентный подход отыскивает такое значение

параметра

, которое обеспечивает минимальное значение

из (A11):

pxx

kkkk 1

∗

(A12)

где

- вектор сопряжённых направлени Поиск подходящего значенияй.

[смотри 9-

13] приводит к:

)

()

()()(

()

adbc

mbnd

ncmaadbcmbnd

−

∆+−

−−−−=∆

x,x

p,p

p,x

p,p

p,x

ρρ

Предобусловливание

B применяется для ускорения сходимости

(A13)

Направление градиента определяется как

111 +++

⇒=

kkk

zrBz

)x,x/()xx(2g

1k1k1k1k11k ++++++

−−=

MKM

(A14)

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 570 -

WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net

Новое направление градиента определяется как

k1k1k

pzp

+−=

(A15)

где

()

1k1

Итерации выполняются до тех пор, пока

tol

kkk

>−=

++++++++ 1k11k1k11k11k

x/xxx/r

MKMM

λλλ

, (A16)

где

tol

- желательный допуск. Обычно tol = 1.0e-02 обеспечивает очень хорошую

точность для инженерных целей. Следует помнить, что показатель сходимости (A16) вычислен

с очень сильной норме (смотри часть, касающуюся точности вычислений). Допуск, упомянутый

выше, обеспечивает точность собственных значений не ниже 1.0e-04.

Когда первая собственная пара сходится, она запоминается, как окончательный

результат, и итерации приступают к вычислению следующей. Для предотвращения

дублирования собственных пар на каждом шаге итерации применяется процедура

ортогонализации ранее определённых собственных векторов. Этот процесс применяется до

тех пор, пока не будут получены все желаемые собственные пары.

Наиболее эффективным способом ускорения сходимости метода PCG является

реализация хорошего предобусловливания. Все виды предобусловливания, представленные для

итерационного алгоритма решения, применимы для метода PCG. Настоятельно рекомендуется

применять многоуровневое Предобусловливание [18-20] или не-многоуровневое

Предобусловливание с ICCF [9-12] сглаживанием от алгоритма решения AEBEIS [7,8].

Подробности смотри в Помощи.

Градиентный метод Ритца (PCG_Ritz)

Метод PCG_Ritz [8] является быстрым методом определения набора векторов Ритца в

псевдо-режиме, когда выбран итерационный алгоритм решения. Такой подход может быть

очень плодотворным для сейсмических расчётов и спектрального анализа конструкций

среднего размера, включающих (10 000 – 60 000) уравнений.

Он основан на генерации ортогональной системы базисных векторов. Градиентный

подход с многоуровневым аггрегированным предобусловливанием на основе методики

элемент

-за-элементом применяется для минимизации показателя Рэлея для каждого шага

подготовки базиса вектора. Это гарантирует эволюцию базисного вектора к самой низкой

собственной моде без аггрегирования и декомпозиции крупномасштабной матрицы жесткости.

Такой метод часто оказывается более эффективным для анализа динамических реакций по

сравнению с классическим методом модальной суперпозиции, в особенности для

анализа

сейсмической реакции. Предложенный метод позволяет применять произвольные типы

конечных элементов благодаря аггрегированному подходу и обеспечивает быстрое решение и

умеренные требования в отношении дисковой памяти, вызванные применением техники

элемент-за-элементом. Этот метод является особенно эффективным, когда используется

консистентная матрица массы.

Данная задача на собственные значения формулируется следующим образом:

−

MK (A17)