Robot Millennium (Версия 20.0). Руководство пользователя
Подождите немного. Документ загружается.


ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 541 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
нтов перемещения:
n
n
δ
+1
Точка входа для элементной процедуры - принцип виртуальных перемещений,
записанный в следующей форме для инкреме
udVeFdVCdV
V
ijij
V
ijklijklijij
δτεδεηδτ
∀∆−=∆∆+∆
∫∫∫
,
где: ∆ε инкремент деформации при переходе от
n
n
B
к
1+n
B
, ∆e, ∆η его составляющие -
соответственно: линейная и нелинейная по отношению к инкременту перемещения ∆u,
принимая во внимание, что τ является напряжением, относящимся к конфигурации сылки, а
Cijkl – это тенз
с
ор тангенциальных модулей упругости.
пция
Нелинейная
т.е. к теории второго порядка. Так как
физиче крементная формулировка, однако, без
модификации геометрии
Loc
},
Принимая во внимание, ч
000010
000000
000
000
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎦
⎤
⎣
⎡
является матрицей отбора.
++
L
e
nn
LLoc
11
ff
KK
σ
ца жёсткости напряжений
n
Loc
n
11
++
= ff
О
Она относится к нелинейной формулировке,
ская нелинейность возможна, вводится ин
элемента.
Кинематические соотношения
Инкременты деформации в матричном представлении:
gHguΒηeE
T
2/1+∆=∆+∆=∆
где:
wvu ;,;,;,;,;,{
φφφ
=g
тогда градиент инкремента перемещения
g = Γ∆u
N
T
xzxyxxxxx
x
,NΓ =
то )3(
000000
000100
);2(;010
DD
N
⎥
⎥
⎢
⎢
⎥
⎥
⎢
⎢
=
H
000000
000000
Вектор усилий в узлах и матрица жёсткости элемента
K
∫
−−=−−
++++
+
+
NL
n
L
n
ext
nn
n
nT
xt
dx
int
1
int
111
1
1
fffuKΣB
σ
=
+=
∫
=
L
T
L
dx
0
DBBK
∫
=
N
T
s
dxN
0
)( ΓHΓK
Алгоритм на уровне элемента
Геометрия элемента не изменяется, локально - глобальное преобразование выполнено с
использованием матрицы начального преобразования
T
0
GloLoc
uTu ∆=∆
0
,
0
2/1 EHgguΒE ∆−+∆=∆
T
Loc
вычисление обобщённых деформаций
)∆=
++
EΣΣΣ ,(
11 nnn
расчёт напряжений (внутренних усилий)
)(
1+
=
n
ΣKK
σσ
матри
NL
n
L
n
t int
1
int
1
++
−− ff
ex
Loc
T
Glo
fTf
0
=

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 542 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
+=
LLoc
пция P-DELTA
Это - определённый
перемещения. Здесь при
ектор усилий в узлах и матрица жёсткости элемента
K
σ
KK
TKTK
00
Loc
T
Glo
=
О
вариант описания стержня, применимый к описанию большие
менён подход обновлённого Лагранжева описания.
В
)3(
000000
000000
000000
0000
0000
000
),2(
000
0
0
)(
0
1
0
int
11111
D
NM
NM
MMN
DNM
MN
dx
dx
dx
z
y
zy
y
y
L
n
T
s
L
T
L
n
ext
nnT
ext
nn
LLoc
O
O
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
=
=
−=−=
+=
∫
∫
∫
+
+++++
ΣΣ
ΓΣΓK
DBBK
ffΣBff
KKK
σ
Алгоритм на уровне элемента
Изменение геометрии элемента,
локально-глобальное преобразование выполнено с
использованием текущих матриц преобразования
,
вычисление обобщённых деформаций
вычисление напряжений (внутренних усилий) в соответствии
с пунктом 3
для текущих напряжений
TT
1
,
+nn
Glo
n
Loc
uTu ∆=∆
0
)( EuΒΒE ∆−∆+=∆
LocNL
)∆=
++
EΣΣΣ ,(
11 nnn
,
NL
n
L
n
ext
n
Loc
n
int
1
int
111 ++++
−−= ffff
Loc
T
Glo
fTf
0
=
σ
KKK +=
LLoc
матрица жёсткости напряжений
модификация геометрии
n
Loc
x
uLL += обновлённая д ина элемента
n
∆
+1
л
γ
β
α
∆∆∆ ,, Эйлеровы углы, опредёленные так же, как и для координат элемента
},,,0,0,0{
wvL
n
∆∆ , 2/)(
11 xx
φ
φ
γ
∆+∆
=
∆
);,,(
γ
β
α
∆
∆∆=∆ TT матрица преобразования для углов
γ
β
α
∆∆
∆
,,
TTT
nn
⋅∆=
+1
1+
=
Как только состояние равновесия достигнуто на данном шаге инкремента, хранимые
LocGlo
fTf
Преобразование к глобальной системе
σ
KKK +=
LLoc
TKTK
11 ++
=
n
Loc
Tn
Glo
Tn
ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 543 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
данные, описывающие геометрию элемента, перезаписываются:
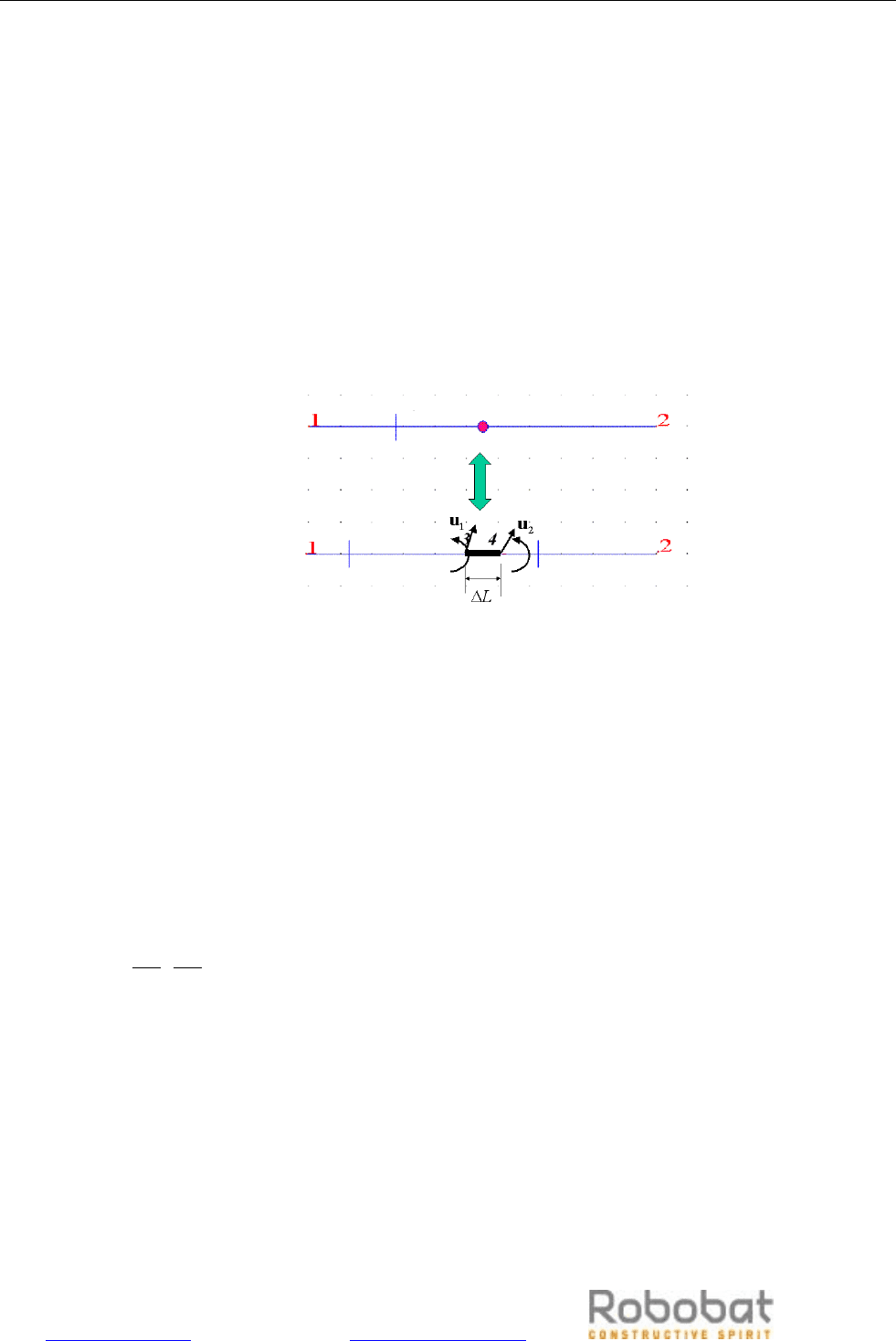
нструкции может быть моделирована
вводом нелинейных ш стики
шарнира, представлен ением
алгори
щённых деформаций Е играют взаимные перемещения узла (относительно локальных
направлений стержня), делённые
на принятую (фиктивную) длину элемента (∆L), которая
равняется минимальной высоте поперечного сечения, и которые выступают в качестве объёма
элемента dV=∆L. Силы и перемещения вновь сгенерированных узлов DSC-элемента составляют
глобальные степени свободы, другими словами, они не подвергаются уплотнению.
LL
nn 1+
=
TT
1+
=
nn
5. Упруго-пластические шарниры
льтернативно, упругопластическая работа коА
арниров в выбранные поперечные сечения стержня. Характери
ного DSC-элементом с 2 вершинами, определены с примен
тма расчёта поперечного сечения, описанного в точке 3, в предположении, что роль
обоб
Алгоритм на уровне элемента
- вычисление обобщённых деформаций в поперечном сечении
- вычисление внутренних усилий (результирующих напряжений) и жёсткости
поперечного сечения в соответствии с пунктом 3.2
л
Glo
u∆=∆ BE
),(
),(
1
1
EΣDD
EΣΣΣ
∆=
∆=
+
+
nn
nn
- вычисление усилий (реакций по концам стержня) и жёсткости DSC-э емента
L
L
nTn
nTn
∆=
∆−=
++
++
BDBK
ΣBf
11
11
где:
)2(;
100
0
0
Dc
sc
⎥
⎥
⎦
⎤
⎢
⎣
⎡
)3(;
33
33
D
x
x
⎥
⎦
⎢
⎣
=
T0
Τ
;,
⎥
⎤
⎢
⎡
−=
TT
B
s
LL
⎤⎡
⎢
−=
⎦⎣
∆∆
0T
Τ

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 544 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
еоретическое Обоснование Динамических Методов, Реализованных в Программе
ROBOT Millennium
МЕТОДЫ ДИНАМИЧЕСКОГО РАСЧЁТА
В ROBOT Millennium
КРАТКОЕ ВВЕДЕНИЕ
В ОСНОВНЫЕ ИДЕИ И АЛГОРИТМЫ
Введение
Этот документ представляет описание методов динамического расчёта, применяемых в
ROBOT Millennium. Подробное теоретическое обоснование и примеры включены в
приложения - чтобы упростить первое чтение. Этот документ не является Руководством для
пользователя и не нацелен на ознакомление пользователя с подробностями интерфейса ROBOT.
Цель текущего документа состоит в том, чтобы истолковать главные идеи, которые
реализованы в этой программе.
Большинство динамических методов в
ROBOT Millennium основано на результатах
расчёта форм колебаний. Необходимо понять, что методы расчёта форм колебаний зависят от
выбранного алгоритма решения. Для профильного алгоритма решения доступны следующие
методы: метод блочной итерации подпространства (BLSI), метод итерации
подпространства(SI)
1
, метод Ланцоша и метод сокращения базиса. Методы, применимые для
разреженного прямого алгоритма решения
2
, включают: метод блочной итерации
подпространства (BLSI), метод Ланцоша и метод сокращения базиса. Для итерационного
алгоритма решения применимы следующие методы: модифицированный метод
(псевд
нтов (PCG).
азреженный прямой алгоритм решения (SPDS) – особый вариант метода исключения
Гаусса Применение этого метода настоятельно рекомендуется для анализа
задач средней и
больш альтернатива
ПРИЛОЖЕНИЕ 3
Т
Ланцоша
о-режим - смотри 3.5 и приложения 3A, 3B), метод градиентов Ритца (PCG_RITZ) и
метод предобусловленных сопряжённых градие
Р
.
ой размерности (10 000 - 200 000 уравнений)
3
Это - хорошая
1
Метод SI был разработан в ROBOT как пер а
к :
Проверка последо ускорение за счёт
Метод неприменим для расчёта форм колебаний с учётом статических усилий.
3
В текущей версии для малых задач, когда все матрицы могут быть размещены в оперативной памяти без
поблочной записи на диск, профильный метод является более быстрым, поскольку обычная процедура умножения
матрицы на вектор работает быстрее, чем поэлементная процедура в методе SPDS. Ситуация
меняется, когда
размерность задачи не позволяет полное размещение всех матриц в оперативной памяти – метод SPDS в этом
случае несравненно быстрее. Этот недостаток метода SPDS будет устранён в следующей версии.
вый метод решения лгебраической проблемы собственных значений.
Такой метод медленный, и поэтому настоятельно рекомендуется применять вместо него метод BLSI или метод
Ланцоша.
2
Временно разреженный прямой алгоритм решения в лючает следующие ограничения
вательности Штурма, опция «Верхние пределы», сдвигов при
работе метода BLSI недоступны для разреженного прямого алгоритма решения. Пропущенные
собственные значения могут частично контролироваться средствами метода BL
SI.

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 545 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
итерационному алгоритму решения.

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 546 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
х подхода. Ан
3.1. Методы расчёта форм колебаний
Расчёт форм колебаний включает два базовы ализ проблемы собственных
значений
0
2
=Φ−Φ
kkk
ρ
ρ
MK
ω
k = 1,2,…,N (3.1)
производится путём определения собственных значений
k
ω
и собственных векторов
k
Φ
ρ
.
Это - первый подход, знакомый инженерам. Второй подход состоит в порождении базисных
векторов
{}
N
qqqQ
ρ
ρ
ρ
,...,,
21
= (3.2)
и поиске аппроксимаций Ритца
k
ω
~
,
k
Φ
ρ
~
(k=1,2,….,N). Он основан на идее, схожей с
методом “Векторов Ритца, зависящих от нагрузки”, предложенным E.L. Wilson [1, 3] и
применённым в SAP2000. Этот подход применяется в сейсмических расчётах, и это - мощный
метод, когда встречаются большие затруднения в получении достаточного процента масс
(смотри раздел 3.5).
В настоящем разделе обсуждаются методы расчёта форм колебаний (первый подход),
которые связаны с
определением собственных значений
k
ω
и собственных векторов
k
Φ
ρ
.
Метод блочной итерации подпространства (BLSI), итерации подпространства,
выборочной ортогонализации Ланцоша и метод сокращения базиса (смотри приложение 3A)
используются, когда выбран прямой алгоритм решения (профильный или SPDS). Метод
итерации подпространства обычно медленный. Поэтому применение метода BLSI или Ланцоша
настоятельно рекомендуется для анализа задач среднего размера и особенно -
крупномасштабных задач, когда требуется большое количество собственных пар.
Метод
сокращения базиса может оказаться очень эффективным для опытного инженера, однако, он
требует дополнительной информации относительно базисных узлов и соответствующих
базисных направлений.
Метод предобусловленных сопряжённых градиентов (PCG) используется в первом
подходе, когда выбран итерационный алгоритм решения. Такой подход может быть очень
эффективен, когда извлечено малое число собственных мод (максимум 5). Он должен
применяться
скорее для расчёта ветровых нагрузок, чем для сейсмического анализа. Метод
PCG м од, когда рассматривается
крупномасштабная задача.
евдо-мода”) представлен в
разделе 3.5.
м методом итерации
подпространства [1-3]. Так же, как
и метод Ланцоша, BLSI может быть применён, чтобы
извлечь большое количество собственных пар (до 100 - 200).
Метод итерации подпространства (SI) может быть использован для анализа матриц
масс всех типов [4] и для анализа отдельных конструкций, однако, в случае большого
количества заданных мод (приблизительно N > 10), этот метод всё еще требует очень больших
затрат времени, особенно для крупномасштабных задач.
Метод Ланцоша [12,16,17] является мощным методом, позволяющим получить большое
количество собственных пар (N ~ 20 – 500 и более). Хотя он является предпочтительным для
крупномасштабных задач, он имеет следующие ограничения:
Невозможно анализировать отдельные конструкции
ожет использоваться для оценки самых низких собственных м
Второй подход (который реализуется в режиме анализа “Пс
Метод блочной итерации подпространства (BLSI) [1,3] является более общим, чем
метод Ланцоша, поскольку он допускает применение матриц масс всех типов (смотри раздел
3.2) и способен анализировать отдельные конструкции. Итерации в блоке постоянного размера
с немедленным исключением сходящихся векторов и добавлением новых начальных обычно
гарантируют более быстрые вычисления по сравнению с обычны

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 547 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
Матрица масс должна быть типа “сосредоточенная с вращениями” или “консистентная”.
Невозможно игнорировать плотность материала (в этом случае достаточно задать
“фиктивную” малую плотность, чтобы избежать этих ограничений).
Метод сокращения базиса [5] известен как улучшение метода Рэлея-Ритца [4], или
метод Бубнова-Галёркина для дискретных систем. Этот алгоритм позволяет получить
приближённые величины первых нескольких собственных пар, если пользователь имеет о них
некоторую информацию. Этот метод требует назначения ведущей степени свободы (MDOF),
чтобы получить упрощённую систему. Таким образом, пользователь может контролировать
процесс создания упрощённой модели.
Это мощный инструмент для пользователей, которые
имеют определённый опыт динамического расчёта конструкций и работают с конструкциями
того типа, поведение которых известно. Этот метод позволяет исключить нежелательные
степени свободы из сокращённой модели и свести исходную сложную задачу с большим
числом степеней свободы к приведенной форме - со значительно меньшим числом степеней
свободы. Опыт
выполнения динамического расчёта конструкций показывает, что пользователь
может столкнуться с определёнными проблемами, когда «методы автоматической редукции»
(имеются в виду BLSI, SI и метод Ланцоша) приводят к очень сложному вычислительному
процессу. Например, формы местных колебаний одиночных стержней могут приводить к
серьёзным проблемам для этих методов, так как процесс вычислений ищет собственные пары
автоматически
, без никакого отбора. Следует отметить, что для большей части случаев в
реальных конструкциях эти местные колебания будут ограничены некоторыми связями,
которые не принимаются во внимание в конечно-элементной модели, или их вклад в общее
движение системы будет несущественным. Обычно процент масс очень мал для таких местных
вибраций. Использование “точных” методов
в этом случае будет приводить к вышеупомянутым
затруднениям, однако, применение приближённого метода сокращения базиса может
значительно упростить процесс вычислений.
градиентов (PCG) [9-13] применим для
итерационного алгоритма решения. Применение такого метода рекомендуется для извлечения
неболь
има (смотри 3.5) с модифицированным методом Ланцоша или метода PCG_Ritz
рекоме
ли ы ан
льного анализа задач средних
размер
факторизации матрицы жёсткости. Вместо этого применяются принципы метода
предоб
.
.2. Типы матрицы масс
К конструкции могут быть применены матрицы масс динамического анализа
“Сосре ений”, «Сосредоточенная с вращениями” и “Консистентная”.
Сосредоточенная без вращений” и “ Сосредоточенная с вращениями ” являются
диагон
возникает, когда пользователь желает рассмотреть
Метод
предопределённых сопряжённых
шого числа собственных пар, когда встречается крупномасштабная задача. Применение
Псевдо-реж
ндован, если требуется определить большое число мод при выполнении сейсмических
расчётов и спектрального анализа, и в бр итерационный алгоритм решения.
Метод
Ritz-gradient (PCG_Ritz) [8] применим для итеративного алгоритма решения в
псевдо-режиме. Он позволяет получить приближённое решение в терминах векторов Ритца. Это
очень быстрый метод для сейсмических расчётов и спектра
ов (10 000 – 100 000 уравнений).
Модифицированный метод Ланцоша является расширением метода Ланцоша, когда
применяется итеративный алгоритм решения. Он работает как обычный метод Ланцоша в
псевдо-режиме, однако, в отличие от метода Ланцоша для прямых алгоритмов решения, он не
требует
условленных градиентов. Такой подход наиболее устойчив среди всех динамических
методов итерационного
алгоритма решения, хотя он часто оказывается не самым быстрым.
Подробные сведения обо всех динамических методах приведены в приложении 3A
3
доточенная без вращ
“
альными матрицами масс. Эти типы матрицы масс требуют минимальных
вычислительных усилий.
Матрица масс “Консистентная”

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 548 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
систем с распределёнными параметрами. Принято считать, что консистентная матрица масс
описыв точенная. Однако, в
большинстве случаев сосредоточенная матрица масс обеспечивает хорошее приближение, так
как очевидно, что инерционные параметры могут быть представлены менее точно, чем
параметры жёсткости. Фактически, кинетическая энергия описывается как перемещения
конструкции, но потенциальная
энергия выражается посредством пространственной
производной перемещений. Известный факт, что ошибка аппроксимации значительно
увеличивается при каждом дифференцировании [4]. Так, для континуальных объектов (твёрдое
тело, оболочки, пластины) возможно аппроксимировать параметры масс менее точно, чем
параметры жёсткости для той же самой сетки. Обычно многочлены Эрмита используются как
функции формы для стержней. Это - точное решение
для большинства статических проблем и
динамических проблем, когда рассматривается сосредоточенная матрица масс. Однако, точные
решения для динамических проблем стержня с распределёнными массами принадлежат к
классу функций Крылова (специальная комбинация гиперболических и тригонометрических
функций). Такой подход позволяет представить параметры жёсткости в таком случае
приближённо, когда Эрмитовы многочлены используются одновременно с консистентной
матрицей
масс. (Позволим себе сделать примечание, что, фактически, это не предназначено для
применения различного типа функций формы для статических и динамических проблем).
Поэтому для большинства случаев это - не большой выигрыш - усложнить динамическую
модель за счёт использования распределённых параметров масс, так как приближённое
решение с консистентными массами получается вместо точного решения для
приближённой
модели (сосредоточенные массы). Более того, обычно собственные массы элементов
стержневых конструкций (балок, колонн и т.п.) являются пренебрежимо малыми в сравнении с
массами стен и крыш (нагрузка от собственного веса), которые учитываются путём
преобразования нагрузки от собственного веса в массы. Такие неконструкционные массы
обычно снижают эффекты масс распределённых элементов.
Всё
приведенное выше приводит к следующему заключению: для большинства
практических случаев сосредоточенная матрица масс обеспечивает достаточно точную
аппроксимацию инерционных свойств конструкции. Следует помнить, что матрица
сосредоточенных масс требует значительных вычислительных усилий, если анализируется
крупномасштабная проблема. Нужно убедиться, что применение консистентной матрицы масс
будет оправдано, перед отбором такого типа матрицы для анализа.
Предполагается, что матрица масс должна быть “Консистентной”, если в расчётной
модели используются жёсткие связи.
Если применяется разреженный прямой или итеративный алгоритм решения, для
вычисления матрично-векторного произведения используется техника элемент-за-элементом
(ЭЗЭ). Это означает, что консистентная матрица масс никогда не сможет быть составлена,
однако, все операции выполняются только на
уровне элемента. Для профильного (skyline)
алгоритма решения консистентная матрица масс составляется и хранится точно в таком виде,
что и матрица жёсткости. Для небольших задач (как максимум ~3000 уравнений) техника
профильного алгоритма является более быстрой, хотя она остаётся очень трудоёмкой, когда
размер задачи увеличивается.
Можно использовать дополнительные сосредоточенные массы (присоединённые массы)
и конвертировать статические
нагрузки в массы.
Когда выбраны метод Ланцоша, PCG_Ritz или модифицированный метод Ланцоша
(итеративный алгоритм решения), доступными являются только “Сосредоточенная с
вращением” и “консистентная” матрицы масс.
3.3. “Верхние пределы ”
Возможно вычислить все собственные значения и собственные моды, которые не
у
ает инерционные свойства конструкции более точно, чем сосредо

ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 549 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
превос ие трактуется как “верхний
предел . Когда “верхний предел” активирован,
ROBOT ищет
,.....,,
ωωωω
≤
, где - это
собственных значений “n”, меньших
“верхн г предела”. На следующем шаге алгоритм генерирует n собственных пар, каждая из
которых
ует
“верхние
р, такая проблема может возникнуть, когда пользователь работает с
Франц
е
ходят определяемого пользователем значения. Это значен
*
”
21
n
“верхний предел”. Алгоритм работает в два шага. На первом шаге выполняется проверка
последовательности Штурма. Она определяет число
*
ω
е о
меньше “верхнего предела”.
Метод Ланцоша и метод BLSI рекомендуются для вида расчёта, который использ
пределы”, так
как обычно требуется получить большое число собственных пар.
Критерий процента участия масс (смотри раздел 3.4) игнорируется, когда активирован
“верхний предел”.
Наприме
узскими сейсмическими Нормами PS-92. Требуется, чтобы были приняты в расчёт все
частоты, меньшие 33 Гц.
3.4. Процент участия масс
Можно задействовать критерий процента участия масс. Процент масс для каждой моды
(k=1,2,…,N) определяется как
()
dir
dir
kdirk
Mm /
2
,
Γ= ,
гд
dir
T
k
dir
I
ρ
ρ
MΦ= ,
dir
k
Γ
являет
k
Γ ся коэффициентом участия масс для k-ой собственной
моды,
dir
I
ρ
- вектор единичной трансляции в направлении (dir = X,Y,Z),
dir
T
dirdir
IIM
ρ
ρ
M= - общая
масса в направлении dir,
T
k
Φ
ρ
- k-я собственная мода, Φ
T
k
1=Φ
k
ρ
ρ
M .
Процент масс для направления dir равняется M%dir
()
dir
N
k
dir
k
M
∑
=
Γ
=
1
2
. Он определяет вклад
всех мод, вовлечённых в движение конструкции в рассматриваемом направлении.
Если выбран режим “Анализ форм колебаний”, и процент масс для указанного
максимального числа узлов меньше требуемого, пользователь получает сообщение о
неудовлетворительном проценте масс, в то время как вычисления продолжаются без каких-
либо поправок..
новить
Пс
автоматический поиск требуемого процента масс. Подробности представлены в разделе 3.5.
. Ре
это ы динамического расчёта
(режимы): Модальный, Сейсмический, Псевдо-мода.
Некоторые сейсмические нормы (UBC-97, Французские нормы PS-92) требуют, чтобы
сумма масс для каждого направления (или только для горизонтальных направлений) была не
меньше 90%.
екоторые “жёсткие” проблемы могут возникнуть, когда очень трудно достигнуть
заданной суммы масс из-за малых вкладов
большого числа самых низких мод. Обычно эта
проблема вызывается локальной особенностью самых низких мод. Сейсмический режим и
Псевдо-мода призваны улучшить ситуацию в таких сложных задачах. Эффективность таких
подходов иллюстрируется приложением 3C. Для этих двух режимов применим метод Ланцоша
для прямых алгоритмов решения. Модифицированный метод Ланцоша и метод PCG_Ritz
применимы для псевдо-режима
, когда выбран итеративный алгоритм решения.
1. Модальный режим
Этот режим составляет хорошо известный подход, реализованный в прежних версиях
ROBOT.
Необходимо уста режим “Сейсмический” или “
евдо-мода”, чтобы обеспечить
3.5 жимы расчёта
м разделе будут представлены следующие способВ
Н
ROBOT MILLENNIUM v 20.0 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ Март 2007 - 550 -
WEB: www.ar-cadia.com.ua Эл.почта: office@robobat.odessa.net
Применимые методы: BLSI, SI, Ланцоша и Метод Сокращения Базиса для прямых
алгоритмов решения и метод PCG для итеративного алгоритма решения.
ритерий сходимости для прямых алгоритмов решения: итерации прекращаются, когда К
to
k
i
k
i
<
−
ωω
/
1
;,...,2,1 Ni = k - номер иl
k
i
−
ω
, где терации, N – число мод (определяется
пользователем). Метод сокращения базиса не производит проверки на сходимость, поскольку
это - не итерационный подход хотя и является разновидностью метода Ритца. Он требует
увеличения числа ведущих степеней свободы для увеличения точности результата.
ритерий сходимости для метода PCG (итеративный алгоритм решения):
,
К
tol
kkkkkkk
<ΦΦ−
ρ
ρ
Φ=Φ
ρ
ρ
MM
λλ
/ где
Подробности описаны в приложении 3A.
Верхние Пределы – значения нижней границы для периода, частоты и пульсации; если
этот параметр отличен от 0, будут рассчитаны все последовательные собственные пары от 0 до
Верхнего Предела.
т масс (сумма масс для всех рассчитанных мод для каждого
направления)
KMr
λ
/, Nk
kk
,...2,1,
2
==
ωλ
Mass% - процен
Проверка Штурма является проверкой пропущенных собственных пар между 0 и
параметром сдвига
σ
и состоит в п диагонали
разложенной смещённой матрицы
1
)(
−
− MK
σ
сделать примечание, что для сейсмического и иза вовсе не обязательно
процент модальной массы для каждого направления. Если такое условие выполнено, полнота
базиса обеспечена. Имейте в виду, что реализация метода
одсчёте отрицательных элементов на
Это очень дорогостоящая процедура для крупномасштабных задач. Позволим себе
спектрального анал
получить непрерывные спектры собственных значений. Важно только обеспечить достаточный
BLSI позволяет выполнить
частичную верификацию спектров собственных значений без проверки Штурма – смотри
описание метода BLSI.
Ч
исло
Мод
В
ерхние
предел
ы
%
масс
Поведение Программы
N 0
(
Неактив
но)
0
(
Неактив
но)
Проверка Штурма задействована. Такая
опция гарантирует, что пропущенные частоты для
первых N мод отсутствуют. Она доступна для
прямых решателей, когда применяются методы
BLSI, SI или Ланцоша. Он недоступна для метода
сокращения базиса и для всех итерационных
методов решения. Определяет N первых
последовательных собственных мод. Выполняется
проверка Штурма. Если обнаружены пропущенные
частоты, пользователь получает предупреждение о
количестве пропущенных
частот. Если пользователь
отвечает:
Да, тогда итерационный процесс
продолжается, в течение которого определяется
число пропущенных собственных пар. После этого
выполняется повторная проверка Штурма.
