Рашников В.Ф, Салганник В.М., Шемшурова Н.Г. Квалиметрия и управление качеством продукции
Подождите немного. Документ загружается.

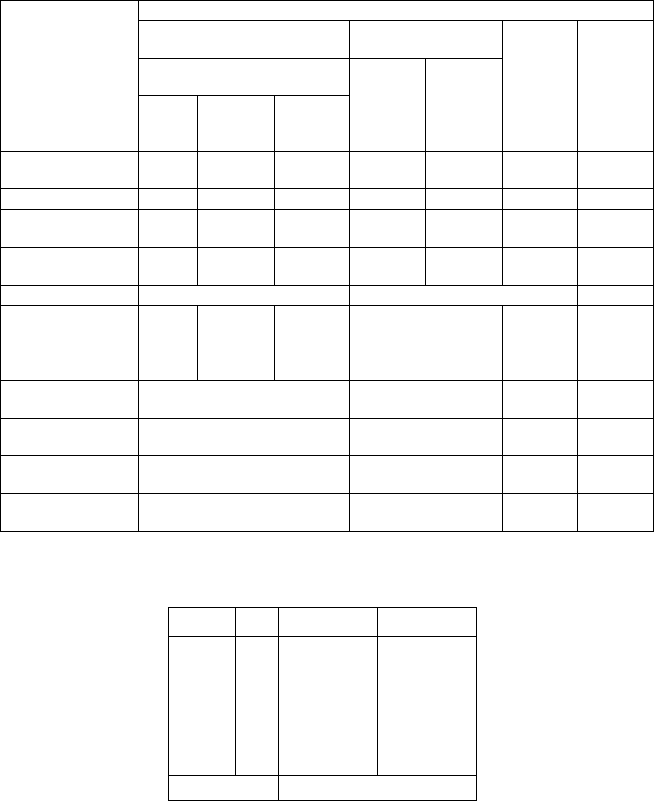
61
Таблица 10
Выписка из стандартов
"Швеллеры гнутые неравнополочные. Сортамент"
Параметр не-
равнополоч-ного
гнутого швелле-
ра 67х65х35х3
мм
(длина 9 м)
Предельные отклонения
Россия - ГОСТ 8281-80
Болгария –
БДС 13403-76
Чехия –
CSN
426973
jk 154
Япония
JIS G
3350
(1977)
Точность профилирова-
ния
Поштуч-
ное
профи-
лирова-
ние
Непрер.
профи-
лирова-
ние
высо-
кая
повы-
шенная
обычная
Стенка 67мм +0,5
-1,0
±1,5 ±2,0 ±1,5 ±1,3 ±1,0 ±1,5
Полка 35 мм
±
0,5
±
1,0
±
1,5
±
1,5
±
1,0
±
0,5
±
1,5
Полка 65 мм +0,5
-1,0
±1,5 ±2,5 ±2,0 ±1,5 ±1,0 ±1,5
Длина профиля
9000 мм
+50 +50 +50 +50 +50 +50 +50
Толщина 3 мм
±
0,21
Нет сведений
±
0,28
Предельные
отклонения от
углов, не более,
град.
±1,0
±1,5
±1,5
±1,5
k2
±1,5
Волнистость,
мм / 1 м
<2,0 <2,0 2,0 -
Кривизна, %
от длины
<0,1 <2,5 мм / м - <0,2 %
Скручивание,
град. / м
1,0 (<10 град.) 1,0 (<10 град.) 2,0 -
Радиус подгиб-
ки, R
в
, мм
≤5,0
Таблица 11
К расчету
х
и
σ
х
i
n
|х
-
х
i
|
(х
-
х
i
)
2
65,5
66,0
66,5
67,0
67,5
68,0
2
3
8
6
4
2
1,26
0,76
0,26
0,24
0,74
1,24
1,5876
0,5776
0,0676
0,0576
0,5476
1,5376
Σn = 25 Σ = 4,3856

62
( )
( )
∑
−
−
=
∑
=
1n/
x
i
x
2
σ
/n;
x
i
x
,
где
х
i
- замеренные значения параметра (случайная величина);
n
- объем выборки.
х
= (65,5x2+66x3+66,5x8+67x6+67,5x4+68x2) / 25 = 66,76 мм;
4275,01827,024/3856,4 ===
σ
мм.
*)
**)
*) - допуск по ГОСТ 8281-80 по стенке швеллера h
для профилей нормальной точности;
**) - то же для профилей повышенной точности;
***) - то же для профилей высокой точности;
67 – номинальное значение, которое принимаем за базовое.
Рис. 10. Гистограмма фактических значений замеров по
стенке швеллера
Доверительный интервал фактических значений с надежно-
стью Р=0,99 определяем с помощью правила трех сигм: отклоне-
0
2
4
6
8
10
65,5 66 66,5 67 67,5 68
Значения замеров по высоте стенки
швеллера
Частота
69
***)

63
ние истинного значения измеряемой величины от среднего ариф-
метического значения результатов измерений не превосходит ут-
роенной средней квадратической ошибки этого среднего значения
х
факт
=
х
± 3
σ
= 66,76 ± 0,4275 ⋅ 3 = (65,48...68,04) мм
или
х
факт
=
67
04,1
52,1
+
−
мм.
То есть доверительный интервал по стенке h швеллера
∆
h
= 2,56 мм, а Р
i
пр
=Р
i
номин
±
∆
Р
max
= 67 – 1,52 = 65,48 мм ≈ 65,5 мм.
Можно определить долю продукции в партии, выходящей за
пределы ГОСТ для швеллеров, например, повышенной точности
по выборке из 25 измерений по функции Лапласа [25, табл. 1 и 2
Прил.] или [26, с 356, таблица значений функции Ф(х)]: вероят-
ность выхода значений величины h за пределы ГОСТ 8281-80 в
партии продукции
Р
бр
= 1 - {
Ф
1
[(
х
в
-
х
) /
σ
] +
Ф
2
[(
х
-
x
н
) /
σ
]},
где
х
в
, x
н
–
соответственно наибольшее и наименьшее значения
параметров швеллера по ГОСТ 8281-80 для профилей повышен-
ной точности.
Ф
1
[(
х
в
-
х
) /
σ
] = (68,5 - 66,76) / 0,4275 = 4,07 0,5;
Ф
2
[(
х
-
x
н
) /
σ
] = (66,76- 65,5) / 0,4275 = 2,95 0,4984.
Р
бр
= 1 - (0,5 + 0,4984) = 0,0016 = 0,16% продукции в партии
может выйти за пределы допусков для профилей повышенной
точности - это хороший результат.
Может быть совсем иной результат - о т с т у п л е н и е :
Пример. Дать заключение о качестве партии продукции по
выборке из 10 штук (N = 10), если требования по нормативной до-
кументации следующие: 160 ≤
х
i
≤ 240 условных единиц.
Замеренные значения (
х
i
):
160; 161; 162; 162; 170; 177; 180; 215; 220; 238.
Все замеренные значения (n =10) укладываются в установ-
ленные нормы.
Обычно при выборочном контроле без применения стати-
стических методов такая партия продукции принимается.
При статистическом методе контроля определяем среднее
арифметическое значение замеренных параметров
х
и средне-
квадратическое отклонение
σ
:
х
= 185,5;
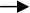
64
σ
=√(650,25+600,25+552,25+552,25+240,25+72,25+30,25+870,25+
¬ ¬
+1190,25+2756,25) / 9 = √ 7514,25 / 3 = 86,68 / 3 = 28,89.
Интервал рассеяния случайной величины (доверительный
интервал) содержит шестикратное среднее квадратическое откло-
нение: (
х
± 3
σ
) = 185,5 ± 86,7 = (98,8...272,2) - что не удовлетво-
ряет требованиям НТД.
Определим вероятность появления брака Р
бр
в партии:
Р
бр
= 1 - {
Ф
1
[(
х
в
-
х
) /
σ
] +
Ф
2
[(
х
-
x
н
) /
σ
]} =
= 1 - {Ф
1
[(240-185,5)/28,89] + Ф
2
[(185,5-160)/8,89]} =
= 1 - [Ф
1
(1,89) + Ф
2
(0,88)] = 1 - (0,47 + 0,31) = 0,22 = 22%
- то есть почти четверть партии продукции не отвечает тре-
бованиям НТД.
Возвращаемся к нашей задаче. Аналогично находим дове-
рительные интервалы фактических значений по остальным гео-
метрическим параметрам и записываем их в таблицу 15.
Определяем весомости показателей качества.
Весомость показателей качества определяем экспертным
методом. Пусть пять независимых экспертов оценивают степень
важности показателей качества по пятибалльной шкале. Исходные
данные заносим в таблицу 12.
Дальнейшую обработку данных ведем по формулам (7) и (8).
Весомость
j
-го показателя у
е
-го эксперта для первого зна-
чения: 4 / 43 = 0,093;
весомость единичного j-го показателя для первого значения:
0,548 / 5 = 0,1096.
Проводим пересчет весомостей с учетом, что
.1
M
K
1;
M
D
i
=
∑
=
∑
γ
ΣМ
1-9
D
= 1 - 0,0716 = 0,9284 - принимаем за единицу, тогда
для первого доминирующего показателя справедлива пропорция
0,1096 - х
0,9284 - 1 х = 0,1181.
Результаты расчетов заносим в таблицу 13.
Определяем степень согласованности назначенных экспер-
тами индивидуальных коэффициентов весомости. Результаты
расчетов заносим в табл. 14.
65
Таблица 12
Исходные данные по степени важности
единичных показателей
№ по-
каза-
теля
j=1,2..n
Показатель (от-
клонения от
размеров)
Весомость (
степень важности
)
D/К
∑
=
m
e
R
e
1
№эксперта (е=1,2,…,n
)
1 2 3 4 5
1
Высота стенки,h
4D 4D 5D 5D 5D D
R
j1
=23
2
Ширина м.п., b
1
5D 5D 5D 5D 5D D
R
j2
=25
3
Ширина б.п., b
2
4D 5D 5D 5D 4D D
R
j3
=23
4
Толщина, S
2D 3D 2D 3D 2D D
R
j4
=12
5
Угол подгибки,
α
5D 4D 4D 5D 5D D
R
j5
=23
6
Длина профиля,l
5D 5K 5D 5D 4D D
R
j6
=24
7
Скручивание
5D 5D 5D 4D 5D D
R
j7
=24
8
Кривизна
5D 4D 3K 4K 5D D
R
j8
=21
9
Волнистость
5D 4D 3K 4K 4D D
R
j9
=20
10
Радиус подг., R
в
3K 2K 4D 3K 3K K
R
j10
=15
∑
=
n
j
R
j
1
43
41
41
43
42
210
1 1
=
∑
=
∑
=
m
e
n
j
R
je
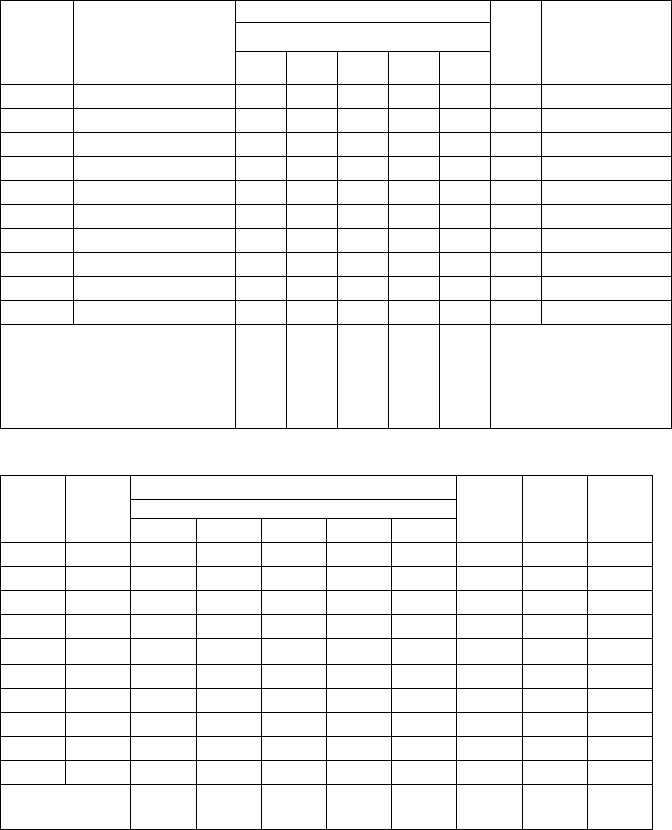
Таблица 13
Определение весомости единичных показателей
j =
=1,..,n
Пока-
за-
тель
M
je
ΣM
je
M
j
M
j
п
e= 1,…, m
1 2 3 4 5
1
h
0,093
0,090
0,182
0,116
0,119
0,548
0,1096
0,1181
2
b
1
0,116
0,122
0,122
0,116
0,119
0,595
0,1190
0,1282
3
b
2
0,093
0,122
0,122
0,116
0,095
0,548
0,1096
0,1181
4
S
0,047
0,073
0,049
0,070
0,048
0,287
0,0574
0,0618
5
α
0,116
0,098
0,098
0,116
0,119
0,547
0,1094
0,1178
6
l
0,116
0,122
0,122
0,116
0,095
0,571
0,1142
0,1230
7 Скр.
0,116
0,122
0,122
0,093
0,119
0,572
0,1144
0,1232
8 Кр.
0,116
0,098
0,073
0,093
0,119
0,499
0,0998
0,1075
9 Волн.
0,116
0,098
0,073
0,093
0,095
0,475
0,0950
0,1023
10
R
в
0,070
0,049
0,098
0,070
0,071
0,358
0,0716
(K) 1,0
=1 =1 =1 =1 =1
ΣΣ=5
ΣM
j
=1
ΣD=1
ΣК=1
66
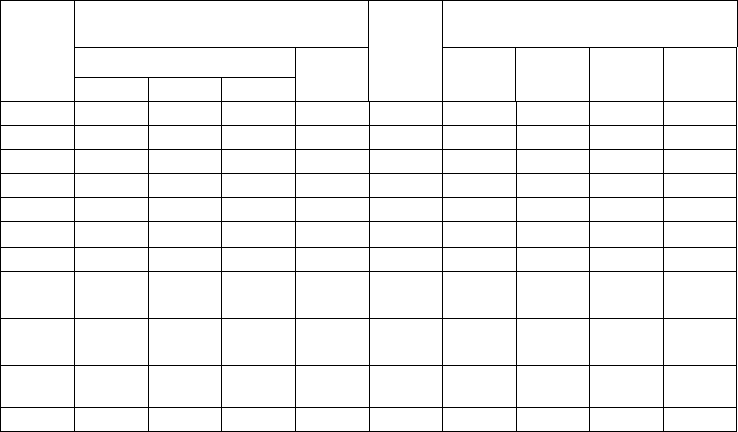
Таблица 14
Определение степени согласованности мнений экспертов
k
v
№
Пока
за-
тель
М
j
ср
(М
j
ср
-М
jе
)
2
Σ
(М
j
с
р
-
-М
jе
)
2
S
j
k
v
1 2 3 4 5
1
h
0,1096
0,00027556 0,00013456 0,00015376 0,00004096 0,00008836 0,00069296
0,013162 0,12
2
b
1
0,1190
0,00000900 0,00000900 0,00000900 0,00000900 0 0,00003600
0,003000 0,03
3
b
2
0,1096
0,00027556 0,00015376 0,00015376 0,00004096 0,00021316 0,00083696
0,014500 0,13
4
S
0,0574
0,00010816 0,00024336 0,00007056 0,00015876 0,00008836 0,00066896
0,0129321
0,23
5
α
0,1094
0,00004356 0,00012996 0,00012996 0,00004356 0,00009216 0,00043890
0,0104749
0,10
6
l
0,1142
0,00000324 0,00006084 0,00006084 0,00000324 0,00036864 0,00055504
0,0117796
0,10
7 Скр.
0,1144
0,00000256 0,00005776 0,00005776 0,00045796 0,00002116 0,00059736
0,012200 0,11
8 Кр. 0,0998
0,00026244 0,00000324 0,00071824 0,00004624 0,00036864 0,00139864
0,0186991
0,19
9
Волн
0,0950
0,00044100 0,00000900 0,00048400 0,00000400 0 0,00094400
0,0153622
0,16
10
R
в
0,0716
0,00000256 0,00051076 0,00069696 0,00000026 0,00000036 0,00121326
0,0174159
0,24
67
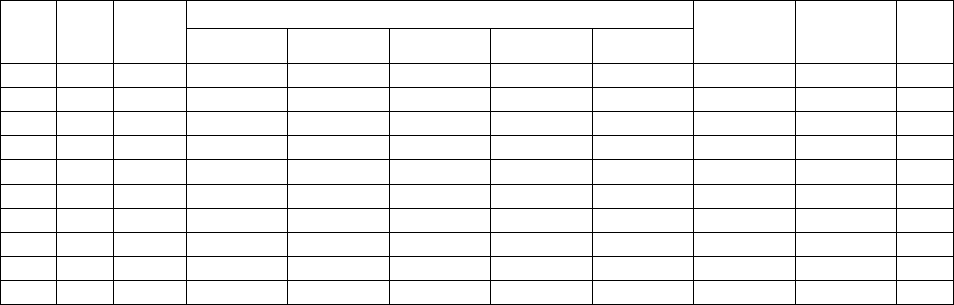
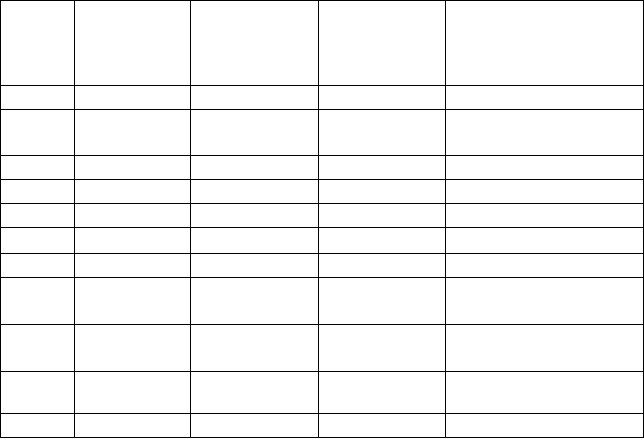
Таблица 15
Оценка относительных показателей качества неравнополочного
гнутого швеллера 67х65х35х3,0 мм по формуле (1)
Пока-
затель
Допустимый интервал значений
Р
i
пр
по
Дове-
рит.инт
P
i
факт
Оценка единичных
показателей, q
i
Г О С Т 8 2 8 1 - 8 0
JIS
Япония
обычн
повыш
высок
Япония
обычн
повыш
высок
1 2 3 4 6 7 8 9 10
h, мм
4,0 3,0 1,5 3,0 2,56 1,56 1,17 0,59 1,17
b
1,
мм
3,0 2,0 1,0 3,0 2,90 1,03 0,69 0,34 1,03
b
2
, мм
5,0 3,0 1,5 3,0 3,20 1,56 0,94 0,47 0,94
S, мм
0,42 0,42 0,42 0,56 0,40 1,05 1,05 1,05 1,40
α, град
3,0 3,0 2,0 3,0 2,5 1,20 1,20 0,80 1,20
l, мм
50 50 50 50 30 1,67 1,67 1,67 1,67
Скруч,
град/м
1,0 1,0 1,0 0,98 1,02 1,02 1,02
Крив.,
% / м
0,1 0,1 0,1 0,2 0,09 1,11 1,11 1,11 2,22
Волн.,
мм / м
2,0 2,0 2,0
1,8 1,11 1,11 1,11
R
в
, мм
5,0 5,0 5,0 3,5 1,43 1,43 1,43
69
Для первого значения
k
v1
= 0,013162 / 0,1096 = 0,12.
Все коэффициенты вариации имеют достаточную согласо-
ванность.
Далее определяем относительные показатели качества
по формуле (1) (табл. 15) и оценки единичных показателей ка-
чества неравнополочного гнутого швеллера по формуле (5)
(табл. 16).
За базовые значения показателей Р
i
баз
при определении
относительных показателей качества можно принять допус-
тимый интервал значений по нормативно-технической документа-
ции (графы 2-5 табл. 15). Так, для стенки швеллера допустимый
интервал по ГОСТ 8281-80 для профилей обычной точности Р
i
баз
=4,0 мм (см. табл. 10); повышенной точности - Р
i
баз
= 3,0 мм; высо-
кой точности - Р
i
баз
=1,5 мм.
Чем меньше доверительный интервал Р
i
факт
, тем выше оцен-
ка, поэтому при определении относительных единичных показате-
лей качества пользуемся формулой q = Р
i
баз
/ Р
i
факт
. Тогда для
стенки швеллера (профили обычной точности) q=4,0/2,56=1,56
(табл. 15, графа 7). Аналогично определяем значения q остальных
единичных показателей профилей относительно базовых значений
обычной, повышенной и высокой точности по ГОСТ 8281-80 (Рос-
сия), и относительно JIS G 3350 - 77 (Япония). Результаты заносим
соответственно в графы 7 – 10 табл. 15.
При определении оценки единичных показателей по
формуле (5) в качестве базового значения единичных показателей
принимают номинальные значения этих показателей (графа 2
табл. 16), что более корректно, чем доверительный интервал. То-
гда предельные значения показателей определяются по формуле
Р
i
пр
=Р
i
номин
±
∆
Р
max
. (
∆
Р
max
– это наибольшее из фактических зна-
чений, составляющих доверительный интервал). Для стенки
швеллера Р
i
пр
= 67 – 1,52 = 65,48 мм ≈ 65,5 мм. Аналогично следу-
ет определять предельные значения остальных показателей. Ре-
зультаты заносим в графу 3 табл. 16. А фактическое значение по-
казателя равно математическому ожиданию: P
i
факт
=
х (см. ранее).
Для стенки швеллера P
i
факт
= 66,76 мм ≈ 66,8 мм. Аналогично оп-
ределяем фактические значения остальных показателей и зано-
сим их в табл. 16.
70
Таблица 16
Оценка единичных показателей качества неравнополочного гнуто-
го швеллера 67х65х35х3,0 мм по формуле (5)
Пока-
затель
Базовое
значение
показателя
Р
i
баз
Предельное
значение
показателя
Р
i
пр
Фактическое
значение
показателя
P
i
факт
Оценка единичных
показателей
1 2 3 4 5
h, мм
67,0 65,5 66,76
1-[(67-66,76)/(67-
65,5)]
2
=0,9822
b
1,
мм
35,0 36,4 36,1 0,38
b
2
, мм
65,0 63,9 64,7 0,93
S, мм
3,0 2,85 2,95 0,89
α, град
90,0 90,5 89,8 0,84
l, м
9,0 9,03 9,02 0,56
Скруч,
град/м
0 0,98 0,95 0,06
Крив.,
% / м
0 0,09 0,055 0,63
Волн.,
мм / м
0 1,8 0,9 0,75
R
в
, мм
3,0 3,5 3,2 0,84
Далее определяем уровень качества профиля по отношению
к требованиям стандартов по формуле:
n
К
у
=
Σ
(q
j
х M
j
).
j=1
Тогда по отношению к требованиям российского стандарта
уровень качества неравнополочного гнутого швеллера производ-
ства ЗАО "Прокат - Гнутый профиль" для профилей обычной, по-
вышенной и высокой точности соответственно равен:
К
у
обычн
= 1,56 x 0,1096 + 1,03 x 0,1190 + 1,56 x 0,1096 + 1,05x
x 0,0574 + 1,2 x 0,1094 + 1,67 x 0,1142 +1,02 x 0,1144 + 1,11 x
x 0,0998 + 1,11 x 0,095 + 1,43 x 0,0716= 1,28;
К
у
повыш
= 1,13;
К
у
высок
= 0,93.
