Рабинович С.Г. Погрешности измерений
Подождите немного. Документ загружается.


где
q
t
— q-процентная точка распределения Стьюдента; значение
q
t
находят
в табл. П-7 по числу степеней свободы k = п—1 и уровню значимости
α
−
=
1q .
Приведенные выше методы позволяют проверить допустимость гипотезы о
нормальном распределении наблюдений и, следовательно, о допустимости
применения распределений Стьюдента. Уровень значимости q, принимаемый для
построения доверительного интервала, следовало бы согласовывать с уровнем
значимости, принятым при проверке нормальности распределения, но эта
задача не имеет пока что определенного решения.
Доверительная вероятность не должна быть слишком низкой. В
измерительной технике постепенно все чаще доверительную вероятность
принимают равной 0,95 или 0,99 и лишь иногда 0,90. Эти цифры соответствуют
соображениям, изложенным в § 1-6.
На практике доверительные интервалы строят на основе распределения
Стьюдента, часто без проверки допустимости этого. То, что при этом, как
правило, не возникает недоразумений, косвенно подтверждает высказанное
выше мнение, что реальные распределения — это усеченные распределения,
более «узкие», чем нормальные.
Если измерение выполняется изученным методом и известно среднее
квадратическое отклонение наблюдений для этого метода
σ
, то доверительный
интервал для А строят по нормальному распределению:
α
σ
α
=
≤−
n
zAxP
2
(3-25)
где
α
— выбранная доверительная вероятность, п — число выполненных
наблюдений,
2
α
z
— квантиль нормированного распределения Лапласа,
которую находят по табл. П-2 для вероятности, равной
2α
.
Иногда строят доверительные интервалы для среднего квадратического
отклонения. Для этого используют распределение
2
χ
, приведенное в табл. П-3.
Доверительный интервал с границами
σ
χ
~
1
H
n −
и
σ
χ
~
1
B
n −
для вероятности
ασ
χ
σσ
χ
=
−
<<
−
~
1
~
1
BH
nn
P
(3-26)
находят следующим образом. В табл. П-3 даны вероятности
{
}
22
q
P χχ > . Значение
2
B
χ
находят из таблицы для
2
1
α
ρ
+
=
B
,
а
2
H
χ
— для
2
1
α
ρ
−
=
H
.

Например, получено
5
102,1
~
−
⋅=σ
,
10
=
n
. Примем
90,0
=
α
. Тогда
95,0
2
9,01
=
+
=
B
ρ , 05,0
2
9,01
=
−
=
H
ρ . Число степеней

свободы k = 10-1=9. По табл. П-3 находим
25,3
2
=
B
χ
и
92,16
2
=
H
χ
.
Доверительный интервал будет
⋅⋅
−
⋅⋅
−
−− 55
202,1
325,3
110
;202,1
92,16
110
,
т. е.
[
]
55
0,10,2;1088,0
−−
⋅⋅
.
Доверительная вероятность в этом случае может быть принята
меньшей, чем при построении доверительного интервала для истинного
значения измеряемой величины. Часто можно считать достаточным
70,0
=
α
.
3-8. Толерантные интервалы
Толерантным интервалом называется интервал, который с заданной
вероятностью
α
содержит не менее чем заданную часть р
0
всей
совокупности случайной величины (генеральной совокупности). Таким
образом, толерантный интервал — интервал для случайной величины, и
этим он в принципе отличается от доверительного интервала, который
строится, чтобы накрыть неслучайную величину.
Границы толерантного интервала
σ
~
1
Kxl −=
и
σ
~
2
Kxl +=
,
где
x
и
σ
~
вычисляются по формулам (3-11) и (3-18) на основе
имеющейся группы данных.
Толерантный множитель вычисляется по формуле
+
++=
∞
n
z
n
z
zK
12
105
2
1
2
αα
,
где
∞
z
и
α
z
определяются по уравнениям [49]:
0
2/
)(2
2
1
2
ρ
π
==
∫
∞
∞
−
∞
−
z
z
zФdye
y
,
α
π
α
α
−=−=
∫
∞
−
1)(5,0
2
1
2/
2
z
zФdye
y
Значения
)(zФ
приведены в табл. П-2.
Для наиболее употребительных уровней
α
и
0
ρ
составлены таблицы
для определения толерантного множителя.
Если, например, измерена чувствительность группы тензорезисторов,
то полученным данным можно найти интервал с границами
21
,ll
, в
котором с заданной вероятностью
α
будет находиться чувствительность
не менее части
0
ρ
всей партии (или всей совокупности) тензорезисторов
данного типа.

Термин «толерантный интервал» часто интерпретируют как допусковый интервал, а
«толерантные границы» — как границы поля допуска, допуск. Однако в такой трактовке этих
терминов есть существенная неточность.
Допуск, или границы поля допуска, устанавливают, как правило, до изготовления изделия и
так, что изделия, интересующий нас параметр которых выходит за пределы поля допуска,
признаются негодными, бракуются. Иными словами, границы поля допуска — жесткие границы, не
связанные ни с какими вероятностными соотношениями.
Толерантный же интервал определяют на основе исследований уже изготовленных изделий и
вычисляют его границы так, чтобы с заданной вероятностью в этот интервал попадали параметры
заданной доли всего возможного числа изделий. Таким образом, границы толерантного интервала, так
же как и границы доверительного интервала, — случайные величины, и этим они отличаются от
допусковых границ, или допусков, которые являются неслучайными.
3-9. Проверка однородности наблюдений
Измерения с большими случайными погрешностями требуют
настороженного внимания. Необходимо удостовериться в том, что
получаемые результаты, статистически подконтрольны, устойчивы, т. е.
что результаты наблюдений группируются вокруг одного и того же центра
и имеют одну и ту же дисперсию. Если метод измерения и объект
исследования изучены мало, то наблюдения при таком измерении нужно
повторять до тех пор, пока не появится уверенность в устойчивом
характере этих результатов [64]. Тем самым определяются
продолжительность исследования и необходимое число наблюдений.
Устойчивость измерений часто оценивается интуитивно на основе
длительных наблюдений. Однако известны математические методы,
полезные для решения рассматриваемой задачи, так называемые методы
проверки однородности. Применительно к измерениям рассматривается
однородность групп наблюдений. Необходимые признаки однородности
групп наблюдений состоят в том, что оценки средних арифметических и
дисперсий не должны иметь значимых смещений относительно друг друга.
Выполнение необходимых признаков однородности — условие
необходимое, но недостаточное для действительной однородности, так как
группы наблюдений можно неправильно или неудачно выбрать.
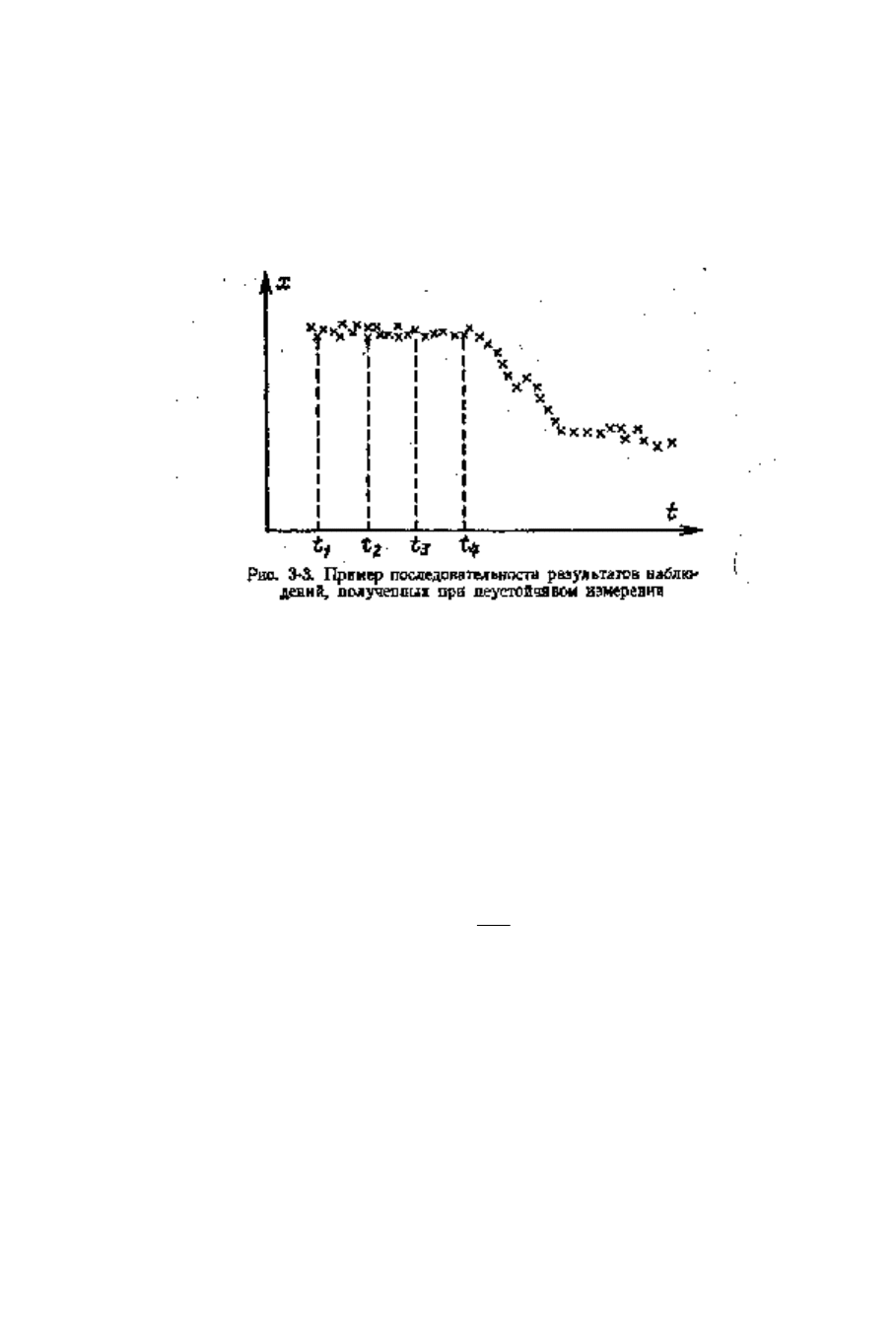
На рис. 3-3 приведены результаты наблюдений некоторой величины,
представленные в той последовательности, в какой они были получены.
Если взять три группы наблюдений, выполненные за интервалы времени
342312
,, tttttt −−−
, то они, по-видимому, будут однородными. Между тем
последующие наблюдения дали бы существенное отличие от первых, и в
целом полученные по первым группам наблюдений результаты дадут
картину устойчивого, статистически подконтрольного измерения, чего нет
на самом деле.
Выбор групп для контроля однородности остается задачей
специалиста-экспериментатора, так же как и отграничение одной группы
от другой. Обычно наблюдения, выполненные через
интервалы времени, большие, чем время для получения какой-то совокупности
результатов наблюдений, относят к разным группам. Целесообразно иметь в
группе порядка 10 наблюдений (от 5 до 10 наблюдений согласно работе [20,
стр. 123] и лучше — несколько таких групп, чем одну группу с большим числом
наблюдений.
Приведем некоторые из числа наиболее часто применяемых методов
проверки допустимости различия между оценками дисперсий и различия между
средними арифметическими групп наблюдений. Предполагается, что
распределения наблюдений предварительно проверены на нормальность.
Проверка допустимости различия между оценками дисперсий
выполняется с помощью критерия Р. Фишера в случае двух групп наблюдений и
критерия М. Бартлетта, если групп больше. Приведем последовательно оба
метода.
Пусть несмещенные оценки дисперсий этих групп
2
1
S
и
2
2
S
, причем
2
2
2
1
SS >
. Число наблюдений в группах
1
n
и
2
n
, так что степени свободы
равны соответственно
1
11
−= nk
и
1
22
−= nk
. Составляем отношение
2
2
2
1
S
S
F =
(3-27)
Затем из табл. П-8 и П-9, где приведены вероятности
{
}
qFFP
q
=>
(3-28)
для различных степеней свободы
1
k
и
2
k
, выбираем значение
q
F
.
Гипотеза принимается, т. е. оценки дисперсий можно считать
отвечающими одной и той же дисперсии, если выполняется неравенство
q
FF <
. Уровень значимости при этом равен 2q. Теперь пусть у нас есть L
групп и для них найдены
2
2
2
1
,...,SS
— несмещенные оценки дисперсий групп
наблюдений (L>2),

каждая из которых имеет
1−=
ii
nk
степеней свободы, причем все
3
>
i
k
.
Проверка гипотезы о равенстве дисперсий групп основана на статистике
∑∑
==
−
=
L
i
ii
L
i
ii
SkSk
N
NM
1
2
1
2
ln
1
ln
(3-29)
где
∑
=
=
N
i
i
kN
1
.
Если гипотеза о равенстве дисперсий верна, то отношение
−
−
+
=
∑
=
L
i
i
NkL
M
1
2
1
11
)1(2
1
1
χ
(3-30)
распределено приближенно как
2
χ
с
1
−
L
степенями свободы [6].
Задаваясь уровнем значимости q, из табл. П-3 находим
2
q
χ
такое, что
{
}
qP
q
=>
22
χχ
. Если выполняется неравенство
22
1 q
χχ <
, то различия между
оценками дисперсий допустимы.
Проверка допустимости различий между средними арифметическими
выполняется тоже по-разному в случав двух групп наблюдений и если этих
групп больше.
Рассмотрим сначала сравнение средних арифметических для двух групп
наблюдений, когда наблюдений много, так что каждую из оценок дисперсий
можно считать совпадающей со своей дисперсией.
Обозначим через
1
x
,
2
1
σ
,
1
n
данные, относящиеся к одной группе, а через
2
x
,
2
2
σ
,
2
n
— ко второй. Составим разность
21
xx −
и оценим ее дисперсию:
( )
2
2
2
1
2
1
21
2
nn
xx
σσ
σ +=−
.
Затем, выбрав определенный уровень значимости q, находим
q
−
=
1
α
и
по табл. П-2 — аргумент
2α
z
функции Лапласа, соответствующий
вероятности
2α
.
Различие между средними арифметическими считается допустимым, если
(
)
21
2
21
xxzxx −≤− σ
α
(3-31)
.
Если дисперсии групп неизвестны, то задача решается лишь при
условии, что обе группы имеют одинаковые дисперсии (оценки этой дисперсии
2
1
~
σ
и
2
2
~
σ
могут, естественно, отличаться). В этом случае вычисляется
( ) ( )
(
)
21
2121
2
22
2
11
21
2
~
1
~
1
nn
nnnn
nn
xx
t
+
−+
−+−
−
=
σσ
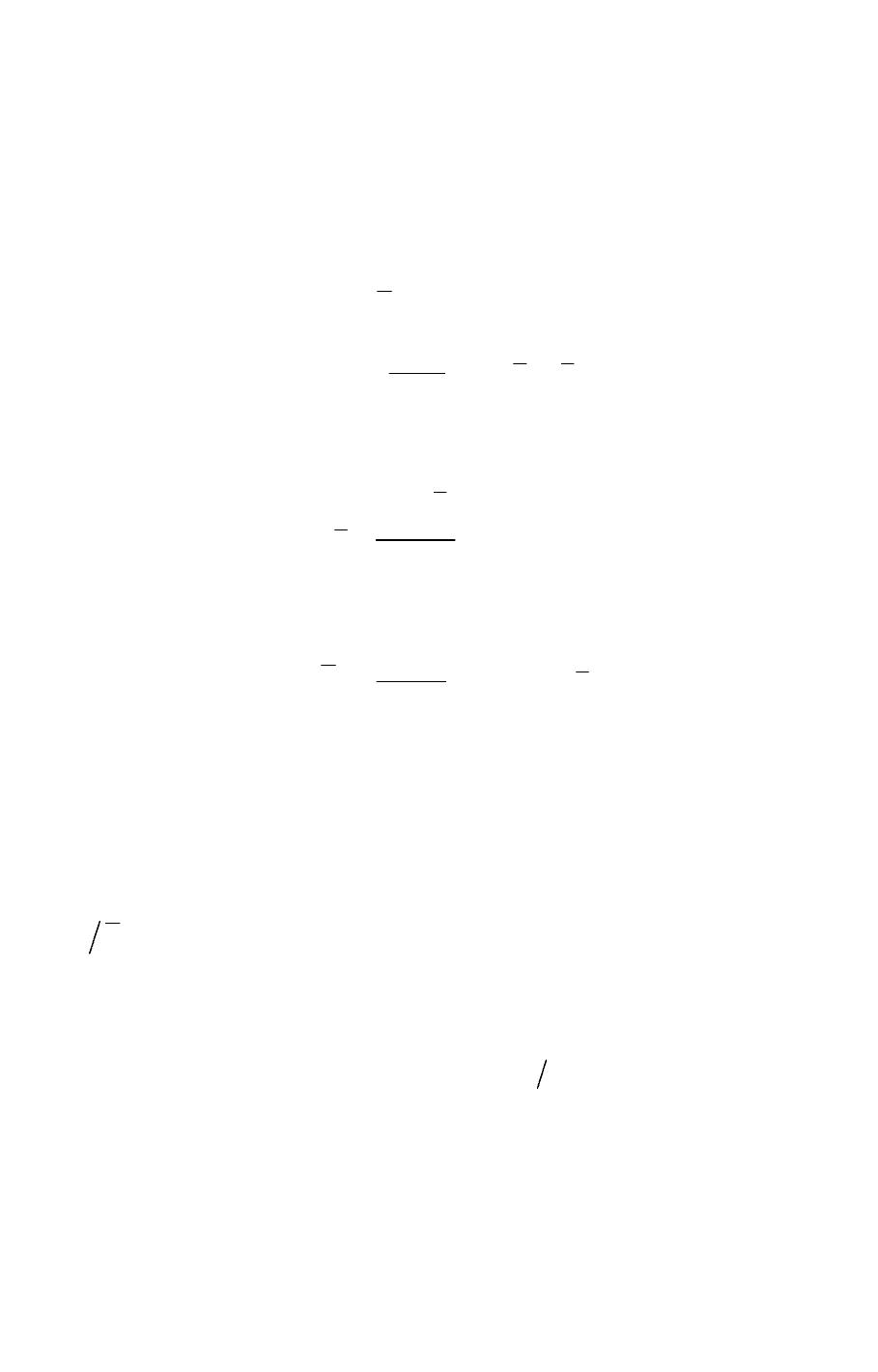
Затем, задаваясь уровнем значимости q, по табл. П-7 для
распределения Стьюдента при числе степеней свободы
2
21
−+= nnk
находим
q
t
. Различие между средними арифметическими считается
допустимым, если
q
tt <
.
При большом числе групп допустимость различия между средними
арифметическими проверяется с помощью критериев Р. Фишера и Э Аббе.
Для применения каждого из них необходимо предварительно проверить,
что все группы имеют одну и ту же дисперсию.
Метод Фишера состоит в сравнении оценок межгрупповой дисперсии
2
L
S
и средней дисперсии групп
2
S
[49]:
( )
∑
=
−
−
=
L
i
iiL
xxn
L
S
1
2
2
1
1
,
где
N
xn
x
L
i
ii
∑
=
=
1
и
∑
=
=
L
i
i
nN
1
(оценка
2
L
S
имеет
1
1
−= Lk
степеней свободы);
( )
∑∑
= =
−
−
=
L
i
n
j
iij
i
xx
LN
S
1 1
2
2
1
(число степеней свободы
LNk −=
2
).
Обе оценки дисперсий имеют
2
χ
-распределение с числом степеней
свободы соответственно
1
k
и
2
k
. Их отношение имеет распределение
Фишера с теми же степенями свободы.
Рассеивание средних арифметических считают допустимым, если
22
SSF
L
=
при выбранной вероятности
α
лежит в пределах
H
F
и
B
F
:
{
}
α=≤≤
BH
FFFP
.
Верхние пределы распределения Фишера F
B
приведены в табл. П-8 и
П-9, нижние находят по соотношению
BH
FF 1=
.Если уровни значимости
при нахождении F
B
и F
H
приняты одинаковыми:
qqq ==
21
, то общий
уровень значимости критерия будет 2q:
q21
−
=
α
.
Метод Аббе менее чувствителен к рассеиванию средних
арифметических, чем метод Фишера, но зато позволяет выявлять
монотонные смещения средних арифметических. Техника применения
этого метода состоит в следующем.

Средние арифметические значения групп следует выписать в
последовательности, соответствующей очередности их получения
,
L
xxx ,...,,
21
.
Затем находим две несмещенные оценки дисперсии группы средних
арифметических: одну — по обычной формуле (3-13)
( )
∑
=
−
−
=
L
i
xx
L
S
1
2
1
2
1
1
1
,
где
∑
=
=
N
i
ii
xn
N
x
1
1
и
∑
=
L
i
i
nN
1
,
вторую — по формуле
( )
∑
−
=
−
=
1
1
22
2
12
1
L
i
i
d
L
S
,
где
,...;
121
xxd −=
,...;
1 iii
xxd −=
+
11 −−
−=
LLL
xxd
.
Отношение
2
1
2
2
SS=ν
должно быть меньше
min
ν
. Критические
значения
min
ν
в зависимости от уровня значимости q и числа групп L
приведены в табл. П-10.
Методика проверки допустимости рассеивания средних
арифметических групп при разных дисперсиях групп доже разработана
(см., например, [55]), но более сложна.
Нужно заметить, что значимое различие между средними
арифметическими может служить как признаком наличия постоянной
систематической погрешности в результатах наблюдений той или иной
группы, так и признаком непостоянства интересующего нас параметра
модели, поставленной в соответствии объекту исследования. Последнее
означает, что постулат
γ
не выполняется и, следовательно, измерение с
требуемой точностью осуществить нельзя.
3-10. Об обработке наблюдений, распределение
которых нельзя считать нормальным
Нормальное распределение служит весьма распространенной моделью
рассеивания наблюдений. Однако иногда эта модель оказывается не
соответствующей экспериментальным данным. Если удается найти другую
модель, т. е. другую функцию распределения, то задачу оценивания
параметров модели, и в том числе истинного значения измеряемой величины,
можно решить на основе принципа максимума правдоподобия. В общем
случае

при известной функции распределения наилучшую оценку измеряемой
величины дает формула Питмэна:
( ) ( )
( ) ( )
∫
∫
∞+
∞−
+∞
∞−
−−
−−
=
duuxfuxf
duuxfuxuf
A
n
n
...
...
~
1
1
.
Дисперсия оценки Питмэна не превышает дисперсию оценки, получаемой
на основе принципа максимума правдоподобия.
Однако чаще всего, если распределение нельзя признать нормальным, то
точно функцию распределения установить не удается. В этом случае, опираясь
на симметричность распределения и используя сведения, приведенные в обзоре
А. И Механникова*
6
, можно рекомендовать следующую схему решения
задачи.
Из результатов наблюдений составляется вариационный ряд, т. е. ряд, в
котором результаты наблюдений расположены в порядке возрастания:
ni
xxx ≤≤≤≤ ......
1
.
В качестве числовой характеристики типа распределения
экспериментальных данных принимают значение
κ
, вычисляемое по формуле
( )
4
1
4
nS
xx
n
i
i
∑
=
−
=κ
,
где S
2
— выборочная дисперсия.
При
4
≥
κ
в качестве оценки измеряемой величины целесообразно
взять оценку медианы, составляемую по полученному вариационному ряду:
+
=
+
+
нечетное.n если ,
четное,n если ,
2
1
~
2
1
1
22
n
nn
x
xx
A
Если
45.2
<
<
κ
, то за оценку измеряемой величины целесообразно
принять среднее арифметическое результатов наблюдений.
6
Механнйков А. И, Методы оперативной обработки результатов наблюдений при
помощи порядковых статистик. — Метрология, 1972, № 4, с 47 — 58.

При распределениях, приближающихся к равномерному (
5.28.1
≤
≤
κ
),
наиболее целесообразной оценкой измеряемой величины надо считать
полуразмах:
2
xx
~
n1
+
=A
.
Критические значения и выбраны несколько условно.
Точность результата можно охарактеризовать длиной
непараметрического доверительного интервала.
Если х
к
и x
n-k+1
— соответственно k-я и (п–k+1)-я порядковые статистики,
составленные по выборке, принадлежащей генеральной совокупности с
непрерывным симметричным распределением, то интервал
[
]
1
,
+−knk
xx
является
доверительным интервалом для центра распределения случайной величины, а
доверительная вероятность равна
{ }
∑
−
=
+−
=<<
kn
ki
l
n
n
knk
CxAxP
2
1
1
.
В частности, при
{ }
{ }
.
2
2
1 3
,
2
1
1 2
2
23
1
12
n
n
n
n
nn
xAxPk
n
xAxPk
++
−=<<=
−
−=<<=
−
−
−
Для
3
>
k
расчетные формулы существенно усложняются. Но для k=4 и
5 можно воспользоваться приближенными соотношениями, приведенными в
упомянутой статье А. И. Механникова:
{ }
{ }
.
2
037.0
1 5
,
2
17.0
14 4
1
4
45
1
3
3
−
−
−
−
−≈<<=
−≈<<=
n
n
n
n
n
xAxPk
n
xAxPk
Рассматривая обработку результатов наблюдений, распределение которых
отличается от нормального, нужно заметить, что, поступаясь эффективностью, в
качестве оценки измеряемой величины практически всегда можно взять среднее
арифметическое результатов наблюдений. Чтобы оценить погрешность
полученного таким образом результата, воспользуемся неравенством Чебышева
{ }
.
1
2
t
tAXP ≤≥− σ
