Рабинович С.Г. Погрешности измерений
Подождите немного. Документ загружается.

где
51
,...,WW — высота столбцов гистограммы; по условию построения
гистограмм площадь всей гистограммы равна единице, т. е. 1
5
1
=
∑
=k
ik
P .
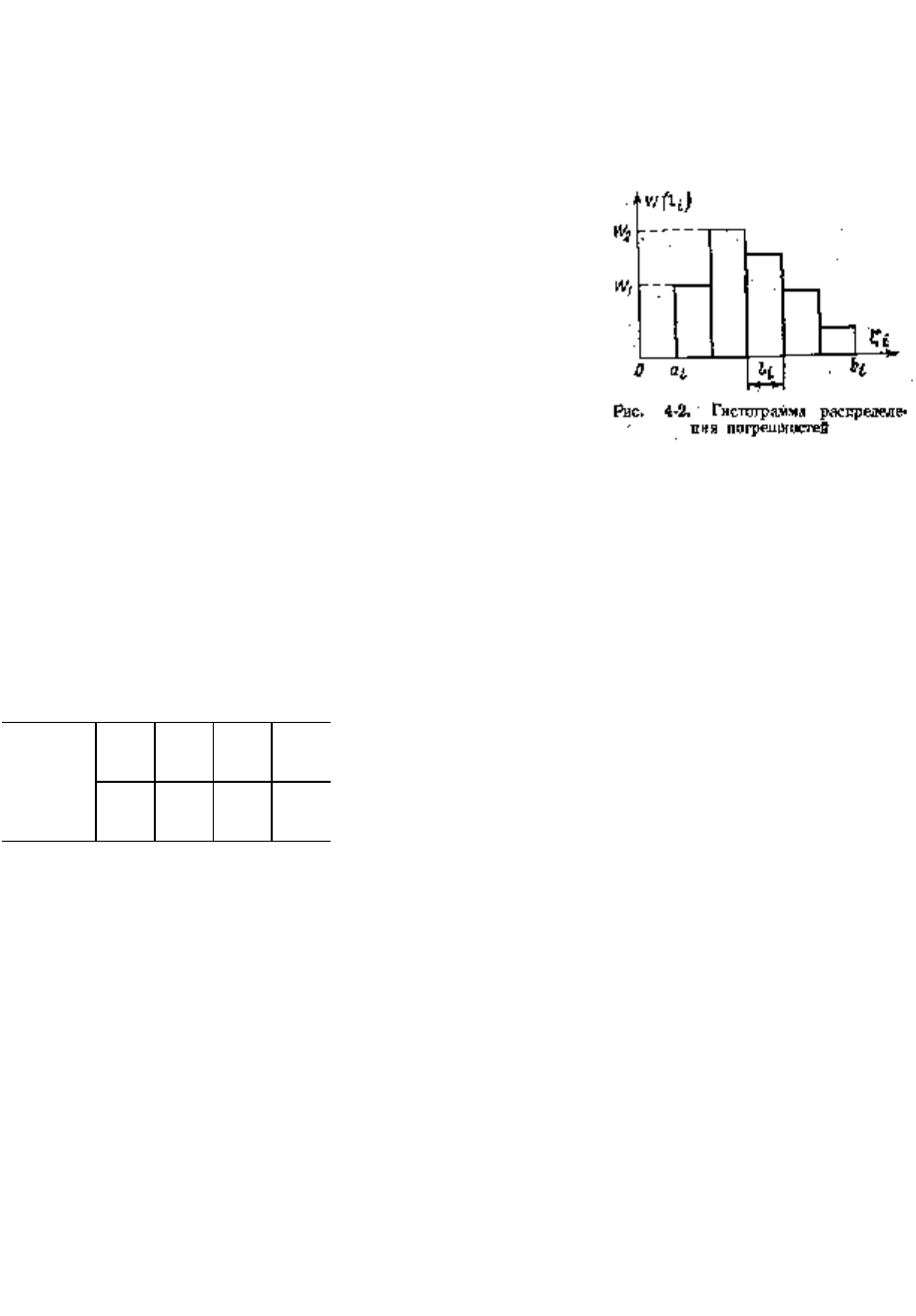
Напомним, что при построении гистограмм (а гистограммы строят по
эмпирическим данным) высоту столбца каждого интервала находят
делением частоты попадания значений в соответствующий интервал на
длину этого интервала. Частота представляет
собой эмпирически полученную оценку
вероятности соответствующего события.
Далее непрерывные случайные величины
представим соответствующими им
дискретными. Для этого середину каждого
интервала l
ik
обозначим a
ik
и введем новую
случайную величину
i
η , которая соответствует
случайной величине
i
ξ таким образом, что
i
η
принимает значение a
ik
с вероятностью p
ik
. Это возможно, так как из
вышесказанного видно, что
∑
=
=
i
m
k
ik
p
1
1
для всех
ni ,...,1
=
.
Полученные данные для каждой случайной величины
i
η
целесообразно представить таблицей следующего вида:
Рассмотрим теперь случайную величину
n
ηηηη +++= ...
21
. Все ее возможные значения
получим перебором всех комбинаций
полученных реализацией a
ik
составляющих
i
η .
Для подсчетов удобно возможные значения случайных величин
выписывать в одну таблицу вида
1
η
11
a
…
i
m
a
1
2
η
21
a
…
i
m
a
2
…
…
…
…
т
η
n
a
1
…
n
nm
a
Затем вычисляем значения случайной величины
η
, отвечающие
каждой из возможных комбинаций реализаций случайных величин
i
η ,
n
nkkki
aaa +++= ...
21
21
η
i
η
1i
a
2i
a
…
i
im
a
1i
p
2i
p
…
i
im
p

и соответствующие им вероятности; последние находим по формуле
{ }
∏
=
====
n
i
iikki
kpaaPp
1
2211
,...,
21
ηη
(4-8)
Сложив затем вероятности, которые соответствуют одной и той же
реализации
ti
a=η
получим вероятности принятия случайной величиной
η
всех
возможных ее значений
N
aa ,...,
1
.
Число комбинаций слагаемых будет
∏
=
n
i
i
m
1
, но поскольку среди них могут
быть совпадающие по значению, то
∏
=
≤
n
i
i
mN
1
,
(4-9)
Полученные данные позволяют построить ступенчатую функцию
распределения
(
)
xF
1
случайной величины
η
:
(
)
{
}
∑
≤==
i
ii
xaaPxF ,
1
η
.
(4-10)
Кривая
(
)
xF
1
является первым приближением к искомой функции
распределения F(х). Полученную ступенчатую кривую можно сгладить методом
линейной интерполяции следующим образом.
Найдем середины интервалов
[
]
1
,
+tt
aa
при
1,...,1
−
=
Nt
:
2
1 tt
t
aa
+
=
+
β
.
(4-11)
Из точек
t
β
восстановим перпендикуляры до пересечения с ломаной линией
(
)
xF
1
. Получим точки с координатами
(
)
xF
t 1
,β
при
1,...,1
−
=
Nt
. К полученным
точкам присоединим точки, в которых функция распределения принимает
значения
(
)
0
01
=βF
и
(
)
1
1
=
n
F β
:
,
1
0
∑
=
=
n
i
i
aβ
∑
=
=
n
i
in
b
1
β
.
(4-12)
Соединив полученные N+1 точек прямыми линиями, получим функцию
(
)
xF
2
,
которая и является искомым приближением.
Приведенный метод дает решение задачи с использованием всей имеющейся
информации и не вносит каких-либо искажений. Однако в общем случае
[
]
[
]
ii
DD ηξ ≠
и дисперсия случайной величины
с
распределением
(
)
xF
1
или F
2
(x)
может отличаться от дисперсии случайной величины
ξ
. Поэтому при условии
независимости слагаемых дисперсию их суммы нужно вычислять обычным путем,
по формуле
[]
()
∑∑
==
=
=
n
i
i
n
i
i
DDD
11
ξξξ
(4-13)

Заметим, что при
5
>
n
распределение суммы слагаемых можно считать
нормальным распределением, которое полностью определяется дисперсией и
математическим ожиданием. Оба эти параметра легко вычисляются по параметрам
слагаемых
[] []
,
1
∑
=
=
n
i
i
MM ξξ
[] []
∑
=
=
n
i
i
DD
1
ξξ
,
и поэтому приведенные выше вычисления целесообразны лишь при числе
слагаемых п <5.
Нужно также заметить, что приведенный способ построения композиции
распределений пригоден и для случая, когда распределения случайных величин
заданы в аналитической форме. При этом плавная кривая, выражающая плотность
распределений случайной величины
i
ξ
заменяется ступенчатой с
i
m
ступенями
так, чтобы ограничиваемая ею площадь, так же как и площадь под плавной
кривой, была равна 1. Если ветви плавной кривой функции распределения
приближаются к оси абсцисс асимптотически, это распределение заменяется
усеченным.
Погрешность, возникающая из-за замены непрерывных распределений
дискретными, как показано в работе [30],
()
∑
=
≤∆
n
i
ii
xfl
1
'2
max
,
где
i
l
— длина интервала, т. е. участка, на котором непрерывный ряд величин
заменен одним значением,
(
)
xf
i
'
max
— максимальное значение производной от
функции плотности распределения
Очевидно также, что данный метод пригоден и для случая дискретных
i
ξ
и
для смешанного случая.
К достоинству метода перебора вариантов нужно отнести то, что он удобен
для выполнения с помощью ЦВМ.
Поясним изложенное примером. Пусть
21
ξξξ += причем
1
ξ подчинена нормальному
закону распределения с плотностью
()
( )
2
2
1
2
2
1
−
−
=
x
exf
π
,
a
2
ξ — закону распределений с равномерной плотностью
(
)
61
2
=xf .
Для нормального распределения с параметрами
2
=
A
и
1
=
σ
область существования
1
ξ
примем равной
[
]
[
]
5;13;3 −=+− σσ AA . Разобьем этот промежуток на 5 интервалов
(
)
5=
i
m ,
симметрично расположенных относительно точки 2 — математического ожидания:
[
]
[
]
[
]
[
]
[
]
[
]
5;5,35,3;5,25,2;5,15,1;5,05,0;15;1 ++++−=− .

Для случайной величины
2
ξ , изменяющейся в промежутке
[
]
3;3− и подчиненной закону
распределения с равномерной плотностью, примем 3
2
=m :
[
]
[
]
[
]
[
]
3;11;11;33;3 +−+−−=− .
Затем вычисляем вероятности попадания случайных величин в соответствующие интервалы. Для
нормального распределения имеем
(
)
( )
( )
∫
∫
∫
==
==
==
−
−
−
−
−
−
−
5,2
5,1
2
2
13
5,1
5,0
2
2
12
5,0
1
2
2
11
.382,0
2
1
,242,0
2
1
,067,0
2
1
dxep
dxep
dxep
x
x
x
π
π
π
Ввиду симметрии нормального распределения
242,0
1214
== pp
,
067,0
1115
== pp
.
Для равномерного распределения
∫
−
−
==
1
3
21
3
1
6
1
dxp
,
∫
−
==
1
1
22
3
1
6
1
dxp
,
∫
==
3
1
23
3
1
3
1
dxp
.
Находим середины построенных интервалов
.2
2
31
,0
2
11
,2
2
13
,25,4
2
55,3
,3
2
5,35,2
,2
2
5,25,1
,1
2
5,15,0
,25,0
2
5,01
23
22
21
15
14
13
12
11
=
+
=
=
+−
=
−=
−−
=
=
+
=
=
+
=
=
+
=
=
+
=
−=
+−
=
a
a
a
a
a
a
a
a
Тем самым определены
1
η , принимающая значения
k
a
1
с вероятностями
k
p
1
, где ,5,...,1=k и
2
η ,
принимающая
Таблица 4-2
Данные перебора вариантов сумм
случайных величин
1
η и
2
η и
соответствующие им вероятности
η
p
-
0,25
-
2=
-
2,25;
-0,25+0=-0,25;
-0,25+2=1,75
0,067x0,333=0,022
1
-
2=
-
1;
1+0=1;
1+2=3
0,242x0,333=0,081
2
-
2=0;
2+0=2;
2+2=4
0,382x0,333=0,127
3
-
2=1;
3+0=3;
3+2=5
0,242x0,333=0,081
4,25-2=2,25
4,25+0=4,25;
4,25+2=6,25
0,067x0,333=0,022
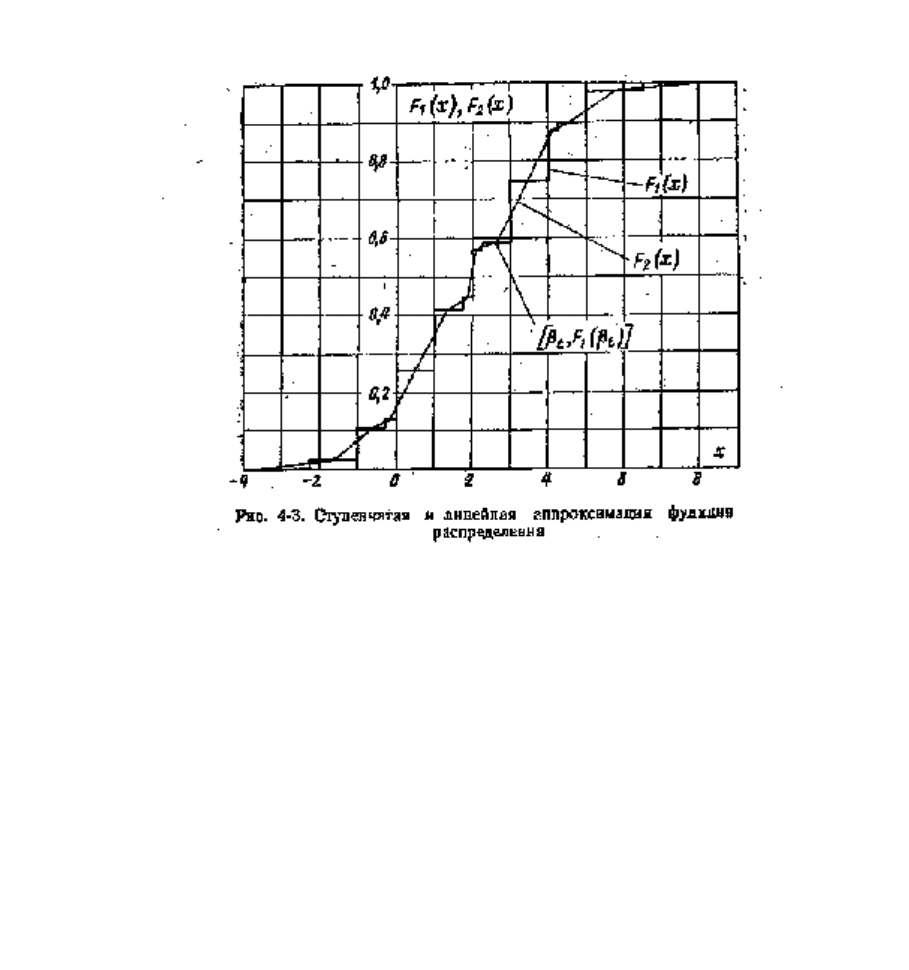
значения
k
a
2
с вероятностями
k
p
2
, где k=1, 2, 3. В результате вычислений получили:
−
−
333,0 333,0 333,0..
2 0 2..
067,0 242,0 382,0 242,0 067.0..
4,25 3 2 1 25,0..
2
2
2
1
1
1
k
k
k
k
p
a
p
a
η
η
Затем переходим к случайной величине
21
ηηη += . Число различных значений
η
оцениваем по формуле (4-9). У нас 5
1
=m , 3
2
=m и
15
≤
N
.
Полученные значения
1
η и
2
η представим в форме таблицы:
1
η
… -0,25 1 2 3 4,25
2
η
… -2 0 2 – –
Пользуясь этой таблицей, находим значения
21
ηηη += . Порядок расчетов ясен из табл. 4-2.
Затем располагаем значения
t
η в порядке возрастания. Каждому значению
t
η отвечает своя
вероятность
t
p . Если одно и то же значение
t
η встречается несколько раз, то вероятность данного
значения находится как сумма этих вероятностей. Получаем
t
η
… -2,25 -1 -0,25 0 1 1,75 2
t
p
… 0,022 0,081 0,022 0,127 0,162 0,022 0,127
t
η
… 2,25 3 4 4,25 5 6,25
t
p
… 0,22 0,162 0,127 0,022 0,081 0,022
Tax как 1
1
=η и 2
2
=η встречались по два раза, то
13
=
N
.
По полученным данным, используя (4-10), нетрудно построить
(
)
xF
1
. Значения этой функции в
найденных промежутках приведены в табл. 4-3, а соответствующий график представлен на рис. 4-3 в
виде ступенчатой линии.
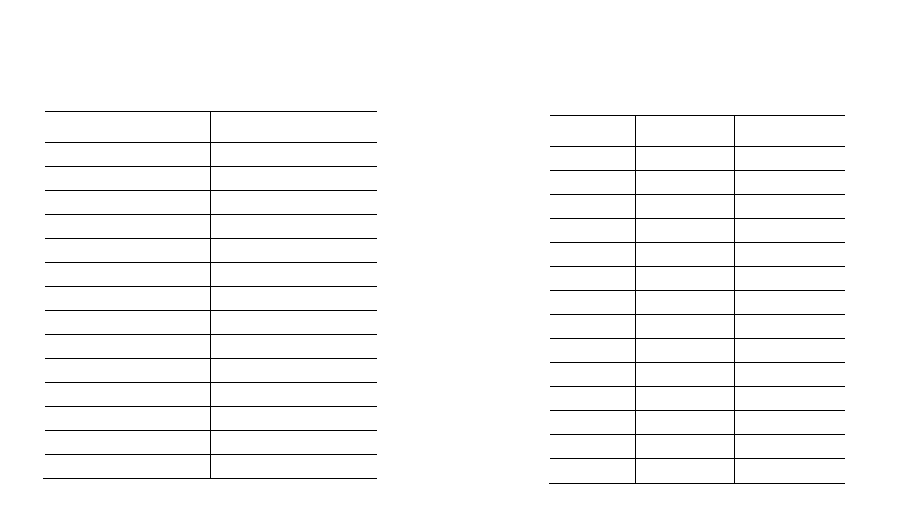
Таблица 4-3
Данные ступенчатого приближения к функции
распределения суммы двух рассматриваемых
случайных величин
x
(
)
xF
1
−∞
;
-
2,25
0,0
-
2,25;
-
1,00
0,022
-
1,00;
-
0,25
0,103
-
0,25; 0,00
0,125
0,00; 1,00
0,252
1,00;
1,75
0,414
1,75; 2,00
0,436
2,00; 2,25
0,563
2,25; 3,00
0,585
3,00; 4,00
0,747
4,00; 4,25
0,874
4,25; 5,00
0,896
5,00; 6,25
0,978
6,25;
∞
1,0
Таблица 4-4
Данные линейного приближения к функции
распределения суммы двух рассматриваемых
случайных величин
t
t
β
(
)
xF
2
0
-
4,00
0,00
1
-
1,62
0,022
2
-
0,62
0,103
3
-
0,14
0,125
4
0,50
0,252
5
0,14
0,414
6
1,87
0,436
7
2,12
0,563
8
2,62
0,585
9
3,50
0,747
10
4,12
0
,874
11
4,62
0,896
12
5,62
0,978
13
8,0
1,0

По (4-11) находим
i
β для
12
,...,
1
=
i
, а по (4-12) определяем
0
β и
13
β . Используя эти
вычисления, а также данные табл. 4-3, строим функцию распределения F
2
(х). График
(
)
xF
2
представлен на рис. 4-3 в виде ломаной линии, соединяющей точки
(
)
[
]
tt
F ββ
1
, , при
13
,...,
0
=
t
.
Числовые значения
(
)
xF
2
при 13,...,0, == tx
t
β представлены в табл. 4-4.
Как уже было отмечено, приближение
(
)
xF
2
к предельной функции распределения
(
)
xF можно
улучшить путем уменьшения интервалов разбиения областей изменения исходных случайных
величин.
Интересно отметить, что изложенное решение позволяет находить края функции
распределения
(
)
xF
2
без построения всей функции, что в ряде случаев и составляет основную
задачу.
ПРЯМЫЕ ИЗМЕРЕНИЯ
5-1. Методы обработки результатов наблюдений
при прямых статистических
измерениях
Рассмотрим прежде всего статистические
измерения, при которых многократные
наблюдения выполняются с целью
уменьшения влияния случайных
погрешностей. Результат каждого наблюдения
при этом дает оценку измеряемой величины.
Результат наблюдения отличается от
истинного значения измеряемой величины из-
за случайной
i
ψ и систематической
i
ϑ , составляющих погрешности:
iii
Ax ϑψ ++=
'
.
ГЛАВА ПЯТАЯ

Повторяя наблюдения, мы получаем информацию о случайной
погрешности. О систематической погрешности из самих наблюдений
информацию извлечь нельзя. Чтобы оценить эту погрешность, надо знать
свойства используемых средств измерений, метод измерения и условия
измерения.
Предположим, что систематическая погрешность результата каждого
наблюдения известна. Тогда, введя поправки
ii
С ϑ−= , вместо группы
'
i
x
получим группу исправленных результатов наблюдений
ii
Ax ψ+= .
Наша задача найти оценку
(
)
i
xfA = . Математически обоснованное
решение, отвечающее требованиям несмещенности, состоятельности и
эффективности, можно найти, зная вид распределения
i
x . Часто
погрешности измерений можно считать имеющими нормальное
распределение. То же самое распределение имеют и результаты
наблюдений. Соответствие полученных данных нормальному
распределению можно проверить методами, приведенными в § 3-4.
При нормальном распределении наблюдений, как показано в § 3-3,
оптимальной оценкой центра распределения А является среднее
арифметическое результатов наблюдений
n
x
A
n
i
i
∑
=
=
1
'
~
.
Если систематические погрешности
0
ϑϑ =
i
, т, е. они постоянны, то
можно не исправлять результатов наблюдений, а сначала вычислить
предварительный результат измерения
0
1
'
~~
ϑ+==
∑
=
A
n
x
A
n
i
i
,
а затем найти CAAA +=−=
'
0
'
~
~
~
ϑ , где
0
ϑ−=C есть поправка.
Как отмечалось, среднее арифметическое результатов наблюдений
является несмещенной, состоятельной и эффективной оценкой истинного
значения измеряемой величины лишь при нормальном распределении
наблюдений. Однако независимо от вида распределения погрешностей
измерений среднее арифметическое обладает двумя важными
особенностями.
1. Сумма отклонений от среднего арифметического равна нулю.
Пусть
n
xx ,...,
1
— группа результатов наблюдений, среднее
арифметическое
x
. Составим разности xx
i
− для всех ni ,...,1
=
и найдем их
сумму:
( )
∑∑∑
===
−=−
n
i
n
i
i
n
i
i
xxxx
111
.
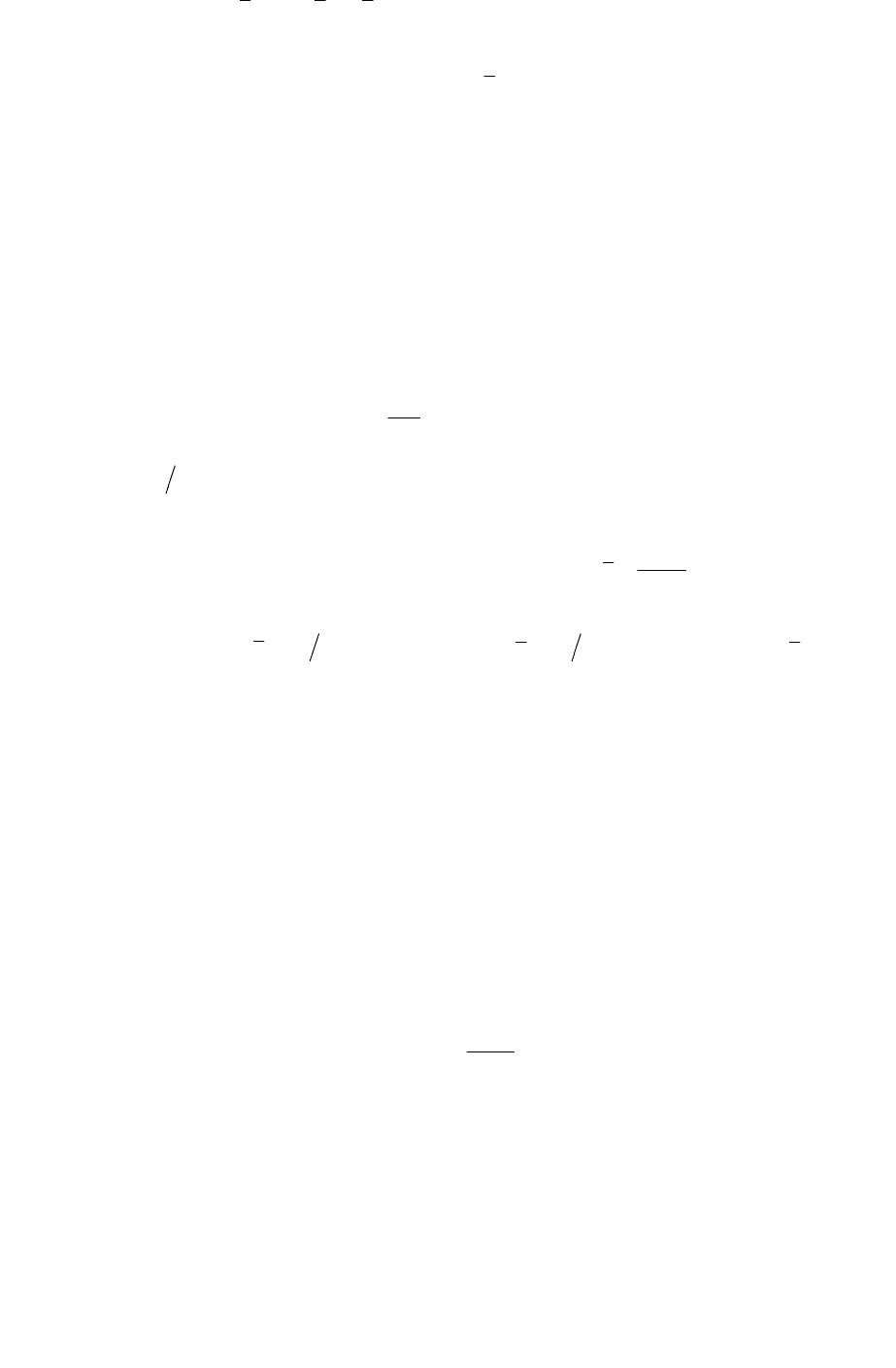
Так как
∑
=
=
n
i
i
xnx
1
и
∑
=
=
n
i
xnx
1
, то
( )
∑
=
=−
n
i
i
xx
1
0.
Этим свойством следует пользоваться при расчетах для контроля
правильности вычислений.
3. Сумма квадратов отклонений от среднего арифметического минимальна.
Рассмотрим функцию
(
)
∑
=
−=
n
i
i
AxQ
1
2
~
.
Найдем А так, чтобы минимизировать Q. Для этого найдем
(
)
∑
=
−−=
n
i
i
Ax
Ad
dQ
1
~
2
~
и положим 0
~
=AddQ ; отсюда получим
( )
n
x
xAетAnxAx
n
i
i
n
i
i
n
i
i
∑
∑∑
=
==
====−
1
11
~
..,
~
,0
~
.
Так как при
xA <
~
0
~
<AddQ , а при
xA >
~
0
~
>AddQ ,
то при
xA =
~
: имеем
минимум Q.
Хотя сумма квадратов отклонений от среднего арифметического
минимальна, но это лишь означает, что в классе оценок, являющихся линейной
функцией результатов наблюдений, среднее арифметическое — наиболее
эффективная оценка измеряемой величины. Абсолютно эффективной эта оценка
становится при нормальном распределении погрешностей. При других
распределениях, как отмечалось в гл. 3, известны оценки более эффективные, чем
среднее арифметическое. Понятно, эти оценки уже не являются линейной
функцией результатов наблюдений.
Итак, в качестве оценки измеряемой величины мы имеем
n
x
A
n
i
i
∑
=
=
1
~
.
(5-1)
Из-за случайных погрешностей результаты наблюдений также являются
случайными величинами, и если выполнить еще одну серию наблюдений, то
полученное новое среднее арифметическое будет несколько отличаться от ранее
найденной оценки.
Это чаще всего ненаблюдаемое, но, несомненно, реальное рассеивание
средних арифметических характеризуется или дисперсией средних
арифметических, или средним квадратическим отклонением. В соответствии с
формулой (3-16) по данным эксперимента

находят оценку среднего квадратического отклонения среднего
арифметического
( )
( )
1
1
2
−
−
=
∑
=
nn
xx
S
n
i
i
x
.
(5-2)
Кроме того, для А можно построить доверительный интервал, определяющий
доверительные границы случайной погрешности результата измерения.
Доверительный интервал определяется неравенствами
xx
AAA ψψ +≤≤−
~
~
,
где
xqx
St=ψ ,
q
t — q-процентная точка распределения Стьюдента, зависящая от
доверительной вероятности
α
и числа степеней свободы
1
−
=
nk
(см. табл. П-7).
Неравенства, определяющие границы доверительного интервала для А,
можно несколько преобразовать, с тем чтобы определить границы случайной
погрешности результата измерения. Из приведенных неравенств следует,
что
x
AA ψ≥−
~
и AA
x
−≤−
~
ψ .
Следовательно, случайная погрешность
ψ
с вероятностью, равной
доверительной вероятности
α
, лежит в границах
x
ψ± :
xqx
St=ψ .
(5-3)
Как видно из изложенного, случайные погрешности и доверительные
границы этих погрешностей можно оценить по данным, получаемым в
результате повторных наблюдений при одном и том же измерении.
С систематическими погрешностями дело обстоит иначе. Смещенность
результата измерения, которую характеризуют систематические погрешности,
можно оценить либо с помощью более точных средств измерений, либо по
косвенным данным, включая данные о метрологических свойствах используемых
при измерении средств измерений.
Первый вариант — применение более точных средств измерений —
используется, как правило, только в поверочной практике. В других случаях
использовать параллельно в одних и тех же условиях приборы разной
точности нецелесообразно. Поэтому основным является второй вариант, когда
систематическая погрешность оценивается по косвенным данным. Для этого
выясняют все возможные источники погрешностей, оценивают по отдельности
погрешности, вызванные каждым из них, т. е. оценивают все элементарные
погрешности, и их суммируют. В зависимости от обстоятельств, перечисленные
задачи решают по-разному. Рассмотрим сначала измерения с точным оцениванием
погрешностей.
