Рабинович С.Г. Погрешности измерений
Подождите немного. Документ загружается.


что их систематические погрешности, разные у разных приборов, будут
как-то компенсировать друг друга и погрешность получаемого результата
будем меньше, чем при применений отдельного прибора. При этом
систематические погрешности приборов можно рассматривать как
реализации случайной величины.
В тех случаях, когда для измеряемой величины известны некоторые
точные соотношения ее с другими величинами, эти соотношения можно
использовать для уменьшения погрешности измерения. Например, если
измеряют углы плоского треугольника, то нужно учесть, что их сумма
равна 180°.
4-3. Предпосылки оценивания систематических
погрешностей
Как следует из изложенного, в связи с систематическими
погрешностями решаются две задачи: а) нахождение поправок и
б) оценивание границ (или других параметров) систематических
погрешностей.
Поправки имеют определенный знак, и их суммирование, а также
учет не вызывает затруднений. Сами значения поправок находят
разнообразными путями. Поправки, обусловленные систематическими
погрешностями средств измерений, определяют по результатам поверок
последних. Во многих случаях для этого средства измерений специально
поверяют непосредственно перед применением.
Поправки для учета тех или иных влияющих величин вычисляют при
известных коэффициентах или функциях влияния на основе данных
вспомогательных измерений этих величин. При установлении функций
влияния и коэффициентов влияния полезны методы корреляционного и
регрессионного анализа [1].
Конкретные методы нахождения поправок очень разнообразны, и мы
не будем на них останавливаться. Впрочем, наиболее характерные из них
использованы в примерах, разбираемых ниже и в следующих главах.
Пример. Измерение напряжения с помощью вольтметра. Внутреннее
сопротивление источника напряжения
1060 ±=
i
R
Ом. Вольтметр кл. 0,5
с верхним пределом диапазона показаний 16 В. Сопротивление
вольтметра
5=
V
R
кОм и известно с погрешностью в пределах
%5.0
±
.
Показание вольтметра 12,35 В. Найдем поправку, которую нужно внести в
показание прибора.
Показания вольтметра соответствуют падению напряжения на нем
x
Vi
V
V
U
RR
R
U
+
= .
Относительная погрешность, обусловленная ограниченным
сопротивлением
V
R (погрешность методическая), в процентах равна
%2.1
5060
60100100
%100
%
−=
⋅
−=
+
−=⋅
−
=
Vi
i
x
xV
RR
R
U
UU
ε

Эта погрешность существенна, и, следовательно, ее нужно учесть.
Поправка равна погрешности с обратным знаком: %2.1
%%
+=−= εC или в
единицах измеряемой величины
146.035.12102.1
2
+=⋅⋅=
−
V
C
В.
Погрешность полученного значения поправки определяется
погрешностью, с которой известно сопротивление
i
R , и ее предельное
значение равно %17100
60
10
=⋅ . Погрешностью из-за неточности оценки
внутреннего сопротивления вольтметра, очевидно, можно пренебречь.
Следовательно, 03.0146.017.0 ±≈⋅±=∆
U
В и поправка, которую нужно
внести в показания вольтметра, с учетом округления будет 15.0+=
V
C В.
Таким образом, 50.1215.035.12
~
=+=
x
U В. Этот результат имеет
определенную погрешность, в том числе неисключенный остаток
погрешности из-за потребления некоторой мощности вольтметром,
лежащий в пределах 03.0±=∆
U
В или %24.0
%
±=δ .
В рассмотренном примере неточность поправки задана путем указания
границ погрешности ее определения.
Вторая задача более специфична. Вне зависимости от того, к какой
категории относится измерение (является оно прямым, косвенным,
совместным или совокупным), систематическая погрешность результата
оценивается, как правило, по ее составляющим. Для части этих
составляющих заранее известны определенные параметры, для части же
их они вычисляются по вспомогательным данным. Так, для погрешности
измерения, обусловленной основной погрешностью используемых при
измерении средств, обычно известны границы. Составляющие
погрешности, обусловленные отклонением каждой из влияющих величин
от ее нормального значения, вычисляются. При этом обычно находят
границы каждой из этих погрешностей.
Составляющие, из которых складывается систематическая
погрешность результата измерения, будем называть элементарными
систематическими погрешностями.
Если для части составляющих погрешности измерения находят их
оценки и эти погрешности устраняются путем введения поправок, то в
качестве рассматриваемых элементарных погрешностей выступают
погрешности определения поправок. Последние также характеризуют их
границами.
Таким образом, для оценивания систематической погрешности
результата измерения необходимо уметь суммировать ее элементарные
составляющие.
В конкретном измерении каждая элементарная систематическая
погрешность получает конкретную реализацию. Поскольку речь идет о
систематических погрешностях, то реализация систематической

погрешности результата
ϑ
представляет собой алгебраическую сумму
реализаций ее составляющих
(
)
n
i
,...,1=ϑϑ
:
∑
=
=
n
i
i
1
ϑϑ
.
При повторном измерении той же величины тем же методом, но в
другой лаборатории, с использованием других средств измерений (хотя и
того же типа) составляющие систематической погрешности примут другие
значения.
Если иметь в виду множество возможных измерений данной
величины, то элементарные систематические погрешности нужно
рассматривать как реализации случайных величин и суммировать
методами, разработанными в теории вероятностей и математической
статистике.
О необходимости статистического суммирования элементарных
систематических погрешностей говорит и интуиция, основанная на опыте.
Пусть, например, систематическая погрешность результата измерения
складывается из пяти одинаковых составляющих:
%1...
521
==== θθθ
Очевидно, что оценку систематической погрешности результата,
равную арифметической сумме составляющих, т. е.
%5
=
θ
, мы не
примем, основываясь просто на здравом смысле, который говорит, что
случай, когда все составляющие одновременно примут свои крайние
значения, слишком маловероятен.
Математические методы суммирования случайных величин
предполагают известными функции их распределений. Однако для
элементарных систематических погрешностей функции распределений,
как правило, неизвестны. Тем не менее задача оценивания,
систематической погрешности результата измерения должна быть решена.
Поэтому, если функции распределений элементарных систематических
погрешностей неизвестны, то суммирование нужно выполнить, задавшись
формой этих распределений. Естественно, сами распределения нужно
связать с известными оценками параметров этих распределений.
На первый взгляд может показаться, что полученная таким образом
оценка погрешности не заслуживает доверия. В действительности, однако,
это не так. При выборе формы распределения каждой из элементарных
погрешностей используется информация о ее природе, что дает очень
много. Кроме того, в соответствии с принципом оценивания погрешностей
сверху из возможных форм распределений данной погрешности всякий
раз выбирают наихудшую форму функции распределения. Если эти
соображения учитываются, то получаемая оценка погрешности достаточно
надежно характеризует неопределенность результата измерения.

Другой вариант решения задачи — потребовать экспериментального
нахождения распределений составляющих систематических погрешностей. Это
требование легко сформулировать, но практически нельзя выполнить.
Проблематична вообще целесообразность специальной постановки сложных
экспериментов с целью уточнения оценки погрешности, а не результата самого
измерения.
По существу, элементарные систематические погрешности могут иметь
самую различную форму распределений. Когда сведения о природе той или
иной погрешности не позволяют установить форму распределения, можно
руководствоваться следующим практическим правилом: если известна оценка
границ какой-то погрешности, ее распределение следует считать
равномерным; если известна оценка среднего квадратического отклонения
погрешности, распределение следует считать нормальным. Приведенная
рекомендация выработана на основе здравого смысла и интуиции.
Интересно отметить, что при известных границах равномерное
распределение обладает максимальной энтропией, а при известных дисперсии
и математическом ожидании максимальной энтропией обладает нормальное
распределение*
7
.
Применение приведенного правила позволяет статистически суммировать
элементарные систематические погрешности и обычно приводит к достаточно
осторожным и вместе с тем не слишком завышенным оценкам погрешности
результата измерения.
Как уже отмечалось, для элементарных систематических погрешностей в
большинстве случаев оценивают их границы. В соответствии с приведенным
правилом при отсутствии дополнительной информации эти погрешности
рассматривают как случайные величины, имеющие, равномерное
распределение.
Соображения относительно выбора функций распределения для
некоторых конкретных элементарных систематических погрешностей
приведены в работе [41].
Статистическое суммирование элементарных погрешностей производится
путем построения композиции их распределений. Однако для практики
необходимы простые способы решения этой задачи.
Самый простой вариант возможен при большом числе слагаемых, так как
в этом случае результирующее распределение обычно всегда можно считать
нормальным. Для того чтобы найти это распределение, достаточно вычислить
его дисперсию. Последняя находится как сумма дисперсий составляющих, и
нужно лишь по имеющимся данным о составляющих вычислить оценки их
дисперсий.
7
Клюев Н. И. Информационные основы передачи сообщений. M.: Советское
радио, 1966. 360 с., ил., и др.

Наибольшие трудности составляет решение задачи при суммировании
сравнительно небольшого числа слагаемых, когда форма результирующего
распределения заранее неизвестна. Простые методы решений этой задачи
рассматриваются ниже.
Классификация ситуаций на случаи с большим или малым числом
слагаемых несколько условна и зависит от формы распределений составляющих
погрешности и от их параметров. Так, два одинаковых слагаемых с треугольным
распределением в сумме дают распределение, весьма близкое к нормальному.
Однако, чтобы получить распределение, близкое к нормальному, при
суммировании арккосинусных распределений нужно примерно десять
слагаемых.
На практике часто при суммировании малого числа погрешностей (двух-
трех) прибегают к арифметическому сложению составляющих. Такой способ
дает, как известно, преувеличенную погрешность и применяется, по-видимому, с
целью компенсации возможного приуменьшения элементарных погрешностей.
Последнее весьма вероятно, так как в рассматриваемом случае, когда
складываются всего две-три погрешности, часто определяющими оказываются
основные погрешности примененных средств измерений. Их границы
принимают равными пределу допускаемой погрешности. Но если после поверки
до измерения прошло значительное время или при поверке применялись
образцовые средства с недостаточно большим запасом по точности, то
фактические погрешности используемых средств измерений в момент
применения могут оказаться больше допускаемых для них пределов.
По мнению автора, следует более строго оценивать слагаемые и их
суммирование выполнять статистически, на основе вероятностных
представлений, отвечающих механизму образования погрешности результата
измерения.
4-4. Суммирование элементарных
систематических погрешностей в предположении
равномерного распределения слагаемых
При оценивании систематической погрешности результата измерения
часто возникает задача построения композиции равномерных распределений.
Теоретическое решение этой задачи известно и приведено, например, в книге
[12]. Для нас интересно выяснить возможность упрощенного решения
применительно к рассматриваемой прикладной задаче.
Рассмотрим п случайных величин
i
x
(
)
ni ,...,1=
, каждая из которых
имеет равномерное распределение с центром О на интервале
+−
2
1
;
2
1
.
Введем обозначение
∑
=
=
n
i
i
x
1
ϑ
.
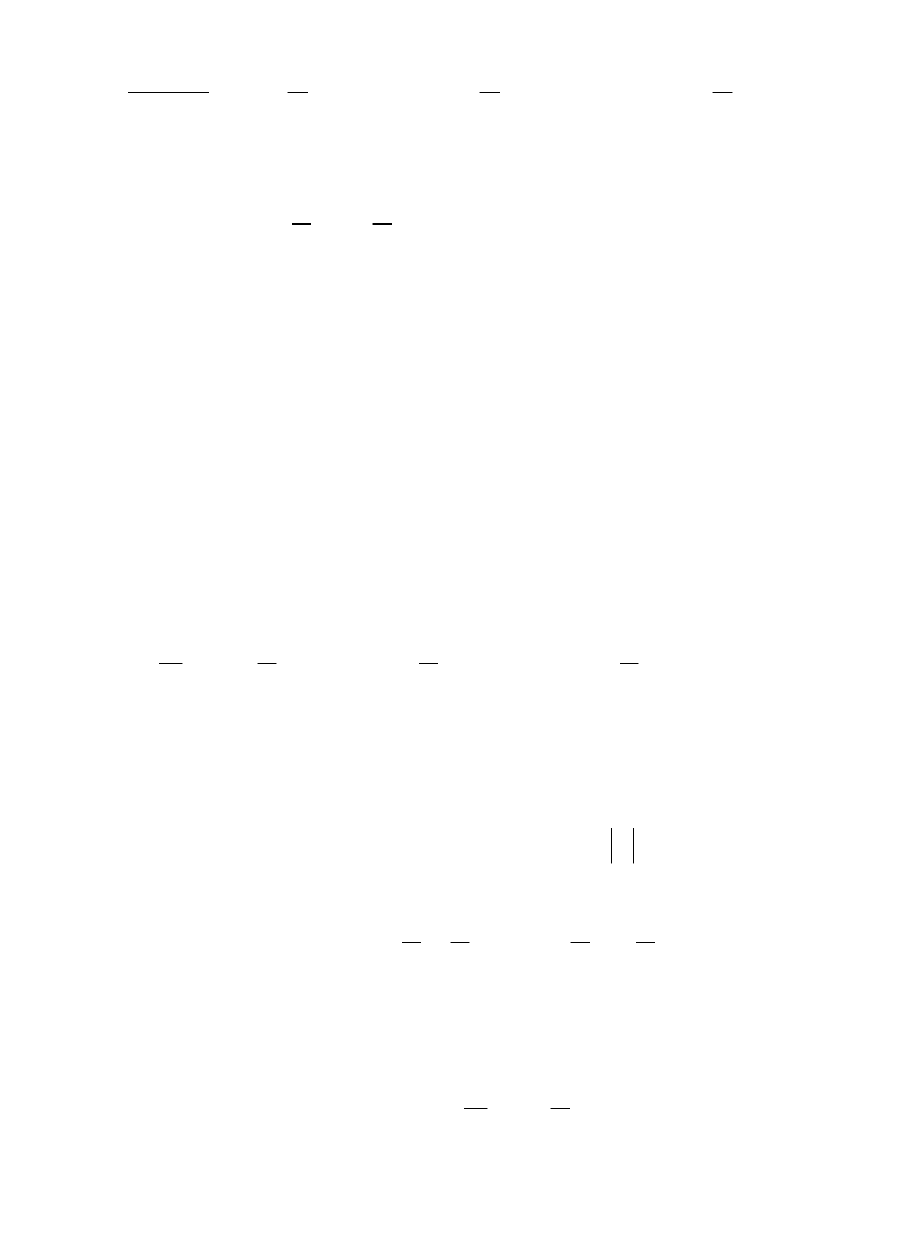
Функции плотности распределения суммы этих случайных величин
имеют вид:
()
( )
+
−++
−+−
+
−
=
−−−
...1
2
1
22!1
1
1
2
1
1
1 n
n
n
n
n
n
n
C
n
C
n
n
f ϑϑϑϑ
причем в эту сумму следует включать только те слагаемые, в которых
основания степени
1
2
,
2
−++
nn
ϑϑ
и т. д. при данном п неотрицательны;
например, если п=2, то
() ( )
<≤−
≤<−+
=−+=
.10 ,1
;01 ,1
21
2
ϑϑ
ϑϑ
ϑϑϑf
Плотность распределения суммы двух слагаемых имеет вид треугольника.
При п=3 график
(
)
nf
3
составляется из трех отрезков квадратичных парабол
и внешне очень похож на кривую нормального распределения. При п=4 эта
функция распределения почти неотличима от нормальной.
Имея уравнение для плотности распределения, нетрудно найти
интегральную функцию распределения
()
+
−++
−+−
+= ...2
2
1
22!
1
21
n
n
n
n
n
n
n
C
n
C
n
n
F ϑϑϑϑ
.
(4-1)
Однако для практики желательно иметь более простое и наглядное
решение. Его можно найти, если учесть, что в соответствии с принципом
оценивания погрешностей сверху нас интересуют такие границы
θ
±
для
суммы составляющих, при которых вероятность
{
}
.9,0>≤θϑP
Имея в виду последнее замечание, рассмотрим функцию распределения
(
)
ϑ
n
F
на крайних интервалах
+−− 1
2
,
2
nn
и
−
2
,1
2
nn
.
Уравнение (4-1) для одного участка принимает вид
()
n
n
n
n
F
+=
2!
1
ϑϑ
.
Композиция распределений симметрична относительно оси ординат.
Поэтому рассмотрим одну ее ветвь, например левую,
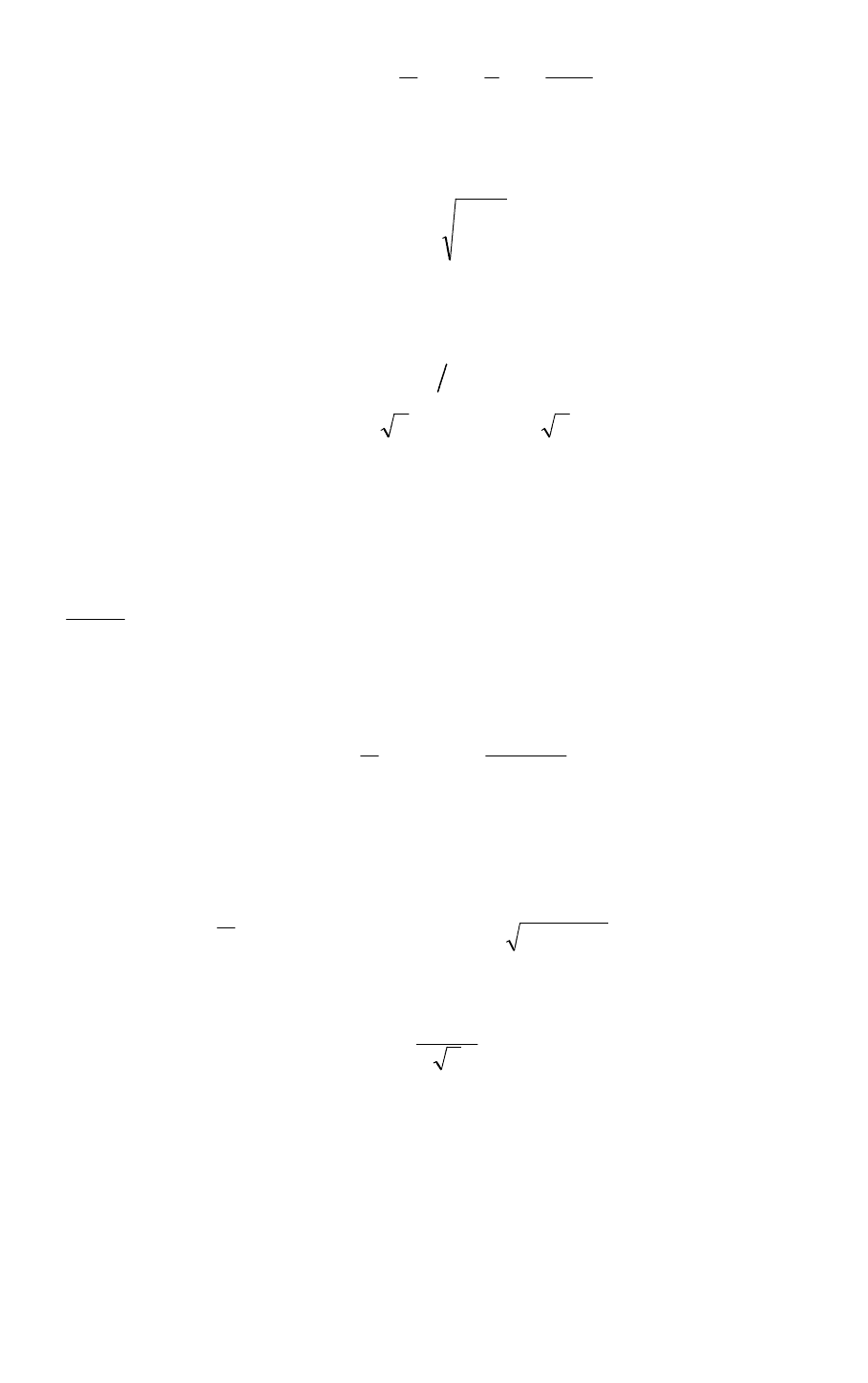
отвечающую условию
θ
ϑ
−
≤
−
. Для доверительной вероятности
α
получим условие
( )
2
1
2!
1 α
θθ
−
=
+−=−
n
n
n
n
F ,
(4-2)
из которого можно вычислить
θ
.
Представим найденные по формуле (4-2) значения
θ
в следующем виде:
∑
=
=
n
i
i
k
1
2
θθ
,
(4-3)
где
i
θ
— граница интервала, в пределах которого изменяется
i
x
(
)
iii
x θθ +≤≤−
,k — поправочный коэффициент.
В рассматриваемом случае
21=
i
θ
для всех
,,...,1 ni
=
т. е.
2/nk=θ и nk /2θ= .
(4-4)
Формула (4-3) удобна для вычислений, и поэтому исследуем, как
коэффициент k зависит от
α
и от п. Схема расчетов такова. По уравнению
(4-2), задаваясь
α
и п, найдем
θ
. Затем по формуле (4-3) или (4-4) найдем
соответствующий данным
α
и п коэффициент k. Например,
α
=0,99, п=4. При
этом
2
1
α
−
=0,005. Проверим, лежит ли
θ
, соответствующее этой вероятности, в
пределах крайнего левого интервала [-2, -1]. Для этого найдем вероятность,
отвечающую самому большому значению
ϑ
в этом интервале, т. е. F
4
(-1):
( )
041,0
4
3
2
1
1
21
!
4
1
)1(
4
4
=
⋅⋅⋅
=+−=−F .
Так как 0,005<0,041, то интересующее нас значение
θ
лежит в данном
интервале.
Подставляя исходные данные в уравнение (4-2), находим
θ
:
( )
;005,02
!
4
1
4
=+−θ
;005,0242
4
⋅=+−θ
41,1
=
θ
.
Найдя
θ
, по формуле (4-4) получаем
41,1
4
41,12
=
⋅
=k
.
Аналогично были вычислены значения k для других
α
и
n
,
представленные в табл. 4-1.
Значение k для
∞
→
n
было найдено с использованием того, что при этом
результирующее распределение можно считать нормальным:
∑
=
=
n
i
i
x
1
ϑ ,
[] []
∑∑
==
=
=
n
i
i
n
i
i
xDxDD
11
ϑ
.
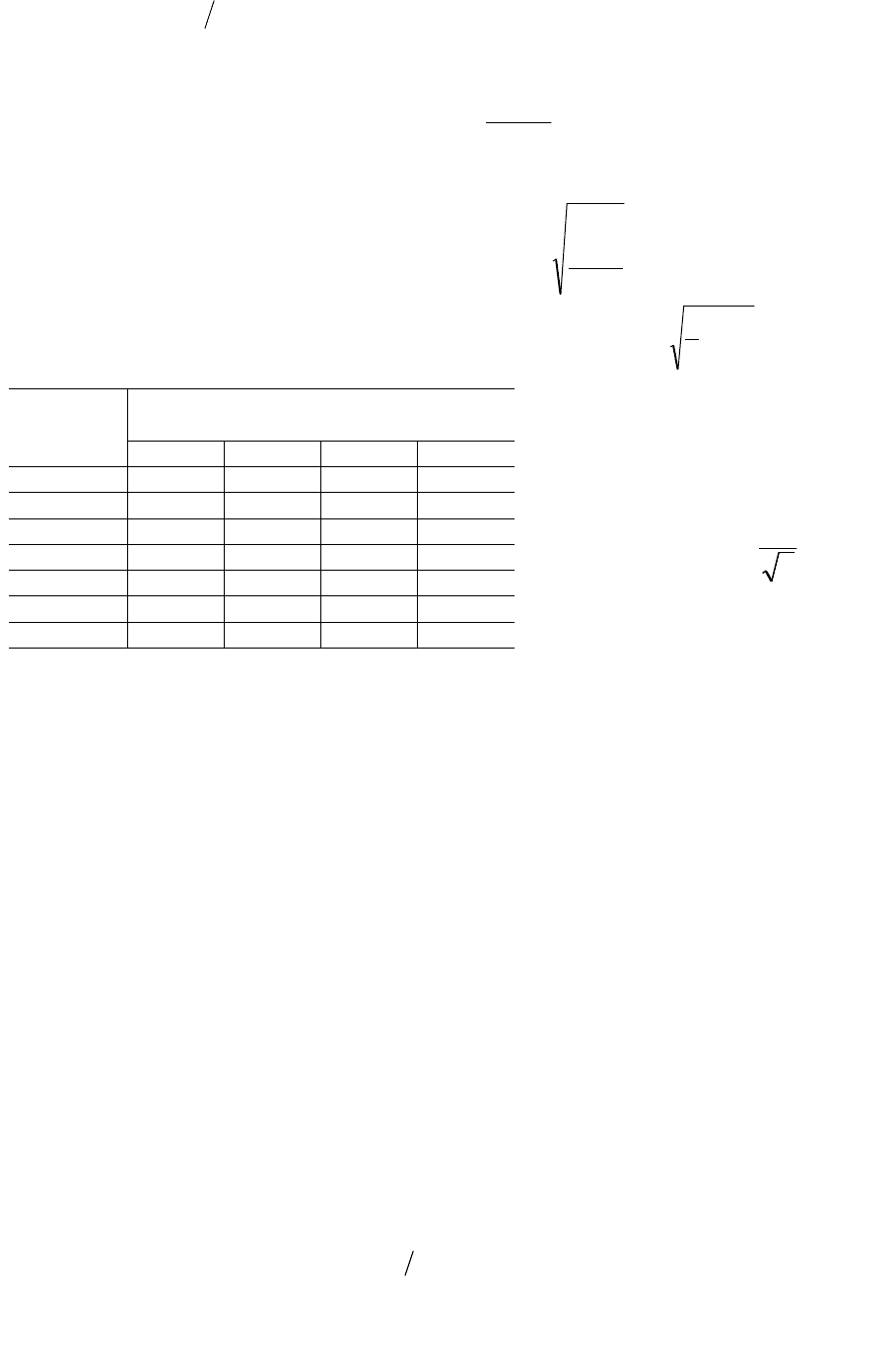
Ho
[
]
3
2
ii
xD θ= . Следовательно,
[]
3
1
2
∑
=
=
n
i
i
D
θ
ϑ
Граница доверительного интервала для случайной величины с
нормальным распределением при
3
1
2
∑
=
=
n
i
i
θ
σ и
0
=
A
равна
∑
=
==
n
i
i
zz
1
2
3
1
θσθ
αα
.
Сравнивая данное
выражение с выражением (4-
3), получаем
3
α
z
k
n
=
∞→
.
Обращаясь к полученной
таким образом таблице,
нужно отметить как как
примечательное свойство
коэффициента k, что при
99,0
≤
α
он мало зависит от
числа слагаемых. Этим свойством можно воспользоваться и принять для k
усредненные значения [43]:
α
…
0,90 0,95 0,98 0,99
k …
0,95 1,1 1,3 1,4
Погрешность от применения усредненных значений k, как видно из их
сравнения с точными значениями, приведенными в табл. 4-1, не превышает
10%.
Малое влияние числа слагаемых косвенно означает, что предполагавшееся
при вычислениях равенство всех
i
θ не является обязательным. Так, если
уменьшать одно из слагаемых
i
θ , то в пределе вместо п получим п-1
слагаемых. Значение же коэффициента k при этом практически не изменится.
Если, наоборот, одно из слагаемых будем постепенно увеличивать, то, как
показано в работе [34], коэффициент k при этом будет уменьшаться.
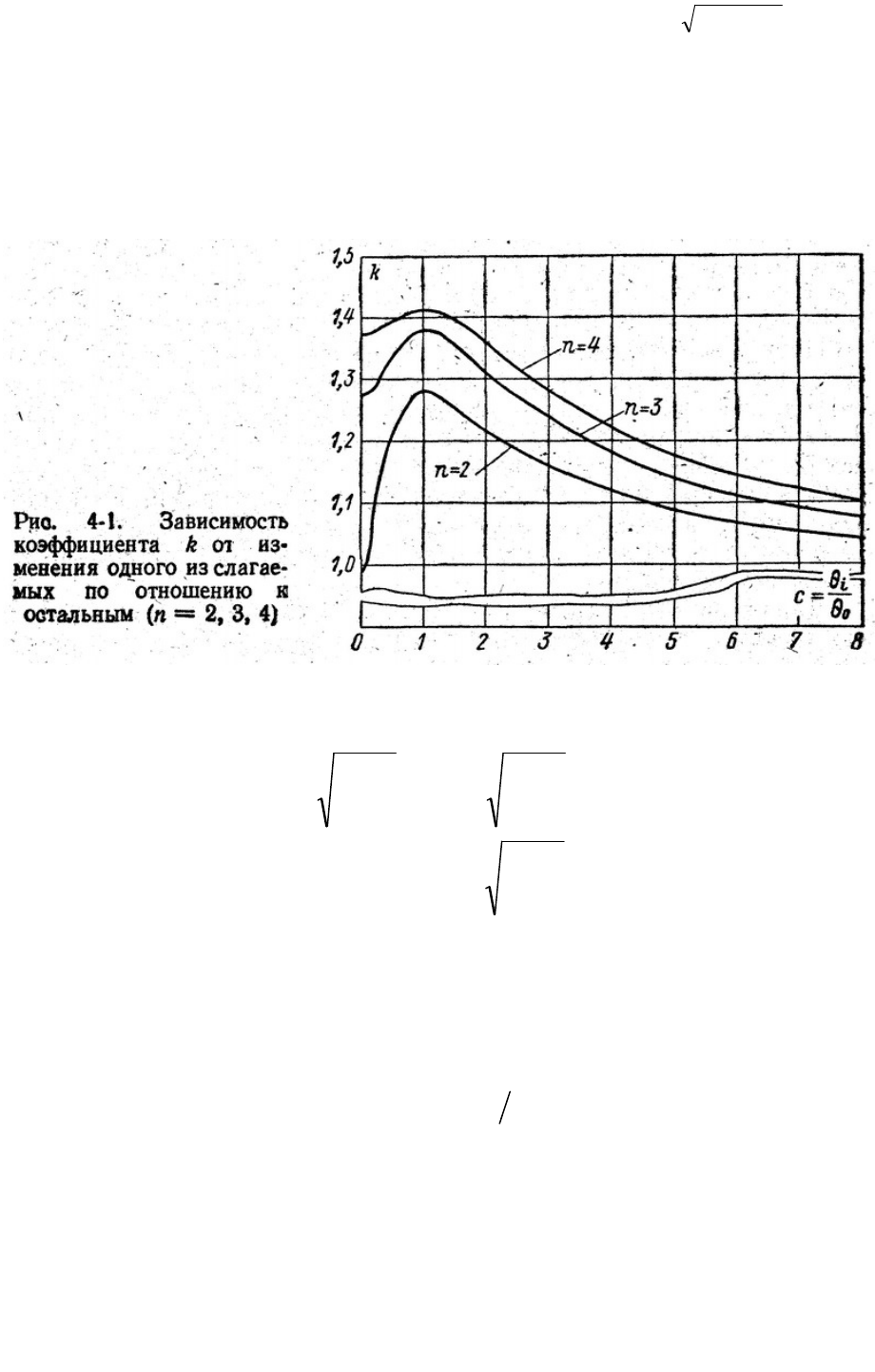
Зависимость k от отношения
0
θθ
i
с = для
99.0
=
α
приведена на рис. 4-1. .
При очень малом числе слагаемых, т. е. когда
32
÷
=
n
, может
оказаться, что вычисленное по формуле (4-3) значение
θ
Таблица 4
-
1
Значения коэффициента k в зависимости от числа
слагаемых и доверительной вероятности
Число
слагаемых
n
Значения коэффици
ента
k
при
доверительной вероятности
α
0,90
0,95
0,99
0,9973
2
0,97
1,10
1,27
1,34
3
0,96
1,12
1,37
1,50
4
*
1,12
1,41
1,58
5
*
*
1,42
1,61
6
*
*
*
1,64
…
…
…
…
…
∞
0,95
1,13
1,49
1,73
Примечание
. Для г
раф таблицы,
отмеченных звездочкой, коэффициент k не
вычисляется, так как
θ
при данном n выходит за
пределы крайнего интервала.
превышает арифметическую сумму
i
θ , что невозможно. Например, %2,0
1
=θ ,
%1,0
2
=θ , по формуле (4-3) при 99,0
=
α
получим %4,10,104,04,1 ≈+=θ .
Между тем %2,1
21
=+θθ , т. е. θθθ <+
21
.
Поскольку всегда должно выполняться условие
∑
=
≤
n
i
i
1
0θ , то при очень
малом числе слагаемых следует сравнить значение
θ
, найденное по формуле (4-
3), с арифметической суммой слагаемых и в качестве оценки границы
результирующей неисключенной
систематической погрешности принять то из них, которое меньше. Таким
образом, можно записать:
,
,
11
2
1
11
2
1
2
≥
<
=
∑∑∑
∑∑∑
===
===
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
kесли
kеслиk
θθθ
θθθ
θ
(4-5)
При большом числе слагаемых результирующая погрешность имеет
практически нормальное распределение. Оценку дисперсии этого распределения
2
ϑ
S найти нетрудно, так как согласно известной теореме она равна сумме
дисперсий слагаемых:
∑
=
=
n
i
i
S
1
22
3θ
ϑ
(4-6)
Задавшись доверительной вероятностью
α
, получим
θ
как границу
доверительного интервала:
ϑα
θ Sz=
(4-7)
где
α
z — квантиль нормированного нормального распределения, отвечающая
выбранной доверительной вероятности
α
.

Применение формулы (4-7) вместо (4-3) оправдано при большом
числе слагаемых, когда это сопровождается повышением точности
получаемого результата. Однако, как следует из приведенной выше оценки
погрешности расчетов по формуле (4-3), точность не может быть повышена
более чем на 10% (при 99,0
=
α
). Вместе с тем формула (4-3) пригодна и для
суммирования малого числа слагаемых. Поэтому для практических
расчетов соотношение (4-3) представляется предпочтительным.
4-5. Суммирование элементарных
систематических погрешностей методом
перебора вариантов
Задача суммирования погрешностей в § 4-4 решена для случая, когда
слагаемые имеют равномерное распределение. Вообще же слагаемые
могут иметь и другие распределения.
В общем случае объединение случайных величин требует построения
композиции распределений слагаемых. Если функции распределений
заданы аналитически, то их композиция находится либо прямым
интегрированием произведений функций, либо с использованием
характеристических функций, что обычно упрощает решение [29].
Возможно и графическое решение задачи [21, 37].
Однако на практике аналитический вид функций распределения
обычно неизвестен. По опытным данным можно построить лишь
гистограмму, а переход от нее к функции распределения неизбежно связан
с погрешностью. Поэтому рассмотрим суммирование случайных величин,
распределение которых задано гистограммами, а не функциями
распределений [18].
Пусть требуется найти функцию распределения случайной величины
n
ξξξ ++= ...
1
, где
i
ξ — случайная величина, заданная гистограммой с
i
m
интервалами в области возможных ее значений с границами
i
a и
i
b .
Таким образом, интервал
[
]
i
imiiii
lllba +++= ...,
21
,
ni ,...,1
=
.
Вероятности попадания в каждый интервал гистограммы примем
равными площади той части гистограммы, которая принадлежит данному
интервалу (площади соответствующего столбца гистограммы):
{
}
ikiki
plP =∈ξ
,
где
i
mk ,...,1= — номер интервала гистограммы распределения случайной
величины
i
ξ .
На рис. 4-2 в качестве примера приведена гистограмма с пятью
интервалами равной длины
i
l , так что
iii
lab 5=− .
Для этой гистограммы
lWp
i 11
=
,
lWp
i 22
=
, …,
lWp
i 55
=
