Рабинович С.Г. Погрешности измерений

Подождите немного. Документ загружается.

Необходимое число наблюдений можно найти с помощью

приведенного в том же параграфе критерия. Для этого нужно сопоставить

(

)

zS и предел допускаемой погрешности образцового прибора

∆ :

()

≥

∆

Отсюда

( )

∆

−

≈

∑

Если для образцового прибора известна граница систематических

погрешностей

θ :

θϑ ≤

то в приведенные соотношения вместо

∆ следует подставить

θ .

Рассмотренный способ поверки удобен для анализа, но на практике его

избегают, так как отсчеты долей делений по шкале поверяемого прибора

трудно сделать достаточно точно. Однако результаты, приведенные для

этого способа поверки, являются, общими. В частности, они будут

справедливы и для основного способа поверки, при котором указатель

поверяемого прибора всякий раз устанавливают на контролируемую

отметку шкалы, а соответствующее действительное значение измеряемой

величины находят по показаниям образцового прибора.

Если поверка осуществляется с сокращенным числом измерений

благодаря плавному подходу с двух сторон к одной и той же отметке

шкалы поверяемого прибора, то оценку поправки находят на основе

среднего арифметического получаемых двух оценок погрешности.

Хотя поправку мы оценили путем усреднения показаний приборов, ее

затем можно вносить и в каждое отдельное показание. Это целесообразно,

если поправка существенна по сравнению с составляющими погрешности

прибора. Заметим, что если поправка найдена на основе усреднения

показаний прибора, а прибор применяется с однократным отсчитыванием

показаний, но с внесением поправок, то случайные погрешности можно

считать имеющими

[

]

M ψ .

При наличии значительных случайных погрешностей иногда

желательно оценить дисперсию или среднее квадратическое отклонение

этой погрешности. Если поверка осуществляется путем измерения

неизменной величины одновременно поверяемым и образцовым

приборами, то справедливо уравнение (10-4) и очевидно, что

()

( )

−

∑

и формально трудностей в решении вопроса нет; однако трудно получить

достаточно точные отсчеты

x .

Если же при каждом наблюдении указатель поверяемого прибора

устанавливать на одну и ту же отметку шкалы, то из эксперимента мы не

получим данных для решения задачи. В этом случае согласно (10-1)

iПi

yA −=ζ

(10-6)

причем constA

= . Следовательно,

[

]

[

]

yDD =ζ

и получаемая в соответствии с этим отношением оценка дисперсии зависит

как от интересующей нас случайной погрешности поверяемого прибора,

так и от случайной погрешности образцового прибора. Чтобы решить

задачу, нужно иметь оценку среднего квадратического отклонения

образцового прибора

(

)

yS .

Теоретически, т. е. отвлекаясь от погрешности отсчитывания

показаний поверяемого прибора, оба рассматриваемых способа поверки

можем считать эквивалентными. Возьмем случай, когда к обоим приборам

подведена одна и та же величина с истинным значением

. При этом

−

yxA , и, следовательно,

−

Отсюда с учетом соотношений (10-2) и (10-4) получаем

ζ ,

где

iii

yxz −= .

Следовательно, для показаний, получаемых в соответствии с формулой

(10-6), имеем

[

]

[

]

[

]

[

]

iiii

yDxDyDD +==

ζ .

Соответственно этому

(

)

(

)

(

)

ySxSyS

22'2

+= .

Зная

(

)

и имея на основе экспериментальных данных

(

)

yS находим

(

)

(

)

(

)

ySySxS

2'22

−= .

(10-7)

Соотношение (10-7) говорит о желательности знать среднее квадратическое отклонение

для образцовых средств измерений. Однако средства измерений, для которых известны средние

квадратические отклонения и, например, пределы погрешности определения поправок, трудно

применять для поверки средств измерений, рассчитанных на применение с однократным

отсчитыванием показаний. В таких случаях для образцовых средств измерений было бы полезно

кроме названных выше характеристик знать и пределы суммарной погрешности. Для этого не

требуется отдельно определять и составляющие и пределы суммарной погрешности при каждой

поверке. По-видимому, связь между суммарной погрешностью и ее составляющими для каждого

типа средств измерений неизменна. Поэтому, если в процессе исследований, выполняемых,

например, при аттестации образцовых средств измерений, установить эту связь, то в

дальнейшем, при очередных поверках, достаточно определять только часть рассматриваемых

погрешностей.

10-3 Интерпретация результатов измерений

при поверке и пути снижения брака поверки

Выше рассмотрены вопросы нахождения оценок погрешностей поверяемых

средств измерений. По этим данным нужно принять решение о пригодности или

непригодности их для дальнейшей эксплуатации. Для средств измерений,

градуируемых при поверке, это решение основывается на контроле изменения их

погрешностей за время между двумя поверками.

Неточность оценок погрешностей, определяемая в основном погрешностями

образцовых средств измерений, приводит к ошибкам, в результате которых часть

неисправных, т. е. недостаточно точных, средств измерений признается годными

для дальнейшего применения (брак поверки первого рода), а часть в

действительности годных признается негодными (брак поверки второго рода).

Естественное стремление уменьшить брак поверки привело к многочисленным

попыткам найти необходимое для этого соотношение между пределами

допускаемых погрешностей поверяемых и образцовых средств измерений. Путь

решения задачи таков.

Рассмотрим опять поверку, при которой одна и та же величина

одновременно измеряется и поверяемым и образцовым средствами измерений.

Как отмечалось, такая схема проще других для анализа, но это не отражается на

общности получаемых результатов. В соответствии с условиями эксперимента

имеем

−

yxA ,

где х, у — показания поверяемого и образцового приборов,

, —

погрешности поверяемого и образцового приборов.

Отсюда

−

yxz .

(10-8)

Нам требуется установить, что ∆≤ζ , где

∆

— предел допускаемой

погрешности поверяемого прибора. Из данных опыта мы можем найти

;

будем считать, что если ∆≤z , то поверяемый прибор годен, а если ∆>z ,

то негоден. Однако ясно, что такая тактика дает правильный результат

лишь при абсолютно точном образцовом приборе. Ограниченная точность

образцовых приборов приводит к браку поверки.

Считая, что известны функции плотности распределения

погрешностей поверяемых и образцовых приборов, Е. Ф. Долинский

получил соотношения для вероятностей брака поверки и провел анализ

рассматриваемой методики поверки [19]. Вероятность брака поверки

первого рода означает

{

}

∆>

∆≤−=

γζPp

брака поверки второго рода —

{

}

∆≤

∆>−=

γζPp

Если функции плотности распределений погрешностей поверяемых и

образцовых приборов

(

)

ζf и

(

)

γϕ известны, то вероятности

p и

p можно

вычислить.

Брак поверки первого рода возможен при ∆+>ζ , т. е. при

∆

−

. При этом ∆≤−γζ , т. е.

∆

≤

−

∆

−

≥

−

Отсюда

∆

≤

∆

−

. Следовательно,

() () () ()

∫ ∫∫ ∫

+∞

∆

∆+

∆−

∞−

∆+

∆−

























= ζγγϕζζγγϕζ

ddfddfp

Брак поверки второго рода возможен при ∆≤ζ , т. е. при

∆

≤

∆

−

≥

. При этом ∆>−γζ , т. е.

∆

−

∆

−

или

∆

−

∆

Отсюда

() () ()

∫ ∫∫

∆

∆−

+∞

∆+

∆−

∞−













+= ζγγϕγγϕζ

dddfp

Если известны функции плотности распределений и их параметры, то

можно вычислить соответствующие значения

p и

p и проследить их

зависимость от соотношений между пределами допускаемых погрешностей

образцовых и поверяемых приборов.

Если к этому присоединить экономические соображение, то, казалось бы,

можно задачу выбора упомянутого соотношения решить однозначно. В самом

деле, повышение точности образцовых средств измерений сопровождается

повышением стоимости поверки. Брак поверки тоже имеет определенную

стоимость. Следовательно, варьируя погрешность образцовых средств

измерений можно найти минимум потерь и этот вариант считать оптимальным.

Математические соотношения для решения задачи получить нетрудно.

Однако, к сожалению, в общем случае нельзя оценить потери от применения

приборов, погрешности которых выходят за установленные границы. Вообще

экономический эффект повышения точности измерений, часто очень

значительный, выразить в денежном выражении трудно. Поэтому для

обоснования выбора соотношения между пределами допускаемых

погрешностей образцовых и поверяемых средств измерений экономические

критерии удается использовать только в исключительных случаях.

Кроме того, как уже отмечалось выше, принципиальную проблему

составляет определение функций распределения погрешностей средств

измерений, и вообще правомерность применения

вероятностной модели для описания распределения основных погрешностей

совокупности средств измерений каждого типа представляется весьма

сомнительной. Одна из причин этого состоит в том, что погрешности средств

измерения изменяются с течением времени.

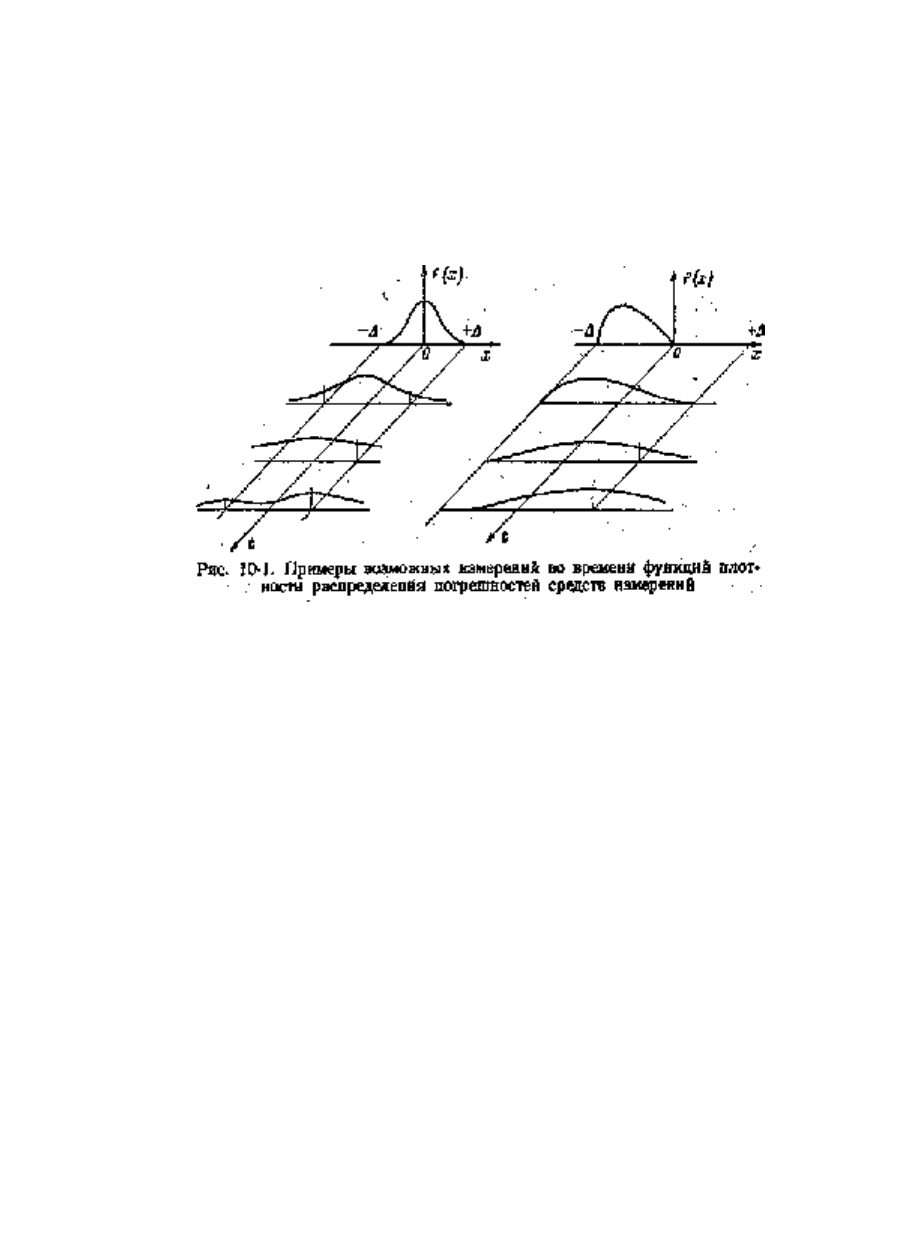
Пусть погрешности совокупности средств измерений какого-то типа в

момент выпуска их из производства имеют усеченное нормальное распределение с

нулевым средним. У мер: измерительных резисторов, шунтов, гирь и т. д. —

слишком большая погрешность какого-то одного знака приводит к

неисправимому браку. Это учитывают при изготовлении мер, и в результате

распределение основных погрешностей мер обычно оказывается

несимметричным. Гири, например, при выпуске из производства бракуются, если

их масса хоть сколько-нибудь меньше номинальной. Оба варианта

распределений представлены на рис. 10-1.

В процессе эксплуатации средств измерений их погрешности изменяются.

Обычно они лишь возрастают. В тех случаях, когда, как у гирь, заранее известно

направление изменения погрешностей и это учтено правилами их изготовления,

погрешности могут сначала уменьшаться, но затем они все же будут возрастать.

Соответственно изменениям погрешностей средств измерений деформируются

функции их распределений. Этот процесс, однако, протекает, не только

самопроизвольно. В моменты очередных поверок из применения изымаются те

средства измерений, погрешности которых выходят за установленные пределы.

Общая картина измерений функций плотности распределений во времени

примерно соответствует показанной на рис. 10-1. Процесс заканчивается в

конце концов тем, что рассматриваемые средства измерений прекращают свое

существование: либо их погрешности выходят за установленные пределы, либо

они приходят в негодность по другим признакам.

Действительная картина еще более сложна, так как парк средств

намерений каждого типа может периодически изменяться еще и за счет

поступления новых средств измерений.

Какое же распределение при рассмотренных условиях можно считать

правильно отражающим свойства средств измерений? Это неизвестно. Но

ясно, что распределения погрешностей средств измерений в момент выпуска их

из производства непригодны для описания свойств средств измерений,

находящихся в эксплуатации.

По существу, сказанное говорит о весьма возможной статистической

неустойчивости распределений основных погрешностей средств измерении.

Поэтому по одной партии приборов можно дать одну оценку для функции

распределений основных погрешностей приборов, по другой партии приборов

этого же типа — совершенно другую*

Нужно отметить, что такие свойства средств измерений, как функции и

коэффициенты влияния различных влияющих величин, как правило, не

изменяются со временем и поэтому для их описания с помощью

вероятностной модели есть гораздо большие основания.

Изложенные соображения говорят о том, что к расчетам вероятностей

брака поверки следует подходить очень осторожно. Конечно, возможен расчет

для наихудшего случая. Но возникает вопрос, какое распределение считать

наихудшим.

Тем не менее представляет интерес анализ чисто абстрактных ситуаций,

просмотр ряда моделей с целью выяснения общих закономерностей. Такой

анализ был проделан рядом авторов.

Предполагая нормальными распределения погрешностей и образцовых и

поверяемых приборов, Е. Ф. Долинский получил следующие результаты [19,

20]:

брак поверки зависит главным образом от соотношения между пределом

допускаемых погрешностей поверяемых приборов и средним квадратическим

отклонением погрешностей этих приборов; с уменьшением среднего

квадратического отклонения брак поверки уменьшается;

соотношение между погрешностями поверяемых и образцовых приборов

(между допускаемыми пределами этих погрешностей или между средними

квадратическими отклонениями этих погрешностей) влияет на брак поверки

гораздо меньше, чем свойства распределения погрешностей поверяемых

приборов.

В работе [45] построены зависимости брака поверки первого и второго

рода для случая, когда погрешности поверяемых приборов имеют нормальное

распределение, а погрешности образцовых

Выполненные в последние годы исследования подтвердили высказанные опасения и

показали, что распределения погрешностей средств измерений в общем случае нужно

считать неустойчивыми. Итоги этой работы опубликованы. Заключительной является статья

С. Г. Рабиновича и Т. Л. Яковлевой «Анализ устойчивости во времени распределений

погрешностей средств измерений» в журнале «Метрология», 1977, №7.

приборов — равномерное. В работе [54] получены аналогичные зависимости для

нормальных распределений погрешностей поверяемых и образцовых приборов,

для равномерных и для арксинусных распределений. Показано, что брак поверки

первого рода значительно снижается если при поверке сужать интервал для

допускаемых погрешностей поверяемых приборов по сравнению с

официально установленным. Подсчитано, что при отношении между пределами

допускаемых погрешностей образцовых и поверяемых приборов, равном 1:3,

вероятности брака поверки не превышают 0,035, если худшим случаем для

поверяемых приборов считать 1=∆ σ ; эта вероятность оценена как

удовлетворительная. При этом, однако, не учтено, что каждый прибор

поверяется не на одной, а на нескольких, обычно 3–10, отметках шкалы. Если

это учесть, то процент неправильно забракованных приборов будет не 3,5%, а

10–35% и процент неправильно признанных годными негодных в

действительности приборов также будет 10–35%. Такой процент брака поверки

нельзя признать удовлетворительным.

Отвлекаясь от статистической неустойчивости распределения погрешностей

поверяемых приборов, нужно отметить один принципиальный недостаток

данного подхода к характеристике качества поверки. Предположим, что мы

имеем функцию распределения погрешностей поверяемых средств измерений,

т. е. имеем погрешности всей их совокупности. Однако для каждой конкретной

партии приборов брак поверки будет зависеть от того, как много в этой партии

негодных приборов. Следовательно, вероятность брака поверки нельзя считать

удачным показателем эффективности поверки, так как такой показатель не

должен зависеть от того, много или мало плохих приборов поступает в

поверку.

С целью исключить влияние свойств поверяемых приборов на оценку

эффективности поверки было предложено использовать так называемые

оперативные кривые [27]. Оперативные кривые позволяют сравнивать между

собой случаи поверки, выполняемые с разными по точности образцовыми

приборами. Однако, чтобы оценить вероятность брака поверки, вновь нужно

иметь функции распределений погрешностей поверяемых приборов.

Если бы в поверку приборы поступали партиями, то можно было бы

говорить о функциях распределений для каждой партии и соответственно

этому — о браке поверки каждой партии, а затем о средних браках поверки.

Но в поверку приборы поступают и по отдельности, и небольшими партиями

(по несколько штук), так что при таком подходе о функциях распределений

говорить не приходится.

Возникшее противоречие можно разрешить, если обратиться к

некоторым, условно худшим распределениям. Для получения оценки

наибольшей вероятности брака поверки первого рода можно, например, взять

распределение погрешностей плохих приборов, т. е. приборов с погрешностью,

превышающей допускаемые

пределы. Поскольку на практике в поверку поступают не только плохие

приборы, то ясно, что в действительности вероятность брака поверки первого

рода будет всегда меньше полученного таким образом значения.

Аналогично для оценки верхнего уровня вероятности брака поверки

второго рода можно взять какое-то распределение погрешностей, не выходящее

за пределы допускаемых погрешностей.

При таком решении задачи возникает проблема выбора вида наихудших

распределений. Объективно этот вопрос решить нельзя, а вариантов можно

предложить очень много. Например, в качестве таких испытательных

распределений можно взять: для «плохих» приборов — симметричное

распределение, составленное из разнесенных на

∆

положительной и

отрицательной ветвей нормального распределения со средним квадратическим

отклонением ∆=

σ ; для «хороших» приборов — равномерное распределение в

пределах

∆

Распределение погрешностей образцовых приборов из осторожности

следует принять за равномерное, для которого заданы допускаемые пределы

∆± .

Однако обосновать данное предложение нельзя, и поэтому на нём

нельзя настаивать.

Таким образом, при рассмотренном и широко распространенном способе

поверки не удается найти достаточно убедительного метода для обоснованного

выбора соотношения между погрешностями образцовых и поверяемых средств

измерений. Поэтому на практике этот вопрос решают волевым путем, путем

стандартизации критического соотношения между пределами допускаемых

погрешностей. Так, в электроизмерительной технике принято, что

погрешность образцовых приборов должна быть не менее чем в 5 раз меньше

предела допускаемой погрешности поверяемых. В стандартах на электронные

приборы требования к точности образцовых средств измерений более мягкие:

указанное отношение обычно равно 3. Другие соотношения (например, 1:10)

встречаются редко.

Соотношения 1:10 и 1:5 обычно не вызывают возражений, но часто их

технически трудно обеспечить. Соотношение же 1:3 постоянно вызывает

критику, как недостаточное. Косвенным подтверждением недостаточности

этого соотношения является то, что для электронных приборов

предусмотрено при выпуске из производства сокращение пределов допускаемых

погрешностей приборов на 20%. Однако при очередных поверках таким

сужением интервалов допускаемых погрешностей не пользуются, и,

следовательно, только из-за погрешностей образцовых средств измерений

возможно признание в качестве годных таких средств измерений:, погрешности

которых на 30% превышают установленные для них пределы.

Нельзя ли выбрать другое правило выделения негодных приборов, чтобы

избежать трудностей, связанных с вероятностным обоснованием выбора

соотношения между погрешностями образцовых и поверяемых приборов? В

принципе данную задачу можно решить следующим путем.

Как следует из определения, годным прибором является прибор, для

которого ∆≤− Ax , и негодным, если ∆>− Ax .

Аналогичные неравенства справедливы и для

образцового прибора:

∆≤− Ay , если он годен, и

∆>− Ay , если негоден.

При

для годного прибора

∆

≤

−

. Но

∆+≤≤∆− yAy . Поэтому, заменяя

на

∆−y ,

получим для годного прибора

∆−∆≤− yx

(10-9)

Аналогично при

можно получить для

годного прибора

(

)

∆−∆−≥− yx

(10-10)

Повторяя выкладки для негодного прибора,

нетрудно получить соответствующие неравенства

∆+∆>− yx

(10-11)

(

)

∆+∆−<− yx

(10-12)

Представим рассмотренные соотношения на графике (рис. 10-2). С осью

абсцисс совместим шкалу поверяемого прибора. На оси ординат отметим точки

∆

−

, а около каждой из них — точки, отстоящие на

∆+ и

∆− . Если

∆

∆ остаются одними и теми же для всей шкалы прибора, то от отмеченных точек

на оси ординат проведем прямые, параллельные оси абсцисс.

Неравенствам (10-9) и (10-10) отвечает область

.Средства измерений, для

которых разности

−

попадут в эту область, безусловно годные независимо от

того, в каком отношении находятся погрешности образцового и поверяемого

прибора.

Неравенствам (10-11) и (10-12) отвечают области

III

. Средства

измерений, для которых разности

−

попадут в область

или

III

безусловно негодные.

Часть поверяемых средств измерений может иметь такие погрешности, что

∆+∆<−<∆−∆ yx .

Этим погрешностям отвечают области IV и V на рис. 10-2. Такие

средства измерений, по существу, нельзя ни забраковать,