Рабинович С.Г. Погрешности измерений

Подождите немного. Документ загружается.

Остальные сочетания дают

кij

yy > ,что означает невозможность получить недопустимо

большую погрешность.

При 0<

θ , 0<

мi

θ и

∆ получим

55,0 и 0,45

45,0

4,06,0

−

кк

yyy .

Отсюда находим вероятности забраковать приборы для каждого сочетания составляющих:

.050,05,018,055,0

,041,05,015,055,0

,018,05,005,073,0

=⋅⋅=

⋅

Следовательно,

.059,0

,05,0

122111

=++=

pppp

Вероятность изготовления качественного прибора

(

)

.89,0059,0050,01

=+−=

Аналогичные вычисления для °=∆ 8,0

дают:

.11,0 и 0,89

45,0

4,08,0

,11,0 и 0,89

45,0

4,08,0

,47,0 и 0,53

75,0

4,08,0

−

кк

yyy

.010,05,018,011,0

,008,05,015,011,0

,012,05,005,047,0

=⋅⋅=

⋅

Теперь 010,0=

p и 020,0=

p , а 97,0

p .

Средняя взвешенная вероятность изготовления прибора с погрешностью, меньшей

заданного предела, равна

.95,097,07,089,03,07,03,0

=⋅+⋅=+=

ГГГ

ppp

Следовательно, при приведенных выше свойствах блоков приборов и качестве

изготовления шкал примерно 95% приборов будут иметь приведенную погрешность, не

превышающую 1%.

Данный расчет выполнен для нормальных условий и определяет пределы основной

погрешности приборов.

При заданном пределе погрешности приборов получаемый процент брака может служить

основанием для повышения требований к качеству тех или иных

блоков, к усовершенствованию технологии их изготовления и т. п. Однозначное расчетное

определение, пределов допускаемых погрешностей всех блоков возможно при условии

назначения весовых коэффициентов их погрешностей. Объективно эти коэффициенты

определить, по-видимому, трудно, а порой и невозможно. Поэтому основным следует считать

путь оценки процента брака и такой подбор требований к блокам, при котором получаемый

процент брака можно признать допустимым.

9-6. Замечаний о расчете погрешностей

измерительных систем

Измерительные системы обладают той особенностью, что в

процессе эксплуатации их основную погрешность экспериментальным

путем оценить не представляется возможным. Объясняется это тем,

что измерительные системы представляют собой сложные устройства,

различные блоки которых пространственно разобщены и поставить их

в одинаковые условия без демонтажа и транспортировки в одно место

нельзя. Такие операции, однако, сложны и, что еще более важно,

делают систему на некоторое время неработоспособной. Поэтому для

измерительных систем основная погрешность становится нормой

погрешности, по которой осуществляется контроль качества

измерительных систем при их выпуске из производства. Именно в

таком смысле трактуется основная погрешность в ГОСТ 11323–65

«Устройства и аппаратура телемеханики. Общие технические

требования». Для измерительных систем, которые создаются на месте

применения как уникальные устройства, основную погрешность даже

при изготовлении не всегда можно экспериментально оценить для

системы в целом ввиду сложности необходимого испытательного

оборудования.

Отмеченная особенность измерительных систем объясняет то

большое внимание, которое в последние годы уделяется расчетам

погрешностей измерительных систем. В монографии [57] приведен

перечень работ по расчету погрешностей измерительных систем*

Мы ограничимся некоторыми замечаниями о путях расчёта

погрешностей измерительных систем, которые представляются

перспективными.

Деление измерительных систем на однородные и неоднородные

связано с методами расчета их погрешностей. Однородные системы в

отношении оценивания основной погрешности ничем не отличаются

от многоблочного прибора. Так же как простые средства измерений,

их можно характеризовать дополнительными погрешностями,

возникающими при регламентированных значениях влияющих

величин, или функциями и коэффициентами влияния.

Дополнительно назовем статьи М. А. Земельмана, опубликованные в журнале

«Измерительная техника» за 1973 г., в №4 и 5 соответственно: «Об исходных

предпосылках расчета погрешностей измерительных информационных систем» и

«Методика расчета погрешности линейной измерительной информационной системы».

Поэтому погрешность измерительной системы в рабочих условиях можно

оценить тем же путем, что и погрешность измерительного прибора. Однако,

поскольку маловероятно, что для каждого случая применения

измерительной системы будут оцениваться и учитываться значения

влияющих величин (это слишком сложно), то погрешность системы в

рабочих условиях целесообразно оценивать методами, применяемыми для

оценивания погрешностей технических измерений. Суммирование

элементарных погрешностей нужно выполнять вероятностными методами.

В результате целесообразно получить доверительные границы,

погрешности измерений, выполняемых измерительной системой в рабочих

условиях.

Неоднородные измерительные системы отличаются от однородных

методами расчета погрешностей. Исходной формулой, связывающей

погрешности измерительной системы с погрешностями блоков и помехами,

остается все та же формула (9-5):

∑ ∑

= =

jjii

zWVy

1 1

εζ .

Коэффициенты влияний определяются по уравнению связи выходного

сигнала системы со свойствами блоков и помехами и в большинстве

случаев не зависят от условий измерений.

Например, при измерении мощности в соответствии с формулой

путем измерения сопротивления резистора R и силы тока

, как

нетрудно увидеть, коэффициенты влияния относительных изменений

сопротивления и силы тока соответственно равны 1=

V и 2=

V и не зависят

от условий измерении.

Будем считать, что от условий измерений зависят только параметры

блоков. Изменения параметров блоков будем представлять как их

погрешности.

Относительную погрешность блока i в рабочих условиях представим

суммой его погрешности в нормальных условиях

ε и погрешностей,

вызванных влияющими величинами:

∑

ikii

εεε

(9-22)

где

ε — погрешность блока

, вызванная отклонением влияющей величины

с номером k (k=1,...,N) от ее нормального значения.

Погрешности блоков

ε могут иметь и систематическую и случайную

составляющие. Погрешности, обусловленные устойчивыми изменениями

влияющих величин, — это погрешности систематические. Флуктуации

влияющих величин создают случайные погрешности.

С учетом формулы (9-22) приведенная выше формула (9-5) примет вид

∑ ∑∑∑

= ===

++=

iki

zWVyVy

1 111

εεζ ,

где

z — помеха в рабочих условиях.

Новым в данном выражении является средний член, представляющий

собой результирующую погрешность от всех дополнительных

погрешностей всех блоков.

Каждая дополнительная погрешность

ε обусловливается как

свойствами блока

, так и значением соответствующей влияющей

величины, вернее, его отклонением от нормального значения.

Мы хотим оценить возможную погрешность системы в условиях, при

которых возможны различные значения влияющих величин, причем

последние могут комбинироваться случайным образом. Функции влияний

могут быть разными у разных блоков. Поэтому для системы, свойства

блоков которой индивидуально не определяются (не контролируются), в

условиях, когда влияющие величины могут изменяться случайным образом,

при суммировании погрешностей, вызванных дополнительными

погрешностями блоков, их следует рассматривать как случайные величины.

Но для этого нужно иметь функции распределения. А их можно было бы

найти, имея функции распределений влияющих величин и

соответствующих свойств блоков системы. Этими сведениями мы, как

правило, не располагаем.

Известны попытки экспериментально найти функции распределения

некоторых величин [39]. Однако неизвестно, чтобы полученные данные

проверялись на устойчивость. Нам представляется, что в подавляющем

большинстве случаев они неустойчивы, и поэтому по экспериментальным

данным нельзя найти функцию распределения вероятностей влияющей

величины. В таком случае для того, чтобы влияющую величину

рассматривать как случайную, нужно произвольно выбрать для нее такую

функцию распределения, чтобы соответствующее ей изменение влияющей

величины было более значительным, чем то, что можно встретить в

действительности. Обычно специалист может хотя бы в виде гистограммы с

несколькими интервалами дать такую оценку функции распределения

вероятностей каждой из влияющих величин. Для свойств блоков есть более

определенные данные. Всегда известны либо пределы допускаемых

значений коэффициентов влияния, либо функции влияния и допускаемые

отклонения от них. Как всегда, когда заданы границы распределения, его

целесообразно считать равномерным. В отдельных случаях, однако, бывает

известно и само распределение.

По названным данным можно, найти функции распределения каждой

дополнительной погрешности. Затем уже рассмотренными методами нужно

построить композицию функций распределений, случайных величин,

которая дает функцию распределения

погрешности измерений, выполняемых системой, и позволяет оценить

доверительную погрешность измерения.

Таким образом, специфическим моментом рассмотренного решения

является построение распределения каждой из дополнительных

погрешностей.

Для иллюстрации метода решения этой задачи рассмотрим построение

распределения дополнительной температурной погрешности некоторого

блока. Пусть температурный коэффициент блока задан как предел

допускаемой дополнительной погрешности при изменении температуры на

10°С и известно, что эта погрешность пропорциональна изменению

температуры, но может быть как положительной, так и отрицательной. На

основе этих данных на рис. 9-8 построен график зависимости границ

дополнительной температурной погрешности блока от температуры. Справа

на этом же рисунке приведена гистограмма распределений температурных

коэффициентов блоков, которую в принципе можно получить путем

исследования ряда блоков.

Примем, что распределение отклонений температуры блока от

нормальной

t на основе опыта специалистов описано с помощью

гистограммы, приведенной на рис. 9-9.

Пользуясь этими данными, построим функцию распределения

температурной погрешности блока. Прежде всего по крайним значениям

диапазона изменения влияющей величины

t и

t находим минимальную

θ и

максимальную

θ дополнительные погрешности блока:

{

}

0=≤

нt

P θθ ,

{

}

1=≤

вt

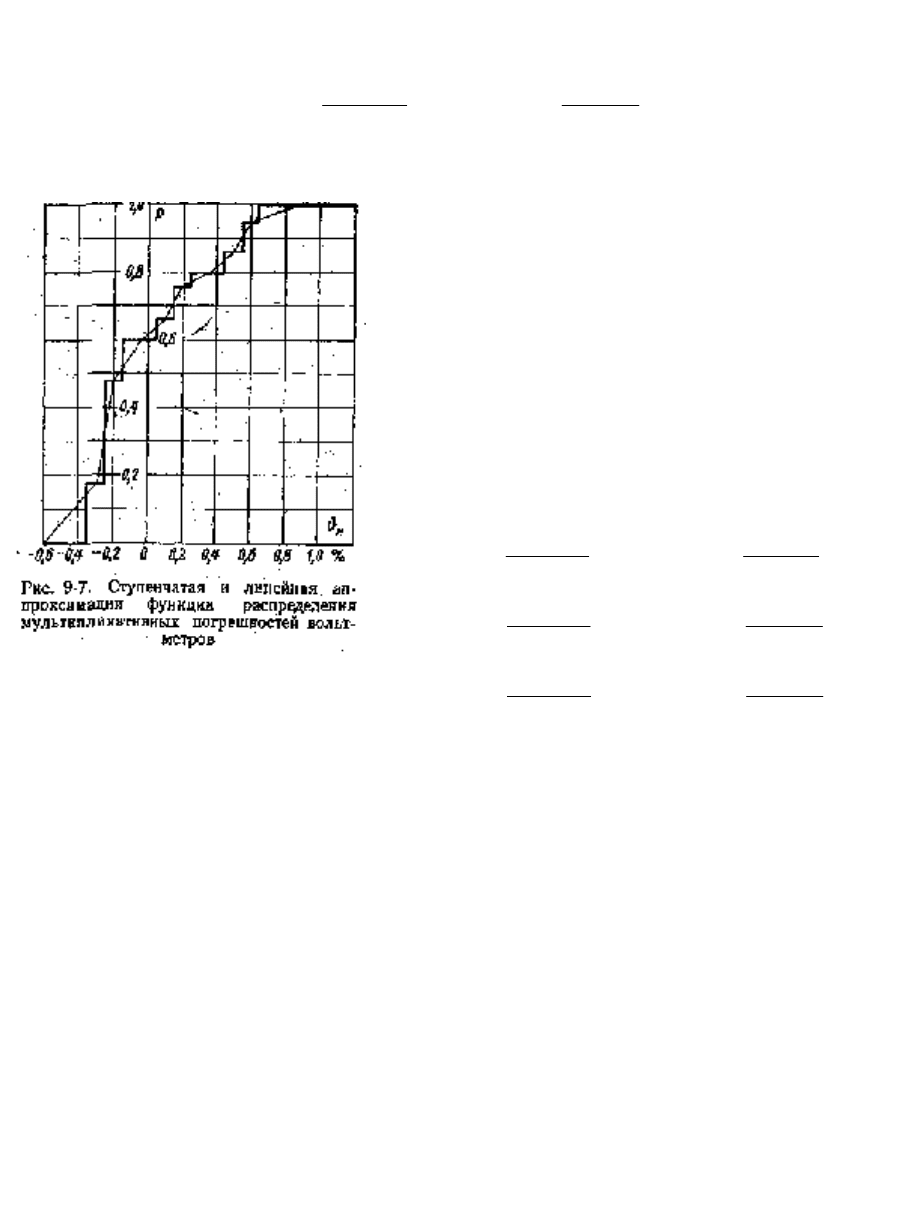
P θθ . Далее, если распределения величин даны как плавные функции

и мы хотим воспользоваться методом перебора (см. § 4-5), то надо заменить

их ступенчато изменяющимися функциями. От ступенчатой аппроксимации

затем переходим к дискретному распределению. Для этого каждому

интервалу значений влияющей величины поставим в соответствие среднее

значение величины на этом интервале. Для распределения температуры,

приведенного на рис. 9-9, будем иметь

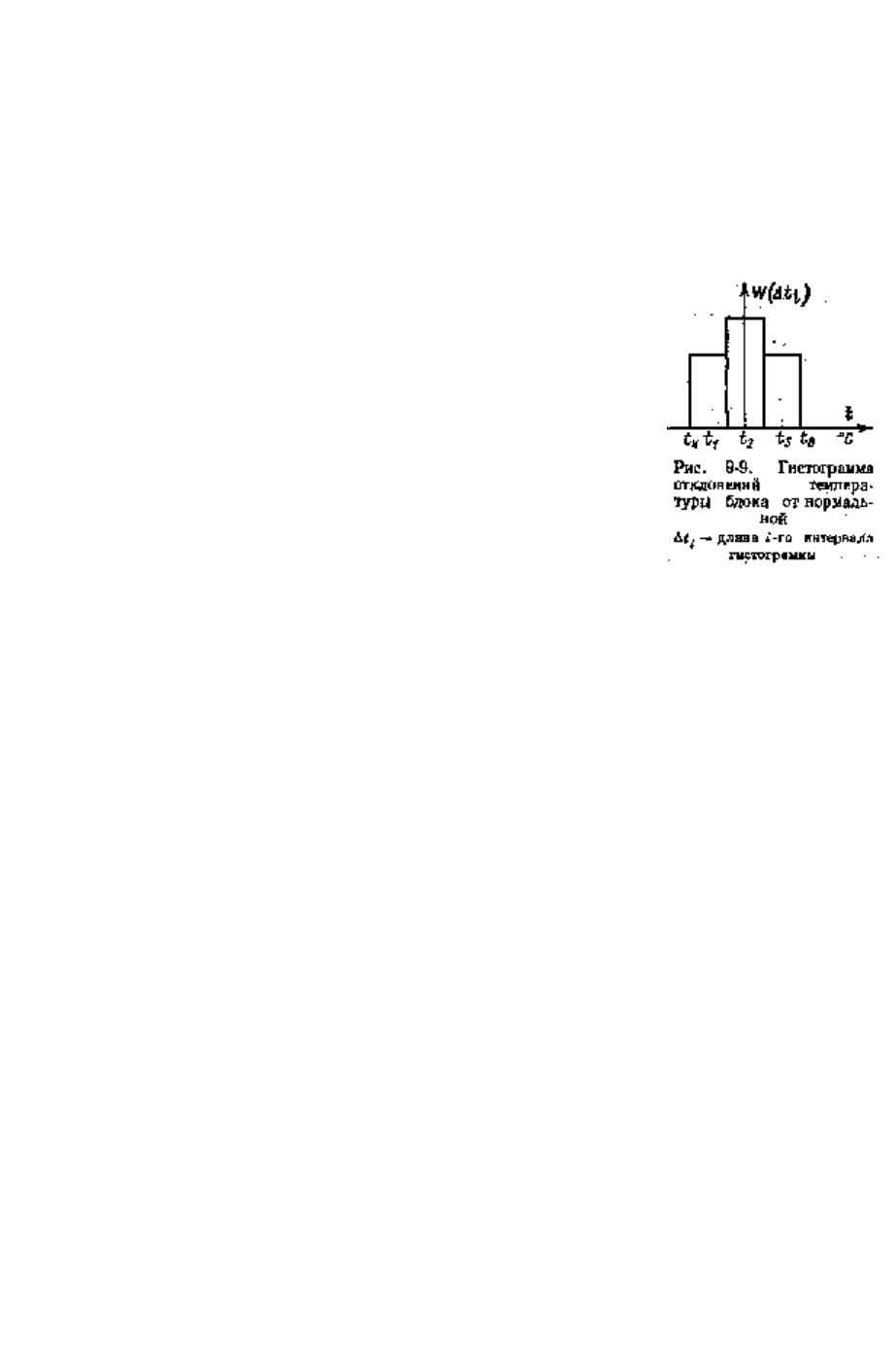
321

,, ttt . Вероятности, отвечающие каждой из этих величин,

321

ttt

ppp равны

площадям соответствующих столбцов гистограммы.

Для температурной погрешности аналогичное построение дает средние

температурные коэффициенты и отвечающие им вероятности

4321

,,,

QQQQ

pppp .

На графике 9-8 по этим средним температурным коэффициентам

4321

,,, QQQQ

проведены соответствующие им линии средних (для интервалов)

температурных погрешностей.

Теперь для каждой температуры

321

,, ttt получаем отвечающие им

температурные погрешности: для

t это ,

1111

tQ=θ ,

1212

tQ=θ ,

1313

tQ=θ и

1414

tQ=θ и т.д. Вероятность каждого значения

температурной погрешности равна произведению

вероятностей, отвечающих данному значению

температурного коэффициента и данному значению

температуры. Так,

{

}

{ }

...............................

1414

1212

1111

ppP

θθ

Поскольку 1

∑

p и 1

∑

p , то при каждой температуре

t сумма

вероятностей появления всех возможных температурных погрешностей

есть

p . Например,

{ }

114131211

ttQtQtQtQ

pppppppppp =+++==

∑

θθ

так как

4321

=+++

QQQQ

pppp

Соединим все полученные значения температурной погрешности в одну

совокупность. Получим набор реализаций температурной погрешности и

вероятности появления каждой из них. Как видно из изложенного, эта

совокупность значений представляет собой полную группу событий. По

этим значениям и отвечающим им вероятностям нетрудно построить

сначала ступенчатую, а затем и сглаженную кривые, представляющие собой

приближения к искомой функции распределения.

Однако с учетом того, что для расчета были взяты наихудшие функции

распределений влияющих величин, полученная в итоге функция

распределения погрешностей будет давать приуменьшенные вероятности.

Например, если некоторому интервалу в соответствии с этой функцией

распределения отвечает вероятность 0,95, то в действительности этой

погрешности отвечает большая вероятность.

ГЛАВА ДЕСЯТАЯ

ВОПРОСЫ ТЕОРИИ ПОВЕРОЧНЫХ ИЗМЕРЕНИЙ

10-1. Виды поверок

Необходимой предпосылкой единства измерений является

единообразие средств измерений. Это означает, что все средства измерений

должны быть носителями допущенных к применению единиц, а их

погрешности не должны выходить за предусмотренные, заранее известные

границы. Для достижения этих целей все средства измерений, находящиеся

в эксплуатации, подвергаются периодической поверке, при которой с

помощью образцовых средств измерений проверяют, не выходят ли

погрешности за допускаемые пределы.

При выпуске средств измерений из производства всегда

экспериментально определяют их погрешности. Расчеты погрешностей,

которым посвящена предыдущая глава, направлены на то, чтобы дать

возможность предвидеть точность проектируемых средств измерений.

Определение же погрешностей изготовленных средств измерений всегда

выполняется экспериментально, путем измерений.

При поверке не всегда устанавливают значения погрешностей средств

измерений, в большинстве случаев ограничиваются тем, что выявляют,

находятся ли они в заданных пределах. Таким образом, различают поверку

с установлением значений погрешностей поверяемых средств измерения,

т. е. поверку с нахождением поправок, и поверку, при которой

ограничиваются тем, что устанавливают, лежат ли погрешности средств

измерений в заданных для них границах.

Кроме того, различают поверку комплектную и поэлементную. При

комплектной поверке определяют погрешность поверяемого средства как

единого целого, при поэлементной — по погрешностям элементов

поверяемого средства измерений. Предпочтительной всегда является

комплектная поверка, обеспечивающая наиболее надежное решение задачи.

Однако в некоторых случаях комплектная поверка невозможна и

приходится обращаться к поэлементной.

При поэлементной поверке погрешность поверяемого средства

измерений вычисляется теми же методами, которые были рассмотрены в § 9-

2 для решения прямой задачи расчета погрешностей средств измерений по

погрешностям их блоков. Необходимые для расчета данные получают путем

измерений параметров блоков поверяемого средства измерений. Однако

обычно в полном объеме эта задача решается только один раз, и при этом

устанавливаются нормы на погрешности блоков. В дальнейшем при поверке

ведется лишь контроль параметров блоков и проверка работоспособности

средства измерений. Если параметры блоков удовлетворяют

установленным для них нормам, то и погрешность поверяемого таким

образом средства измерений находится в установленных пределах.

10-2. Оценивание погрешностей средств

измерений при поверке

Погрешность

средства измерений определяется формулой

,AA

−=ζ

где

A — показание поверяемого прибора, номинальное значение меры и

т. д.,

— истинное значение измеряемой величины, величины,

воспроизведенной поверяемой мерой, и т. д.

Истинное значение А всегда неизвестно. Если вместо него

использовать соответствующее показание образцового средства измерений

A (действительное значение измеряемой величины), то вместо

получим

ДП

AA −=ζ

(10-1)

Для того чтобы в качестве оценки погрешности

можно было принять

ζ , нужно, чтобы разность ζζ −

была мала. Погрешность образцового

средства измерений

АA

−=γ .

Поэтому

γζζ =−

(10-2)

Чаще всего о погрешности образцового средства измерений известно

лишь то, что она не превышает установленного для нее предела

∆ . Тогда и

∆≤− ζζ .

В относительной форме погрешность определения погрешности

, как

следует из выражения

ζζ

−

зависит от самой погрешности

и возрастает с ее уменьшением. В

качестве оценки этой относительной погрешности естественно принять

ζε ∆= .

При выборе образцовых средств измерений обычно ориентиром

служит предел допускаемых погрешностей поверяемых средств измерений

∆

. При этом говорят о соотношении

∆∆=

k .

Относительную погрешность определения погрешности можно выразить

через k:

∆

= k

(10-3)

Например, при 1,0

k погрешность

∆

≈

3,0

оценивается с

относительной погрешностью, достигающей 30%.

Если средства измерений достаточно стабильны, то оценки их

погрешностей, получаемые при поверке, можно затем использовать для

введения поправок.

Иногда кроме оценивания погрешностей при поверке заново определяют

функцию преобразования измерительного преобразователя или определяют,

какому значению измеряемой величины отвечают показания прибора,

фиксируемые по имеющейся шкале, т. е. заново градуируют средства

измерений. Для мер такую процедуру называют калибровкой. Погрешности

средств измерений после калибровки или поверки с градуировкой в пределе

могут быть равны погрешности образцового средства измерений. Этот метод

поверки целесообразен для высокостабильных средств измерений. Особенно

часто он применяется при поверке образцовых средств измерений.

Погрешности не требуется оценивать очень точно, но все же принято

считать, что погрешность оценивания погрешностей не должна превышать

30%. При большей погрешности с учетом нестабильности средств измерений,

получаемые оценки быстро теряют всякий смысл.

На практике часто принимают 3,0

k . При этом, как следует из

соотношения (10-3), с погрешностью, не превышающей 30%, можно оценить

лишь погрешности

∆

≈

Приведенные выше рассуждения интересно распространить на случай,

когда средства изменений имеют значительные случайные составляющие.

Случайные погрешности делают неоднозначными показания приборов и

затрудняют как их поверку, так и применение. Если, например, при поверке

показывающего прибора нужно только проверить, не превышают ли его

погрешности установленного для них предела, то приходится повторять

измерения несколько раз и выискивать наибольшие погрешности. В ряде

областей измерений удаётся плавно изменять величину, подаваемую на вход

прибора. В таких случаях для выявления наибольшей погрешности на каждой

контролируемой отметке шквалы часто достаточно выполнить всего два

измерения: одно — при приближении к отметке шкалы со стороны меньших,

второе — сo стороны больших показаний.

Иногда, несмотря на значительные случайные погрешности, все же

требуется найти поправку к показаниям поверяемого прибора. Эта поправка

представляет интерес, если она существенна по сравнению с другими

составляющими погрешности прибора.

Для решения задачи рассмотрим поверку, при которой одна и та же

величина одновременно измеряется образцовым и поверяемым приборами. Пусть

показания образцового прибора

, а поверяемого

. Разность показаний

приборов

−

(10-4)

В общем случае







++=

yiyi

xixi

ψϑ

(10-5)

где

ϑϑ , — систематические,

yixi

ψψ , — случайные погрешности приборов при

-м сличении.

Для случайных погрешностей приборов имеем

[

]

M ψ и

[

]

M ψ

Предположим, что для нахождения поправки усредняются показания

приборов. Используя соотношения (10-4) и (10-5), получим

111













+−+=

∑∑∑

===

nnn

Поправка

111













+−+−=−=

∑∑∑

===

nnn

Погрешность образцового прибора

ψϑγ += . Если известно, что

∆≤γ , то тем более

∆<+

∑

При достаточном числе наблюдений влияние случайных погрешностей

поверяемого прибора становится несущественным. Это значит, что

∑∑

Полагая малой и погрешность образцового прибора, получаем ответ:

zC −=

Полученная оценка найдена с погрешностью, не меньшей систематической

составляющей погрешности образцового прибора. Оценить эту погрешность

можно по методике, изложенной в § 5-1.