Рабинович С.Г. Погрешности измерений

Подождите немного. Документ загружается.

от устройства средств измерений. Поэтому расчеты этих метрологических

характеристик входят в задачи теории погрешностей средств измерений

конкретного принципа действия.

Погрешности средств измерений в рабочих условиях (т. е. при

отклонении влияющих величин от нормальных значений или при выходе их

за пределы областей нормальных значений) и их расчет по известным свойствам

средств измерений и условиям измерений рассмотрены как составная часть

задачи оценивание погрешностей измерений.

Таким образом, наиболее важной задачей общей теории погрешностей

средств измерений является задача расчета основной погрешности.

Нужно заметить, что изложенное полностью соответствует сложившейся

практике контроля качества средств измерений: проверяются свойства

собственно средств измерений, т. е. их основная и дополнительные

погрешности при заданных изменениях влияющих величин или коэффициенты

и функции влияния, а не погрешности в рабочих условиях, зависящие как от

свойств средств измерений, так и от значении влияющих величин. Задаче расчета

основной погрешности средств измерений по погрешностям образующих их

блоков посвящено много работ, но даже ее основные варианты еще нельзя

считать решенными. Тем не менее некоторые общие методы, необходимые для

оценивания погрешностей средств измерений, уже выработались. К ним в

первую очередь относится так называемый метод структурного анализа,

позволяющий приводить ко входу или к выходу прибора влияние любой из

помех или влияние изменения параметра любого из блоков прибора.

В разработке и обосновании метода структурного анализа большую роль

сыграли известные работы Н. Т. Бруевича [9, 10] и Д. А. Браславского [7]: Этот

метод теперь можно считать общеизвестным, и мы будем им пользоваться, не

останавливаясь на его описании.

Названную выше задачу оценивания результирующей погрешности можно

поставить применительно к отдельному прибору или совокупности приборов

определенного типа. В первом случае задача состоит в том, чтобы по известным

параметрам блоков конкретного прибора оценить погрешность этого прибора.

При этом можно либо найти погрешности (и поправки) прибора на определенных

отметках шкалы, либо оценить границы, в которых лежат погрешности данного

прибора. Эти задачи приходится решать при создании уникальных средств

измерений и при поэлементной поверке. Наиболее сложным вопросом при

этом является вопрос о той погрешности (как о характеристике

неопределенности), с какой находится погрешность рассматриваемого

средства измерений. Выясняется этот вопрос обычно методами, применяемыми

для обработки результатов наблюдений при косвенных измерениях.

Во втором случае, т. е. применительно к совокупности средств

измерений, задача ставится иначе. По свойствам блоков прибора нужно

оценить границы, в которых лежат погрешности приборов (прямая задача).

Но чаще заданными являются границы для погрешностей приборов и

требуется найти процент приборов, погрешность которых будет лежать в

этих границах (обратная задача). [42].

Каждую из названных задач, правда, с некоторыми модификациями

можно поставить для любого вида средств измерений: для мер,

измерительных преобразователей, измерительных приборов и

измерительных систем, если только их погрешности вызываются

отклонениями от номинальных значений параметров блоков, образующих

эти средства измерений.

9-2. Расчет погрешностей приборов

Рассмотрим последовательно обе задачи, т. е. прямую и обратную,

относящиеся к совокупностям средств измерений.

В общем виде информативный параметр сигнала на выходе прибора

связан с информативным параметром сигнала на входе

, параметрами

блоков прибора

(

)

ni ,...,1= , помехами и другими причинами аддитивных

погрешностей

(

)

mjz

,...,1= зависимостью

(

)

zxAfy ,,= .

(9-1)

Для каждого параметра установим номинальное значение, т. е.

значение, при котором средство измерений не имело бы погрешности.

Отклонения действительных свойств блоков от номинальных приводит к

образованию погрешности прибора. Назовем условно отклонения от

номинальных значений параметров блоков погрешностями блоков и

примем, что они выражены в форме относительных погрешностей

iiД

−

=ε ,

(9-2)

где

x — номинальное значение параметра блока,

iД

x — действительное

значение параметра блока.

Влияние погрешности каждого блока на погрешность прибора

определяется подобно тому, как это было рассмотрено в гл. 6 при

определении коэффициентов влияния погрешности измерения аргументов

на погрешность косвенного измерения.

Имея в виду относительные погрешности, можем написать

∂

⋅=∆

∂

⋅=

∆

Отсюда коэффициент влияния погрешности

x в относительной форме

будет

fyy

⋅

∂

∆

(9-3)

Коэффициенты влияния для причин аддитивных погрешностей,

поскольку последние нельзя представить как отклонения от каких-либо

номинальных значений, выразим в обычной форме

∂

(9-4)

В дальнейшем причины аддитивных погрешностей будем несколько

условно называть помехами.

Абсолютная погрешность прибора при показании у определяется

соотношением

∑∑

zWVy εζ

(9-5)

Уравнение (9-1) и коэффициенты влияния

V и

W находим, пользуясь

структурной схемой прибора. Получив же уравнение (9-5), мы можем

отвлечься от структурной схемы прибора и рассматривать лишь

составляющие погрешности. В уравнении (9-5) все они приведены к

выходу прибора.

Теперь рассмотрим подробнее прямую задачу, т. е. задачу оценивания

погрешностей приборов. Имеется в виду оценивание погрешностей

приборов в любой точке диапазона их показаний. Если известна точка, где

погрешность приборов максимальна, то в ряде случаев можно

ограничиться расчетом погрешности для этой точки. Часто такой точкой

является конечное значение шкалы прибора у

, так как при этом

максимальны мультипликативные составляющие погрешности.

Вычисления удобнее вести для относительных, а не абсолютных

погрешностей. При

yy = , относительная погрешность прибора, как

следует из формулы (9-5), будет

∑∑

iiк

Vεε

(9-6)

Дальнейшее решение зависит от того, какой информацией мы

располагаем о погрешностях блоков прибора и помехах. Случайные

погрешности блоков, вызываемые трением в опорах подвижных частей,

наводимыми э. д. с. и тому подобными причинами, будем рассматривать

как следствия влияния эквивалентных помех. Для этих

помех обычно

известны либо размах, либо наибольшее (без учета знака) значение, либо

среднее квадратическое отклонение.

Все погрешности, входящие в правую часть формулы (9-5) или (9-6),

разделим на систематические и случайные. Если

какой-либо член в формуле (9-5) имеет и систематическую и случайную

составляющие, то мы их разделим и в формуле (9-5) такой член заменим двумя

членами. При этом систематическими составляющими погрешностями считаются,

как всегда, погрешности, которые у каждого экземпляра прибора или у каждого

блока прибора имеют фиксированное значение.

Систематические, составляющие образуют систематическую, а

случайные — случайную погрешность прибора.

Случайная погрешность одного и того же прибора проявляется по-

разному при каждом применении прибора. Поэтому, если мы хотим оценить

наибольшую погрешность прибора, то должны к оценке границ его

систематической погрешности прибавить практически предельную случайную

погрешность.

Нужно заметить, что при теоретическом описании случайной погрешности

прибора ее рассматривают как случайную величину, причем чаще всего с

нормальным распределением вероятностей. Такая модель допускает возможность

любых по размеру погрешностей, и становится неясно, как на модели найти

предельную случайную погрешность прибора.

Примем за оценку предельной случайной погрешности прибора такое

значение случайной величины, что появление большей по модулю величины

можно считать пренебрежимо редким событием. Часто предельную случайную

погрешность принимают равной

(

— среднее квадратическое отклонение

показаний прибора при одном и том же значений измеряемой величины). При

известном

интервал с границами

отвечает доверительной вероятности

0,9973.

Нам это значение доверительной вероятности представляется слишком

большим, можно ограничиться значением 0,95.

Получаемую с помощью модели оценку предельной случайной

погрешности средства измерений будем называть практически предельной

случайной погрешностью.

Нужно обратить внимание на различие ситуаций при оценивании

погрешностей измерений и погрешностей средств измерений. В первом случае

мы имеем уже реализованные случайные погрешности и поэтому можем

суммировать случайные и систематические составляющие статистически. Во

втором случае мы оцениваем наибольшую погрешность прибора, которая может

проявиться в любом будущем опыте, и поэтому должны суммировать

составляющие арифметически.

Систематические погрешности совокупности однотипных блоков можно

рассматривать как набор реализаций случайной величины. Статистическое

описание последней дает, например, гистограмма. Для блоков с систематической

погрешностью нетрудно построить гистограмму распределения систематических

погрешностей. Для блоков кроме того со случайной погрешностью такое

описание усложняется, так как становится двумерным: реализация зависит как

от экземпляра блока, так и от того, какой в данном опыте окажется реализация

случайной погрешности этого блока. Но обычно вид распределения случайной

погрешности у всех однотипных блоков можно считать постоянным, так что

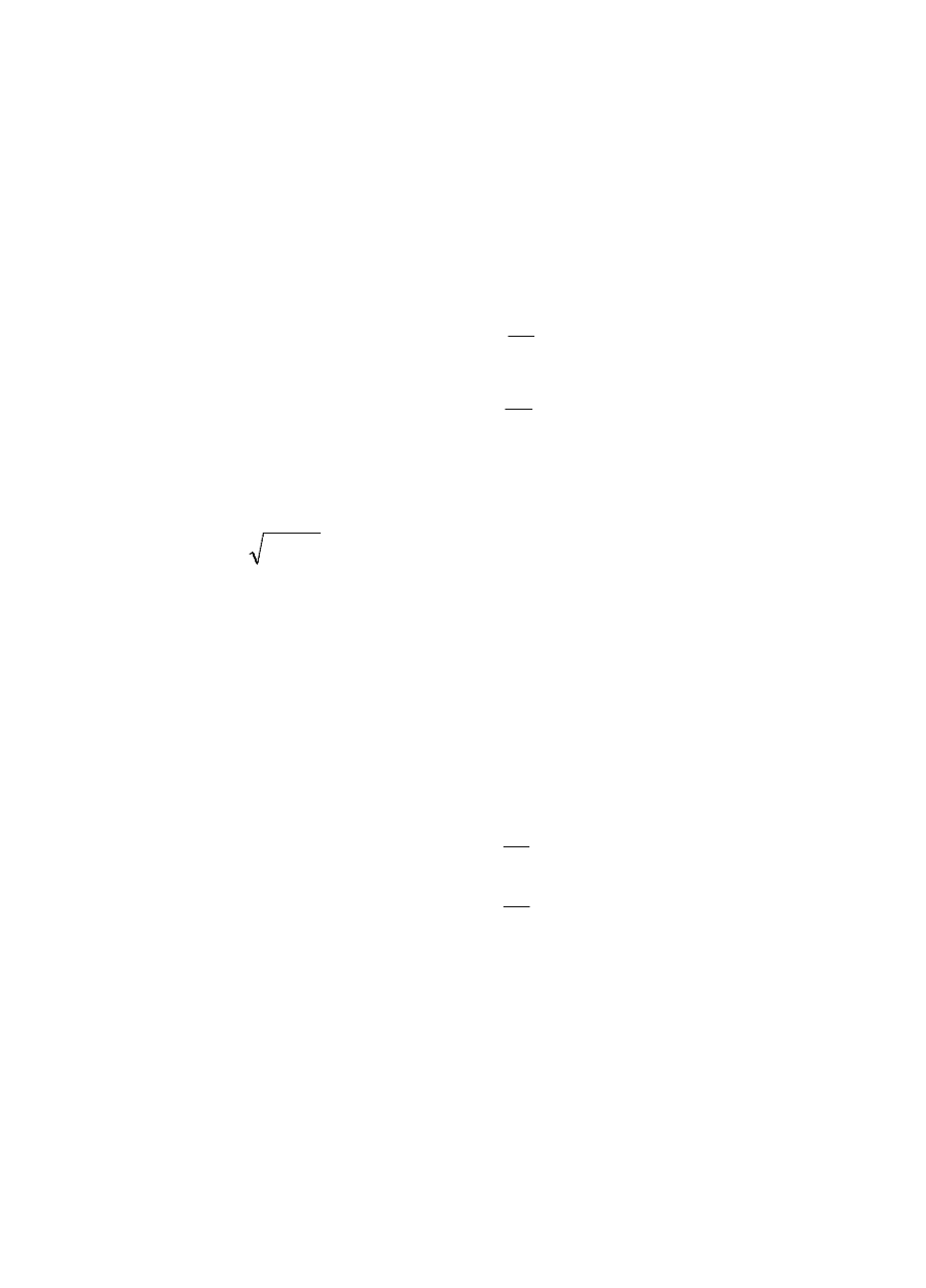
отличия их погрешностей определяются только, изменением какого-либо

параметра этого распределения. Это можно учесть и вместо двумерного

распределения случайной величины рассматривать одномерные распределения

соответствующего параметра и систематической погрешности блока.

Суммирование случайных величин связано с построением композиции их

функций распределений.

Если прибор состоит из большого числа блоков и слагаемых в формуле

(9-5) или (9-6) много, то композиция составляющих даст, как известно,

распределение, близкое к нормальному. Это позволяет упростить решение, так

как нетрудно найти параметры результирующего распределения:

[ ] []

[]

[] []

[]











∑∑

iiк

zDW

DVD

zMW

MVM

εε

(9-7)

В случае если некоторые погрешности взаимно связаны и

νλ

ρ —

коэффициент корреляции, то в выражение для дисперсии нужно ввести еще один

член, равный

λνλννλ

ρ DDVV2 .

Пользуясь оценками математических ожиданий составляющих и их

дисперсий, по приведенным соотношениям можно вычислить оценки

математического ожидания и дисперсии результирующего нормального

распределения. Прежде всего эта задача решается для систематических

погрешностей. Приняв процент приборов, погрешность которых должна быть

меньше вычисляемой оценки, за доверительную вероятность

, находим

отвечающие ей границы систематической погрешности:

[

]

(

)

[ ]

( )











−=

ккн

ккв

εσεθ

(9-8)

Затем оцениваем практически предельную случайную погрешность. Обычно

число слагаемых здесь очень невелико, и эта погрешность вообще не вычисляется,

а оценивается по экспериментальным данным. Если находим оценку среднего

квадратичеcкого отклонения результирующей случайной погрешности, то за

практически предельное значение принимаем

(

)

σψ

= , где

−

1q , а

находим по таблице распределения Стьюдента.

Затем в соответствии, со сказанным выше находим практически предельные

погрешности приборов:

. , ψθψθ −=∆+=∆

ннвв

(9-9)

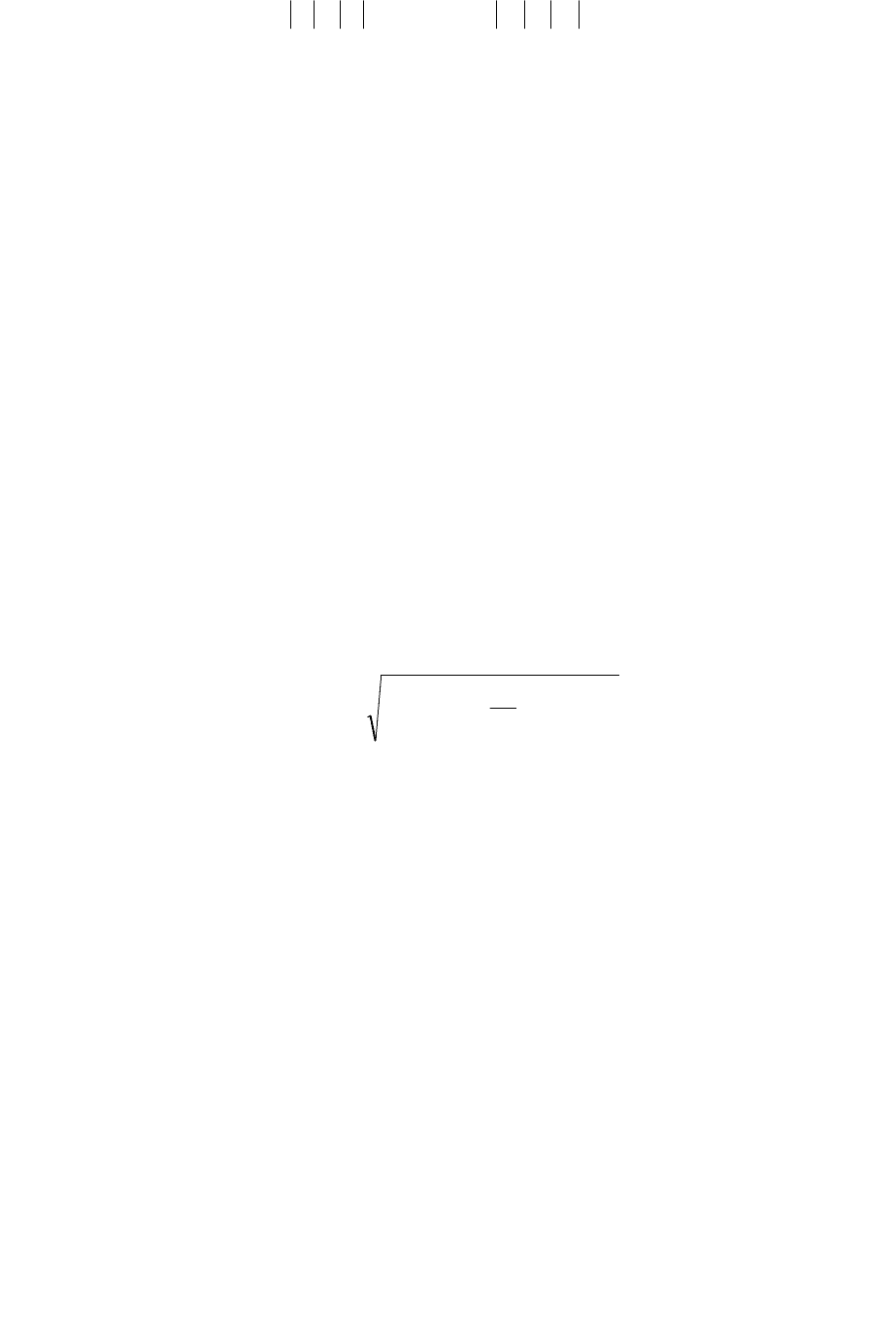
Обычно

[

]

M ε и

нв

θθ = , так что и

нв

∆=∆ .

При малом числе слагаемых нужно решать задачу путем построения

композиции распределений слагаемых. Однако из опыта можно получить лишь

гистограммы, а не функции распределений случайных величин. Переход к

функции распределения связан с аппроксимацией, и, как следствие, — с

соответствующей погрешностью. Между тем, как показано в гл. 4, композицию

распределений можно построить прямо по гистограммам слагаемых, пользуясь

методом перебора. При этом исключается аппроксимация гистограмм плавными

кривыми и связанная с этим погрешность. К тому же метод перебора связан с

простыми вычислениями, при необходимости легко осуществляемыми с

помощью ЦВМ.

Нужно отметить, что в общем случае вероятность, принимаемая для

вычисления границ систематической погрешности, может быть не равна

вероятности, отвечающей практически предельной случайной погрешности.

Следовала бы указывать обе эти вероятности (как это делается для

толерантных интервалов). Однако это сложно и не принято.

Если слагаемые заданы допускаемыми для них границами и нет данных в

пользу какого-либо распределения, то соответствующие погрешности

целесообразно считать имеющими равномерное распределение. В этом случае

доверительную границу систематической погрешности приборов можно найти по

несколько преобразованной формуле (6-9):

( )

∑∑

∆+=

Vk δθ

(9-10)

где k — коэффициент, значения которого приведены на стр. 96;

(

)

,...,1=δ —

пределы допускаемых систематических погрешностей блоков, образующих

мультипликативную составляющую погрешности прибора;

(

)

,...,1=∆ — то

же, но для погрешностей, образующих аддитивную погрешность прибора.

Практически предельная случайная погрешность

(

)

yψ находится так же,

как и в других случаях, и так же вычисляется суммарная погрешность приборов.

Поскольку систематические погрешности приборов рассматриваются как

случайные величины, то доверительная вероятность

, принятая для

вычисления границ систематической погрешности, означает долю приборов,

систематические погрешности которых не выходят за эти границы.

Часто погрешности блоков задают допускаемыми для них границами,

включающими как систематическую, так и случайную составляющие. В этом

случае можно поступить двояко. Основываясь на опыте, можно разделить

погрешность каждого блока на составляющие, после чего задача решается по

приведенной схеме. Но можно, не выделяя случайной погрешности,

рассматривать суммарные погрешности блоков как имеющие равномерные

распределения в заданных границах и складывать их статистически.

При отсутствии данных для разделения погрешностей на составляющие

второй способ представляется предпочтительным.

Вычисления погрешностей повторяются для ряда показаний прибора. При

этом нужно сохранять неизменными доверительные вероятности, одна из

которых была принята для определения границ систематической погрешности

совокупности приборов, а вторая — для определения их практически

предельной случайной погрешности. По полученным данным можно построить

график, показывающий, как меняется предельная погрешность приборов в

зависимости от их показаний. Погрешность может быть выражена в форме

абсолютных или относительных погрешностей, но чаще удобнее первые.

Перейдем ко второй задаче: задан предел допускаемой погрешности

приборов и требуется оценить вероятность встретить прибор с погрешностью,

меньшей этого предела.

Наметим общую схему решения. Вероятность

p встретить прибор с

погрешностью, выходящей за допускаемые границы, равна

(

)

нвГ

ppp +−=

(9-11)

где р

и р

— вероятности встретить прибор с погрешностью, выходящей за

верхнюю и нижнюю границу соответственно.

Можно написать, что

(

)

{

}

( ){ }

ψζ

−∆−≤=

−∆≥=

где

∆

— предел допускаемой погрешности приборов,

— практически

предельная случайная погрешность.

Для решения задачи нужно знать функцию распределения систематических

погрешностей приборов по совокупности.

Но практически предельную случайную погрешность не всегда можно

считать одной и той же для всех приборов, чаще она у них разная. Для более

точного решения задачи нужно найти распределение практически предельных

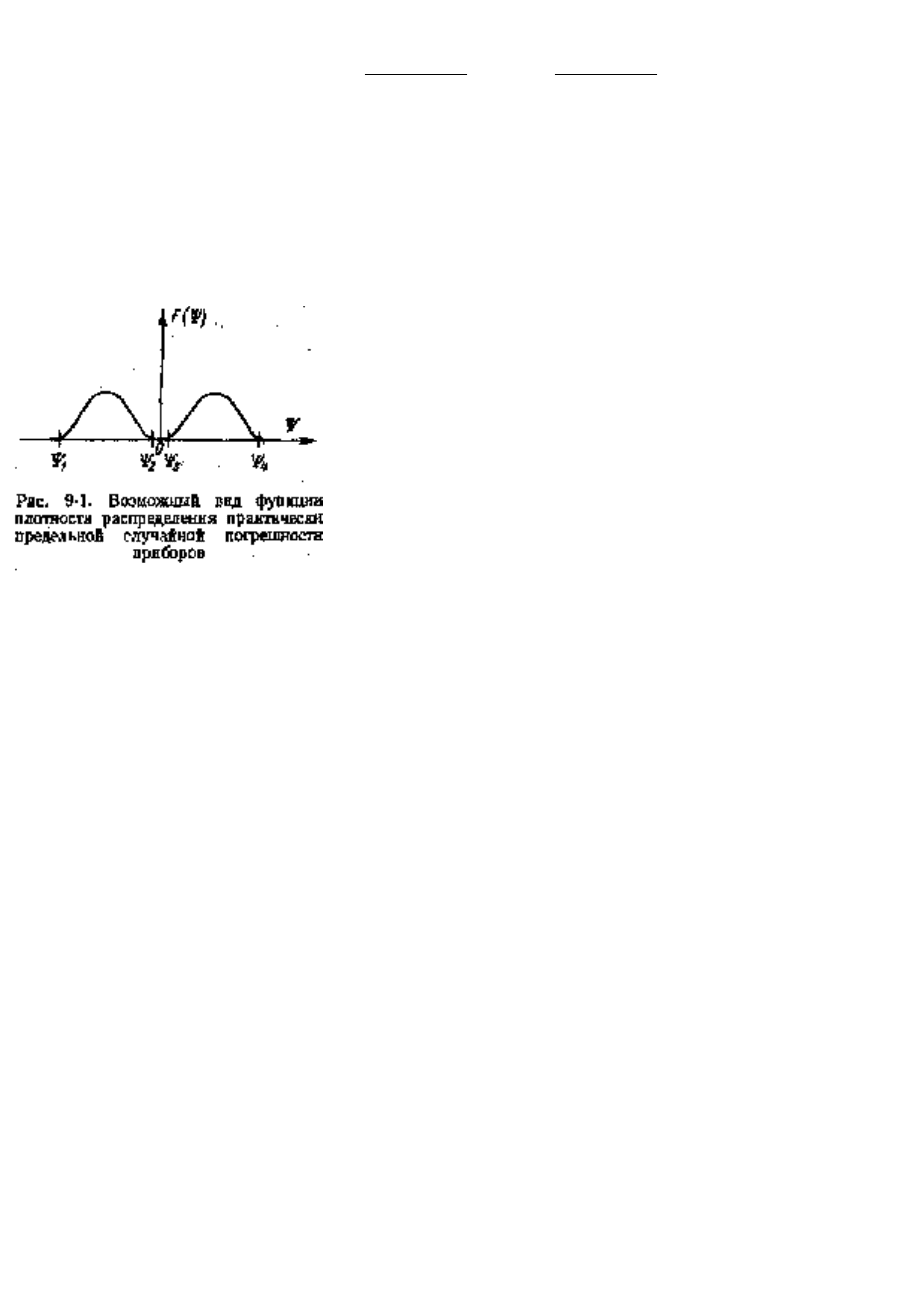
случайных погрешностей приборов. Пример возможной функции плотности

такого распределения приведен на рис. 9-1. Вероятности р

и р

теперь нужно

вычислять по формулам:

( ){ }()

∫

−∆>=

−∆−<=

ψψψζ

dfPKp

вв

нн

(9-12)

в которых значения функции плотности распределения

(

)

ψf играют роль

весовых коэффициентов, а К

и К

— нормирующие множители. Если функция

плотности распределения

(

)

ψf , как обычно

симметрична относительно оси ординат, то р

=р

и К

=К

=2. В общем же

случае

()

∫

ψψdf

()

∫

ψψdf

Введение коэффициентов К

и К

связано с тем, что по условию построения функции

распределения площадь под всей кривой плотности распределения равна единице, а нам нужно,

чтобы площадь под каждой ее ветвью (и при 0

, и при 0

) была равна единице.

Формулы (9-12) нетрудно получить, задавшись сначала несколькими значениями

процентом случаев, когда имеет место каждое из выбранных значений. Найдя р

для каждого

, естественно их сложить, взяв для каждого вес,

пропорциональный проценту «встречаемости». Отсюда,

экстраполируя к непрерывному распределению

приходим к формулам (9-12).

Таким образом, мы можем найти

вероятность изготовления средств измерений с

погрешностью, меньшей заданного предела,

если они имеют один единственный сигнал на

выходе. К таким средствам измерений

относятся, например, однозначные меры.

Однако гораздо чаще средства измерений имеют определенный

диапазон измерений. При этом вероятность встретить хороший прибор есть

вероятность того, что взятый прибор во всем диапазоне измерений будет

иметь погрешности, меньшие заданного предела. Как оценить эту

вероятность?

Казалось бы, применительно к показывающему прибору можно

вычислить вероятности

Гi

p для каждой отметки шкалы, прибора и,

перемножив их, найти

p . Однако так поступить нельзя, поскольку

погрешности в разных точках шкалы, в основном из-за мультипликативной

составляющей, не являются независимыми друг от друга. Кроме того, такие

расчеты были бы слишком трудоемки, так как шкала приборов часто имеет

100—150 отметок.

Рассмотрим другой путь решения задачи. Для определенности будем

иметь в виду показывающий прибор с одним диапазоном измерений.

Изложенная выше методика позволяет найти все составляющие

погрешности прибора на любой отметке его шкалы. Вычислим их для

конечного значения шкалы у

. Случайная составляющая обычно

незначительно меняется по шкале прибора. Поэтому, оценив практически

предельную случайную погрешность для конечного значения шкалы, мы

можем считать, что имеем ее для всей шкалы прибора.

Примем сначала, что все рассматриваемые приборы имеют по модулю

одну и ту же практически предельную случайную погрешность, равную

Систематические составляющие, прежде чем их суммировать, разделим

на аддитивные и мультипликативные составляющие и затем сложим их по

отдельности. Сложение выполняется статистическими методами. В

результате получаем функции плотности

распределений аддитивной и

мультипликативной составляющих для

yy = , т. е. для конечного значения шкалы.

Однако прибор может иметь

недопустимо большую погрешности на

любой отметке шкалы, и это надо учесть.

Систематическая погрешность

случайно взятого прибора в точке у шкалы,

складывается из мультипликативной

составляющей

мy

ϑ и аддитивной

ϑ :

ayмyy

ϑϑϑ += .

При этом

мyмy

θϑ ≤ ,

где

кммy

θθ = и

км.

θ — наибольшая мультипликативная составляющая

погрешности (без учета знака) при

yy = .

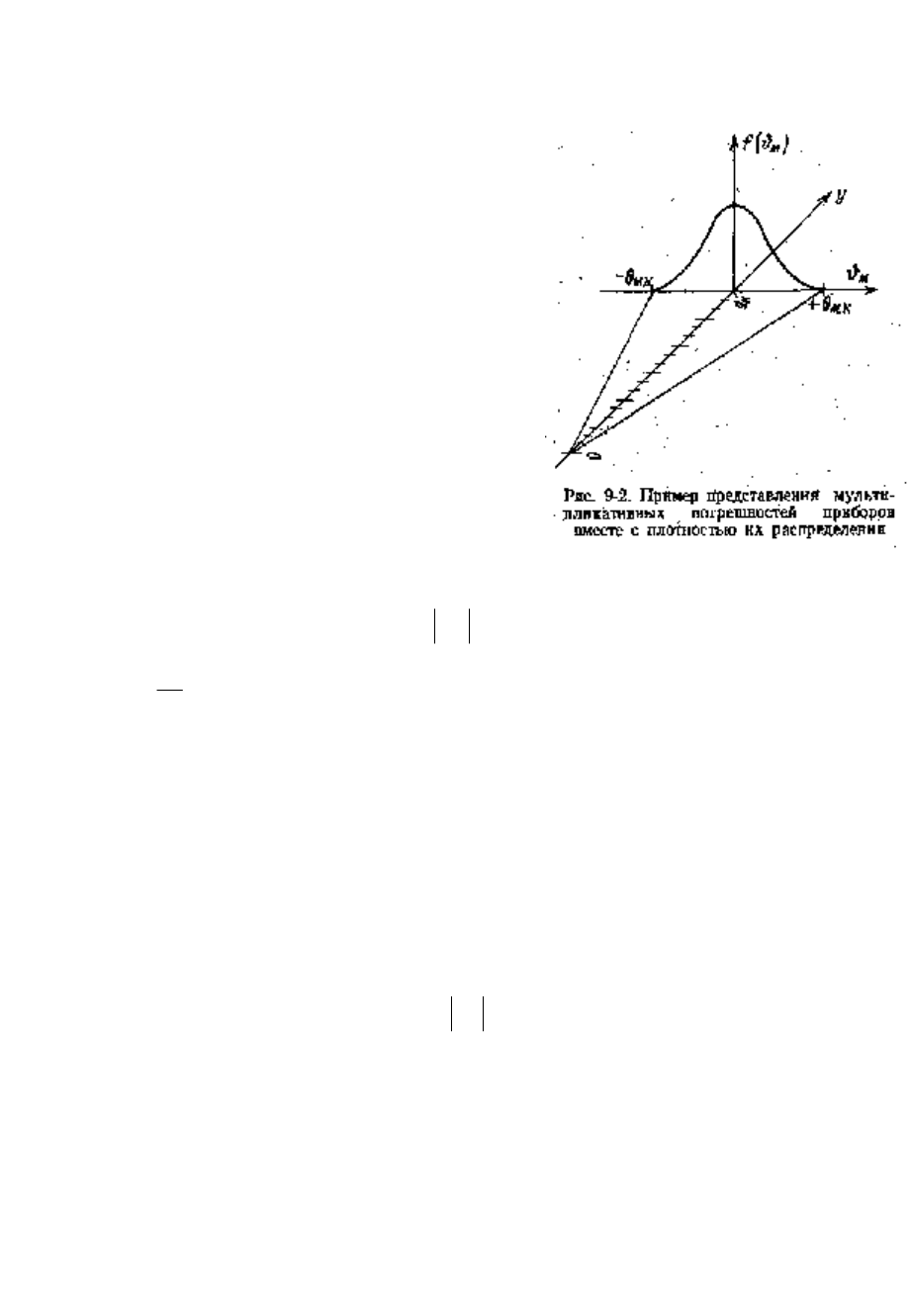
Пример изменения мультипликативных погрешностей прибора по

шкале вместе с функцией плотности распределения этой погрешности при

yy = приведен на рис. 9-2.

Напомним, что мультипликативная погрешность возрастает от начала

к концу шкалы пропорционально показаниям прибора. Поэтому ее можно

рассматривать как детерминированную величину.

Аддитивные же составляющие погрешности меняются вдоль шкалы

случайным образом, но так, что

ayay

θϑ ≤ , где

(

)

ϕθ = — наибольшая

аддитивная составляющая погрешности (без учета знака) в точке шкалы у.

Поэтому аддитивная составляющая должна рассматриваться как двумерная

случайная величина: она изменяется и в каждом сечении шкалы (на каждой

отметке шкалы) и вдоль шкалы.

Для нашей задачи целесообразно рассматривать не всю совокупность

аддитивных составляющих систематических погрешностей приборов, а

лишь совокупности наибольших и наименьших погрешностей, отобранных

по одной для каждого прибора.

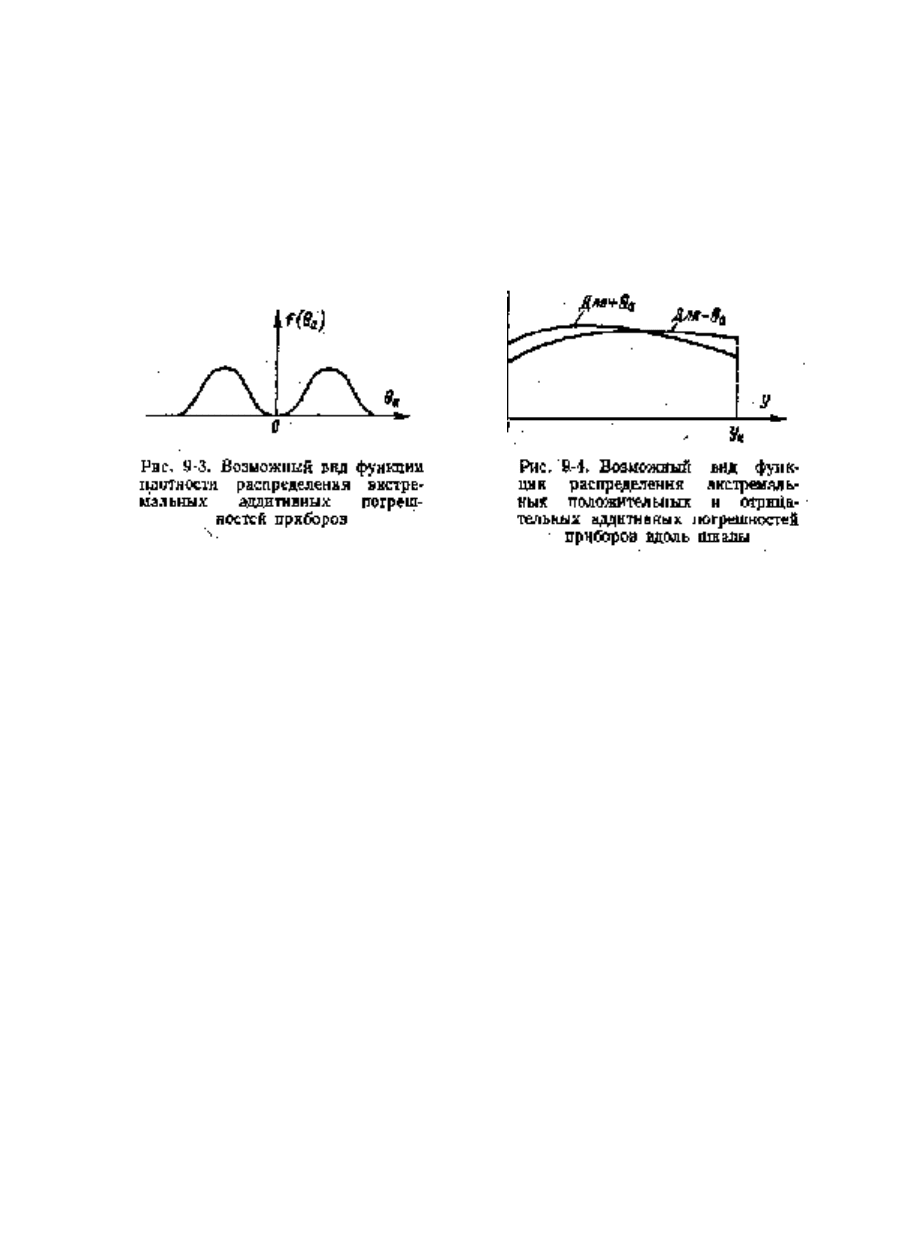
Статистически (по множеству приборов) эти экстремальные аддитивные

составляющие систематической погрешности

θ определяются двумя

функциями распределений, показанными на рис. 9-3 и 9-4.

График, приведенный на рис. 9-3, позволяет найти вероятность тех или

иных экстремальных значений

θ , а приведенный на рис. 9-4 — вероятность

встретить экстремальное значение (положительное или отрицательное) на том

или ином участке шкалы прибора.

Имея перечисленные зависимости, мы можем найти вероятность того,

что погрешность изготовленного прибора в любой точке его шкалы будет

меньше заранее заданного предела. Решение осуществляется численными

методами, а схема вычислений такова.

1. От непрерывных распределений

(

)

f ϑ и

(

)

f θ переходим к

дискретным. Для этого области возможных значений составляющих

[

]

кмкм ..

, θθ +− и

[

]

кака ..

, θθ +− делим на такое число интервалов, чтобы затем можно было каждый из

интервалов заменить средней на этом интервале погрешностью

(

)

мi

,...,1=θ и

(

)

,...,1=θ .

Вероятность появления каждой средней на интервале погрешности

принимаем равной площади под кривой плотности распределения

соответствующей погрешности на этом интервале.

Таким образом получаем ряд мультипликативных и ряд аддитивных

погрешностей и отвечающие им вероятности:

.,...,1 , ,

;,...,1 , ,

tjp

hip

aiaj

мiмi

Заметим, что мультипликативные погрешности

мi

θ отвечают

yy = , а

аддитивные

θ не связаны с каким-либо сечением шкалы.

2. Находим участки шкал, на которых возможно появление недопустимо

больших погрешностей.