Рабинович С.Г. Погрешности измерений
Подождите немного. Документ загружается.


Полученное неравенство показывает, что погрешность среднего
взвешенного, обусловленная погрешностью определения весов, во много раз
меньше последней. Сомножитель
x
xx
j
−
можно считать имеющим порядок
относительной погрешности слагаемых. Так, если эта погрешность имеет
порядок 0,01, то погрешность среднего взвешенного из-за погрешности
определения весов будет не менее чем в 100 раз меньше последней.
8-4. Объединение результатов измерений
с преобладающими случайными погрешностями
Рассмотрим вариант, возможный при статистических измерениях с
пренебрежимо малыми систематическими погрешностями. Каждый из
объединяемых результатов в этом случае обычно представляет собой среднее
арифметическое наблюдений, и различия между ними объясняются случайным
рассеиванием наблюдений в группах. Однако следует убедиться в том, что все
группы имеют одно и то же истинное значение измеряемой величины. Эта
задача решается методами, приведенными в гл. 3. Если нельзя считать, что во
всех случаях измеряется одна и та же величина, то объединение групп
лишено смысла.
Если объединение групп оправдано, то нужно проверить гипотезу о
равенстве дисперсий наблюдений в группах. Методы решения этой задачи
также приведены в гл. 3
В том случае, когда дисперсии групп можно считать равными, веса для
каждого из результатов вычисляются по формуле (8-7), совокупное среднее —
по формуле (8-1), а его дисперсию можно оценить по формуле (8-8).
Когда дисперсии групп нельзя признать равными, а сами дисперсии
неизвестны и неизвестны их отношения, то веса порой находят, подставляя в
формулу (8-4) вместо дисперсий их оценки. Дисперсию получаемого среднего
взвешенного оценивают, подставляя в формулу (8-5) оценки дисперсий
объединяемых значений, т. е. по формуле
()
( )
.
1
1
2
2
∑
=
=
L
k
k
k
xS
n
xS
Оценки дисперсий — случайные величины, получаемые на их основе
веса — тоже случайные величины, и хотя веса не требуется находить очень
точно, все же в этом случае среднее взвешенное приобретает несколько
условный характер. Однако при этом, как показано в работе [32], в случае
нормального распределения наблюдений среднее взвешенное остается
несмещенной оценкой измеряемой величины. Погрешность оценки среднего
квадратического отклонения, составляемой на основе приведенной формулы

для оценки дисперсии среднего взвешенного, уже при двух группах наблюдений
с числом наблюдений в каждой, большим девяти, не превышает 10%.
П р и м е р. Измеряется масса некоторого тела. В одном опыте получено
52,409
1
=m г как среднее арифметическое 15 наблюдений. Оценка дисперсии
группы наблюдений 1,0
2
1
=S г
2
. В другом опыте получено 44,409
~
2
=m г при
10
2
=n и 03,0
2
2
=S г
2
. Известно, что систематические погрешности измерений
пренебрежимо малы, а рассеивание наблюдений можно считать соответствующим
нормальному распределению. Нужно составить оценку массы тела с
использованием данных обоих опытов и оценить дисперсию результата.
Сначала выясним, оправдано ли объединение, т. е. нет ли недопустимого
различия между оценками измеряемой величины:
( )
;0067,0
15
1,0
1
2
1
1
2
===
n
S
xS
( )
;003,0
10
03,0
2
2
==xS
(
)
(
)
(
)
( )
.08,0
~~
;098,0
;0097,0
2121
21
2
2
1
2
21
2
=−=−
=−
=+=−
mmxx
xxS
xSxSxxS
Так как
(
)
2121
xxSxx −<− , то объединение возможно.
Проверим, можно ли считать, что обе группы наблюдений имеют одну
и ту же дисперсию. По формуле (3-27) находим
.3,303,0:1,0
2
2
2
1
=== SSF
Степени свободы 14
1
=k , 9
2
=k . Возьмем уровень значимости 2%. При
этом q=0,01 и 5=
q
F (см. табл. П-8), Так как F <F
q
, то можно считать, что
дисперсии групп равны.
Теперь найдем веса средних арифметических. Согласно (8-7) имеем
;6,025:15
1
==g 4,025:10
2
==g .
Вычислим среднее взвешенное: 49,40944,4094,052,4096,0 =⋅+⋅=m г.
Теперь найдем
(
)
mS . В соответствии с формулой (8-8) имеем
( )
(
)
( )
г. 103,5S и г 1028
05,01003,01503,091,014
2425
1
224
222
−−
⋅=⋅=
=⋅+⋅+⋅+⋅
⋅
=
m
mS
Если бы помимо оценки среднего квадратического отклонения нужно было
найти доверительную погрешность, то для того, чтобы воспользоваться
распределением Стьюдента, нужно по формуле (6-8) найти эффективное число
степеней свободы.

8-5. Объединение результатов измерений
при наличии и систематических и случайных
погрешностей
Предположим, что одна и та же величина А измеряется несколькими
способами. Каждый способ дал результат
(
)
Ljx
j
,...,1= с погрешностью
j
ζ :
jj
Ax ζ+= .
Для того чтобы можно было обоснованно объединить ряд значений х и
при этом получить более точную оценку измеряемой величины, необходимо
располагать определенной информацией о погрешностях
j
ζ . Будем исходить из
условия, что все рассматриваемые результаты измерений не имеют безусловно
постоянных систематических погрешностей. Однако это предположение
нуждается в проверке. Если его приходится отклонить, то поставленную задачу
решить нельзя.
Погрешность
j
ζ представляет собой сумму реализаций условно
постоянной систематической
j
ϑ и случайной
j
ψ погрешностей:
.
jjj
ψϑζ +=
Имея в виду возможное множество результатов при каждом способе
измерения, неизвестную систематическую погрешность
j
ϑ конкретной
реализации j-го способа измерения можно рассматривать как реализацию
случайной величины. Обычно для
j
ϑ оценивают ее границы
j
θ и считают их
симметричными относительно истинного значения измеряемой величины:
jj
θϑ ≤ ,
[
]
0=
j
M ϑ .
Случайную погрешность
j
ψ считают центрированной величиной, т. е.
[
]
0=
j
M ψ .
Таким образом, при отсутствии безусловно постоянных, например
методических, погрешностей можно написать
[
]
AxM
j
= .
Как следует из теории объединения результатов измерений, весовые
коэффициенты определяются дисперсиями этих результатов. В нашем случае
можно написать
[
]
[
]
[
]
jjj
DDxD ψϑ +=
(8-9)
Следовательно, если иметь дисперсии
[
]
j
Dϑ ,
[
]
j
Dψ , то задачу можно решить
строго и однозначно. К сожалению, сами дисперсии всегда неизвестны, и приходится
пользоваться их оценками. Чтобы составить оценки дисперсий совокупностей
систематических погрешностей для каждого способа измерения, кроме упомянутых
выше данных этих погрешностей, нужно знать вид их распределения. Как правило,
этого мы не знаем. Приходится прибегать к некоторым допущениям, например
считать их равномерными в оцененных границах. Хотя веса не требуется находить с
большой точностью, все же использование для их нахождения неконтролируемых
допущений вызывает некоторую неуверенность в том, что среднее взвешенное
является лучшей оценкой измеряемой

величины, чем объединяемые результаты. Именно, этим объясняется та
осторожность, с какой в метрологии относятся к объединению результатов
измерений.
В связи с отмеченным, прибегая к объединению результатов измерений,
всегда следует проверять, как согласуются исходные данные с полученным
результатом. Если обнаружится какое-либо противоречие, например совокупное
среднее окажется за пределами поля допуска какого-то слагаемого, то нужно
найти причину этого и устранить противоречие. Иногда это очень трудно,
приходится обращаться к специальным экспериментам.
Осторожность, с какой следует относиться к объединений результатов
измерений, обусловлена тем, что в данном случае сведения о погрешностях
используются для уточнения результата измерения, а не для характеристики его
неопределенности, как обычно.
Однако есть случаи, когда среднее взвешенное является естественной
оценкой измеряемой величины. Примером может служить точное измерение
активности
α
-излучающего источника*
10
. С целью повышения точности
активность измеряют при разных расстояниях от источника до детектора и при
разных диафрагмах. Сама измеряемая активность остается одной и той же.
Однако получаемые при разных диафрагмах ее оценки оказываются несколько
отличающимися одна от другой. Разные у них и погрешности. Поэтому, назначая
веса для полученных оценок измеряемой величины, в данном примере нужно в
соответствии с формулой (8-9) исходить из оценок дисперсий суммарной
погрешности объединяемых результатов измерений. Это, несомненно, приведет
к более правильному результату, чем если бы все результаты измерений считать
имеющими равные веса или назначать веса, учитывая только случайные
погрешности.
Итак, в рассматриваемом случае веса объединяемых результатов
измерений целесообразно вычислять по формуле
( ) ( )
( ) ( )
∑
=
+
+
=
L
k
kk
jj
i
SS
SS
g
1
22
22
1
1
ψϑ
ψϑ
где
(
)
j
S ϑ
2
,
(
)
k
S ϑ
2
—оценки дисперсий возможных множеств систематических
погрешностей j-го и k-го результатов измерений;
(
)
j
S ψ
2
,
(
)
k
S ψ
2
— оценки
дисперсий случайных погрешностей тех же результатов измерений.
10
Алексеев В. Я., Константинов А. А. Эталонная установка для воспроизведения
единицы
α
-излучающих нуклидов в диапазоне 10
4
—10
8
расп./с. — В кн. Исследования в
области измерения ионизирующих излучений. (Тр. метрологических институтов СССР). Л.:
ВНИИМ имени Д. И. Менделеева, 1973, вып. 145 (205), с. 5—20.

Теперь перейдем к оцениванию погрешностей совокупного среднего. При
решении этой задачи, учитывая малое значение погрешностей весов (см. § 8-3),
веса объединяемых результатов измерений будем считать точно известными
коэффициентами.
В случае статистических измерений для каждого результата
j
x можно
иметь оценку границ систематической погрешности
j
θ , и оценку среднего
квадратического отклонения
j
S случайной погрешности. Тогда
соответствующие показатели точности совокупного среднего будут
()
()
∑
∑
=
=
=
=
L
j
jj
L
j
jj
SgkxS
gkx
1
22
1
22
,θθ
На основе полученных оценок
(
)
xθ и
(
)
xS можно найти доверительные
границы суммарной погрешности совокупного среднего. Методика решения этой
задачи подробно рассмотрена в гл. 5.
При обыкновенных измерениях обычно известны только оценки границ
погрешностей объединяемых результатов измерений, т. е.
(
)
Lj
j
,...,1=∆ .
Основываясь на доступной информации о виде распределения возможного
множества фактических погрешностей каждого результата измерения, нужно
от границ погрешностей
j
∆ перейти к оценкам дисперсий этих погрешностей.
Получив последние, нетрудно найти веса объединяемых результатов измерений.
Затем по схеме, разработанной для линейных косвенных измерений (см.
гл. 6), можно вычислить доверительные границы погрешности взвешенного
среднего.
Остановимся на некоторых частных случаях обыкновенных измерений.
Рассмотрим измерение одной величины несколькими приборами.
Пусть случайные погрешности приборов малы по сравнению с пределом
допускаемых погрешностей, а последние у всех приборов одинаковы и равны
∆
.
Если показания приборов
n
xx ,...,
1
, а действительные их погрешности
(
)
∆<
iq
ϑϑϑ ,...,
1
, то можно написать:
.
..................
,
11
nn
xA
xA
ϑ
ϑ
−=
−
=
(8-10)
Естественной интуитивной оценкой истинного значения измеряемой
величины в случае ее измерения несколькими приборами равной точности
является среднее арифметическое их показаний
n
x
A
n
i
i
∑
=
=
1
~
.
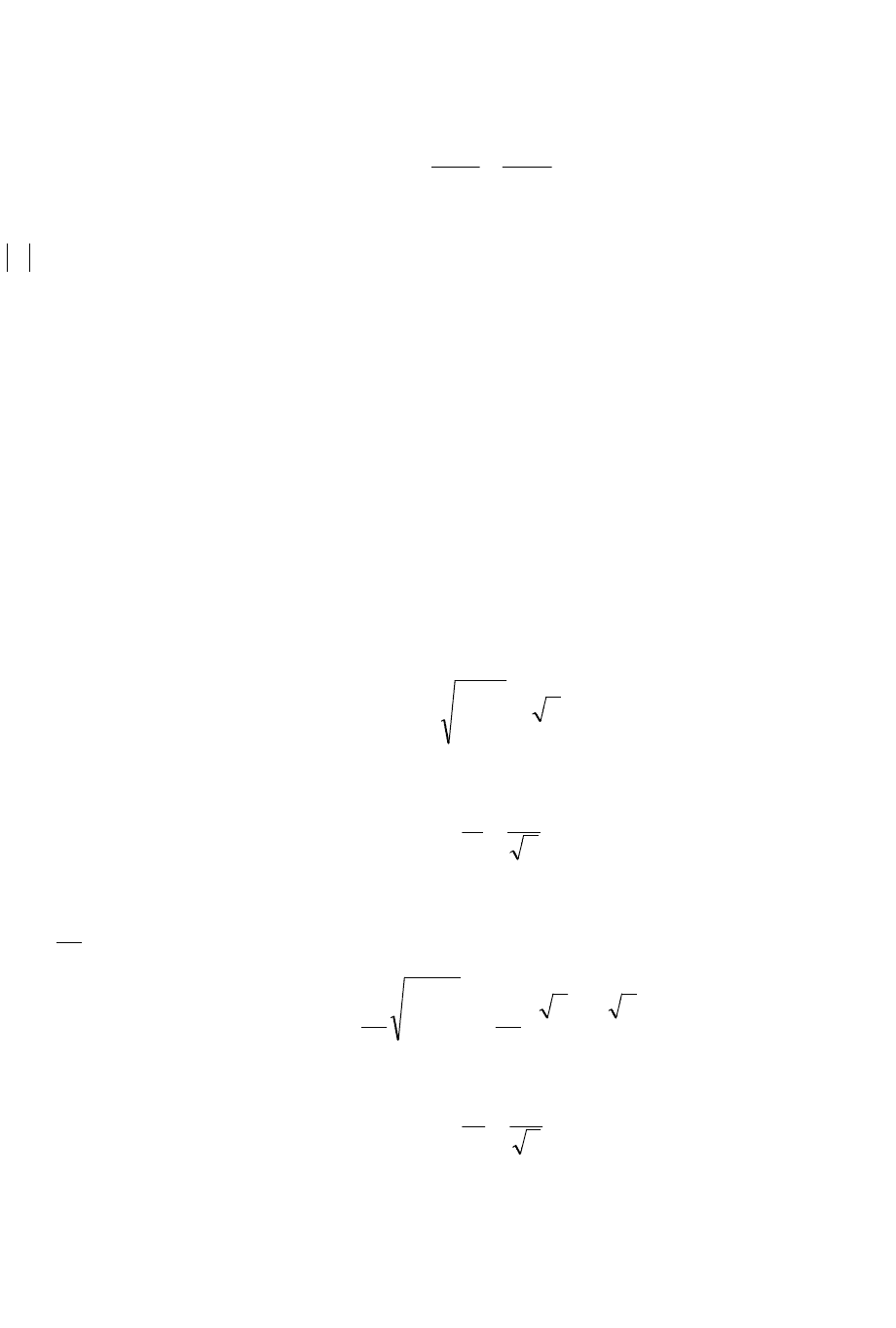
Математически доказано, что эта оценка является наилучшей в классе
оценок, линейно связанных с показаниями приборов [46, стр. 255].
Нам нужно оценить погрешность полученного результата. Сложив
левые и правые части уравнений (8-10) и разделив их на п, получим
n
n
x
A
n
i
i
n
i
i
∑∑
==
−=
11
ϑ
.
Реальные погрешности приборов нам неизвестны, мы знаем лишь, что
∆≤
i
ϑ для всех ni ,...,1
=
.
Чтобы найти границы суммы случайных величин
i
ϑ (а по совокупности
приборов данного типа их погрешности можно считать случайными
величинами), нужно знать их функции распределения. Как отмечалось
выше, эти функции по экспериментальным данным вряд ли можно найти.
Однако для сложных по устройству приборов часто можно считать
распределение их погрешностей симметричным. Математическое ожидание
распределения близко к погрешностям тех образцовых средств измерений,
с помощью которых эти приборы поверяют. В первом приближении
примем
[
]
0=
i
M ϑ .
Например, если погрешности приборов имеют равномерное
распределение, то согласно формуле (4-3) доверительная граница суммы
случайных величин равна
.
1
2
1
nkk
n
i
∆∆=
∑
=
θ
Отсюда доверительная погрешность оценки
A
~
будет
n
k
n
∆
==∆
∑
1
1
θ
.
Если распределение погрешностей приборов считать нормальным и
σ
α
2
1+
=∆ z , то
nnzz
n
i
i
∆===
+
=
+
∑
σσθ
αα
2
1
1
2
2
12
.
Тогда
n
n
∆
==∆
∑
2
2
θ
.
Эта оценка отвечает тому же уровню вероятности
α
, который был
принят при установлении предела допускаемой погрешности
∆
. Сравнение
∑
∆
1
и
∑
∆
2
показывает, что они отличаются лишь множителем
k
, который в
зависимости от доверительной вероятности
может колебаться от 1,1
(
)
95,0=α до 1,4
(
)
99,0=α . Основную роль, как и
следовало ожидать, играет число приборов. Чтобы получить уменьшение
погрешности в 2—3 раза, число приборов должно быть 5—10. Дальнейшее
увеличение числа приборов вряд ли оправдано, так как погрешность
∑
∆ не
может стать меньше погрешности образцовых средств измерений,
используемых для их поверки.
Другой путь решения задачи таков. Выберем максимальное и
минимальное из показаний приборов: х
тах
и х
т1п
. Удостоверимся в том, что
(
)
∆≤− 2
minmax
xx
(8-11)
Если неравенство (8-11) не выполняется,
это говорит о том, что в измерении участвует
прибор с недопустимо большой
погрешностью или что какие-то из влияющих
величин изменяются слишком значительно.
Следует выявить и устранить причину этого
явления, т. е. добиться выполнения
неравенства (8-11).
На рис. 8-1 условно изображены
показания
max
x и
min
x и около них отложены интервалы, соответствующие
пределам допускаемых погрешностей
∆
±
.
Истинное значение измеряемой величины должно лежать на том
участке поля допуска, который одновременно принадлежит и прибору с
показанием
max
x , и прибору с показанием
min
x . ЭТОТ участок на рисунке
заштрихован. Его границы определяют уточненное поле допуска.
За оценку измеряемой величины естественно принять середину
интервала
minmax
xx − , которая находится из соотношения
2
~
minmax
xx
A
−
= .
(8-12)
Координата точки
a
, определяющей левую границу погрешности
результата, будет ∆−=
max
xx
a
. Координата точки
b
, которая определяет
правую границу погрешности, равна ∆−=
min
xx
b
. Следовательно, граница
погрешности
1
∆ уточненного результата равна
ab
xAAx −=−=∆
~
~
1
.
Или
22
minmaxminmax
min1
xxxx
x
−
−∆=
−
−∆+=∆ .

Нетрудно заметить, что в пределе, когда ∆=− 2
minmax
xx , погрешность
1
∆
формально получается равной нулю. Однако ясно, что минимальное значение
1
∆ не может быть меньше погрешности тех образцовых средств измерений,
которые использовались для поверки применяемых приборов.
Интересно отметить, что принятая согласно (8-12) оценка измеряемой
величины математически дает наилучшее приближение при равномерном
распределении погрешностей
i
ϑ в пределах
[
]
∆+∆− , [46, стр. 257].
Приведенные соображения позволяют показать справедливость известного положений
метрологии: при параллельном применении средств измерений разной точности точность
результата определяется наиболее точным из них.
Пусть, например, напряжение некоторого источника было одновременно измерено тремя
вольтметрами разной точности, но с одним и тем же верхним пределом диапазона измерений
15 В. Измерения были выполнены в нормальных условиях. В итоге были получены следующие
результаты.
1. Вольтметр кл. 0,5: 05,10
1
=U В, предел допускаемой основной погрешности
075,0
1
=∆ В.
2. Вольтметр кл. 1,0: 9,9
2
=U В, предел допускаемой основной погрешности
15,0
2
=∆ В.
3. Вольтметр кл. 2,5: 7,9
3
=U В, предел допускаемой основной погрешности
375,0
3
=∆ В.
Поскольку измерения выполнены в нормальных условиях, пределы допускаемых
основных погрешностей приборов будем считать равными границам погрешностей измерений.
Чтобы найти дисперсии погрешностей каждого иа результатов, зная пределы
допускаемых погрешностей приборов, нужно знать функции распределений погрешностей
этих приборов по совокупности приборов каждого типа.
Допустим, что погрешности приборов каждого типа имеют равномерное распределение.
Тогда получим
3
ii
∆=σ .
Найдем веса результатов. Поскольку все приборы имеют один и тот же верхний предел
диапазона измерений, то расчет можно вести по пределам приведенной погрешности
приборов:
,4
25,0
11
2
1
'
1
==
∆
=g ,1
1
2
2
'
2
=
∆
=g .16,0
25,6
11
2
3
'
3
==
∆
=g
Отсюда
03,0
16,5
16,0
,20,0
16,5
20,0
,77,0
16,5
4
3
1
'
'
3
3
3
1
'
'
2
2
3
1
'
'
1
1
======
===
∑∑
∑
==
=
i
i
i
i
i
i
g
g
g
g
g
g
g
g
g
Теперь найдем среднее взвешенное
01,107,903,09,92,005,1077,0
~
3
1
=⋅+⋅+⋅==
∑
=i
ii
UgU В.
Границу погрешности среднего взвешенного можно найти по формуле (6-9) для
погрешности результата косвенных измерений:
( ) ( )
( )
.066,0103,1933
375,003,010152,0105,777,0
~
4
22
2
22
2
22
3
1
22
kk
k
gkU
i
ii
=⋅++=
=⋅+⋅+⋅=
=∆=∆
−
−−
=
∑
Принимая, как обычно, 95,0
=
α
, берем 1,1
=
k и находим 07,0
~
=∆U В.
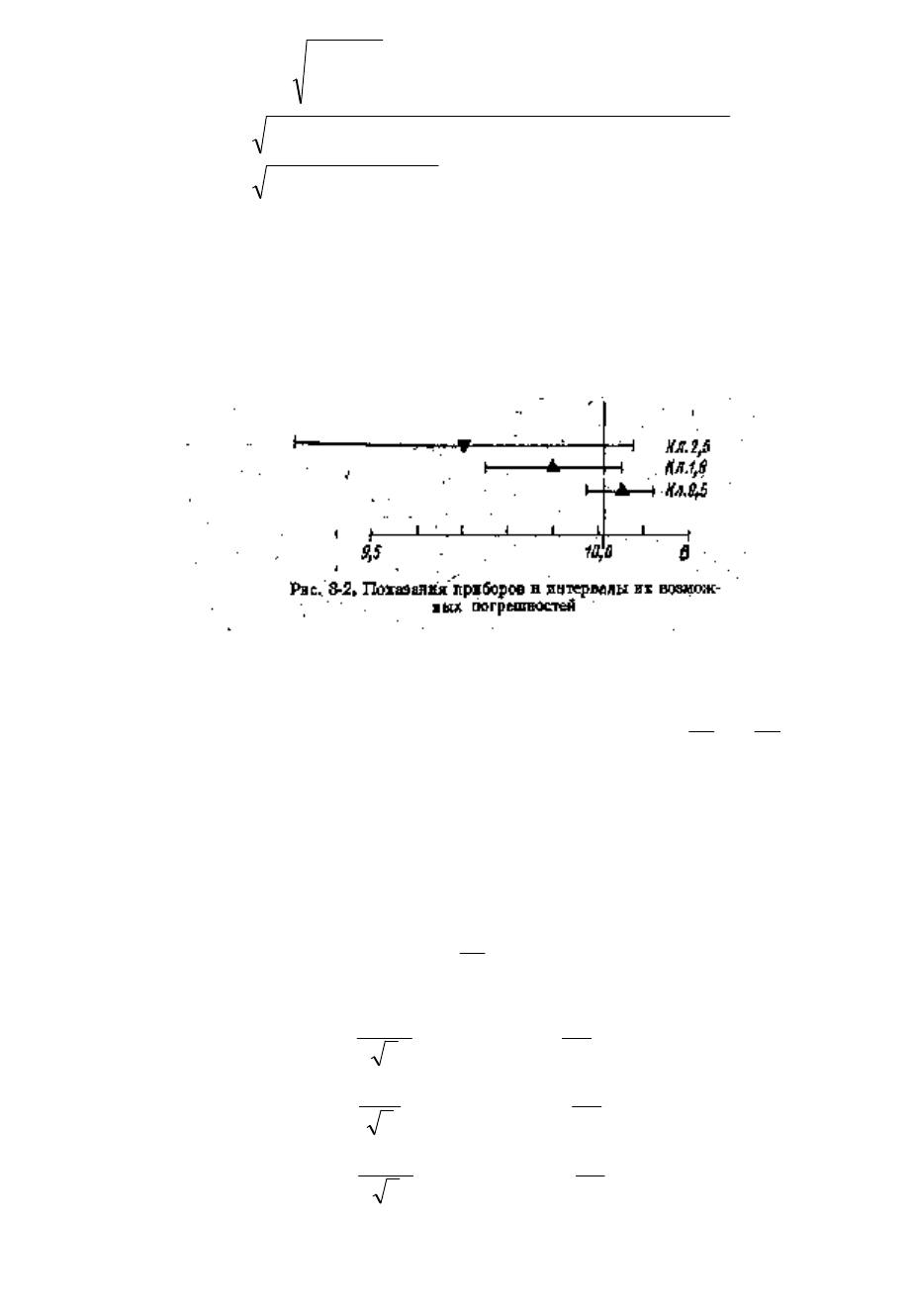
На рис. 8-2 нанесены показания всех трех приборов и отмечены пределы допускаемых
погрешностей приборов. Там же отмечено полученное среднее взвешенное. Это значение
осталось в поле допуска наиболее точного результата, но несколько сместилось в сторону
показаний менее точных приборов, что естественно. Границы погрешности результата
уменьшились незначительно по сравнению с погрешностью наиболее точного из слагаемых.
Если бы мы приняли все распределения за нормальные, усеченные на одном и том же
уровне путем отбраковки приборов с погрешностью, превышающей
=
++
constzz
2
1
2
1 αα
σ
, то
веса бы не изменились и среднее взвешенное осталось бы тем же, что мы нашли выше.
Изменилась бы лишь оценка границ погрешности, так как ее теперь следует вычислять по
формуле (6-11).
Получим
(
)
066,0
~
'
=∆U В. Однако различие между
U
~
∆
и
(
)
'
~
U∆ несущественно.
Посмотрим, что было бы при разных видах распределений у разных приборов. Пусть,
например, совокупности приборов кл. 0,5 и 1,0 имеют равномерное, а приборы кл. 2,5 —
усеченное нормальное распределение, причем 6,2
2
1
=
+α
z .
Тогда
.42
1
,144,0
3
375,0
,78
1
,087,0
3
15,0
,306
1
,043,0
3
075,0
2
3
'
33
2
2
'
22
2
1
'
11
====
====
====
σ
σ
σ
σ
σ
σ
g
g
g

Следовательно,
.10,0
426
42
,18,0
426
78
,72,0
426
306
3
1
'
'
3
3
3
1
'
'
2
2
3
1
'
'
1
1
===
===
===
∑
∑
∑
=
=
=
i
i
i
i
i
i
g
g
g
g
g
g
g
g
g
Отсюда
99,97,91,09,918,005,1072,0
~
1
=⋅+⋅+⋅=U В.
Полученные значения
U
~
и
1
~
U весьма близки. Это свидетельствует о том, что
существенное изменение вида функций распределений не оказывает заметного влияния на
результат.
Рассмотренный выше пример можно было бы решать и графоаналитическим
методом подобно тому, как решалась задача объединения показаний
равноточных приборов. Однако теперь соотношение, определяющее
A
~
, должно
содержать веса слагаемых. В соответствии с изложенными выше
соображениями эти веса можно принять обратно пропорциональными
квадратами пределов допускаемых погрешностей приборов.
ГЛАВА ДЕВЯТАЯ
РАСЧЕТ ПОГРЕШНОСТЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
9-1. Задачи расчета погрешностей средств измерений
Средства измерений чрезвычайно разнообразны, но в связи с их общим
назначением имеют общую теорию погрешностей. Центральной задачей этой
теории является расчет результирующей погрешности средств измерений по
погрешностям их блоков. При этом в первую очередь имеется в виду расчет
основной погрешности средств измерений, как их важнейшей метрологической
характеристики. Расчет дополнительных погрешностей, вызываемых
регламентированными изменениями влияющих величин, или коэффициентов и
функций влияния влияющих величин зависит
