Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment
Подождите немного. Документ загружается.


I;~E,
6.4.1.
Survey
of cascades, investigated. a) Active cascade
(a);
passive cascade
(p);
thcir distance
b
thcir pitches
I,, I,.
b)
Cascade arrangements invcstigated; case
(a),
active cascade upstream,
ase
(b),
active cascade downstream.
3.
Infinitely long vortex sheets, swimming in the x,-direction from the trailins edse
-
1)
of all thc passive profiles with the undisturbed throughflow \,elocity
M,
parallel
("P
-
I,,
the line, charged with bound vortices. The variation with time of the vortex distribu-
tion of these vortex sheets obeys the theorem of Thomson with respect to
the circulation
around each bladc of the passive cascade.
4.
Plane potential flow of an incompressible nonviscous fluid, in which the sheers.
from the trailing edge of the passive cascade, are located don9 a stre,ln~linc.
5.
The temporal arbitrary form of the flow is assumed as deconlposable in its 11:trmonic
portions. One of these is considered here. This one has
a
basic frequency giben by the
geometry of the active cascade.
6.
The cascades have blades of one and the same length
L,
=
L,
(index
'a'
mean5 active,
~ndex
'p'
means passive). Thickness of the profile, its camber and angle of attack are
~nfinitesimnlly small.
p--pp--------
6.4.3.
Basic
idea
of
the
procedure
-
The vortex distribution of the passive cascade
y,
is assumed as
a
temporal harmonic
function with unknown amplitude, which varies with the coordinate of the locus
of
the
considered station of the passive "zero" profile. This is the profile, which carries in
its
mid
chord the origin of the passive
Cartesian
coordinate system. The spatial vortt-x
distribution along the chord of the passive zero profile results from the fact. that at any
\tiition of the passive profile the sum of all induced downwash velocities at an!. instant
inus! be zero. This sum is composed of the followi~g components:
A)
Downwash velocity from the instantaneous vortex distribution of the passive profile
considered.
b)
Downwash velocity from all the neigl~bouring passive profiles, the vortex distribution
of
which oscillates between homologously located points of adjacent profiles with a
.jcfinite phase shift.
-')
Downwash velocity from all the free vortices of the vortex sheets, running from the
'railing edge of the blades of the passive cascade, which also oscillates in homologously
-led points against the adjacent sheet with a definite phase shift, and the amplitudes
'f
which vary due to Tbomson's theorem with respect to the blade circulatio~i
of
the
'assive blade, from which they start.
I)
The downwash velocity of thc active cascade. This moves against the passive cascade
'ith
a
constant velocity
U
in the peripheral direction. Therefore also
U
must
be
added
O
this downwash velocity.

6.4.4.
Rcalizr~tion
of
the
procedure
The
vortex distribution of the steadily operating active cascade is assumed to
be
coniposcd by the first two terms of a Glntrert series
y,
=
A,
(1
+
cos @/sin
9
-
2
A,
sin
2
8.
(6.4
-
1)
Herein
9
dcperlds
on
the coordinate
<,,
which is numbered from the mid-chord of
the
active cascades' zero profile as follows
(,=-coss, 0595~. (6-4
-
2)
That means
t,,
=
I
coincides with the trailing edge of the bladc. With the circulation
I
around the
active
blade
,
+
1
J
~a
(<a)d<a
-
1
follows the instantaneous downwash uelmitgoftheactiv cxcdea
t
thd~ctls
~f*
zero blade
of
the passive cascade as
G,
exp
(A
x,)
exp
(j
h
v
h=
1
ihv,
t
ui
(x,
,
t)a
=
Ui
(x,)~ e
.
The values herein have the foilowing meaning
V,
=
2
n
U/ta,
Lp
'P
*iap
A=Thn---e
,
tp
ta
M,
=
xHh(x
=
1)
+
(x
-
1)
H,(x
=
O),
x
=
A,/(&
-
A,),
Hh=)=Jo[ihn()aeiaa]+Jl[ih()aeiaa],
(6.4-1
H,(x=O)=T--
-
eriaa~, +ihn
-
a
[
hn
L
with
J,
and
J,
as Bessel functions of order zero and one. Generally the Bessel funct
of order
p
is defined
by
U)
(-
1'
(y"'2k
=
C
9
Jp
1=0n(k)Z7(p+k)
2
with
n(k)
=
kn(k
-
1).
228

In
lhc relntiol~s :rbove, the upper sign is valid
if
the active cascade
lies
upstrean1 from the
Pi
,,,;,1e cascade.
6.4.5
List
of
used
symbols
U:
velocity of the active cascade in the peripheral direction against
the
pr~ssive cascade.
~c:
real part
:
pitch
:
stagger angle
L:
length of profile chord
h:
order of the harmonic
:
distance of the two cascades, normal to its axis
,,,:
imaginary units
jndcx
a:
active cascade
index
p:
passive cascade
index
i:
value, which depcnds only on the instantaneous motion, in contrary to the
transient value, depending also on its history.
6.4.6.
Derivation of governing linear integral equation
Thc velocity field of a row of homologously located passive vortex elements is defined
by
[he fact, that two neighbouring vortices are oscillating with a phase shik of
The induced
do\vnwash velocity of all the blades of the passive cascade and its vortex
sheets is compensated by
thc dournwash velocity
ui(xp).
eihV''
of the active cascrtde.
This passive downwash velocity of the whole passive cascade; with its blades of length
L,
=
2
together with the infinitcly loilg vortex sheets swimming from the trailin3 edge of
each blade at its rear end becomes
03
fii
(x,
t),
=
5
7i
(5)
&vt
K
(x,
4)
d4
<=-I
with
integer number belonging to the individual passive blade, and

The
equ;ilization
of
u,(.\-~),,
and
LI~(-K
)
Icilds
to
lhc
fi~iIo\\.iil~
;nlc$r;~l cclrl;~tion Tor
th
P
P
vl>rtcx dist ribt~tii)~l
?,,(<)
Herein
t~~(.u,),
is defined by equation
(,6.4
-5).
Furtheron
we
Itave
k
=
v,
Lpl(2
w,)
as redaced frequency.
6.4.7.
Solution of
integral equation
by
polynomials
following
Lotz
3
:
$
Lot;
has solved the basic linear integral equation
--)
by iotroduction
of
11
58
trigonometric
auxiliary variable and
a
substitution
proposed
by
Scllrtieidler.
ThiiQ
reduces the integral equation of our
.
.
problem into
a
l:rellholrt!
integral
of the first order. For a numerical
comput;ltion
the
Kerncl
K,Ix
-
c)
ior
ti,,
neigi~bouri~lg blades of the passive cascade
is
approxi~ni~tcd
by
a
polynominl
9
3
K,(x
-
()
=
jco
+
c,r
+
jc2r2
+
cjr
+
jc4rJ,
with
r=x-(.
c,
is chosen so, that
I<,(r)
has its exact value in the collsidered point.
The
other constan1
will
be
conlputed
so,
that the integral of its scluarcd error witlli11
-
2
<
r-
5
+
2
becorn,
a minitnuri~. Thus
it
results
with
L
T2
=
1111
(KR)
r2 dr,
0
2
T,
=
1
Re
(S,)
r3dr,
n

6.4.8.
Lift
and moment on
the
passive cascade
\Vith
~~(5,
I)
=
;l(t,
t)
and the circulation around
the
passive blade
+
1
r,
=
r=
5
y(tt
t)d<,
(6.4-
34)
-
1
we
get lift and moment related
to
the mid-chord
of
the considered profile
as
E;
and
MA
are relatcd to a blade
of
width
"one".
Obviously the lift
as
given by
Ktrtrn
and
~orrkovsky holds o11ly for steady flow.
6.4.9.
Discussions of evaluated results
The aforenientioncd theory has been ev;iluated for the case
b
=
0,l
L,,
a relation, which rnay be
realized
at the outcr parts of a tubillar turbine with a fully opened runner. Furthermore it has bccn
assurned that
t,
=
t,,
a,
=
45",
(tiL),
=
1.
Computation has been carried
01.11
for case a) with the
activc cascade upbtrcam of the passive one and case b) with the active cascade downstream of the
p;issive one.
Furthermore
the computation has been made for the case
x
=
1
ant1
z
=
0.
For
./:
=
0
111c angle of attack of the active cascadc bccomes zero. In this case thc profile consists of
a
circular
arc
wlth the flow along its chord, duc to
A,
=
0.
For
x
=
1
the active cascade consists of plane plates
with a
finite ar~glc of attack duc to
A,
=
0.
A
first computation shows that only the first harmonic need be considered. In Fig.
6.4.2
wc
see t;:e
rcl;itivc lift
amplitude
of the first harmonic for the case a) and b) and
i:
=
1,
z
=
0.
The result shows relative
lift
amplitudes up to
20%
for stagger angles between
0"
and
40"
of the
passive cascade,
if
the active cascade is arranged downstrcam and operates nith an angle of attack
against a plate as profile
(x
=
1).
This case may be realized under fully opened runner blades in the
cylilldrical section of a tubular turbine near !he throat ring. Even if the actual problem is not exactly
a
phne one, one can reduce it approximately by conformal mapping of the outer strcamsurface into
a
plane.
The same can be done with a Kaplan turbine of cylindrical wickct gates. Here the distance is usually
@cater between wickct gates and runner blades.
6.4.3
demonstrates for the case
a,
=
a.
=
4S0,
that the relatire lift amplitude of the first
hamlonic increases with
decreasing
ratio
t,,/t,.
That means: The higher the blade number of the
"imulating active cascade the higher the 11ft amplitude. Similar results are obtained for the
'mplitudes of the moments about the mid-chord of tee blade.
nis holds Inore for
an
active cascadc upstream.
In
the actual case of the downstream runner as the
wive cascade
we
have usually very low values of
I
Jt.
as the runner has
z
=
4
to
5
blades and the
distributor has 12 to 24 wickct gates. Therefore in this case the wicket gates are not seriously
uimulated by vibrations.

I
so-
f5,
P/
msr
a
casr
b
Kemps
and
Sears
Fig.
6.4.2.
Cornplcx amplitudes of the unsteady lift as a h~nction of the stagger angle
a,
on the
passive cascade, for the case
a,
=
45", t,/t,
;.
1,
and
Lp/tp
=
1;
ordcr
of
harmonics
h
=
1.
4
Fig.
6.43.
Complex ampli-
.i
tudes of the unsteady lift
$
moment as
a
function of the
pitch/chord ratio
t,lLP
on
the passive cascade, for the
4
casr
a,
=
a,
=
45", tdt,
=
1,
a
Ir
=
1.
i
~
When the machine operates with a reversed flow as
a
pump or
a
tidal turbine, then the :tction of
th
fluc:r(~tions of downsiream located wicket gates, now acting as diffusers, on the impeller or runne
blades may be dangerous. This danger is enlarged by wakes.
-
6.4.10.
Conclusion
of
practical
results,
effect
of
wakes
As measurements, carried out
by
Castorph
[6.29],
at Tecllnical University, Munich. have shown,
wakes are relevant also in the
c:se of a vertical Kaplan turbine, when they act from the upstr
232
loc;,t~d
wicket gatcs on 111e
outer
section
of
the runner bladc.
llerc
indecd thc slrciln~uisc dist;~~~.~
belw~,c~i the cxit of
a
cyli~idrical gate and thc runner vane nlay be rather short.
TI,^
mcastlrcnlcnts Ii;~\.c bccn carried out with
n
spccial six port micrc;simiconductor ~ectoriul
probe
of quick rcsponsc which enables vibrations up to
5000
cyclcs to be 111dic;lted. Such
;I
prob;.
(Cap.
9.5)
indiclltcs
bchind
the runner likewise the w;~kes produccd
by
the runner blndcs, :itso. thc
~roduced
by
tllc picket gatcs, which have been cut into pieces
by
the runner blades. Thc
of the measu~cd
unsteadiness
causcd
by
a
wake can
bc
predicted duc to the nleasurelnenrs
by
the
foliowing method.
~~~ordillg
to
I(et??p
and
Sears
16.301,
the
dowriwash velocity
of
an
active
cascade on
n
psive cascade downstream can
be
described
by
IIerc
u,
is
the
deviation of the velocity from the average of the adjacent \/elocities
within
the middle
of
the
wake.
G
is
given
by
G
=
L,
Y
sin
(2,
+
ct.1
cxp
{-
(---)
JI;~
L,
It\'
t,
cos
a,
2
cos
2,
I,
(6.4
-
38)
(sin
ct,
+
cos
r,
tail
r,)
.
cos
2"
I
2
]'is
the
measured breadth
of
thc
wakc.
For
centrifugal impeller-s
h:L,
can
be
1.er-y
srnall.
Therefore the action of the relatively large impeller wakes
on
a
bladcd
difTuser
must
be
raken
into accocnt. The
aforementioned
results stro!lgly
decrease
wirhthx
distance
b
cf
the
two
cascades. 'rliis influences strongly
~hc
do~rnwa>h velocity.
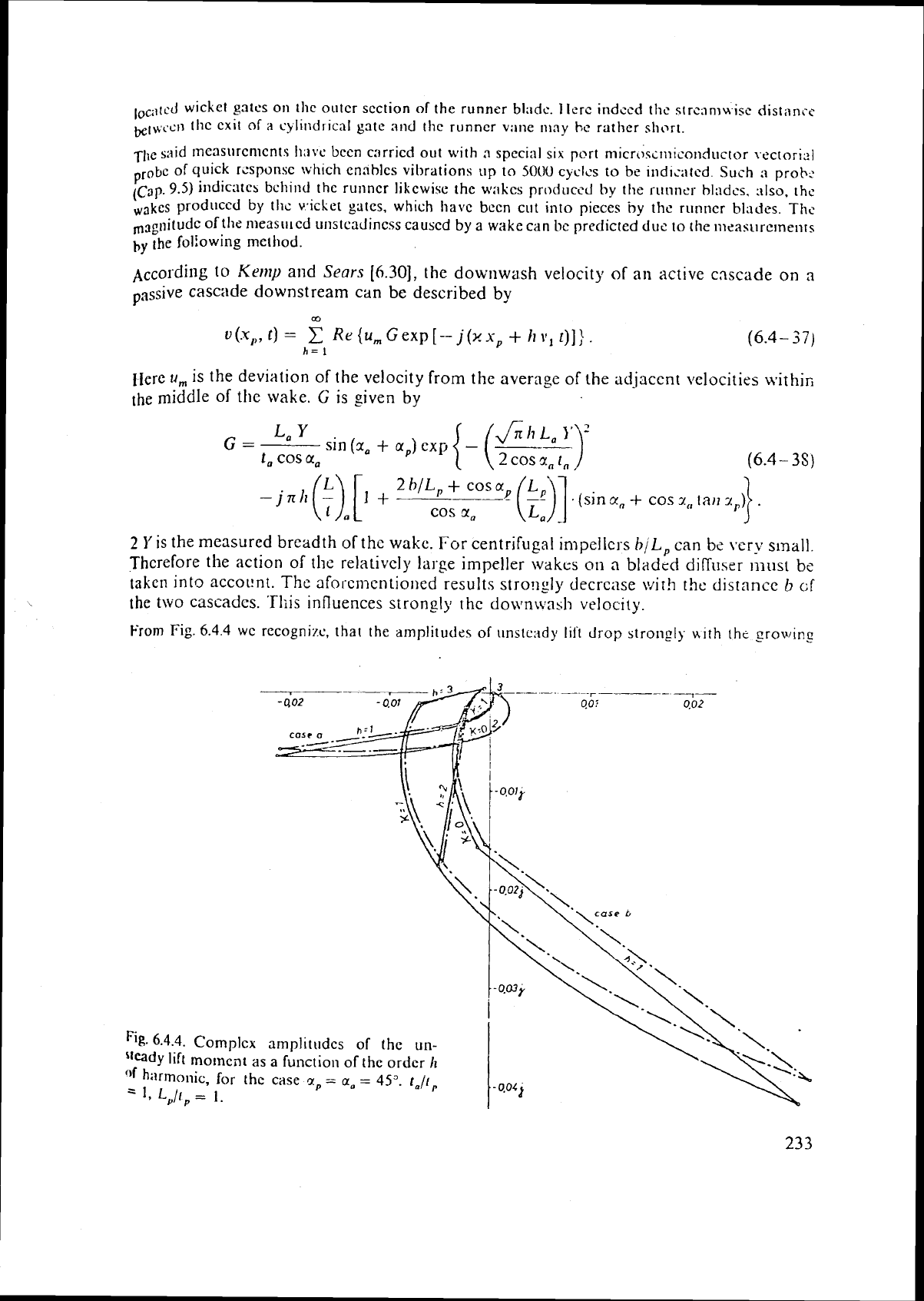
From
Fig.
6.4.4
we
recognize,
that
the
amplitudes of unhtcady
I~ft
drop ~trollgl~ ~ith thc growir??
Fig.
6.4.4.
Complcr
amplitudes
of the un-
steady
lift
moment as
a
function of the order
Ii
~f
h;lrmonic, for ihe case
I.,
=
on
=
45'.
fa//,
-
.-~041
-
1,
L,/l,
=
1.

orclcr
tltc Ii;~r~iio~~~c
'I!'.
I
111.1-cI;)rc tllc first I~;~rliionic nl':ll~y
IIIISIC;I~~~I~~SS
is us11:1IIy s~lllicicnt witl,
rc\pccl to
I
l;c
cfft'ct
of
I~II\IC;I(~II~C\S.
An u~lstca~lilics.;
of
rhc rcl;~tivc 1101v in tllc rurlllcr or impcllcr rcsi~lts also froni
no11
uxisymrnetry
of
rhc
no\v
in
tllc spirill c;tsit~:. i:spcci;~lIy 11ic rcgion nc;lr the tongue of
tile
spiral casing
may
show
10
to 15'% dcv~;~rinn Troni ;tvcr;igc ilow
long
the pcriphcry. Sucli
a
deviation may
disappear
;tt some
working points.
Unfortt~nat~ly
it
c;1111101 disappe;lr within thc wlioli opcr;~tion:il
range
of
a
ti~rbinc. This
unsteadiness
acts
011
the runner bl;tclc as
a
very big wukc.
It
attacks one runncr blade
;IS
a
wholc. Such
n
fluctuating
force may
C;~LI?;C
strorig ovcrstrcss
in
~IIC
bl;idc root scction of
iI
K:lplnn runner ncar the hub
cspecii~lly in
connection
with fiitig~le ~ii~cts uf C'llromium steel blatles. Accortling to thc geometry
of
the bl;lc!t.lcss spi~cc bctv:ccn the wicker ptcs ;lnd thc runncr and due to the
IISLI;II
distribution
the Inorncnt
of
monicntum before thc I-unncr.
any
perturbation
I'rorn thc distributor in
a
Kaplan
turbine acts much stroi~gc~.
ilt
tile o~ltcr p;~rts of
a
blndc.
fIcrc thcse hydrodynamic forccs have
a
largc monicnt arm :\gainst the root section of the blade near
the hub.
A
similar strong vibrating force acting on
a
long lnorncnt am1 exists also in a Francis turbine
~hcn the shroud is oniittccl. Hcrc the runncr hladcs clnmpcd cn thc one sick may be badly
o\.erstrcsscd at thc inner hlade cross scction. Thc eifcc! in a Kaplan turbine is more serious
as
it
opcrntes ubuully
ti
ith
a
semi-spira! casing a5 distributor. This element produces more
deviation
from
the axial syrnrnctrq of the inflow of the runner thxn the usual hpiral casing would do.
Thc
aboi e
procedure
from
hl.
Lotz
is based on cascades of skclztons and
the
assumption of a steady
flow
through thc activc cnscadc. LI~RIIIILITI
[6.31;
6.321
has dcvclopcd
a
rigorous nicthorl by a time step
proccdarc.
th;tt
sciount.; for arbitrarily s!iapcd profiles with unstcacly flow in both the cascades.
This method
h:ts
bccn partly expcrimcntnlly reconfirrncd
by
tcsts of Lahrn and
Ccrstorpli
[6.33;
6.341
bith the aid of quickly responding semi-conductor probes. Tcsts of
Casrorpl~
[6.35]
reveal also the
influence of shock waves on the unsteii.dy bchaviour.
Th;
influencc
of
wakes has bccn recently invcsti_gatctl by L~rhrn
[6.33].
The effects
resulting
from
cascactes upstream and do\vnstream
of
n
considered cascade have been recently trsated
and
t:ieasured
by
D.
Cusrorplt :1nd H~lb~~~~stcirrcr
[(i.36].
The influencc of wakes on an unsteady flow
tllrough casc;ldss in t,indcm arrangement moving rclative
tc
each other has bcen investigated by
Kr!lntnrer
[6.37]
on
the
base
of I-iettl~trrt'~ rigcrous illc~~y. Fa~tclli and Siccai.Oi
[6.38]
have treated the
rcsponsc
of
turbornachinc~ with cascadcs to the oscillations
in
the penstock.
6.5.
Distribution
of
meridional velocity
normal
to
stream face
6.5.1.
Introduction
In
the foregoing section the
fl~w
within axisymmetric stream fzces or flow laminae
beet? invcstisated under the assumption of
a
given flow-linked meridiona! velocity.
mixed flow rotors with a
larper span
in
the vaned par: the problem arises how
t
meridional component of velocity is distributed over the span
b
between the outer
a
inner
shroud
(hub).
For simplification of the problem a practical approach is made by
assurning
a
uni
distribution of the meridional and whirl component
c,,
and
c,
of the absolute flow i
peripheral direction.
To
obtain the influence of vane geometry, the angle
P
between
relative flow and periphery. is
;ljsumed to bc given. This angle depends according
(6.5-
13)
on the given pattern sections and radial sections of the vane, and the geome
cf
an asisymrnetric streamface, also
determined
by that
of
the inner and outer shro
234
~~suming a flow along the vane, the influence of vane geometry is :~ccourited for \\.ithin
tllc fl-amc of simplc assumptions. The following consider;ltion deals only u.ith velocities
pressure
;is
they really occur within the fluid.
In
an
ideal fluid here assumed, according to
Poscal's
theorem, the pressure at
a
certain
stati~~~ is independe~lt of the orientation of
a
face. The idea sonletinles used oi all
inlaginary force, normal to the vane, but uniformly distributed over the pitch [6.1; 6.391
is left aside.
6.5.2.
Special assumptions
a)
Infinite numbcr of vanes reduced to their skeletons,
b)
steady absolute flow on axisymmetric stream faces,
c)
relative flow along the vane, vane angle
P
given,
d)
gravity
neglected
as not contributing to the velocity distribution,
e)
runner loss linked to individual flow lan~ina, like that of developed flow in a
straight pipe,
f)
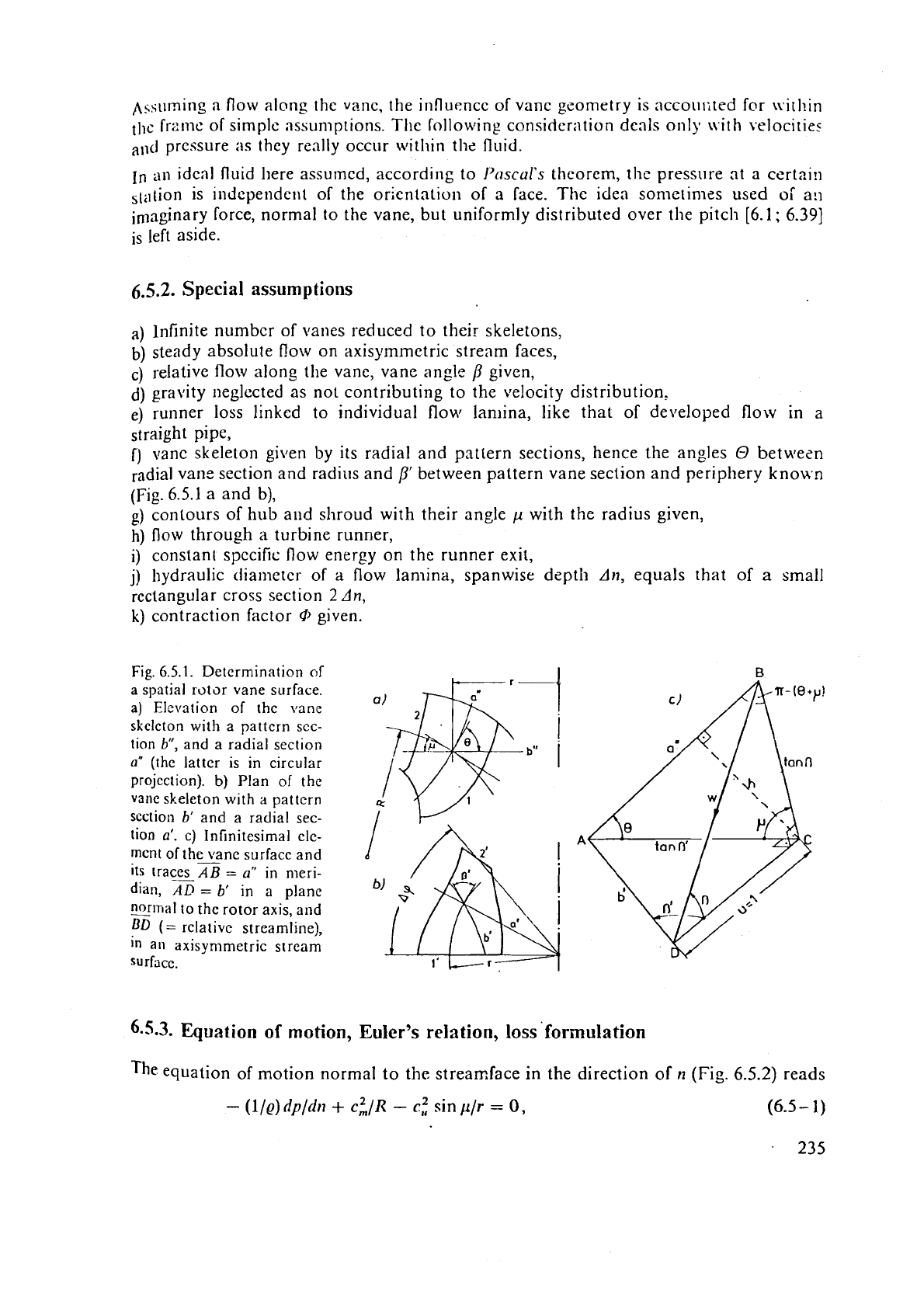
vane skeleton given
by
its radial and pattern sections, hence the angles
O
betwesn
radial vane section and radius and
8'
between pattern vane section and periphery known
(Fig.
6.5.1
a and b),
I)
contours of hub and shroud with their angle
p
with the radius given,
h)
flow
through
a
turbine runner,
i)
constant spccific flow energy on the runner exit,
j)
hydraulic (lia~netcr of
a
flow lamina, spanwise depth
An,
equals that of
a
small
rectangular cross section
2
An,
k)
contraction factor
Q)
given.
Fig.
6.5.1.
Determination
of
a
spatial rotor vane surface.
a)
Elevation of the \lane
skeleton with a pattern scc-
tion
b",
and a radial section
a"
(the latter is
in
circular
projection).
b)
Plan of the
vane skeleton with
a
pattcrn
scction
b'
and a radial sec-
tion
a'.
c) Infinitesimal cle-
mcnt
of
the vane surface and
its
traces
AB
=
a"
in meri-
dian,
A%
=
b'
in
a plane
normal to the rotor axis, and
-
BD
(=
rclativc streamline),
in
an
axisymmetric stream
surface.
6.5.3.
Equation of motion,
Euler's
relation, loss'formulation
The
equation of motion normal to the streamface in the direction of
n
(Fig. 6.5.2) reads
-
(11~)
dpldrt
+
c:,/R
-
ci
sin
p/r
=
0,
(6.5
-
1)

Fig.
6.5.2.
Unit
fluid
mass
between
adjacent
axisymn~ctric stream faces in a meridian.
a)
ring
vortex. possiblc
at
part
load.
b)
relation between
dl[,
i?r.
dp.
Thc
location
L1.~:,
of !he outer edge
of
the ring vortex
a)
results from
(6.5-10)
with
Ay=-y(~=0)=-1:A~,=
1/C/,M-f2A,),
where
f,,,
f,,,
are
mean
values of
f,,f,
within
Ax,.
where c, is the meridional velocity, c, the absolute whirl velocity, R the radius
of
streamline curvature in the meridian, p the angle between the streamline and radius in
the meridian, r the distance from the rotor axis.
The application of
Euler's
equation bctween the station under consideration and station
1
at rlinrler outlet, with respect to a draft tube loss, expresscd by C,c:,/2 and a streamline-
bound runner loss, between the
poinr considered and the runner exit dpi/e, gives
where
p,
is the pressure on the tailwater level.
According to assumptions
e)
and
j)
and with respect to the relations from the velocity
:riang!e
\v
=
c,/sin
p
and the relative streamline element
(is,
0s
=
dr/(cos
,u
sin
/3),
with
a
constant loss coefficient
I,
the ruriner loss is formulated by means of
r
I
[C
ci/(~n sin3
B
cos p)] (lr
-
1
[I
ci,/(~n sin'
/3
cus a)] dr
.J
const cons1
I
6.5.4.
ci
as
a
function
of
monient
of
momentum
c,
r
The pressure term
-
(11~) dp/dn in (6.5-
1)
is eliminated by inserting
it
from the relatio
(6.5-2),
differentiated with respect to
n
accounting for assumption
i),
and f~r (6.5-3).
0
this occasion,
dyi/e
has to be differentiated with respect to the upper boundary of th
respective,
definite integrals in (6.5-3).
For this renscn also the obvious relations drlcln
=
-
sin
p,
and continuity c,rA
=
c,,
r,
All,
have to be taken into account. With the last but one relation the expressio
d(ct/2)idn
-
c,Z sin plr, can be reduced finally to (c,/r) d(c,r)/dn. Hence
dcrldn
+
(2/R
+
[C/(2 An)] {tan p/sin3
P
-
[r
Ani(r, An
,)]
tan
/sin3
PI})
C
=
2
[(o
r
-
c,)/r] d (c, r)/dn
.
-
This linear differential equation for
c:
is also valid for vanishing
c,
=
0
(stalled regio
as shown in Fig. 6.5.2).
It
offers the opportunity to design
a
runner as a function of
an
desired distribution of the moment
of
momentum
c,
r by means of
a
step by step pro
dure. For the start
C
might be put to zero.
236
