Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment
Подождите немного. Документ загружается.


,,~llcre
C,
through
C4
are functions of the
parameters
of
the cascade, nan~ely
111,:
pitch to
chord ratio
t/L
and thc
angle
13,
the
straight carrier of bound vortices 111;lkes
uritll
tl~e
p,
stands for the untlisturbed flow direction, the ircro
lift
direction.
Uncisr
the
assunlption of
3
small angle of attack
do,
the angle
13,
the zero
lift
direction nlakcs
the circumference can be substituted for
Pa,.
Table 6.2.1 cont'lins the vi\lucs
C,
C4 as functions of the so-called cascade paranleters
r/L
and
13,.
Table 6.2.1. The cascade parameters C,, C,, C,, C, as a function of
/3,
and
r/L.
Analogous to (6.2-42) from
(,,
the zero angle of attack is obtained for
a
certain skeleton
having the parzmeters
Si
and hence
K,
according
to
(6.2
-
37)
and being within a cascade,
having the parameters
t/L
and
/3,
and consequently the coeficients C,, C,,
C,
Similar to (6.2-43) the physical angle of attack
6,
is introduced. This yields the lift
cocficient of the profile in the cascade with the features C,, C4 as
a
function of the
~hysical angle of attack as
A
retrospective view of the achievements with respect to the probleins of cascades (b)
shows that problcms
1)
and
3)
arc solved by (6.2-48) and (6.2-47). Problem 2) is solved

by
(lividins
(6.2
-45)
in
{,,
froln (6.2
-
44)
with the assu~nptioti
(j,,
=
O,,,;.
This results
in
the cascade fiictor
x
=
i,,/~,,(J,,
-
So,)
=
(C,lC,)l(2 n)
Hcnce
C,,
=
2nx3,.
It is seen from the
z
(tlL, /?,)-plot
(Fig.
6.2.5), that the cascade factor
x
deviates strongly
from unity in the rangc of pitch chord ratios about
1.
But this corresponds to the
range mostly used in axial machines
(6.81.
The large
x
at the rotor vane tip section
(/I,
here about
1
8")
makes the
lift
coeficient and
with it the susceptibility to cavitation there rather sensitive to smr~ll errors of
vane
position.
Fig.
6.2.5.
Graph of thc cascade factor
x
of a straight
cascade as a function of its pitch to chord ratio
t/L
and
the angle
Do
of its zcro lift direction.
.
The
Kutta
condition (6.2-23) at the rearward edge of
a
rotor vane requires
a
compensa-
tion
c.f
any flow induced by the residual cascade and tending
to
circulate about this edge
by means of
a
change in circulation
of
the blade considered. This effect mainly dictates
the lift coefficient and herewith
x.
3,
4
An approaching singularity method, similar to that of
Birnbnunt,
but also valid for profiles
o(
relatively small thickness, has been given by
Schlickting
[6.10].
Rnobe
[6.11]
shows that the finite
thickness of a profile mainly changes the zero lift direction of the cascade.
I
I
X
rigorous method for an ideal flow through a cascade has been developed by
F.
Weinig
[6.9].
hi?;
method uses conformal mapping to transform the contours of a straight cascade of straight skeletom
into a circular contour.
By
means of conforlnal
napp ping,
the domain, which corresporids to the
florv"
about one skeleton, is expanded into a plane.
Simultaneously
the internal domain between the twq
stasnation points on the skeleton is tralisforn~ed .into
a
circular contour. Thus
a
treatment of the,
plane potential flow through the cascade is reduced to that around a circular
cylinder.
This
is
done<
by making the imaginary pzrt of a regular function of a complex variable
z
a streamline and the
rd3
part of this func:ion an eqi~ipotential line. h'ence any conformal mapping must result in the same
solution as the plane singulality nicthod, since both methods assume
a
plane potential flow.
d
f

6.3.
Some
prohlcms
of
steady
flow through
cascades
6.3.1.
The
circular cascade
with
axisymmetric stream surfaces
jmagine
a
stationary cascade (e.g., wicket gates) passed by
3
potential
flow
on
axisymnletri~ and equidistant stream faces
(Fig.
6.3.1 a). The. solution of the illdirect
(Cap.
6.2)
can be reduced to the above treated flow through
a
straight cascade
by conformal transformation of the axisymmetric stream face onto a plane.
First the real stream face is conformally mapped on a coaxial circular cylinder
(Fig. 6.3.1 b). The unrolling of the cylinder into a plane converts the circular cascade inlo
a straight cascade.
Fig.
6.3.1.
Reduction of an axisyn~metric cascade flow in
a
X,
Y-surface to the flow around
a
straight cascade in the
x-,
y-plane. a) Axisymnietric flow
in
a layer of constant depth
h
through
a
circular cascade in the
X,
Y-surface.
b)
Con-
formal mapping of
an
elementary
trianglc in thc
X,
Y-surface
to one
in
the cyliridrical
x,
y-surface, developable onto a
x,
y-plane.
The conlormal mapping is carried out such that the corresponding peripheral
components of an elementary extension on
the real face, having a variable radius
I.,
and
on the
cylirldrical image face, having
a
constant radius r,, are enclosed between adjacent
meridians, making an azimuth
dcp to each other. Hence the real peripheral component
rdcp
is
represented
by
an image r,
dq
and the azimuth of a real point equals that of its
image.
Denoting the corresponding meridional components
of
this length by
ds
and
dX
on the
image face and the real face, the similarity of elementary triangles on both the faces
requires
dx/(r, dq)
=
dX/(r
dq).
Thus the meridional arc
X
of
a point in the real fzce is
X
represented by
a
length of
x
=
r,
I
dX/r. The above yields the local length scale of the
mapping
o
Assume both the hces to be covered with a layer of the
same
depth passed by the same
flow. Hence the local velocity scale
219

w:l~crc
c
and
C
;Ire thc
velocities
duc to ~hc image ant1 real face. Obviciusly the scale
of
circlllation being
hf,
1W,
is
constant. See also [6.12; 6.131, [5.2].
6.3.2.
The
direct problem of a cascade
in
potential
flow
This problem concerns the layout of
a
cascade including its profiles for given velocity
triang!cs at its inlet and outlet. With respect to
lift
coefficient and cavitation sensitivity,
the contour velocity of this cascade is usually somewhat restricted. The problem is
considered in the simpler and better known case of a plane steady potential flow through
a straight cascade.
Thereby full use call be made of tile findings of Cap. 6.2 concerning the indirect problem
duc to the straight cascade. The governing integral equation (6.2-
19),
in its summed
version (6.2-20) is the starting point, to solve the direct problenl, which strictly speaking
can be rnzde only
by
means of relaxation methods and some additional conditions.
In
the case of the direct problem the so-called deflection trainglc is given
(Fig.
6.2.1 a). It
consists of the velocities
c,
and
c,
upstream and downstream of the cascade and hence
the so called defleclion dc,
=
cY2
-
c,, (in the case of a pump). Note that
c
in these
considerations is always the velocity relative to the cascade.
For the design of an axial runner,
gH,
Q,
and hence also the type number
11,
=
(11
Q1j2,/(C!
H)~~~
are known. This gives the angular velocity
a.
The vane number
z
follows from the head
fj.
Expressing
Euler's
equation (see Cap. 5.3) for axial turbines in
terias
of runiler vane circulation gives
r
=
2
n
y
H
q,/(z
el).
With dc,,
r
(6.2-
15),
also the
pitch
r
is known and then by
n
r
=
AC,~
=
$c(s)~s
=
c(sV)h (6.3-3)
v=
1
---
n
also
C
c(sv)h is given. Here the symbois are used in context with (6.2-20). There with
...
=
1
c,
=
constant, the above sum appears in connection with the last term
on
the right hand
side.
It appears that in an axial rotor of a hydro turbo machine
the lift coeflicient
CA,
is
prescribed. On its
innermost cylindrical section close to the hub
(,,
becomes highest.
This is
n
consequence of the so-called "cascade dimensioning relation" of Bnlrursfeld
[6.14]
following from (6.3-3) in (6.2-35) as
CAG
=
(2
t/L)
AC,/W,
-
(6.3-4)
Hence in the innermost cylindrical section of a rotor vane, an upper lirnit of
LA,,
has to
be set,
to
prevent stall. The outermost cylindrical section is most likely to cavitatc;
Because of a rise of the cavitation-linked factor
1,
(Cap.
8.2)
with CA,, formulated by
Raabe
[:.I
I]
also a limit of
CA,
must be fixed in this vane section.
.4
Hence at dc,,
rvl
known from the deflection triangle (containing also
w,
as the geometric
meal? value of
)v;
and
w,),
at
L,
prescribed, the pitch to chord ratio
tjL
yields
from
(6.3-3). From the velocity triangles also the ang!e
a,
of the influx
is
known.
@
2
Consider now again the governing equation (6.2-20). The direct problern consists in
tb
n
determination of the angle
a(ri)
of the vane contour at given a,,
cm,
r
=
1
c(sJ
h.
wid
b
the contour unknown, also the points
zi
and hence the functions
1,
and xgccording
td

(6.2-
21)
to (6.2- 22) arc not given. Obviously thc problem must be solved by trial and
cssor-
TO
introduce also the known
t/L
in the relation ((2-20), the following ratio
k
is used
k
corresponds to the ratio of contour length
n
h
to twice the chord L. Ob\riously this
depends on the profile thickness and is about
k
=
1,Ol for thin PI-ofilzs at the outermost
cy]ind~-ical vane section and about
k
=
1,l for the thickest innermost cylindrical vane
section (thick for reasons of solidity).
Fro111 this it is realized, that
k
may bc fixed prefiminarily. Introducing now from the last
relation
12
=
2
k
L/n into the basic equation (6.2-20) this then contains the known and
pitch to chord ratio. Reducing this relation to the contour angle and accountin2
for (6.3-
3)
gives
i
cot
a
(zi)
=
dc,/(2
c,,)
+
cot
a,
+
(Llt) (kln)
v=
1
11
(6.3 6)
N
=
1
+
('1')
C
[c
(sv)lcn,l
fx
(~i,
z,).
v=
1
The condition for the closure of the polygon formed by the elements of the contour reads
11
C
It cos a(zi)
=
0
v=
l
To solve the direct problcm,
Inouc
et 31. use cascade data [6.15].
6.3.3.
The
indirect problem of the
flow
through
a
mixed
flow rotor
on
axisy~nrnetric stream
faccs
of
constant depth
Here again the solution may be facilitated by a coi~forrnal mapping of the circular cascade
in
the real axisymnietric flo~v plane into a straight cascade within the image plane.
A
rotor
is considered (Fig.
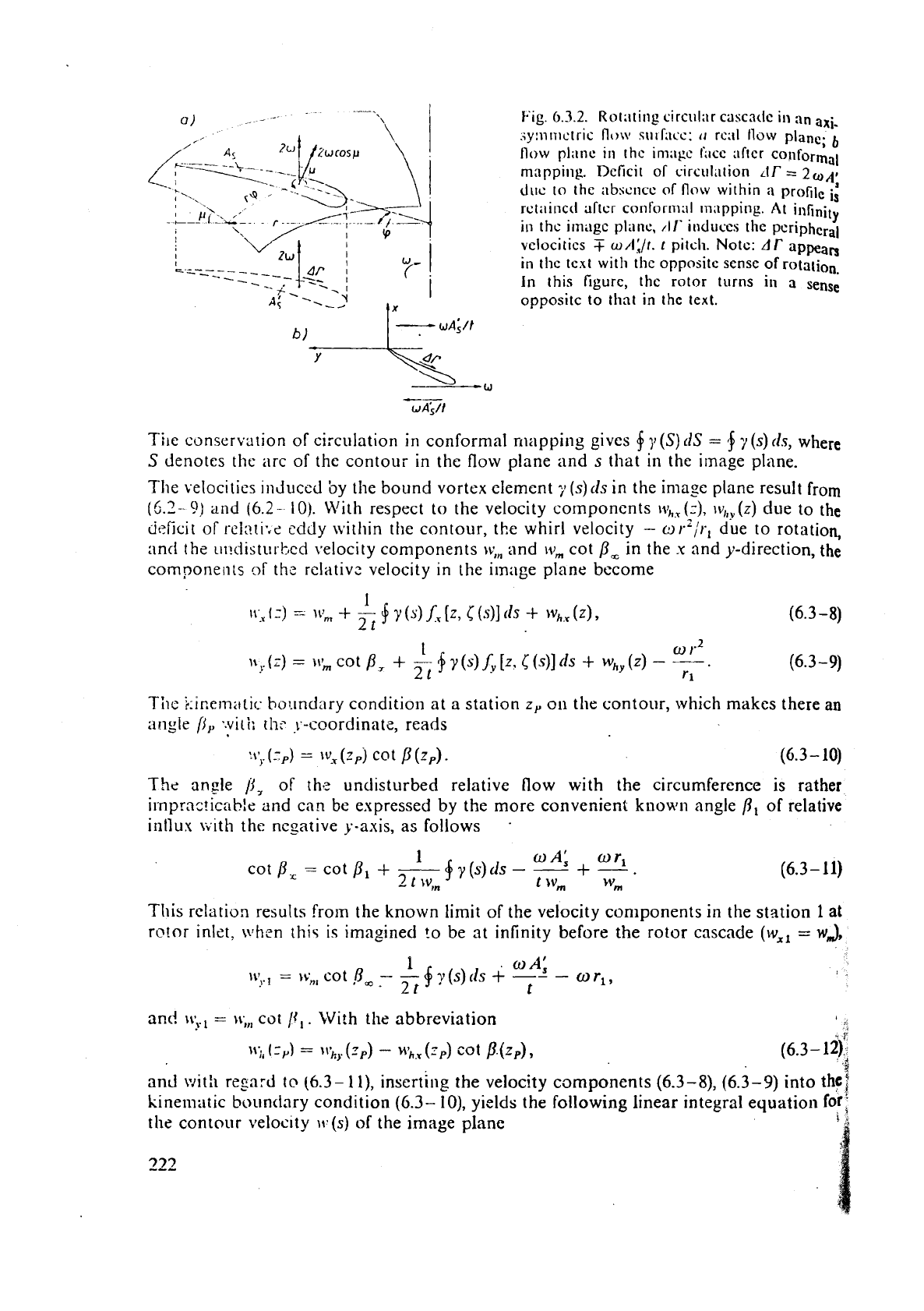
6.3.2), which rotates with the angular velocity
w
in the y-direction. Let
11
be the angle, a normal to the flow plane makes with the rotor axis.
The
absolute flow
shall be irrotational. IIence for an observer on the roating frame of reference, at
a
station
of radius r, the fluid seems to
move in the circumferential direction with a whirl lrelocity
-
r
a.
At a velocity scale from (6.3-2), this corresponds to a peripheral vclocit)r
-
w
r2,'r,
in
the image plane. Note in Fig. 6.3.2
w
is negative.
The
absence of relative eddy
-t
2
o
cos
j!,
within the vane contour of the flow plane and
its image plane, induces the velocities
\u,,(z) and
why
(2)
in
the throughflow and peripheral
direction respectively at a point
z(x,
y)
of the image plane.
They
are function of
2co
cos
[r
and the vane's cross sectional area
A,
in the flow plane
(Fig. 6.3.2). Accounting for this deficit of relative eddy
2
o
cos
p,
which is retained under
conformal mapping, and recalling the circulation around a surface element
dA,
to be
2
o
cos
jr
dA,,
the velocities
w,,,
(z)
and
w,,, (2)
can be approximately calculated
by
relations
similar to (6.2-9), (6.2-
lo),
where
y(s)
and
s
have to be changed a little. 'To this, imagine
dA,
=
h
(is,
where
11
is the local thickness of the profile
in
the flow plane, and ds its length
dong the vane skeleton, with the arc coordinate s.
Now
the line integrals
in
(6.2-9),
(6.2-
10)
are transformed into integrals along the skeleton s, in which cos
p
and
h
are
known functions of
s.
I
--.
0)
P1g.
6.3.2.
Roti~ting circ~~l;~r cascade in an
axi.
.;y:nirictric
flo\\f
su~fii~c:
(I
rc;ll /low
plant-
b
flow
pl;~ne
in
thc im;lpc i;~ce :~ftcr ~~lifo~&~~
mapping. Deficit of c~rcul;ltion
dr
=
20A;
d11c to the ;~bscnce of
flow
within
i1
projjlc
is
rct;lincci aftcr conlbrm;ll 1lltlppiIIg.
At
illfinity
in
thc
image
planc,
/If-
induces the poriphcral
I
vclocitics
T
wA:/r.
t
pilcli. Notc:
AT
appean
2w
in thc tcxt with the oppositc sense
of
rotation.
In
this figure, the rotor turns in
a
sense
opposite to that in the text.
'.
OW
--
wA;/t
Tile conservation of ci:culation in conformal n~apping gives
4
1,
(S)
rlS
=
$
;r
(s)
cis,
where
S
denotes the arc of the contour in the flow plane and
s
that in the itnage plane.
The velocities
~nduccd by the bound vortex element
7
(s)ds
in the image plane result from
(6.2--
9)
and
(6.2-
10).
With respect to the velocity components
MJ,,
(z),
\V,,~(Z)
due to
the
deficit of r-t.lnti;s
eddy
within the contour,
the
whirl velocity
-
wri/r,
due to rotation,
anti
the ut!disturhcd velocity components
IV,,
and
11%
cot
fim
in the
x
and y-direction, the
componeilts
of
thz rclativc velocity
in
the itnage plane become
Tilt.
I:ir.etn:itic. boundary condition at
a
station
z,
on
the contour, which makes there
an
angle
//,
..vi~i:
tlx
?-coordinate, rearis
The
angle
/I7
of th.: untlisturbed relative flow with the circumference
is
rather
irnprac?icab!e and can be expressed
by
the more convenient known angle
/3,
of relative
intlux vvith the negative y-axis, as follows
.
1
oA:
or,
cotpx=cotfil
+-§y(s)ds--
+-.
2
t
lV,"
t
\Vm
M',,,
This relation results froin the known limit of the velocity con~ponents in the station
1
at
rc!nr Inlet,
wh=n
this
is
imagined to be at infinity before the rotor cascade
(w,,
=
w,,,),
1
.
o
A:
=
w,,~
cot
pm
-
-
(p
y(s) (1s
+
--
-
or,,
.
2t
t
anc!
rc;,
=
jr;,,
cot
/{,
.
With
the
abbreviation
,
and
~11th repard
tc
(6.3-
1
I),
inserting the velocity components
(6.3-8),
(6.3-9)
into
the:
kinematic boundary condition
(6.3-
lo),
yields the following linear integral equation
for;
the contour velocity
\tv(s)
of the image plane
t
-
222

i
to
A'
w,,
(zp)
2t
+
cot
lj(z,.)
-
cot
p,
+
wrl
[(t)'
-
I]
+
;;;;
-
--
2
w,,,
")nl
I
The
term
o
A:
contains in
A:
the projection of the vane trace
in
the real flow face onto
,
plane normal to the axis.
See
also (5.2-37).
It
follows from the absence of vortex flux
due
to the relative eddy in the interior of the vane and inay be understood as the
eripherally orientated velocity induced at infinity before and behind the cascade by a
P.
strg~ght row of such "eddy-deficit-vortices" each having circulation
2
co
:1:
(Fig. 6.3.2).
After the solution of (6.3-13)
e.g.,
by
means of the conversion of the integr-1
a
into
'
a sum
and hence a conversion into a system of linear equations for the determination of :he
velocity
w(s)
(Cap. 6.2.1.2), the obtained velocities have to be divided by the
scale factor from (6.3-2) to obtain the real contour velocity.
6.3.4.
Cascade
in an axisymmetric
flcw
lamina
of
variable
depth
Consider an axisymmetric flow lamina of variable depth
h
(Fig. 6.3.3 a) passing a circular
cascade. Here the mean streamface with its vane traces
call be transformed into
a
straight
cascade by conformal mapping (Cap. 6.3.1). The velocity scale after (6.3-2) postulates
retaining the layer's
dept!i due to corresponding points in the real and the image face.
Hence
the gradient of the depth
h
in the meridional direction appears as a new parameters
of
the im:~ge plane:
dbldx
=
b'.
In
such a wedged-formed flow lamina the individual bound vortex may be irnazined to
be
normal to the mean stream face. On the faces, covering this lamina, the flow, due to
a
straight elementary vortex partly penetrates these faces and thus is no longer
compatible with the kinematic boundary condition.
Therefore instead of straight elementary vortices the elementary bound vortex now has
to
be
a
ring vortex, that penetrates normal through the co~ering faces
(Fi:.
6.3.3 b).
Since the flow field induced by a ring vortex differs greatly from that of a straight one,
the
influence functions
I;,
fy
(6.2-6), (6.2-7) due to the straight vortex rovi must
be
replaced by corresponding functions due to a row of ring vortices
[5.5].
I
I
f'
Fig.
6.3.3.
Cascade
flow
in a layer
of
varying depth. a) Axi-
symmetric
flow lamina
of
varying depth
b
in a real
X,
Y-flow
plane
and
its image in
a
cylindrical
x,
y-plane,
developable
Onto a plane.
b)
Substitution of
a
straight bound elc~nentary
vortex by an elementary ring vortex.
V=
flow
within the
layer.
/
9
z
i;
Fig.
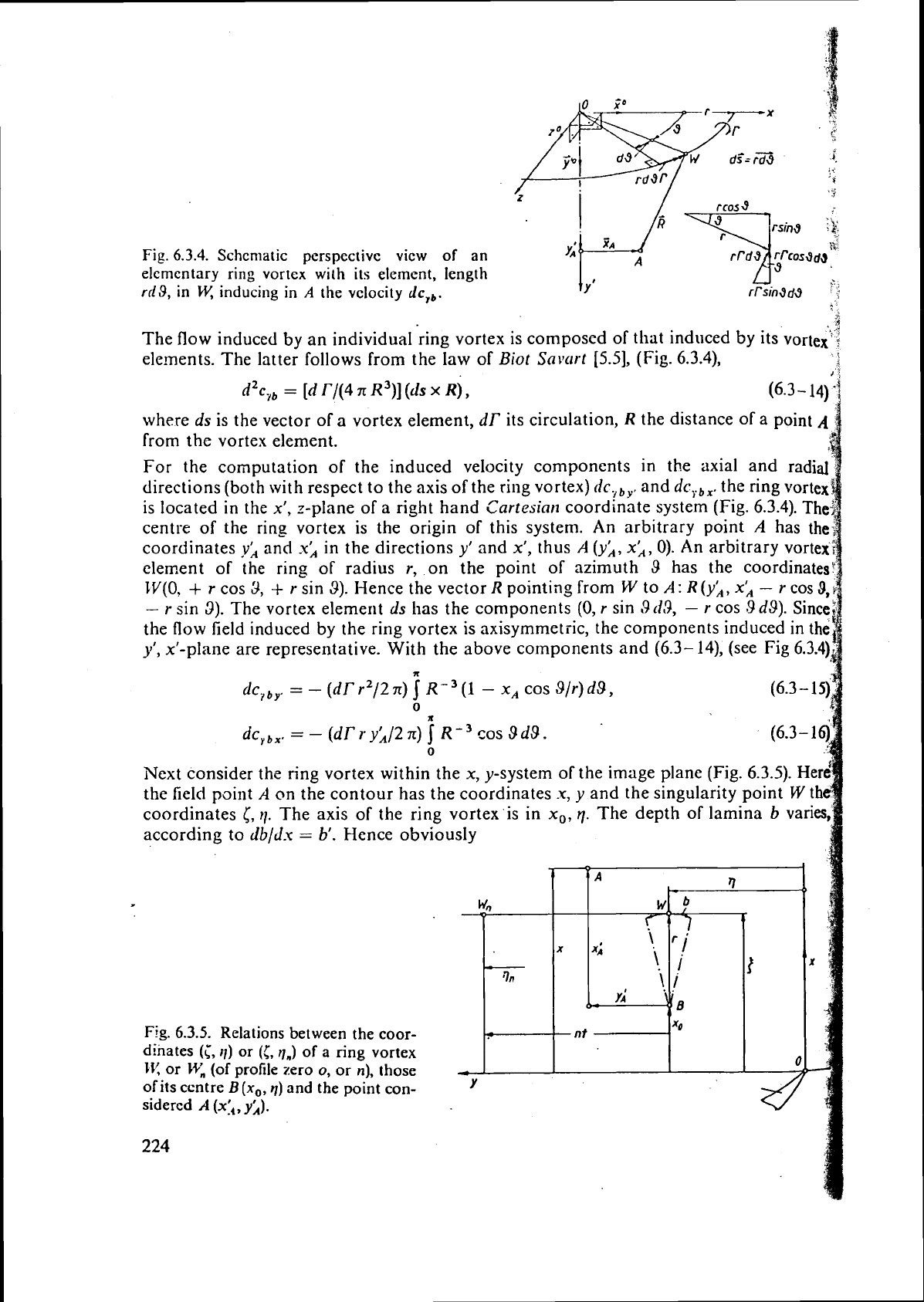
6.3.4.
Schcniatic perspective vicw of an
elementary ring vortex with its element, length
rd9,
in
W,
inducing in
A
the velocity
dc,,.
,n:
The flow induced by an individual ring vortex is composed of that induced by its vortex'
elements. The latter follows from the law of
Biot
Savart [5.5],
(Fig.
6.3.4),
f
C,
d2c,,
=
[d
r/(4
n
R~)]
(Js
x
R)
,
(6.3
-
14)
3
d
where ds is the vector of a vortex element,
dT
its circulation,
R
the distance of a point
A
from the vortex element.
For the computation of the induced velocity components in the axial and
radial
directions (both with respect to the axis of the ring vortex)
dc,,,.
and
dc,.,,.
the ring vortex
is located in the
x',
z-plane of a right hand Cartesian coordinate system (Fig. 6.3.4). The
centre of the ring vortex is the origin of this system. An arbitrary point
A
has the
coordinates
y;
and
x;
in the directions y' and x', thus
A
(y;, x;,
0).
An arbitrary vortex
clement of the ring of radius r, on the point of azimuth
9
has the coordinates
JV(0,
+
r
cos
3,
+
r sin
3).
Hence the vector
R
pointing from
W
to
A:
R
(y;, x:
-
r cos
9,
-
r
sin
3).
The vortex element
ds
has the components (0, r sin
9d3,
-
r
cos
.9
d9). Since
the flow field induced by the ring vortex is axisymmetiic, the components induced
in
the
y',
x'-plane are representative. With the above components and (6.3- 14), (see
Fig
6.3.4)
R
dc,,,,.
=
-
(drr2/2n)
j
R-3(l
-
x, cos 9/r)d9, (6.3-15
0
R
dcYbx.
=
-
(df ryX/2n)
R-3
sos 9d9.
0
Next consider the ring vortex within the
x,
y-system of the image plane (Fig. 6.3.5).
Her
the field point
A
on the contour has the coordinates
.u,
y
and the singularity point
W
t
coordinates
(,
q.
The axis of the ring vortex is in x,,
q.
The depth of lamina
b
vari
according to
db/d.u
=
b'.
Hence obviously
Fig.
6.3.5.
Relations between the coor-
dinates
(i,
11)
or
((,
q.)
of a
ring
vortex
ti:
or
Wn
(of profile zero
o,
or
n),
those
of its
ccntre
BIx,,
rl)
and the point con-
!
.
".
..
ridercd
A
(xl,,
y;).
224

ob\liously (Fig.
6.3.5)
the
coordinates
x',,
y>
of the point
A
in the system
\\lit11
origin in
the centre of the ring vortex can be related to the coordinates
.Y,
y
or
the
point
f
in ths
image plane and to the corresponding coordinates
5,
of
the bound elementary vortex
1V
by
,
x'"
=
x
-
x0
=
x
-
+
bib',
(6.3-
19)
placing the origin of the
x,
y-system
at
the sharp rearward edge of the zero profile. the
co~rdinates
t,,,
11,
of
a
point
IIV,
on the nth profile, which is shifted in y-direction
by
11
r
.
the analogous point
W(t,
11)
on the zero profile are assigned to
<,
11
by
tn
=
5
and
'1.
=
q
+
n
t.
J-Ience for the
nth
profile
x'""
=
x',,
,
y>,,
=
y
-
q
-
nt.
Like
(6.2-4), (6.2'-5)
the
components
of the velocity induced by a straizht
row
of
elementary
ring vortices
with
circulation
dl'
=
y
(s)ds
may be expressed
by
influence
~unctions~,,
fby
accordi!lg to
With the simplifications
by
means of the complete elliptic integrals
E(n/2,
k)
and
F(n/2,
k)
of the
first
and
seccnd
order
[6.16],
defined by
I
and
using the elliptic integrals
I,
(n)
=
j
(a
-
f
cos
9)-312
dg,
0
x
I,
(n)
=
I
(1
-
cos
9)
(a
-
f
cos
9)-
'I2
d9,
0
depending on
E(n/2,
k)
and
F(n/2,
k)
by
11
(n)
=
s
E
(n/2, k);
I3
(n)
=
1
[F
(nj2,
k)
-
E
(n/2,
k)]
,
(6.3
-
26)
the
influence functions
fb,,fb,
can be expressed by

ll'hcn c;llcr~l;ltirl~
the
sirrns, allc~ltioll
113s
to bc ~xlid
10
iIIc
klc.!.
1;1;11
(IIC
illlcger
II
cxiStS
in the term
/I,
tvhich thcr~ inllucrlccs ;11so
11:c
cllip~ic il~tcgrals. I!su;llly
h'
=
tlh/J.\:
<
0-
Cor~cIi~ditlg
rc111;1rk
;~hoi~t stc;~dy
no\\.
ill
C;ISC:I;~~S:
In
11:c
foregoing
.scc.tit~~~s
the
hound
vorliccs
llnvc
bccn assumed
to
hc
oricntatcd
tlornl:~l
to
the
stream
I;ICC.
Whcn
tl~c
hori!~il
vnrlcx
(;111tl
hence
tile cdgc
of
;I
v;lnc)
~ll;tkcs
a11 ;II-bitrary angle
with
;I
yct
;~~isyrnrnc~ric;lll!: ;~ssunicd strcalnbcc,
the
vortex car1 bc
split
into a component nor~n;ll to
thc
s1rc;lrn face :111d ;tllothcr t;~ngcntial to
it.
The tangential component again c;ln be
split
inlo
n
nlcriclic)ll;~l
;lnd
,I
pcripher,ll
onc.
!low
field
due
to
the
lnttcr
corresponds to
that
of
vortc\
rinp
CO;IXI:I~
10
the
n~;icl~i~lc.
-The
field
of
the
me-
ridion:~l comporlcnt twists
thc
axisynlmclric strc;lm
!':ice
within
tllc
\:lnc
clia~~ncls,
sec
;~lso Cap.
10.6.
The axisyrnmctric flow through
a
rcitor clui bc obtitincd
,~lsc,
by
other
nicthotls. S~~/iilling uses
a
streamfunction for
a
laycr of varyirlg
tlcpth
[6.17].
similnr
Cap.
5.7.
1;orc.l
(6.
IS]
applizs potential
theory to
calculate
the flow through gi~idc vanes
and
rotor
in
a
misctl
Ilow
machine. Hirsch
[6.1g]
uses the
finiic
clcrnent method for axisynlrnetric flow
in
turbo~nuchines.
k~*c.L
[6.20],
tl01lc.r
[6.21],
and
Pfoertrter
(6.221.
apply this method
for
a quasi
3
dimensional
flow
\i
it11
tllc
:lit1
of
mcasurcments,
.21(1rtrl!i
[6.23]
uses the finite element method for thc bl:~r.tc to bl:tde
flo\v
c:~lcr~lntion. iZf~rrcri
[6.24]
limits
his consideration on
a
mcan llow plane. Dui,yt!ii
[6.25]
consicicrs
only
upstream
effects.
and
11llber.g
present
n
simplified flow calculation for thc cntrancc of radial
arid
lnixecl flow impellers
[6.26].
5.4.
The
unsteady
flow
throug!~ straight
cascades
in
tandem
arrangement,
moving
relative
to
each
othcr
6,
6.4.1.
Introduction
,
.
The flow past a cascade is pitch periodical and hence that through
:t
c:lscittle past another.
alld
moving re!ative to another is ul~ste:icly.
This
case esists nsually in hydro
'
turbomachines ivith
a
vaned stationary gate nil:{ the runner do\snstream. Hence vane
P
~scillati~ns, :heir fatipue problems, energy loss
tluc
to unstrady circulation and trailing
:
vortex sheet due to it, falsified
measurements
of non-dynamicill probes, are the conse-
quences the engineer is confronted with.
6.4.2.
hlodel
of
cascade
and
assumptiorls
The
flow
in hydraulic turbomachiacs
with
its casc:tdes
of
blrtdcs
in
series moving relati
to anothe:
(as
represented
by
wicket gates and runner blades) is u11ste:tdy. This holds als
for the plane potential
flow
of an ideal fluid. As a model consider the phenonlena withi
two
straight cascades moving relative to each other as shown in Fig.
6.4.1
a. As shown
i
Fig.
6.4.1
b assume the active cascade
'a'
as !ocated :~lterna!i\cly upstream or downstre
of
the passive cascade
'p'.
The active cascade is
the
onc which acts on the passive casca
'p'.
Following
M.
Lot= these assumptions are made (see also
[6.27;
6.281):
1.
Steady flow throush the active cascade.
2.
Location of bound vortices for the profiles of the passive
cascade
alor,g ihe sectio
-
1
<
x,
<
+
1
on a blade
cf
iengtii
2
according to Fig.
6.4.1
b.
The direction of
coincides with
the undisturbed tliroughflow veloci:;~
\r.,
.
(Possihlc in consequence oft
srnrill
angle of attack.)
b,
Some srctlons
of
thtb
bubc'liapter
~:IVC
bccn
published
In
thc proceed~ngs
of
the
ASML'.,
see
[6.27].
publishers
nrz
th.~~~hc.d
I'or
grnnting
perrnisslon
lo
use
them
here.
226
