Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment
Подождите немного. Документ загружается.


6.5.5.
Lir~car differentia! cq~~ation for
Ihc
c,
distribution
lnilially
(6.5--4)
is reduccd to
c,,,
wr
and
/1',
by applying the relation
from the velocity triangle. In addition the identity
I
+
cot2
/j
=
1/sin2
/?
is employed.
under thc assulnption of
a
non vanishing meridional vclocity c,,, (6.5--4) is di\.ided
b\-
,m/sin2
/l.
Finally the varinblcs are made dimensionless by
y
=
c,/c,,
(with c,,
=
c,,,
(,I
=
0))
,
x
=
n/b
,
(6.5
-
6)
b
being the local span (breadth) of the runner in the n-direction. Hence the 2n\.erning
differential e.quation for the
y
(x)
distribution
j2
(x)
=
(h o/cn,,) sin 2
fl
sin 11,
(6.5-
S)
fl
(x)
=
(h/R) sin2
P
-
(b/r)
cos2
P
sin
11
4-
(112) sin
2
Pd(cot P)/ds
+
[C
hl(4 AII)] {tan p/sin
fl
-
tan p1 (sin2 P/sin3
p,)
[r
A~li(r.,
.4?1,
)I2:
.
(6.5-9)
A
related proble~n is the influence of a meridional profile of a mixed flow machifie on its
characteristics, see
[6.40].
6.5.6.
Step
by
step soiotic~n for the design task
Transforming (6.5-
7)
into
a
difference equation and puttins
fl
(s)
-
fl
and
ji
(s)
-
.f,
yields the increment
Ay,
j9
experiences,
when
a
step Ax is made in the
.Y-cliscction.
b>z
means of
AY
=
-
Ax(S,
Y
+f2).
i6.5-
10)
On
the shroud, i.e.,
y
=
I,
due to
c,(n
=
0)
=
c,,,
the value
c
,,,,
is set with respect to
a
limit of susceptibility to cavitation. This holds especially for points close to
the
exit
I.
In
a design usually the flow rate
Q
is prescribed. Hcnce this procedure is finished, when
according to continuity, with a mean contraction coeficient
(I,
at the station x
=
1,
with
c,,,
h prelinlinarily chosen,
Q
reaches the set value. C'suall!.,
because b is unknown in
a
design, the latter value of
Q
will be attained
by
an
x
differing
from 1. This then gives the breadth
b
required for the flow
Q.
6.5.7.
Calctllating
c,
(n)
or
y(x)
for a runner
of
given
geonletry
under
a given
flow
rate
Q
The origin;llly posed task asks for the
cn,(n)
or y(x) distribution in
a
runner
with
knoivn
hand
geornctry (hence
/?,
p,
are known as functions of x). For this purpose a prelimirlary
plot of streamlines
has
to
be made, with provisionally plotted 2;-lines normal
to
them.
Thus
8,
R,
r, are known preliminarily as function of
x
2nd
tllrn also
Jl
and
j2
are
Provisionally known and then stepwisely improved.
237

I-lcrc also t!ic procctiurc' of
Cap.
6.5.6 may bc nppliccl with the cliffcrencc, that now by
trial
and
error
(a,,,
Iias
to
hc
set so as
lo
satisfy continuity
(5.5-
11).
Whcn
the
f~~nctiolis
/',
and
J,
arc grapliicr~ily givcn or
expressed
in terms of
s,
then
gr:!pliical or n~i~iic~-ic;~l i~itegratio~i niay facilitate obtaining
y
by nleans of the following
strict solution
of
(6.5-7)
given by thc author
[5.39]
6.5.8.
Computation
of
P
as
a
function of
vanc
georrietry
The
inclination
fi
of relative flow with respect to the circumference follows from the angle
/?'
bctwcen the pattern section of the vane and the periphery, the angle
O
of the radial
vane section with the radius and the incliliation
p
of the meridion~ll streamline with the
radius as
tan
fi
=
tan
pl
sin @/sin
(O
+
~i).
(6.5- 13)
Ttlis results from an
infinitesimally
small tetrahedron (Fig. 6.5.1 c). It is formed by two
rectangular triangles, one parallel to the
plan and another in the axisymmetric stream-
face,
aild
by
two common triangles, one located in the vane kce and the other in the
meridian. The peripherally oriented leg, which is common to both rectangular triangles,
rrtight has.e
unit
lr:ngth. From this the length of the meridional streamline element is
obtained us
ta:l
and
that of the radial oriented edge as tan
pl.
It is realized from the
~rir~ngle within the rneridirtn, that the angles
rc
-
(O
+
p)
and
O
are opposite the legs
hacing the length tan
/j'
and tan
b.
Fs-m this
a
basic trigonometric relation yields
(6.5-
13j.
.i
6
6.6.
The
siip
effect
in
the
flow
past
a
rotor
a
6.6.1.
Introduction
For the blading of a certain fluid machine, specific head
gH,
flow
Q,
speed
u
and henc
also size
D
being known, an estimate of efficiency
rl,
(resulting from internal flow) and th
change
of
whirl
cui
by the rotor, between the stations
1
and
2
(see 5.3) from
Euler's
relatio
are of importance.
As the
v:hirl
cUi
due to rotor's influx is either physically give11 e.g.,
c,,
=
0
in pumps,
adjustable
e.g., b:; gates of turbines, special attention merits the whirl past the rotor
exi
Hence the problem is limited to impellers. They have a low vane number
z
and thus
relalive nlr~in
floiv.
disordered by secondary flow (Cap. 5-51, and hence no longer fo
ins
thz
vane. At exit
2
the latter makes an angle
/?;
with the periphery. Now the pro
ariscs, :o set
/3;
so
as
to generate
the
whiri, required for the head from
c,,
=
yH/(q,
rz
and thereby also needed for a desired flow
Q
(Fig.
6.6.1
a).
Ob\iously (Fig. 6.6.1
a)
there is a discrepancy between the velocity triangles at station
one of which is due to the pitch-averaged flow and thus also due to
E:tler9s
relation
the other
of
which, denoted by
a
star
*,
is due to a relative flow along the impeller
v
plotted for the same rneridional velocity
c,,
=
c:,
.
238
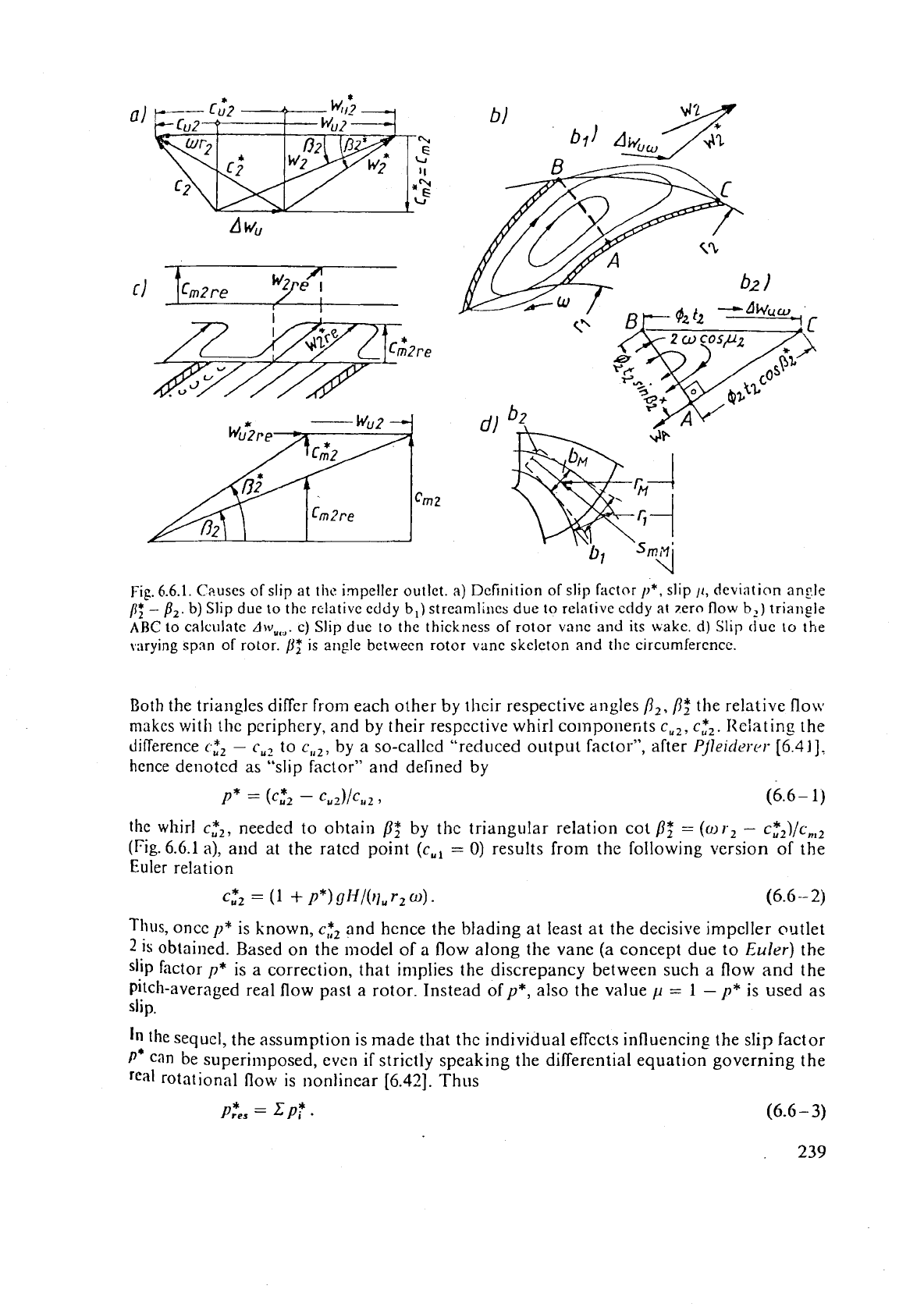
Fig.
6.6.1.
Causes of slip
at
thc impeller outlet.
a)
Definition of slip factor
p*,
slip
11,
deviation angle
-
/Iz.
b) Slip due
to
the rc-lative
cddy
b,)
streamlines due to relarive cddy
at
7ero flow
h,)
triangle
ARC
to
calculate
AW,~,.
c) Slip
due
to the thickness of rotor
vanc and
its wake. d) Sl~p
tiuc
to the
varying span of rotor.
,Of
is angle bctwecn rotor vanc skeleton and the circurnfercnce.
Both the triangles differ from each other by thcir respective angles
/I,,
/?:
the relative
flow
makes with thc pcriphcry, and by their respcctive whirl componerits c,,, c:,. Ixclating the
difference
c,*,
-
cU2
to c,,,, by a so-callcd "reduced output factor", after
P'1eidrrc~1-
[6.41].
hcnce denotcd as "slip factor" and defined by
the
whirl c$, needed to obtain
fiT
by thc triangular relation cot
Pt
=
(wr,
-
c,*,)lc,,,
(Fig.
6.6.1
a), and at the ratcd point
(c,,
=
0)
results from the following version of the
Euler relation
c,*2
=
(1
+
P*)
gH/(Vu
r2
(4
-
(6.6
--
2)
Thus,
oncc
p*
is known, c2 and hcnce the blading at least at the decisive impeller outlet
2
is obtained. Based on the model of a
flow
along the vane (a concept due to
Euler)
the
slip factor
p*
is a correction, that iniplies the discrepancy between such a flow and the
pitch-averaged real flow past
a
rotor. Instead of p*, also the value
I(
=
1
-
p*
is used as
slip.
In
the sequel, the assumption is made that thc individual effects influencing the slip factor
P*
can be superimposed, even
if
strictly speaking the differcntial equation governing the
real
rotational flow is nonlinear [6.42]. Thus

Thc followiu_c four
cffccts
arc highlighted as tlic
most
inflttcntial orics on the slip factor:
:I)
I-':
fro~i rot a!iu~i,
b)
11;
from
w;lkcs
and
finite
v;irlc thickness, c)
;lz0
from cascadc flow,
J)
p,*
frorn
vnr>ing
brcadtll
l?
of thc rotor.
6.6.2.
Slip
p:
in
consequence
of
tlic
rclativc
eddy
After Cap.
5.2
the steady relative
flow
of an ideal fluid on axisymmetric strean1 faces under
irrotational absol~~tc flow, can be split into one due to throughflow
(Q)
and another due
to the component
2
(11
cos
11
of the relative eddy normal to the stream face.
Obviously in Fig. 6.6.1 b,, the relative eddy
alone at zero flow
(Q
=
0)
reduces the whirl
C"
,,
to
c,,,.
Hence the pitch-averaged differential whirl component
Alv,,,
=
c,*,
-
cu2 can
be used to predict
p:.
To obtain
d~r.,,,.
by which then
pz
is gained from (6.6-
1)
and c,,,
=
gH/(qUr2
m),
Stokes'
theorem (Cap.
5.2)
is applied to the triangular-like area
ABC
(Fig. 6.6.1 b,). The circula-
tion, then needed, along the unobstructed pitch arc
@,
t2 (@,-contraction coefficient due
lo vane thickness and boundary layer in 2) reads:
$
tu
ds
=
f',
=
dw,,
t,
@,
.
Obviously
--
DL
along the line
BA
the circulation vanishes. Hence
TEA
=
0.
With the hint (Cap. 5.2)
applied to an impeller where approximately
MI,
=
or,,
the velocity at station
A
in
consequence of the relative eddy alone becomes
w,
=
t,
@,
(11
sin
/?T
cos
p,
[l
-
r,/(2 r2)].
(6.6
-
4)
When the passage of the channel is assumed to be closed, for the case of vanishing
flow
(2,
the flow then induced by the relative eddy on the outstanding corner
C
has to vanish.
Assume that the relative flow drops from
A
to
C,
distance
t,
Q2
cos
/?T,
so as to make the
circulation along
CA:
T,,
=
(w,/2)
t,
@,
cos
1;.
The vortex
flux
due to the relative eddy, passing the triangular arca, becomes
Jl
rot
wdA
-
CJ
cos
pz
4;
t:
cos
/I;
sin
/IT.
Making this equal to the circulation about the triangle
'1BC:
r,,
+
Ii,
i-
c,,
Stokes'
theorem (Cap. 5.2) thus yields [6.45]
Aw,,
=
7t
@,
or, sin 2PT
cos
p2
[l
+
r1/(2r2)]/(2z).
(6.6
-
5)
tlence from
(6.6-
1)
with c,,
=
gH/(qur20) and applying the blade tip speed coefficient
Klr
(Cap.
9.2j,
p:
reads
pz
=
(n
Kz12/z)
q,
@,
sin 2
PT
cos
p2[1
+
r1/(2
r,)]
.
6.6.3.
Slip
pl
as
a
consequence
of
wakes
L
A
wake
usanlly exists past an impeller vane. This contracts the main relative flow by the-,
contraction coefficient
~5~.
Assume that the wake is extinct at a station 2 (Fig. 6.6.1
c).
downstream of the exit. Assuming straight and plane flow, continuity requires between
the real
meridionai components cm2
.,
at station 2 and czZre at station 2* (exit)
3
8
Irnazine between
2
and 2* vanishing peripheral forces on the
flow,
then the momentum;/
theorem requires
bv,
,
,,
=
~y:~
,,
for the straight cascade now considered. The subscript
re holds for the real
flow at
2
and
2*.
By definition (6.6.-
1)
the slip factor
p*
results fromT:
d

,he comparison of the velccity trianglcs
31
2 and 2*, having the same n~eridional com-
P
onc~lt.
?'his gives the slip (Fig. 6.6.1 c)
c,*,
-
cU2
=
c,,
(I/@,
-
1)
CO~
Pf
,
(6.6
-
8)
and by mcans of (6.6- 1
j
the desired slip factor
pl
=
2
cp2
Ku2
q,cot
PZ
(1/Q2
-
I),
(6.6
-
9)
,&ere
9,
=
c,,/u, is the flow coefficient (Cap.
9.2).
6.6.4.
Slip
p4
as
a
consequence
of
cascade
flow
The special influence the cascade of
a
mixed flow rotor has on the slip is that due to the
eddy, as treated above. Under the assumption that the individual slip
ef?-ects can
be
superimposed, the remaining effects due to a cascade will be studied at a stationary
cascade with plane potential flow on axisymmetric stream faces. After Cap. 6.2.1 this can
be
transformed into a straight cascade at angles retained by conformal mapping.
Therefore imagine the cascade of the impeller considered to be thus transformed into a
cascade. Retaining
the angles
/IT,
/I2
under this procedure means also retailling
the so-called "deviation angle"
,!IT
-
/I2
(Fig. 6.6.1 a) due to the s!ip
c,*,
-
c,, ar?d linked
to it by the obvious relation
Hence the slip factor from
(6.6-
I)
is linked to the deviation anglc (remember alvays
in
the case of pumps) by means of
As
will be seen in the following, the deviation angle
/J;
-
/3,
can be easily obtai!~ed for
a
cascade of given geometry and within a certain undisturbed flow
lv,
(a~d the conse-
quent physical angle of attack
6,)
by mcans of cascade theory according to
Cap.
6.2.
The conformal mapping of a usual radial or mixed flow impeller with its small vane
angles
results in a straight cascade, having
a
pitch to chord ratio
t/L
smaller than "one"
(tjL
<
1).
-
Consideration of the deviation angle
/If
-
/I,
at the outlet of a straight cascade lvith
tlL<
1,
vane angle
/IT
at exit
2
known: For this purpose some findings of the cascade flow
in Cap.
6.2
and Cap. 6.3 must be reviewed.
First the lift coefficient
c,,
of an aerofoil within a cascade is linked to its pitch
to
chord
ratio
t/L,
the so-called "deflection" Ac,
=
c,,
-
c,,, and the undisturbed throughflow
velocity
wco
by the relation
(6.3--4)
Obviously
as
in Fig.
5.5.5
d,
the so-called "deflection triangle", extracted from both the
velocity
trianglcs, and consisting of Ac,,
w,,
w,
and hence also
w,
=
(w,
+
N*,);Z,
yields
Acy
=
c,(cot
P1
-
cot
P2).
(6.6
-
13)
On the othcr hand the same
lift
coeflicient
follows, according to cascade theory frorn
(6.2-50).
Substituting there for
thc
physical angle of attack
6,
the difference of the i~nele
PO,
between zero Lift direction and the
circumference,
and the angle
8,,
the undisturbed
velocity
wr
11l;lLcs will1 ihc circumft~r~nce. ;~crordin~ to
d,
=
/I,
-
11,. and substituting
for
0,
the 11101-c
L',Y;IC~
cxprt:ssio~l sin
do,
the relation (6.2-50) rcads
[A
=
2
n
;r
sin
(11,
-
/I,,),
(6.6
-
14)
where
ir
tlic casc:~dc factor, after (6.2-45), is
n
~nerc fi~nction of ihe cascade paranlcters
t/L
and
11,.
Elimiiinting
c,,,
from (6.6.-
14)
and (6.6-13), ncccunting for the relation
sin
p,
=
c,,,/w,
from thc vclocity trianglc and iogethcr with the known theorern
sin (Po
-
/I(,,)
=
sin /I, cos
/II,
-
cos lJO sin
,!I,,
brings
2q(cot
/I,
-
cot
/I,)
=
(cot
8,
-
cot p,),
(6.6-
15)
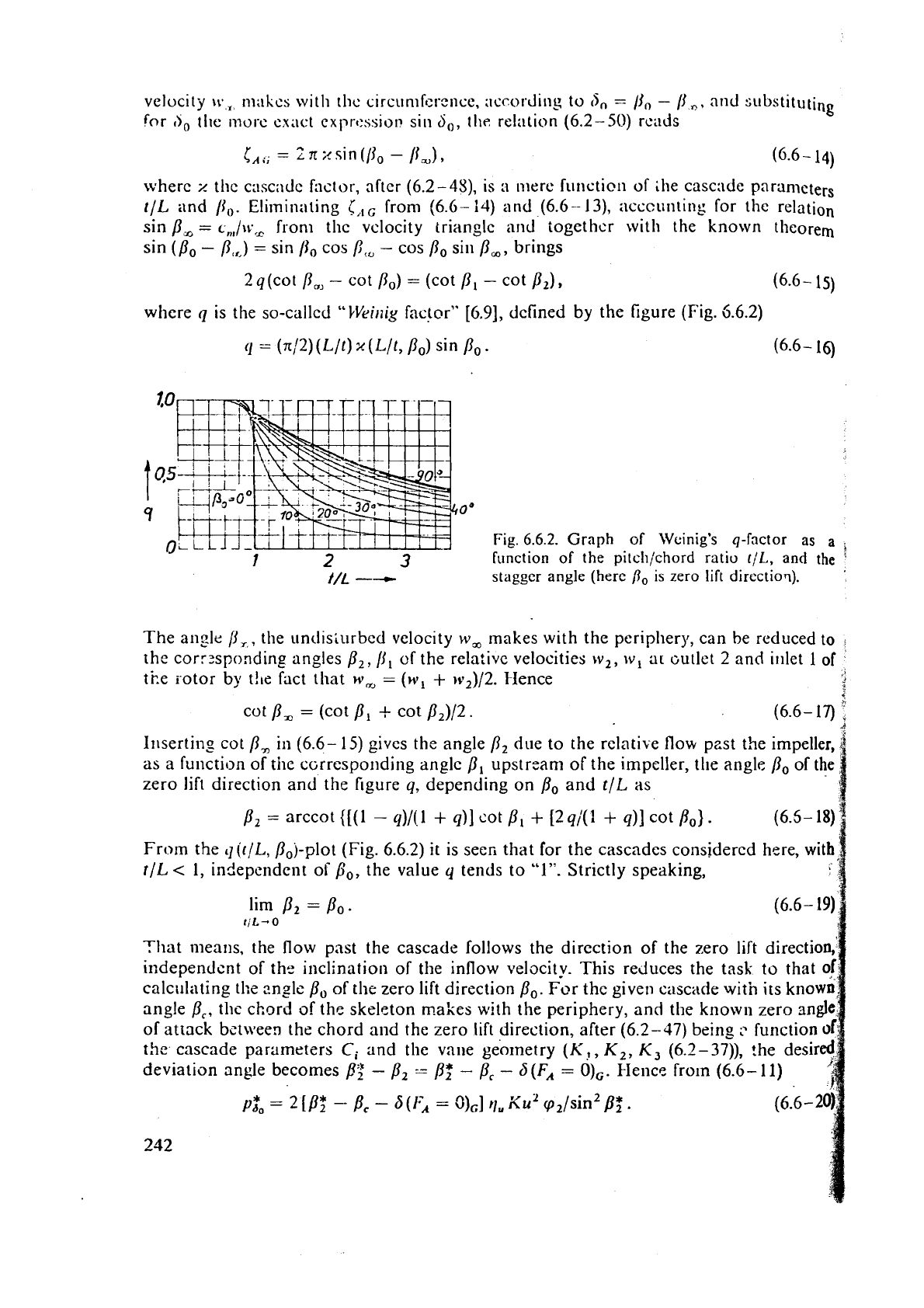
where
q
is the so-called
"kVri~liy
factor" [6.9], defined by the figure (Fig. 5.6.2)
(1
=
(n/2) (Llt)
x
(Llt, Do) sin
Po.
(6.6-
16)
la5
9
0"
Fig.
6.6.2.
Graph
~f
Wcinig's
q-factor
as
a
,
2
3
function
of
the
pitch/chord ratio
f/L,
and
the
"
I/L
--
stagger
angle
(here
/3,
is zero lift directioq).
The
angle
/I,,
the undisiurbed velocity
tv,
makes with the periphery, can be reduced to
.
thc
corr3sponding angles
P,,
I,',
of the
relative
velocities rv,,
w,
ar ~utlet 2 and illlet 1 of
the rotor by t!~e fact that
w,
=
(w,
+
1v2)/2. Hence
J
i
cot
p,
=
(cot
p,
-t
cot p2)/2.
(6.6- 17)
*
f
I~~sertinp cot
8,
in (6.6- 15) gives the angle
/?,
due to the relatike flow pzst the impeller,
as
a function of the c~rrespollding anglc
P,
upstream
of
the impeller, the angle
Po
of the
zero lift direction and the figure
q,
depending on
Po
and t/L as
From the
qit/L, P,j-plot (Fig. 6.6.2) it is seen that for the cascades considered here, with
r/L
<
1,
independent or
bO,
the value
q
tends to "1''. Strictly speaking,
lim
p2
=
Po.
(6.6-
19)
t,L--0
That inealls,
the
flow past the cascade follows the direction of the zero lift direction,
independcnt of tht. inclination of the inflow velocity. This reduces the task- to that
of
calcillating t1:e mgle
Po
of the zero lift direction
8,.
For
the given cascade with its known
angle
PC, thc chord
of
the skeleton makes with the periphery, and the known zero angle
of
attack bztween the chord and the zero lift direction, after (6.2-47) being
r-
function
of
the cascade parameters
Ci
and the valie geometry
(K!
,
K,,
K,
(6.2-37)), !he desired
deviation angle becomes
,!?:
-
P2
-h
B:
-
PC
-
8(FA
=
O),.
Hence from
(6.6-
11)

6.6.5
Slip
pt
3s
a
consequelice
of
varying
the
breadth
of
the
rotor
I\
conical strea~nktce is considered (Fig. 6.6.1 dl, touching the nlcan stresm face of the
flow
lamina considered in the middle of the impeller. Imagine this conical L:ce to be the mean
face
of
a
flow
lamina with the same depth 'b' of the actual lamina at stations. whose
distance, from the point of contact
x
within the meridian (Fig. 6.6.1 d) is the same along
the
straight generatrix of the COile as along the curved line on the original mean stream
face of the flour lamina considered.
depth b is assumed as
small compared with the distance
r
from the axis. Using the
nleridional coordiliate s, along the generatrix and the azimuth cp', normal to the meridian
(Fig. 6.6.1 d), conti~~uity due to an axisymmetrical flow within the flow lamina can be
\\fitten down
as
(<p'
being the angle between generatrices with in the cone plane)
awn,ic7srn
+
w,/s,
+
(1
IS,)
~w,Ic~~~
=
-
(~,,/b) db!nsm,
(6.6-21)
IV,
is the meridional component,
w,
the whirl component
of
flow. Hence the effect
of
varying depth b
=
b(s,) of the flow lamina can be interpreted as that of
a
source-
distribution
-
(\v,/b)(db/ris,,) due to a plane flow within the
s,,
cpl-face.
~ssuming for simplicity
w,,
on the right hand side to be constant over the pitch and to
match
the
pitch-avcraged mc'ridional speed due to the given flow
Q,
an additional whirl
component is generated at impeller exit
2
as compared with that, due to
a
rotor with
constant breadth
b
(Fig. 6.6.1 d)
b,
and
h2 being the breadths at station
I
and
2
of the real ele~ncntary pump
or
\~~holc
pump (as the case may be). Making
Aw,,
=
Ac,,
=
c,r2
-
cU2, this implies a slip kctor
The slip factor has been ge~~erally treated by
Adler
[6.4],
and in connection with pump-turbixs
by
Arttot1
[6.43].
Recently
3-dimensional
mcasurcments
of
the relntivc flow field
in
the channcls and
past
Fig.
6.6.3.
Values
of
slip
factor
p
=
I
-
p*
obtained
by
several
authors.
a)
-
K
orcian
[6.44],
---
Raabe
[6.45],
---
Siehrechr
[6.47],
1
/
1
/
vciderer
[6.4
I],
._.
Stephanofl
[6.48],
-.-
Stodola
[6.49],
-. . ._
Pfoertner
[6.22],
..
. .
Busenznnn
[6,50],
o
Eck
16.511,
x
x
Noorbakhslt
16.521,
b)
-
Korcian
16.44],
-
-
-
Murokanli
[6.53],
.-
-
OslerwalJer, E~tig (6.541.

2
I
9-
4,
a
r;ldi;~I
pump
inipcllcr. cnrr~cci out by
J.
Korcltrrr
at tlic Lch~stuhl i:nd Labor fur
I
lyilraulische
,
blusch~~~cn und Anlagen dcr
l'!;hl
Ih.JJ]
agrcc \tcil
\vi~h
thc slip f:~ctc>rs prcdlctcd by
Rctrlhc.
[6.js1
Thcsc
results
\\crc
;II\o
comp.~rcd
\vitli
rchulib obt:l~ncrl either Krurn tI:corct~c;~I prcdicti~~ls or
test;
carricd out or c;llcill;~tcd
by
Sic.hrt,rlr/
(6.371,
Stc>i~tri~r!g
(6
4S).
S/otloltr
[h.49].
Brr\cnrtrtln
[6.50],
~~k
16.511.
Noo:-h~rA\l~
[6.52],
Al~rrt~lirl~~ri. h'ili~rytrt?rtl
and
~lstrkrrro
[6.53]
;~nd
0.srer~rcrltlc~r
and
Ettig
[6.q
In general, agrccrr~clit was more or less good at the dcsign point but failcd in some cases at part
load
and ovcrlond, see
Fig.
6.6.3.
4
Fig. 6.6.4 shows the rotor with the electrically adjusted 6-port probe used by
Korcian
by
which
pressure anti the spatial rclativc velocity vector wcre mcasi~red simultaneously.
Y
At the moment the pump works under developed cavitation, c.g.
;IS
an inducer, any prediction
ofthe
slip factor fails, since this is based on the assumption of a fully wall-attached and non cavitatine
flow,
The cavitating
flow
through a cascade has bcen treated by
Furlrya
[6.46].
probe adjustment by turning the probe about its shaft and by shifting its shaft in axial directi
4)
mass foi balancing the centrifugal force of the probe and its adjustment device,
5)
covcriilg
pl
for the slide ring of the seal,
6)
radial extension of the shroud,
7)
6-hole probe,
8)
scale ring
indication of the azimuth,
9)
runner,
10)
flange.

7.
Losses
due
to
vorticity
and
boundary
layers
7.1.
Introduction
An)'
real flow in fluid machinery is linked to the formation of vortices, boundary layers.
and \vakes as vortex sheets \vhich are the origin of dissipation and energy waste.
Vortices normal to the main flow may contribute to the circt~lation about
a
vane, vortices
in
the main flow dircction
stimulate
the generation of secondary flow. Hence
understanding the production of strealnwise vorticity
at
the outlet of structural members
of fluid machines, like no7zles, bends, rotors, cascades may help
to
influence
this loss
mechanism.
Once the longitudinal iforticity in the main flow direction is known, the secondary flow
and resulting loss can be predicted.
In
mixed-flow fluid machines the rotor may be the main source of loss. Therefore an
attcmpt is 11ladc to predict the dissipation in its vortex layers such as the boundary layer
;ind
wake.
The latter requires the knowledge both of boundary layer growth in the
main flow
direction along
a
double curved vanc and ;ilso the secontiary
flow
accompanying
it.
An
estimation
of this grou;th is obtained from the momentum equation, continuity and wall
shear stress as functions
of
tl:e flow regime of the boundary layer and its transition points.
It
~ncludes the influer~cc of
Cor.iolis
force and the body force due to thc curvature of
stream1il;es aiong the vane in the directions of the main and secondary flow in planes
tangential
atid 11orrnal to the vane.
It
needs the introduction of a reasonable velocity profile in thc direction of the rnain and
secondary flow. It also has to account for
the flow about the leading edge of the rotor vane
and the effects due to the formation of the wake.
7.2. Yroblcms
due
to kinematics
of
vortices in fluid machines
7.2.1.
Fundamentals
of
vortices
The forced vortices here considered
may
have their origin
in
the core of a free vortex
Generated by the curvature of guide walls. Vortices are mainly caused by means of visco-
sity
in wall-attached boundary layers or wakes with a flow having a large strain rate
across the main flow. According to
the
findings of
Oseen
[7.1]
vortices fade by converting
'heir rotational kinetic energy into waste heat.
In
the following, idealized vortex tubes are imagined to be floating within the main flow
neither subjected to fieat transfer iior
generating
heat.

1-'ig.
i.?.
1.
a)
\'orlox tubo, its dirnc~is;nns.
I))
CJcncration
,f
I~~i~!i~t~cli~i;~I
(SI~L:;IIII~V~SC)
vorficity
R,
i~i
(!lo nozzlc
:
a
''1
\fcrtic;il j>cl~on tt~rbil~o
by
IIIC~\IIS
01
llie mon,ciIt
of
momen-
.
-
tulll
of
fltvv
111
thc
pcnstock
2.
c) Amplification
of
thc
kinctjc
cncrgy
of
t
hc vortex with vorticity
S2,
by :~ccclcration.
Consider
a
straight vostcx tube of length
1
with the momentary constant circular
cross
section of diameter
D.
It
rotates with constani angular velocity
0
about its axis, corre-
spondifig to the vortex intensity curl
c
-
l2
=
20
(Fig.
7.2.1
a).
According to
Me1n:holtz
or
Kelvin
[7.2;
7.31,
the vortex tube consists always or the same
matter.
Assuming constant
dcnsity of fluid
Q,
rnass conservation requires
m
=
Q(Z/~)D*I
=
const, or
D~I=
const.
(7.2-
1)
Accorcling to
Stolies'
theorem (Cap.
5.2),
i
r
=
(44) D'Q
=
const,
or
02Q
=
const.
(7.2-211
Jn an ideal fluid the theorern of the moment of momentum requires
I
=
(~132)
gD4
!to
=
const,
or
D4
10
=
const.
Dividing
(7.2.
-
2)
by
(7.2
-
1)
gives
Qjl
=
20/1
=
Q
r/nl
=
const.
With
(7.2-2')
the kinetic energy of the vortex tube results
in
E
=
(lj2)
(02(rr/32)
QD'I
=
gT21j(16rc)
=
const.
Hence
E
ir~creases by lengthening of a vortex tube.
7.2.2.
Energy
loss
due
to
lengthening
of
a
vortex
tube
7.2.2.1.
Lengthening of
a
vortex
tube
parallel
to the
main
flow
This effcct occurs,
z.g.,
in
the nozzle pipe of
an
impulse turbine
(Fig.
7.2.1
a)
w
main flow has
a
streamwise vorticity. This originates from a free vortex about the
a
of
:he
pipe in connection with the fluid viscosity and a large strain rate there.
Such a whirl usually is effected
by
two bends in series upstream of the nozzles,
both
bei
in
planes that are inclined to each other.
For example
a
multi-nozzle in~pulse turbine with
a
vertical
shaft
(Fig.
7.2.1
b)
has one
of
these
be
in the elevtation, which connects the penstock with the distributing pipe.
The
other bend is
tha
246
