Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment
Подождите немного. Документ загружается.

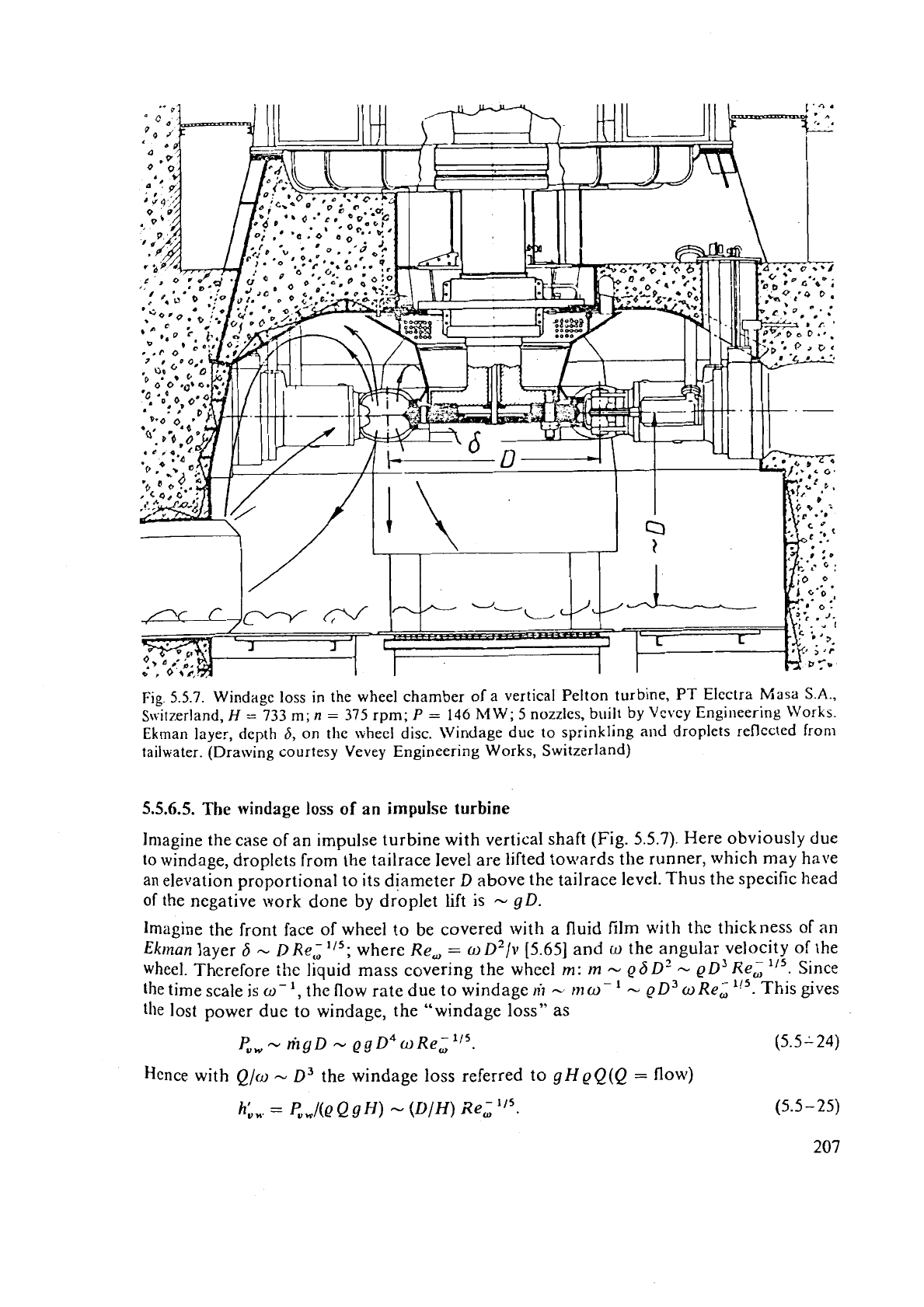
Fig.
5.5.7. Windage loss in the wheel chamber of a vertical Pelton turbine, PT Elcctra Masa
S.A.,
Switzerland,
H
=
733
m;
n
=
375 rpm;
P
=
146
MW;
5
nozzles, built by Vcvey Engineering
Works.
Ekman layer, depth
6,
on the wheel disc. Windage due to sprinkling
and
droplets reflected
from
tailwater. (Drawing courtesy Vevey Engineering Works, Switzerland)
5.5.6.5.
The
windage
loss of
an
impulse
turbine
Imagine the case of an impulse turbine with vertical shaft (Fig. 5.5.7). Here obviously due
to
windage, droplets from the tailrace level are lifted towlards the runner, which may have
an elevation proportional to its diameter
D
above the tailrace level. Thus the specific
head
or
the negative work done by droplet lift is
-
gD.
Imagine the front face of wheel to be covered with a fluid film with the thickness of an
Ekrnan
layer
6
-
D
Re;
'I5;
where
Re,
=
o
D'/V
[5.65]
and
w
the angular velocity of the
wheel. Therefore
ihc
liquid mass covering the whcel
m:
m
-
~6
D'
-
QD~
Re3
'I5.
Since
the
time scale is
o-
',
the flow rate due to windage
--
mo-
'
--
e~3
w
Re;
'I5.
This gives
the lost power due
to
windage, the "windage loss"
as
Hcnce with
Q/OJ
-
D3
the windage loss referred to
g
H
Q
Q(Q
=
flow)

5.5.7.
The
loss
duc
to
cross
flow
on
a
bucket
of
a
YI'
The loss factor
[
of the individual specific losses
may
vary with the
Rcyriolrls
or
Eketah
number
Re
or it may not,
e.g.
draft tube loss. The former, correspoedi~ig to all elliciency
scale eNect, usually rises with
Re,
e.g. loss due to pipe friction, disk friction, windage,
but
sometimes also decreases with rising Re.
The loss due to cross flow on the bucket of a
PT
is an example of the latter. Let
this
motion have velocity
v.
Hence the specific loss
hi,,,
-
V~/(~II).
This cross 110w is Caused
by the pressure incrcase
Ap
across the jet normal to the bucket face. After Pascal's theo.
rem
Ap
acts also tangential to the bucket face. Thus
Aplg
-
u2.
See also Fig.
5.5.8.
Ap
is caused by the centrifugal force
w2/R
of the relative flow with speed
w
in con.
sequence of the curvature
l/R
of the bucket face. Thus with
do
as the jet diameter
3p
--
QW~~,/R.
Hence the loss due to the bucket cross flow with
Kw
=
w/(2gH)'I2
After Raabe
[5.66]
with
1
=
Q/Q,,
as load factor, continuity gives the following relation
3etvreen the jet diameter
do
under arbitrary flow
Q,
and this diameter
do,,
under
(I0,
a1
bep:
do
=
d,,,.
An idealized velocity triangle formed by the velocity coefficient
KH
due to the relative flow,
K
tl
due to wheel speed and
Kc,
=
~,/(2~ 1-1)'~~
due to the jet vel-
ocity at
Q
gives:
K
n9
=
Kc,
-
Ku.
Assuming the loss within the nozzle pipe to follow
thdt of a straight pipe in turbulent flow, then
2
112
Kc
=
(1
-
k
Re-''" K c,)
,
(5.5-27:
in which
k
is the loss coeficient,
Kc,
=
C~/(~~H)'~~,
c,
the speed within the ~ozzle pipe,
diameter
d,.
At bep:
KC,^
Kc,,,
and
Re
=
c,d,/v
-,
Re,,.
With the above load degree
I,
continuity gives
Re
=
RRe,,.
Hence from the above, the approximated loss
Obviously under overload
(1
>
1)
and corresponding to tests,
hicr
increases with rising
Re,,.

6.
Prediction
of
internal
flow
in
cascades
and
rotor
6.1.
Introduction
The steady irrotational flow through
a
straight cascade of aerofoils can be cot~sidered as
a
simple model for the relative flow in axial turbomrtchines. Jt allo~vs the prediction
of
the steady flow outside the boundary layers, which passes such a cascade of
_eiven
gometry and given flow admission (indirect problem.) Jts solution is based on the
singi~larity method, where bound vortices are continuously distributed along the contour
of the profiles.
TIlc resulling linear intcgral equation for the contour velocity can be solved by dividin:
thc
contour into a finite number of elements, which _gives a linear system for this velocity.
The solution of the direct problem, as the task to design a
ce,-tain cascade for given
velocity triangles
call be obtained from that of the indirect problem only by additional
ccnditions.
Neglecting the
finite thickness of profiles the singularity method
can
be simplilicd for the
case of small angles of attack and profiles with small
chamber by distributing thc
singularities on a straight line along the undisturbed velocity kno\vn from the vciocity
triangles.
The results of flow through straight cascades can be used also for the
flojv through mixed
flow gates and rotors by means of conformal mapping,
if
the flow is assumed to be
axisymmetric with respect to the stream faces. The varying thickness of
flow
laminae
requires the introduction of a bound ring vortex.
The concept of
axisymmetric elementary turbines requires information about the distri-
bution of meridional velocity normal to them.
A
simplified estimate of the effects caused
by
finite vane number is given by introducing the slip factor.
A
general survey of the flow in cascades
is
givcrl by
Scholz
[5.13],
fialcpel(6.11,
and
Raabe
16.81.
6.2.
The straight cascade
as
a model for axial
fluid
machines
6.2.1.
Prediction
of
flow
(indirect
problem)
by
means
of
the
method
of
singularities
6.2.1.1.
Introduction, description and theory
of
problem
The steady ideal flow through an axial rotor is desired. This flow is assulned to be on
coaxial cylindrical stream faces.
As
the predominating relative whirl (Cap.
5.2)
here is
Parallel to the rotor axis, the plane
re!ative flow within the cylindrical face, now unrolled
in
a
plane, is
a
plane potential flow.
The
known cylindrical sections of the rotor vane& are

Fig.
6.2.1.
St r;~igIi
t
C:iscn&
in
;I
pl;111c potcntinl
flow.
:i) AcccIcr;~ting c;~sc;ld~
(~urbo runncr)
in
notations
of absulu~c flow, with bou;ld
vortcx clcmcnts
tls
on
aria.
loguous points
(';
de1lcction
triangle,
Ac,,
C,
,
C2;
CLO
zero
lift
direction.
b) Gcomctry of
profile in c;lscadc,
C
dummy
vari;tblc of thc bound vortex
elcnlcnt
l1
ds;
2
coordinate
of the point, whcrc the kine-
matic boundary condition
is
satisfied.
c) Straight
accel-
erating cascade (turbine
runner) in notations of rela-
tivc
flow;
cl) cascade
with
a
circulation
f
about each
profile; c,) cascade substi-
tuted
by
a
vortex row, circu-
lation
f;
streamlines, and
velocities in
1
ant1
2
result-
ing from
f
and
w,.
c,)
How
to
get
deflcction triangle
from
c,)?
A
c,,/2
=
A
w,,
.
now arrallged parallel to zach other and at a distance from eacll other equal to the pitch
t
in the peripllzral direction (Fig.
6.2.1
a).
This arrangement of aerofoils is known as a straight cascade. The desired knowledge
of
tile distribution of contour velocity under a certain load and lie~lce a certain flow enables
:
tlic calculation oi the pressure distribution along the vane surface. This is required for the
?
stress c:ilculation of the rotor vane and its neighbouring p?rts, e.g. the hub or the vane
adjusting mechanism. Furthermore this enables a control of the susceptibility of the vane
to cavitation under certain load conditions.
Imagine
a
straight cascade (Fig.
6.2.1
a) with chord
L
and pitch
t.
Its stagger angle may
be
expressed by the angle
a,
the zero lift direction makes with the circumference.
A
Cnl-tesinn
coordinate system is introduced. Its y-axis points in the circumferential direc-
tion and its x-axis in the sense of the meridional speed,
when pumping. Its origin is
on
the pointed trailing edge cf an arbitrary profile, the so called zero profile.
Since all the profiles are congruent, and the
assun~ed plane potential flow of an
in
pressible fluid is imagined to be steady, the streamline flow pattern is pitch-period
Therefore the boundary conditions need only to be satisfied on this zero profile.
The indirect problem now considered asks for the contour velocity on this profile for
given
cascade Seometry and under a certain velocity
c,
at inflow.
An
arbitrary point
P
on
the contour of zero profile is deterl~iined by the arc
's',
which
assumed to be oriented in the counter clockwise sense, along the
contour of the profil
and to start from the origin
0.
The complex coordinate of point
P
is
[(s)
=
((s)
+
iq(
=
[
+
iq.
The core
of
the singularity method: The contour of the profiles is assumed to
streamline. Along this the contour velocity
c(s),
the unknown, exists. Usually in an id
210

flow
highest speeds occur on the contour. The interior of the profiles is assumed to be
filled
with
static
fluid.
lience proceeding tlorn~al to the contour the velocity makes a step
on
the contour.
From l~ydrodynnmics
it
is known, that such a step is gener:itec! by means ofa vortex layer.
that is along thc contour. I'heicfore so-called "bound vortices" with strength
:.
(s), taken
as circulation pzr unit le~~gth, and continuously varying are assumed to be continuously
distributed along the contour. Applying Stokes' theorem along an infinitesimally small
along the contour and surrounding it reveals the essential relation
The vorlex distribution might rotate in the counter clockwise sense. Hence the
ele~nellt
ds of the contour has a circulation y
(s)
tls
=
y ds.
A
straight vortex row, consisting of
elementary vortices, a distai~cc
t
from each other, having
a
circulation
7
(is
and situated
on analogous stations to the point
[(s) on the profiles (Fig. 6.2.1 a), induces, at
a
point
with the complex coordinate z, the
co~nplex velocity
dE;
(Fig. 6.2.1 b).
dE,
=
dc,,
-
i
dc,,
=
i
[y
(s)/2 t]
ds
coth {(n/r)
[z
-
[
(s)]
]
,
(6.3
-
3)
where dc,, and dc, are the components of the induced velocity in the x and g-directions,
respectively.
Splittl~lg
df7
into real and imaginary part yields [6.5]
dc,,
=
(y/2
of,
ds
,
(6.2
-
5)
f,
=
sin [2
7r
(Y
-
rl)/tl/D
,
(6.2
-
6)
j;
=
sinh[2n(x
-
<)/t]/D,
(6.2
--
7)
D
=
cos [2 n(y
-
q)/t]
-
cosh [2 n(x
-
<)It].
(6.2
-
8)
Integrating around the contour of the zero profile gives
c,,
=
(112 1)
+
Y
(s)f,
[x, Y,
t
(4,
v
(4
d-5
9
c,,
=
(112
t)
$7
(s)f, 1x9 Y,
r
(s),
17
(41 ds.
The components of the undisturbed throughflow velocity are
Cco
x
=
C",
,
C,,
,
=
Cm
cot
CI,,
where
u,
is the angle between c, and the y-axis (Fig. 6.2.1), c, the meridional speed
component. In a potential flow the velocities can be superimposed. This gives
the result-
ing
velocity
cx
=
C,
+
cy,,
c,,
=
cm
CO~
arro
+
c,,.
(6.2
-
1
3)
The boundary condition of a flow along the contour of the profile at an arbitrary point
-4
(2)
on it requires
C,
(z)/c,
(2)
=
cot
cr
(z)
,
(6.2-
14)
where
cc
(z) is the known angle between'the contour element and the y-axis. Inserting the
Velocity components from (6.2-
13)
gives

2
t
c,,,[cot u(z)
-
cot
a,]
=
jy
(s) {f,[z, ((s)]
-
cot a(z)f,[, I;(.<)]}
ds.
(6.2-
15)
'rom (5.2-35) Stokes' theorern yields the
blad:
circulatiotl
r
=
4
Y(S) ds
=
t(cY2
-
c,,)
=
t
c,,(cot
a,
-
cot a,),
(6.2
-
16)
where
u,
and
a,
are the angles between the resulting velocities and the y-axis (circurn-
ference) on thc poinls 2 and 1, strictly speaking at the infinities downstream and upsirearn
of the cascade. In 1 and 2 the function
f,
(6.2-6) tends to zero and the function
fy
(6.2-7)
tends to
f,,
=
+
1,
f
=
-
1.
This put in (6.2-C)), (6.2-
10)
with respect to
f
=
4
(s)
dS
"t
gives c,,;
=
0,
c,,;
=
+
r/(2
t).
Hence the cascade acts at the infinities as a vortex layer with
n
linear vortex density
rIt.
Better: Seen from infinity the cascade with its profiles of circulation
T,
distant
t
to each
other, shrinks to a vortex layer of vortex density
fit.
Superimposing c, and c, at the
points
1
and
2
changes only the peripheral component, namely c,,
=
c,,
-
f/(2t),
c,,
=
c,,
+
r/(2
t).
Subtracting both yields the circulation and hence reconfirms (6.2-16)
(Fig. 6.2.1 c)
.
Adding c,, and c,, gives c,,. With respect to c,,,
=
c,,,
=
c, this Proves the rule
of
c,
=
(c,
+
c,)/2. Introducing the zngles
a2
and
a,
between c, and c, and the y-axis gives
(Fig. 6.2.1 c)
cot
3,
=
(cot
a,
+
cot or,)/2
Eliminating cot
r,
from this and (6.2-16) reduces cot
r,,
usually not known, to
f
=
$
y
(s) ds and the angle
u,
of the afflux, usually given, by
cot
IX,
=
[1/(2
t
c,,)]
5)
y
(s) ds
+
cot
a,.
(6.2
-
18)
This in (6.2-
15)
yields the following linear integral equation for the distribution of vortex
strength
;.(s)
or respecting
(6.2-
1)
also of contour velocity c(s) due to a cascade of known
geometry
,r(z):
t/L,
under a given inflow angle
a,
and given meridional velocity c,
This integral equation is of the
Fredholm
type. Numerous procedures were introduced for
its solution. In this connection the publications of Martensen
[6.2], Jacob [6.3], lsuy [6.4],
Eti~rpel
[6.5]
and
Birnbalun
[6.hj
may
be
mentioned.
6.2.1.2.
Practical
solution
of
the
indirect
problem
1
For a practical solution the integral in (6.2-19) is converted int~ a sum. To this end the
periphery of the profile has to be divided into a finite number of arc elements. For
convenience the
n
+
1
elements might have the same length
h.
Thus the arc coordinate
s
for the mid points of these arc elements are s,
=
h,
s,
=
2
h
. . .
s,
=
v
h
.
.
.
s,
=
n
h.
At
each of these points the contopr velocity c(s,) is unknown.
i
Therefore the integral in (6.2- 19) is converted into a sum with c (s,) as the unknown. The
complex coordinate of
the dummy variable c(s) is now denoted by
z,.
The complex
coordinate of the
poirrt
Piz),
on which the boundary condition (6.2-14)
is
satisfied,
is-
denoted by
zi.
Thus the equivalent of the integral equation (6.2- 19) takes the form
{
n
v=
1
(6.2
-
2

in which analoguous to (6.2-6) through (6.2-7),
fx
,
zv)
=
sin
[3
71
(~i
--
yv)/t]
!n
,
f,
(zi,
2,)
=
sinh
[2
n
(xi
-
x,)!t]/D
,
D
=
cos [2
n
(jvi
-
yv)jt]
-.
~osh
[3
rt
(xi
-
x,)/t].
The systeln of (6.2-20) is written down for
n
points zi. Hence
11
inhornogeneous linear
equations are obtained for
the
unknown contour velocities
~(s,).
enablins their solution.
It
must be mentioned, that the kinematic boundary condition (6.2-
14)
loses its sensc or:
the pointed rearward edge of the profile. Therefore in good agreement with experience
!I:e
Ktltta
condition [5.15; 5.161 is introduced as
6.2.1.3.
Simplified
method after Ackermann and Birnbaurn
In this method [6.6; 6.71 the profile is simplified by. its skeleton. The bound vortices are
located along a straight line, which coincides
with the undisturbed throughflow velocity
w,
being now the x-axis (Fig. 6.2.2
a).
As the rnethod is limited to small
angles
of attack
betwecn chord and
w,,
the bound vortices, now aside the skeleton, are on
n
stretc!~ of
about chord length
L.
The continuously distributed vortices with
a
strength
it(s)
induce
at
a point
x'
a
velocity
c,,
with
L/
2
c,.,,
=
(112
TC)
y
(x) ~x/(x'
-
x)
,
cEYx
=
+
y
(xf),/2.
(6.2
-
24)
-
L/2
Analogous to (6.2-4), (6.2-5) for the components of induced speed of a row of elementary
vortices of the circulation
y
(x)dx,
now locatcd on analogous points of
a
lattice
dc;
=
[y
(x)/2 t]
f,*
dx;
dc,*,
=
[y
(x)/2
[IS,*
dx
.
(6.2
-
25)
Obviously, in consequence of a transformation from the
x,
11-system, origii~all~~ used, to
the x*, y*-system, adoptcd now
(Fig.
6.2.2
b),
the following relations exist bctwcen the
functions fx,f, fro111 (6.2-9), (6.2-
10)
and the now valid general functions f:,f,l":
Further the coordinate differences x
-
t,
y
-
q
inf;,
f,,
obviously are now transf~rmed
(Fig. 6.2.2 b) according to
x
-
<
=
(x*'
-
x*)
sin
p,,
-
Yl
=
(x*'
-
x*)
cos
e,.
(6.2- 27)
Fig.
6.2.2.
Profiles substi-
luted
by
skeletons, bound
vortices on
a
line parallel
lo
wm.
a)
Single skeleton.
b)
The
coordinate transfor-
mation from
the
x,
y-
to the
x*.
Y*-system.

Iience
for conienicncc thc star
*
is omitted. FUI-thcr from
now
on the
dummy
vari;lble
is dcrio!cd
by
x'
and
tl~c coordin;ite of the point considered
by
s.
Tlic rcl:ltions (6.2-25)
yield
LI
2
c7.x
=
5
d~y.xr
cyy
=
Lf
dc,,
.
(6.2
-
28)
-LIZ
-
1.12
Station
.u
=
s'
mrikes it advisable to split
c,
into the followi~ig two terms
1)
c,, represent,
ing the
"self induction" of the individual
skeleton,
see (6.2-24), 2)
c,,
representing
the
velocity, induced by the residual cascade
-
-
'71
-
C~~~
+
C~yx,
-
C~yy
+
C~~y-
(6.2
-
29)
Once c,,,,
c,;,
and
c,,,
c,, are given with (6.2-24) and (6.2-28), (star hence omitted!)
'RYX,
C~,y
result from (6.2-29). For a strict solution of cEY: (6.2-24). Ackernlartn and
Birnbaunl [6.6] proposed the following distribution of the strength
y
(x)
of bound vortices
(Fig. 6.2.3)
'/(.u)
=
~,~,[AYA(x)
+
BYD(X)
+
CYC(X)~,
2
112
i
)JA
(s)
=
[(I
-
2x/L)/(l
+
2 x/L)]"~, y,(x)
=
[l
-42
x/L)
]
,
f
yc(.x)
=
(2
x/L)
[l
-
(2 x/L)~]
'I2
-
YA
(416
(6.2-30)
i
3
In the above
A,
B,
C
are coefficients, which have to be adapted to the bounclary condi-
*
tions. A11 these elementary vortex distributions satisfy the Kutta condition (6.2-23),
namely with respect to (6.2-24): cEyx(x
=
L/2)
=
?(x
=
L/2)/2
=
0.
Inserting (6.2-30)
in
(6.2-24) gives the self-induced veloc~ties in the y-direction on the x-axis at the point
x
(Fig. 6.2.3)
c~,~~
=
\v,
,
CEyYB
=
W,
2 x/L,
CEyyC
=
wuo
[(2 x/L)~
-
1/31
(6.2-31)
The kinematic boundary condition
of
a sicgle profile is now satisfied approximately
on
the x-axis. This is admissible for small angles of attack and
011
profiles with small camber.
Hence (Fig. 6.2.3)
Ryldx
=
cEYy/~v,.
Assuming the skeleton to intersect the origin of the coordinate system, the following
skeletons result from (6.2-
31), (6.2- 32)
y,
=
x,
y,
=
x2/L,
yc
=
(413) x3/L2
-
x/3.
This corres?onds to the elementary skeletons and operating conditions:
A)
Flat pla
with angle of attack.
B)
Circular arc (approxi~nated by a parabola) with zero angle
c)
61
'mh,
1
LTITfi
Fig.
6.2.3.
Results of simplified singula
method.
a)
Form of skeleton due to
strength
y
of bound vortex and
2)
Fvic~
L&JJ
b) Velocity induced by
y
on
a
sin
'.f
B
skeleton normal
to
it.
c) Distri
y,
with Kutta condition always sati
"-77-
m
1
plate;
2
single cambered skel
CY
EC
3
double cambered skeleton.
214

attack
against its chord.
C)
Double carnbered skcleton with zero angle of attack against
cll~~d,
(Fig.
6.2.3).
-
~etcrlninstion of thc
coefficients
A,
B,
C
after
Pnt~tcll
(4.101:
,)
Single aerofoil
(E):
Dividc the small assumed inclination and angle
djlcls
of the
&eleton at an arbitrary point
x
=
xi, into
1)
(5
as tlie angle of attack, the chord makes
with
M',,
2) as the angle, the chord makes with the skeleton (Fig. 6.2.4), according to
1r!serting this and
c,,,
=
ACE,,,
+
BcE,,,
+
Cc,,,,
from (6.2-31) into (6.2-32), gives
with A
=
A,,
B
=
BE, C
=
C,,
Fig.
6.2.4.
Gcornetry of skeleton
s
and its
chord
L,
angles
Si
and
6.
Writing down this relation for the three stations
I,
=
-
~fi/4,
x,
=
0,
r,
=
~$14
(so-called
Rir~lbaum
stations), where the angle
8,
has the values
3,,
3,, 3,,
this linear
system gives
A,
=
d
+
I(,;
BE
=
K2;
CE
=
K3,
(6.2
-
36)
After
Kutta
and
Jotlkovsky,
according to (5.2-29), the aerodynamic
lift
on an aerofoil,
chord L, span
1,
under the undisturbed velocity
w,,
depends on the circulation about
the aerofoil
r
by:
FA
=
Q
lv,
T.
Expressing
FA
through the
lift
coefficient
CA
as
FA
=
([,/2)
Q
W:
L
and eliminating
FA
gives the general relation between circulation and
lift
coefficient
With the circulation resulting from
y
(x)
(6.2-36)
the lift coefficient in gcneral is obtained from
For the single skeleton
(E)
with its coeficients from (6.2-36) and (6.2-37), the last
relation is converted into

The
:ingle betwcc.n
zero
lift
direction
(<,
=
0)
i~nd
chord, the
SO-called
zero
angle
of attack
follows rrorn this as
Obviously (Fig. 6.2.4)
tlie so-called physical angle of attack
So,
between zero lift direction
(due to the aerofoil's geometry),
and
the undisturbed velocity
kv,
results fro111
Inserting this into (6.2 --41) gives
The
exact theory would yield 2
n
sin
do,
which makes nearly no difference for the small
angles of attack 6,
(
<
15")
considered 11c1-e. In rcality the constant is smaller than 2
namely
4,8 for slim profiles and up to 5,5 for thicker ones. The reason, discussed in
[5.2]
is given by the fact, that the real profile is accompanied
by
boundary layers and wakes,
the displacement thickness of which has to be added to the solid aerofoil.
b) The aerofoil in cascade
(G):
Here an aerofoil with the geometry of the above single one
%
is
arrangcd in a cascade. The following three problems arise from this:
a
1)
How does the
lift
coeflicient (important for dimensioning
a
rotor vane) depend now
?
on the physical angle of attack
So?
2) What is the ratio between lift coefficient of aerofoils in cascade to that of the single
aerofoil,
ivhen the physical angle of attack is retained (so-called cascade factor)?
3)
Ilov; docs the zero angle of attack depend on the geometry of the aerofoil and the
cascade?
Assuming relatively small induced velocities
c,,
of the residual cascade as compared with
those
c,?
due to self induction and as compared with
irv,,
compatible with the basic
1
assumpt~o~i of small angles of attack, the kinematic boundary condition corresponding
I
to (6.2-32) map be approximated with the y-component of induced velocity
c,.
Accord'
l
ing to
(6.2
-
29)
this is composed of c,,, and c,,,.
1
With
c,,,.~
=
bv,
(AG
cRl
li.+
BG.cRY
Bi
+
CC
cIY
,-,),
i
denoting the point considered, th
kinematic boundary
cond~tion is now dylds
-
(c,,
+
c,,,)/~v, and beco~rles with
cE
from (6.2-31) and dy1d.x from (6.2-34) for the point
x
=
xi
6
+
9,
=
A,
(1
i-
c,,
,,)
+
B,
(2 xi/L
+
c,,
,i)
+
CG
[(2
x~/L)~
-
113
+
c~~ ci]
-
If
the profile with its angles
3,
in the cascade
is
the same as the single one and if also t
angle
of
attack
6,
the undisturbed speed
w,
makes with the chord, is the
same
in bot
the cases, then the left hand sides of both the relations (6.2-35) and (6.2-45) are the
Sam
and hence can be eliminated.
Applying
tlie remaining system at the three points
x,
=
-
L
d/4,
x,
=
0,
x,
=
L
three linear equa!ions arc obtained for the coefftcients
A,,
BG,
C,
(due
to the aero
cascade) as a function of the coefficients
A,,
13,,
C,
(due to the single aerofoil) accordi
to (6.2-36), (6.2-37). Hence
A,
=
f
(A,,
BE,
CE)
etc.
Introducing now
the coefficients
A,,
B,,
C,
into (6.2-40) gives the lift coeflicient
cascade
of
a certain aerofoil with the angles
yi
and hence certain figures
Ki
from
(6.2-
as
iAC
=
(C11C4)J
+
(C1
K1
+
CZ
KZ
+
C3 K3)lC4,
21
6
