Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment

tions, in which thc

Y

value in thc middle of a certain area element is

expressed

as a linear function

of

the

Y

values at points along the boundary of this arca.

.

Schilling

[6.17]

also presentcd some examples for the solution of this mcthod. It must be kept in mind

that thc nlcthod gives infornlation only about the flow within thc mcan stream surf:icc of thc

flow

.

lamina considcrcd. The subdivision of the flow in a rotor of givcn geometry into flow laminae or

elementary

turbines is considcrcd in Cap.

6.5.

The deviation of real flow from an axially symmetric one is considered in Cnp.

10.6.

The objection,

that the

method is wrong as it does not account for the vorticity in the absolute flow is weakened

by

the fact that the absolute vorticity in the free flow outside the boundary Iaycr and the

wakes

from

a cascade upstream in general is small and has a prevailing component in thc streamwisc direction.

This only twists somewhat the streamface within the rotor channel, Cap.

10.6.

Problems due to unsteady flow, vortices passing

a

cascade, boundary layer, wakes, and

flow

about

the inlet edge arc dealt with in the

chaptcrs

6.4;

7.2;

7.3

respectively.

Naturally

the method presumcs an attached flow. Any stall, e.g. past the inlet edge, 3s reported by

Betz

[5.11],

which may be attributed to a wrong estimate of thc inflow controlled by the guide vane

is predictable by continuity,

niomentum and energy theorem.

.

5.2.5.

The

rate'of

strain

tensor

Consider

a

certain flow with velocity components c,,

c,

and

c,

at a certain point

P.

These

velocities vary at a distance

dn

=

dx

+

dy

+

dz

from the first point by the following

amount here given for the component

c,

only

Due to the local curl and the

rcsulting angular velocities

a,,

ox

of the flow, the fluid gets

an additional induced

velocity in the x-direction, for example at the neighbourizlg point

P,

(Fig.

5.2.2b)

dc,,

=

w,dz

-

o,dy.

Substraction of

dc,,

from

dc,

yields the velocity increment in the x-direction due to "de-

formation"

Obviously:

dxldn

=

cos

(x,

n);

dyldn

=

cos

(y,

n); dzldrz

=

cos

(z,

n).

Dividing

dc,

,,,

by

dn

and respecting the last relations yield the x-component of "strain rate"

as

a function

of

the direction the strain rate exists, at which the direction is given by its unit vector

nO(cos(x,

n),

cos(y, n), cos(z,

n)):

This relation shows that the derivative of thc "deformation velocity

"

in a certain direction

depends linearly on the components of the directional vector

no.

Therefore the derivative

of

the deformation velocity is a tensor of the unit vector

no

according to

dcdef/dn

=

Kno,

with

T,

as the following rate of strain tensor

7.1:~ coniponcrlts of

7;

are large

in

rcgions where the curl is also Inr-go, e.g. in b01111dar~

I:tycrs. On

thc

oilier Iiand,

it

solid body vortcs has

n

curl but no

x,

whcrens the free vortex

has.

5.2.6.

The

circulation

and

its

relation

to

curl

The circulation

f

about the contour of a rotor vane in a turbo machine is an important

feature,

iieeded to obtain the forces acting on

it.

In

general

r

is dofined by

a

line integral

along a line

I,

which usually is closed, by

In a plane and steady potential flow about an aerofoil but also

about

a

cylindrical vane

section of an axial turbo machine,

r

originates from a physical angle of attack

So,

the

undisturbed

flow

makes with !he zero

lift

direction due to the profile.

More generally the curl from

(5.2-8), (5.2- 10) is defined by

(A0

being unit vector)

curl

c

=

lim (§cds/tl~)

AO.

dA

-0

(5.2

-

30)

I-Ience

Stokes'

theoreni, which relates the circulation along an arbitrary spatial closed line

to the flux of vorticity curl

c

through a surface, that ends on this line [4.26]:

In mixed flow turbo machines the circulatiorl about a rotor vane, and the velocity dif-

ference

IV,

-

\tp,

bet~veen the suction and pressure faces of rotor vane hence dzrived,

depends ~n;~inly on the relative eddy curl

w.

The link between curl

tv

and

bv,

-

rv,

in such

a

niachine can be found as follows by (5.2-31).

Consider

an

ele~nentary quasi-parallelogram (Fig. 5.2.3

a)

on the axisymrnetric streamface

of

a

rotor vane channel. limited by a streamline element

ds

along the suctioli and pressure

"

faces of the rotor vane and the unobstructed pitch arcs along two adjacent parallel circles

-

t~ith tlie radii

r

and

I.

+

tlr- respectively.

For an

irso

tational absolute flow curl

c

=

0, Cap. 5.2.4, the relevant component of rela-

tive eddy

riorrnal to the strezmface, making an angle

p

with a plane normal to the rotor

axis,

beconles

(LU~I

H'),

=

-

20

cos

p.

The unobstructed pitch between the

z

rotor vanes

due to a contraction

factor

@

in consequence of the boundary layer and vane thickness

is

Lnr

@/z.

The relative flow is along the vane and has, according to the local velocity triangle,

a

pitch-averaged relative whirl colnponent

~v,

(Fig. 5.2.3a). With respect to the obvious

relation

Jr

=

tis

cos

11

sin

p,

P

being the angle the vane makes with the circumference,

St0kr.s'

theorem

(5.2-31),

now applied to the quasi-parallelogran~, gives the di

relative velocities between suction

(S)

and pressure

(P)

face, at

cf,

=

const, as

\r.,

-

lr.,

=

2

n

@

cos

,u

sin P(20r

-

d(lv, r)/dr)/z.

Here for pump turbines and pumps with backward curved rotor vanes, the following

relation holds good:

\rl,

=

tor,

=

const. Hence d(lv,r)ltlr

z

wrl. For high head

ranc cis

turbines ivith pronounced foreward curved rotor vanes, wur is approxin~ately constan

Hence d(lr,r)/llr

=

0.

178

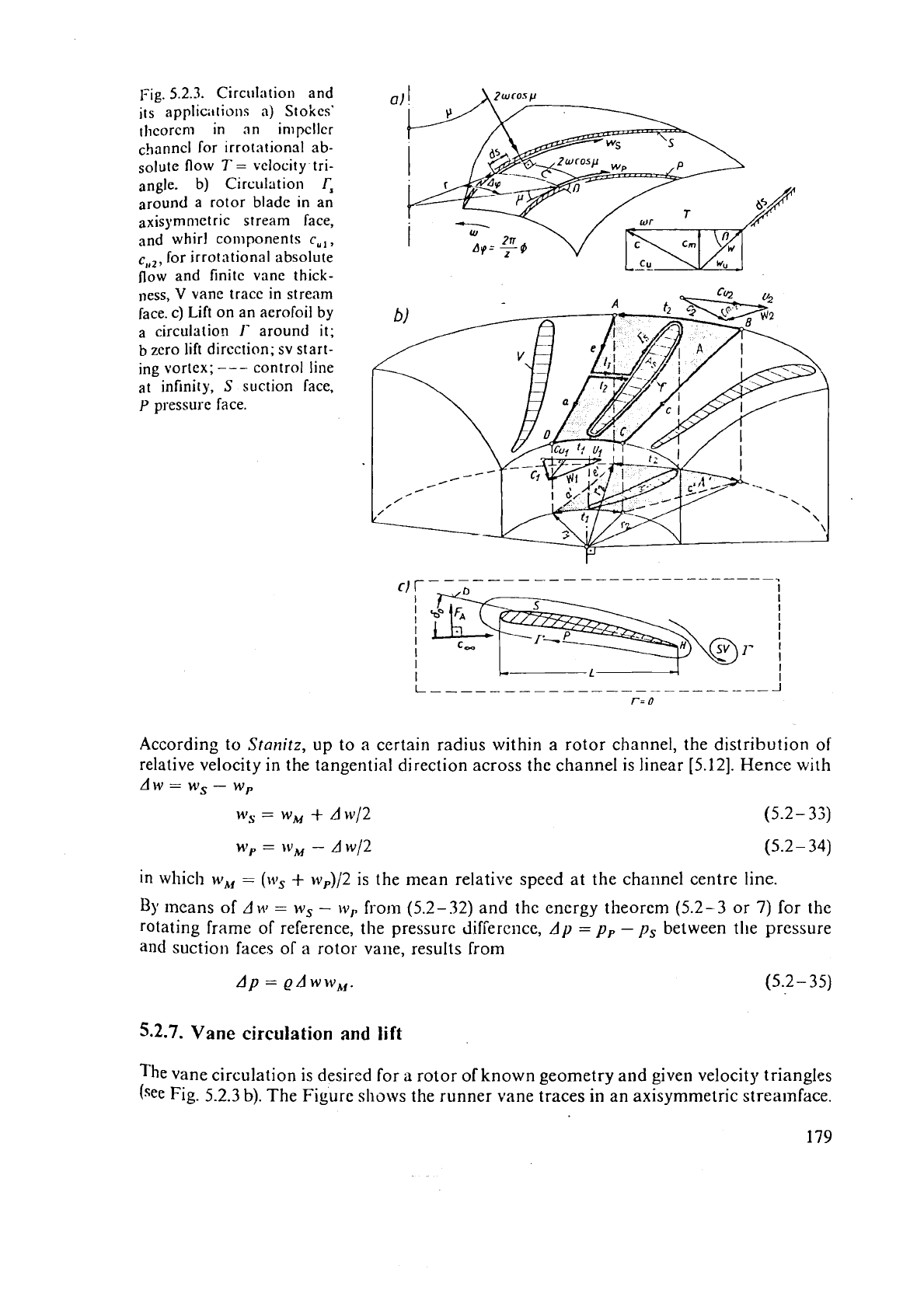
1-ig.

5.2.3.

Circolation and

its applic;ttions

a)

Stokes'

thcorcni in

nn

inipcllcr

for irrotationsl ab-

solute flow

T

=

velocity tri-

angle.

b)

Circulation

f,

around

a

rotor blade in an

axispmnletric stream face,

and whirl components

c,,

,

c,,,,

for irrotntional absolute

flow and finite vane thick-

,less,

V

vane trace in stream

face. c) Lift on an

aerofoil

by

a circulation

I'

around it;

b

zero lift direction; sv start-

ing vortex;

---

control line

at infinity,

S

suction face,

P

pressure face.

According to

Stanitz,

up to

a

certain radius within

a

rotor channel, the distribution

of

relative velocity in the tangential direction across the channel is linear [5.12]. Hence with

Aw=

w,-

W,

w,

=

w,

+

A

rv/2

(5.2- 33)

in

which

w,

=

(w,

+

wp)/2

is the mean relative speed at the channel centre line.

By

means of

AMJ

=

w,

-

w,

from (5.2-32) and thc energy theorem (5.2-3 or

7)

for the

rotating frame of reference, the pressure difrercnce,

Ay

=

p,

-

p,

between tlie pressure

and suction faces of

a

rotor vane, results from

5.2.7.

Vane

circulation

and

lift

The vane circulation is desired for

a

rotor

of

known geometry and given velocity triangles

(see

Fig. 5.2.3

b).

The

Figure sllows the runner vane traces in an axisymmetric streamface.

Tht:

;ibsolutc

flow

ir

irrc)tation;~l. From

(5.2-31).

thz circuliitinn

I-

aroiind the nrc:i

A

w~th~n

the

>rrcnlnf~cc,

~11;lt

sr~rroi~nds thc

vane

trace

A,

2nd

cstct~cls pcriplicr;llly over one

pi:cli (Fig.

5.2.3

b).

obcys the

relation

$

(1s

+

$,

br

ds

+

$

,vds

+

,u

11s

+

4

I\$

cls

-t

$

Ir

11s

t

$

)V~S

-k

8

1~

(1s

11

e

11

1

Iz

n

f

I

c

=

jJ

curl

)vclA.

A

AS the axially oriented relr~tive whirl is the only existing vortex, then

jj

curl

~vti~i

=

A

curl

bv

tlA',

v~.ith

A'

as the projection

of

A on

a

plane nornlal to the axis. With the

-4

'

relative eddy

-

2w,

and respecting the vanishing vortex through the vane's projection

A:

oil

a

plane nurmal to the axis, then

1.5

curl

wdA'

=

2n(11(r,2

-

r:)/z

-

20A:, (5.2

-

35)

.I

'

with

z

as the number of blades. Obviously from the velocity triangles

$wds

=

tvUi2nr/z

li

=

2;r

(wrf

-

c,,r)/z

(i

being

1

or 2 at the rotor inlet or outlet) the circulation about

A

reads

2 2

f

=

-+

(2n/z) [0)(r2

-

rl)

-

cu2r2

+

c,,,

r,].

(5.2

-

36)

Equating

P

and

51,.

curl

w

dA' according to

Stokes'

theorem, the circulation nbou

t

the

rotor

vane leads

=

(275/z)(cU2r2

-

cU1rl)

-

20A:.

(5.2

-

37)

The

last term

2~:),4:

appears only in mixed flow machines

and

increases

with vane

th~ckness compared with the radii

r,

or r,, respectively. It results from the absence of

flux

of

rri;~ti\e

eddy within the contcjur of the rotor vane.

In

axial

rurborn~chines with coaxial cylicdrical stream surfaces thc area

A:

is zero. Hence

Ctlr

=

(2nr/z)(c,,

-

c,,)

=

dc,t,

(5.2

-

38)

in which

t

is

thc

pitch, and Ac,,

=

c,,

-

c,, is the so-ca!led deflection [5.13].

Thc

now in such

a

cylindrical surface shall be a steady potential flow, of unit depth. Let

c,

-

cor:st

be the undisturbed velocity. As is well-known

[5.14],

the lift on a vane with

circuiation

/;

equal5 ihat on

a

bound vortex tube at its centre of pressure, strength

curlc

=

Q,

cross section rlsdn, Js being along c,,

drt

normal to it. Henceforth:

g

=

0.

'The

equation of notion (5.3-2) yields

a

pressure on this vortex in the n-direction

:

dp

=

p

lc,

>:

SZI

tiit.

Hence according to

Krttra, Jotlkorsky

[5.15; 5.161, with the circu-

lztion

P,

about thc vane, bcing according to

Stoltes'

theorem

T;

=

R

Jsdc,

and the unit

?

1-ector on

the

flow plane

52'

=

Q/Q,

the hydrodynamic lift on the vane becomes

(see

'

Fis.

5.2.3~)

F,

=

g(c,

x

52')

<.

(5.2

-39)

5.3.

Dynamics

of

ideal

flaw

5.3.1.

Eqxation

of

motion

and

cnergy

foi

a

st:rtionary frame of reference

For

the

absolute flow, observed from

a

stationary frame

of

reference, the equation

0

motion

of

a

unit mass reads

1

SO

grad@/@

+

c2/2

+

gh)

=

c

x

curlc

-

acldt,

(5.3

-

1)

in which

p

is thc pressure,

Q

the density,

c

thc absolr~te vclocity,

II

the elevation of the point

considered. An clement of an

ii~stantaneous streamline is parallel to the vslocity vectc-r

c.

An element of the instantaneous vortex line is parallel to the vector curl

c.

At any

instant the vector c

x

curl

c

is

normal to the surrdce element, formed by the instantaneous

vortex and stream line

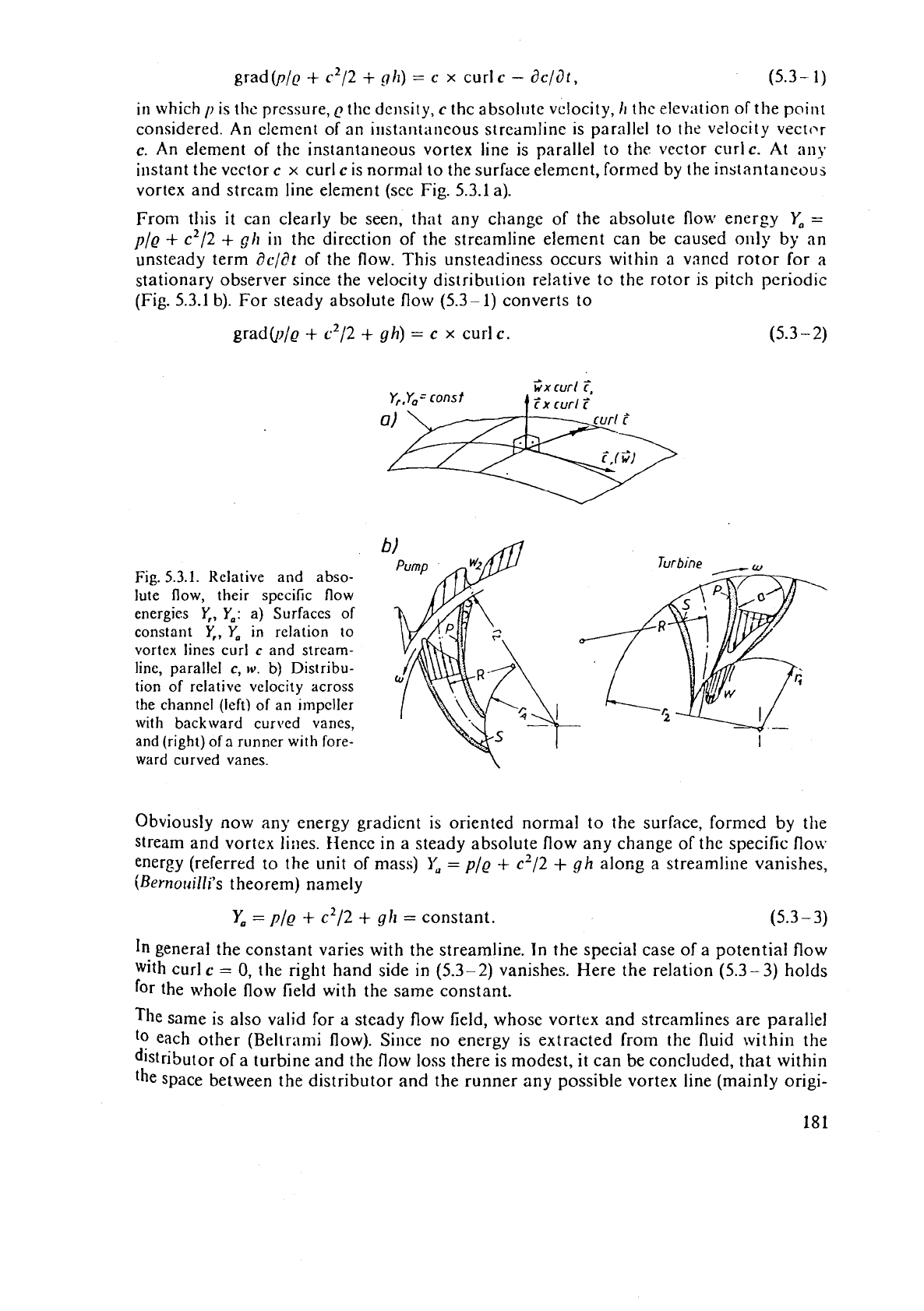
element (see Fig. 5.3.1 a).

From this it can clearly be seen,

that any change of the absolute flour energy

Y,

=

P/Q

+

c2/2

+

~II

in the direction of the streamline element can be caused only by an

unsteady term

dcldt of the flow. This unsteadiness occurs within a vaned rotor for a

stationary observer since the velocity distribution relative tc the rotor is pitch periodic

(Fig.

5.3.1

b).

For steady absolute flow (5.3-1) converts to

grad@/@

+

c2/2

+

gh)

=

c

x

curl c.

(5.3

-

2)

Fig.

5.3.1.

Relative and abso-

lute flow, their specific flow

energies

Y,,

Yo:

a)

Surfaces of

constant

Y,,

Y,

in relation to

vortex lines curl

c

and stream-

line, parallel

c,

lv.

b)

Distribu-

tion of relative velocity across

the channel (left) of an

ilnpcller

with backward cursed vanes,

and

(right)

of

a

runner with fore-

ward curved vanes.

Obviously now any energy gradient is oriented normal to the surface, formed by the

stream and vortex

1i:les. Hence in a steady absolute flow any change of the specific flow

energy (referred to the unit of mass)

1;

=

p/~

+

c2/2

+

gh

along a streamline vanishes,

iBernouilli's theorem) namely

Y,

=

p/~

+

c2/2

+

gh

=

constant.

(5.3

-

3)

In general the constant varies with the streamline. In the special case of

a

potential flow

with

curl

c

=

0,

the right hand side in (5.3-2) vanishes. Here the relation (5.3-3) holds

for the whole flow field with the same constant.

The same is also valid for

a

steady flow lield, whose vortex and streamlines are parallel

to each other (Beltrami flow). Since no energy is extracted from the fluid within the

distributor

of

a turbine and the flow loss there is modest, it can be concluded, that within

the space between the distributor and the runner any possible vortex line (mainly origi-

nating

froin

a

change

of

circulaiion

over

the span

fa

distriblltor vane) must

bt.

parallel

to

the

strcarnlincs

[5.10].

5.3.2.

Equation

of

motion

and

energy

for

a

rotating

frame

of

refcrerlcc

Relation (5.1

-

I)

can

be

adapted to

a

rotating frame of reference, when the absolute vel-

ocity

c

is replaced

by

the relative velocity

tv

and the centrifugal force on unit mass due

to rotation

-

Erad(r.20)2/2)

and the Coriolis forcc on unit muss

-

2)v

x

w

arc

added to

the left hacd side of

(5.3

-

1).

Hence

grad(y/p

+

,v2/2

-

r2u2/2

+

gl~)

-

2

w

x

o

=

IV

x

curl

w

-

d)ujdt.

(5.3-4)

VJith the trarlsformations curl

u

=

curl

w

x

r

-

20;

u

+

iv

=

c;

and curl(u

+

w)

=

curl

c,

the equation of motion now reads

grad(p/,o

+

\v2/2

-

r2m2/2

+

gh)

=

)v

x

curl

c

-

aivlat.

(5.3

-

5)

Now instead of the absolute flow energy (5.3-3), a rothalpy appears without the term of

internal energy, according to

Y,

EE

P/Q

+

\v2/2

-

r2w2/2

+

gh.

(5.3

-6)

On this occasion the individual terms of thc encrgy

Y,

and

Y,,

all having the

dimensions

of encrgies

per unit mass, will be comparatively interpreted.

p/p

is a positive displaccmcnt work done by the unit

mass of fluid, when shifted to a

rcgion undcr zero prcssure.

c2/2

ant1

\v2/2

are thc kinetic energies

due

to

the uriit mass of fluid and

gh

the potential energy

of

it in the

terrestrial

gravity field. The term

-

r.'o2/2

can be understood as the nesative work donc

by

thc prcssure, that balances the rotary

systcm, to rnove a unit mass of fluid from the axis to a point on the radius

r.

It

may be nlentionec! that any real machine has to utilize the specific energy of a fluid within given

surroundings (altitude.

prssure, temperature and hence critical pressure) at inlet and outlet. More-

over

a

fluid ilo~ving through a machine performs positive and ncgntive

displacement

work on the

system, when entering or leaving it.

Furthx

a

recl slightly com~ressible liquid also performs expansion work within the machine. To this

strictly speaking the

chanze of internal energy of thc fluid, neglected herc has to be accounted for.

At last for esr?nomical reasons !he flow has to pass through finite cross scctions, necding considerable

s~eeds to

?:~ss.

a source of losses or strictly speaking of converting orderly motion into heat.

The specific flow enerzy

K,

al~d the rothalpy (an expression used here against convention

also

witho~t the internal energy term) are linked to each other by tlie triangular relation

Cz

=

,,.2

-

r'02

+

2cu1.(o.

This gives in the case of steady Gow and absolute irrotational

flow (curl

c

=

0)

Y,

=

Y,

+

curto.

(5.3-7)

On

many occasions the same equations and statements may be used

for

either a turbine

or an

impeller pump. However the components in turbines and impeller pumps (from

no\v on referred to as pumps) have different names.

When

this occurs, the name for the

component in a turbine is followed by that for a pump in parenthesis or vice versa.

For the steady relative flow, which may be possible in

a

machine with suffiziznt distance

between the

rclnner (impeller) and distributor (diffuser) from (5.3-5):

grad(p/p

+

w2/2

-

r2w2/2

+

gh)

=

w

x

curlc. (5.3

-

8)

Hence the grad

2;

is normal to the relative streamline and vanishes along it. Thw

Y,

=

constant along the relative streamline in steady relative flow

(Fig.

10.3.20).

This

constant is the same for any relative streamline

if

the absolute flow is irrotational

c

=

0).

For the real flow with dissipation

a,,

along the relative stream tube of the rotor between

the stations

2

and

1

due to the rotor's section of high and low pressure, the integrated

(5.3-S) is converted into

(A

now difference)

where

e

is the internal energy per unit mass of the fluid. According to energy theorem,

alld assuming the heat flow into the rotor to equal

@,,,

the difference of internal energy

1

follows as

e2

-

e,

=

O,,

+

Jpdu.

-

2

Thc tern1

d:plC)

corresponds to thc surplus of displacement work,

A:

gh

of gravity work,

A:

r2

oJ2;2

to that of centrifugal force due

to

rotation,

A:

w2/2

to

that

of

kinetic energy, all referred to unit

mass.

The

surplus

is

understood

as

the value

at

station

2

relative to

1.

The

measurements of

Bur

[5.17]

and

Srhlemmer

[5.18]

have reconfirmed relation

(5.3.-9).

5.3.3.

The role of

unsteadiness

for

energy

transmission

From the velocity triengle (Fig. 5.2.1) assuming the blade speed is constant:

rlcidt

=

dat/dt.

Furthermore the followii~g relation holds between the peripheral angle

cp,

of

a

point on the rotor, measured from a stationary radius and

cp,

rneasured from a radius

rotating with

angulal- velocity

to,

t

as the time elapsed since the instant, when both radii

coincided:

q,

=

cp,

+

tor.

Since

d{p,/dt

=

o,

dq,/dqr

=

1,

w

=

~(49,~

1)

yields

d~vldt

-

(a,vli?q,)

(8cyr/dq,)

rl

q,/dt

+

a

w/at.

Hence

From this it is seen,

that even when the relative flow is steady

(d~c,/df

=

0),

an

unsteadiness

of absolute flow is caused by the variation of relative velocity over the pitch of the rotor

channel

(dw/i?cp,

+

0),

(see Fig. 5.3.1 b).

This variation of

~c

gives from (5.3-6) for the case

Y,

=

constant (i.e. absolute potential

flow) the variation of pressure across the channel and with it the differential pressure

on

a

blade element of the runner (impeller). This enables the conversion of shaft work into

flow energy and vice versa.

5.3.4.

The

momentum theorems

I.

Gcneral remarks: The application of the energy equation

and

the equation of motion

requires a detailed knowledge of the flow field. In some cases,

e.g., that of the jet oilto the

bucket of an impulse turbine, the flow field on

a

definite face is known, e.g. on the jet cross

section upstream of the bucket. From this starting point, the force which is exerted by the

fluid on a particular body is required, e.g. the force the jet exerts on the runner.

11.

The momentum theorem: For the solution of this task, an inner control surface on

a

body (Fig. 5.3.2a) with unknown force

i.'

is surrounded by the fluid, that is enclosed by

an

outer control surface

A,

on which the pressure and the momentunl flow are known

lheoretically or by measurement.

Newton's equation of motion is applied to the fluid within this control space, see e.g.

fiucketdrodt

[5.3].

As this holds good for a certain

fluid

mass, special attention has to be

Fig.

5.3.2.

The

rnolnentum tlieorcm.

a)

Con-

trot

surfaces,

o cxternal,

i

internal,

for compu-

tation of force

I;

on

an

aerofuil.

b)

Control

SU~~CC

for

tI,e

co~nputarion of

tile

torque on

a

-

rotor

in

elevation.

c)

Shock loss.

paid to the fact that this mass now passes through the outer control surface, acting on

it by its momentum, when entering the control volume

a~:d reacting, whcn leaving it.

Hence

wit11

k

as

a force per unit volume the momentum theorem for the control vol~tme

V

and its outer control surface

A,

reads

The

first

term on the right hand side

is

due to the volume force within

V,

the second due

to pressure on the outer control

surkce

A,

tile third due

to

the flow of inomentun1

tllrozgh

A,

and the fourth due to the rate of monientuni within the volurne

V

111.

The Angular momentum theorem: This relates the unknown moment

M

on the sub-

merged body (Fig.

5.3.2 b) to the known moments exerted oil the control vo!ume

V

and

its outer control

surface

A

by

the force terms in

(5.3-

11). Hcnce the theorem

5.3.5.

Problenis

using

the

moralenturn

and

energy theorems

5.3.5.1.

Euler's

equation

For an ideal

fluid

(e

=

O),

and

a

steady absolute potential flow following frcm an infinitely

high vane number in the rotor, the proof of Euler's equation is easy. Then with

u

=

ro,

;

gH

=

Y,,

-

Y,,

from (5.3-7) and (5.3-9) it follows

For the

real

unsteedy absolute flow through a runner the angular momentum theorem

'

(5.3-12) has to be applied. First, the runner is surrounded by a control surface

A

(Fig.

5.3.2

b).

This

follows the internal, wetted surfaces of hub, shroud and vanes and

is

f

closed before tile rotor inlet

2

and behind the rotor exit

1

by axisyrnmetric faces

A,

and

3

4

A,,

with a distance lrorn the inlet and outlet cdges

of

blades such as to have whirl vel-

ocities

c,, and

c,,

uniform along the periphery.

Leakage

is neglected. Hcnce the mass flow

through the

rri~iner crosstx only through the

fdces

Az

and

A,.

The disk friction on the outer faces of hub and shroud is disregarded.

Because of the

axisymmetrically assumed flow through the faces A? and A,, the surface

forces there due

to

p

do not exert a torque about the axis, and those due to

or

are

negligibl~. The asisymmctric volume

V

excludes any torque by weight.

The torque on the runner

121,

is transmitted by wall pressure and shear stress on the

\vetted surfaces of vanes, hub and shroud mentioned above.

Assuming either an elemenlary runner of small breadth

b

and axisymmetric streamfaces

with the radii

r,,

r,

and the whirl components

c,,,

c,, at

2

and

1,

or

a

real runner of finite

breadth b, in which

r,,

r,, c,

,,

c,, are mean values over the spans")

I),

and b,, th: angular

momentum theorem (5.3-

12),

considering the ul~steady absolute flow in the runner

(Cap. 5.3.3) gives the torquc as

The disappearance of

the

unsteady term

in

the final solution of the torque nlay be realized as follo\vs.

Consider

a

volume strip

dV

of clc~nenlary breadth

cib

and elcmcntary llicridio~lal

length

ds,

along

the unobstructed

pitch

2nr@/z

(z

being the

vane

number,

cfj

the

contraction coefficient due to

the

thickness of vane, and wall-attached stall). The relevant component of

(I.

x

c)

is

rc,.

The

absolute

whirl

velocity

c,

along the pitch can be split into a timc-independent, pitch-averaged

term

c,,,

and into a pitch-periodical tcrm

el,

whose pitch-averaged valuc vanishes according to

2n9/z

0

=

(

cidip,

cp

bcing

the

peripheral angle.

0

Hence, the only unsteady contribution of

d

V

to the unsteady torquc term

dill:

in

(5.3-

13)

reads as

2

x

O/:

er2ds,db

I

(dc:/Zt)

dcp,

and this term vanishes according to

thc

definition of

c:

and

thc

obvious

0

relation

at

=

aq/w,

in

which

w

is

the

angular velocity

with

which

the

increment

of azimuth

dq

is

covered

in the timc interval

21.

Hence the torque of the runner

Note that the

whirl

cUi

here is in the sense of the runner's rotation with angular velocity

o.

Hence the so-called peripheral output

P,

=

oMa.

In a real turbine with a peripheral

cficiency

q,

(due

to

loss in the distributor, the runner the draft tube and due

to

exchange

of momentum between rotary and stationary parts), this output is also given as

P,

=

1n

g1-I

q,.

Elimi~~ating

P,

with

rto

=

u

yields

Euler's

equation, originally cited without

5.3.5.2.

The

shock

loss

due to diffusion and deflection

At

the inlet of vaned cascades, e.g. rotor, when a turbomachine operates away from the

bep,

its throughflow velocity is subjected to a sudden change in magnitude and direction.

2____

'1

Span

(here and elsewhere, sometimes also denoted

by breadth)

defines an extension or

a

rotor normal

10

its

meridional streamlines.

'I'lic

resulting

sliocL-loss, espcciully in thc casc of dccclcrntion, is stildicd on the nlodcl of

icle:~l c~~~c-Jirncnslo!i:~l, ste;lcly pipe

flow

(Fig.

5.3.2~).

The shock loss

d

Y,

appeilrs as

;I

change of specific

flow

energy

Y,,

as

in (5.3-3). between

inlct

and

oiltlet of the hatched control face (Fig. 5.3.2~) due to the sucidcn cl~aiigc

of

cllan~lcl gcomctry. Hcnce

To oliniinilte

the

pressure term, the inomenturn theorem

ill

the horizontal direction

is

appIicd on thc hatched control hcc with rcspcct to the mass illflux

ril

=

@C2Ar

By means of continuity,

c,A2

=

c,Ao,

the pressure term may be

expressed

by

(pl

-

p?)!~

=

c$

-

~,.~c,.

This in

(5.3-

17)

2

A

Y,

-

(c,

-

2clxc2

+

cf)/2

=

(c,

-

c2),/2

=

cf/2.

(5.3- 18)

In practice, a correction factor

cp,

<

1

is added to the right hand side. This is essential to

distinguish between accelerating shock

((ps

-,

0)

and decelerating shock

((p,+

I),

Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment

Подождите немного. Документ загружается.