Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment
Подождите немного. Документ загружается.

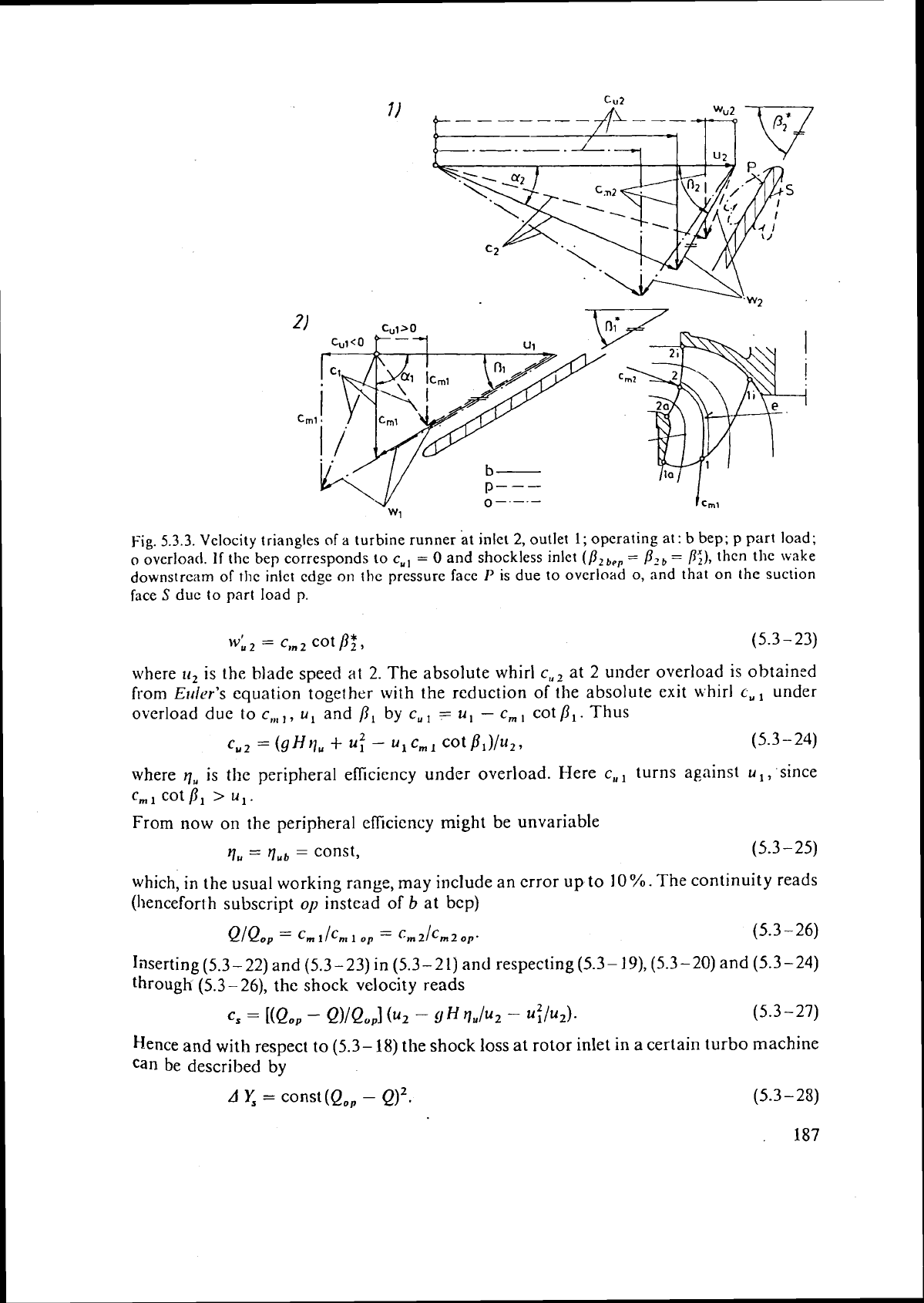
Fig.
5.3.3.
Velocity triangles of
a
turbine runner
it
inlet
2,
outlet
1;
operating at:
b
bep; p part load;
o
overloatl. If the
bep
corresponds
to
c,,
=
0
and shockless inlet
(fl,,,,
=
P2,
=
P(;),
then
the wake
downstrcam of
rhc
inlct edge
on
thc pressure face
1'
is due
to
overload
o,
and that on the suction
face
S
due to part load p.
where
u,
is the blade speed at
2.
The absolute whirl
c,~
at 2 under overload is obtained
from
Elder's equation together with the reduction of the absolute exit whirl
c,,
under
overload due to
c
,,,,
,
u,
and
/I,
by
c,,
=
u,
-
c,,
cot
13,.
Thus
c,2
=
(gfi11,
+
u:
-
UIC,,
cot81)/~2,
(5.3
-
24)
where
q,,
is the peripheral efficiency under overload. Here
c,,
turns against
u,,
since
c,,
cot/?,
>
u,.
From now on the peripheral efficiency might be unvariable
q,
=
q,,
=
const,
(5.3 -25)
which, in the usual working range, may include an error up to
10%.
The continuity reads
(henceforth subscript
011
instead of
b
at bep)
Iilserting (5.3
-
22) and (5.3
-
23) in (5.3
-
2
1)
and respecting (5.3
-
19),
(5.3
-
20) and (5.3
-
24)
through (5.3
-
26),
the shock velocity reads
c,
=
[(Qop
-
Q)/Q.,l(.,
-
~Hv,/u~
-
u:/u~)-
(5.3
-27)
Hence and with respect to (5.3-
18)
the shock loss at rotor inlet in a certain turbo machine
Can
be described by
A
Y,
=
const (Q,,
-
Q)2.
(5.3-28)

7'his holds cspcci;~ily for the ilccclcr;iting shuck.
111
.i
turbine this occurs uitdcr nvcr!oiid ;ind
in
a
piinlp undcr p;irt lo;irl. Strictly spc;iki~ig tlic Ci~scril~fi~ti
of
tlic bcIi;iviot~r
01
;1
givci~ hydro turbo-
m:ichine rcquircs tlil'fcrc:it va!iics
of
thc const;int in
(5.3
2s)
in
thc part an~l ovcrlond rangc. TIlis
is
a
conscqucnce
of
tlic tliflcrcnt tlissip;~licin by shock in accclcrt1tioli
and
ticcclcr;ltion. Thc validity
of the above shock loss rel;ltion also for
a
pump can be provcd murc c:~sily th:ln
~I~OVC
by means
of the velocity tri31igles at tlic leading cdgc of a pump rotor thcn v;~lid for thc iliffcrcnt loads shown
in Fig.
8.2.10.
5.4.
Theory
of
real
fluid
flow
5.i.l.
Properties
of
real
liquids
I.
Compressibility: Compressibility is defined
by
the relative change of density
delg
under
a
pressure increment
dp
by (5.2--4) in which the bulk rnodulus
EL
for water at
290
K:
E,
=
2.1
.
lo9
Pa. Hence
Q
varies even under the acuinl highest head (ReiOeck,
Austria w~th
H
=
1760 m) only by 0,83
%.
Strictly speaking: the connpressibility converts the pressure term of the specific energy from
p/~
into
Jtfpig
and requires the introduction of a change of internal energy
e
into thc head
(1.6-
1).
Neglecting
I1
any heat transfer
i11
the machine, thcn ell
-
e,
=
-
fpdo,
[4.26].
I
Once the admissible error of results is prcscribed, compressibility bas to .be accounted for
e.g.,
in efli-
ciency calculation from a certain head on (about
200
m).
It is always required for water hammer cal-
culations, Cap.
8.3.
11.
Surface tension: This is
a
force per unit length acti~ig on the section of the interface
of
a
liquid with gas e.g.? water agaiilst air,
a
=
0,073 N/m.
It
rnay be understood as the
resistance of the
adjacent fluids to increase the contact face in consequence of niolecular
attraction from the interior of the liquid
[5.3].
a
influences the bubble growth rate at the onset of cavitation, if the bubble radius is below
0.1
mm
Ca?illarity effects influence the srnallcst diameter practicable of tappings and manonleter tubes
[5.3].
111.
The
viscosity and resulting classifications of liquids: Liquids are classified by their
shear behaviour.
A
shear stress
r
occurs between adjacent layers slipping against each
other.
r
depends as follows on the strain rate
acjay:
a) Newtonian fluids: Here
7
=
11
dc/dy,
in which
c
is the velocity,
y
the coordinate normal
to
it
and
r]
the dynamic viscosity. For the usual liquid the viscosity drops as temperature
rises.
This ori9inatcs from the increasing distance between the molecules, since the viscous
force is
nlostly caused by molecular attraction.
This "viscous shear stress" appears
in
a Newtonian fluid only, when the flow reginic is laminar.
This
occurs below a definite strain rate and the related Reynolds number (see later). Above this threshold,
the
stead! motion of the fluid has,turbulent velocity fluctuations in and across the main flow direc-
tion superimposed.
Usually the kinematic viscosity is used, defined by
v
=
q/~.
1'
also drops with rising
terrl;
perature, e.g., for water:
at
O°C,
v
=
1,s
10-6m2/s;
at
20°C,
v
=
m2/s; at
70°C
r.
=
0.4
-
m'js.
I;
is therefore anderstandable, that as found
by
.Pieint.rschmidt's
[5.20]
tests. the decisive wall shear stress losses of
a
hydro turbine drop by 25% with
temperature rise from
O0
to
70°C.
This is also true for the turbulent flow regime, since the velocity fluctuations there di
185
i,ppcar
in the Inmiri;~r sublaycr, ncxt to thc wall.
The
wall shcar strcss is the main sourcc
of loss.
b)
Nan-Ne\rtoni.~ri
fluids: JJel-e
r
=
r,
-t
k(2c/?j.)",
ill
which
r,,
is
tllc
yicld sllc:~r stress.
e-g
tooth pastc needs a definite
pressure
to ovcl-comc thc yield stress before
it
pops out
of
the tubc.
k
is
thc
"stiffness
nun~bcr".
It
depends on the amount
of
sl~spended matcrial
in
the liquid. 'Tlir~s tile above may also hold for "rc;ll \wter". Morcovcr thcse fluids havc
a
"memory".
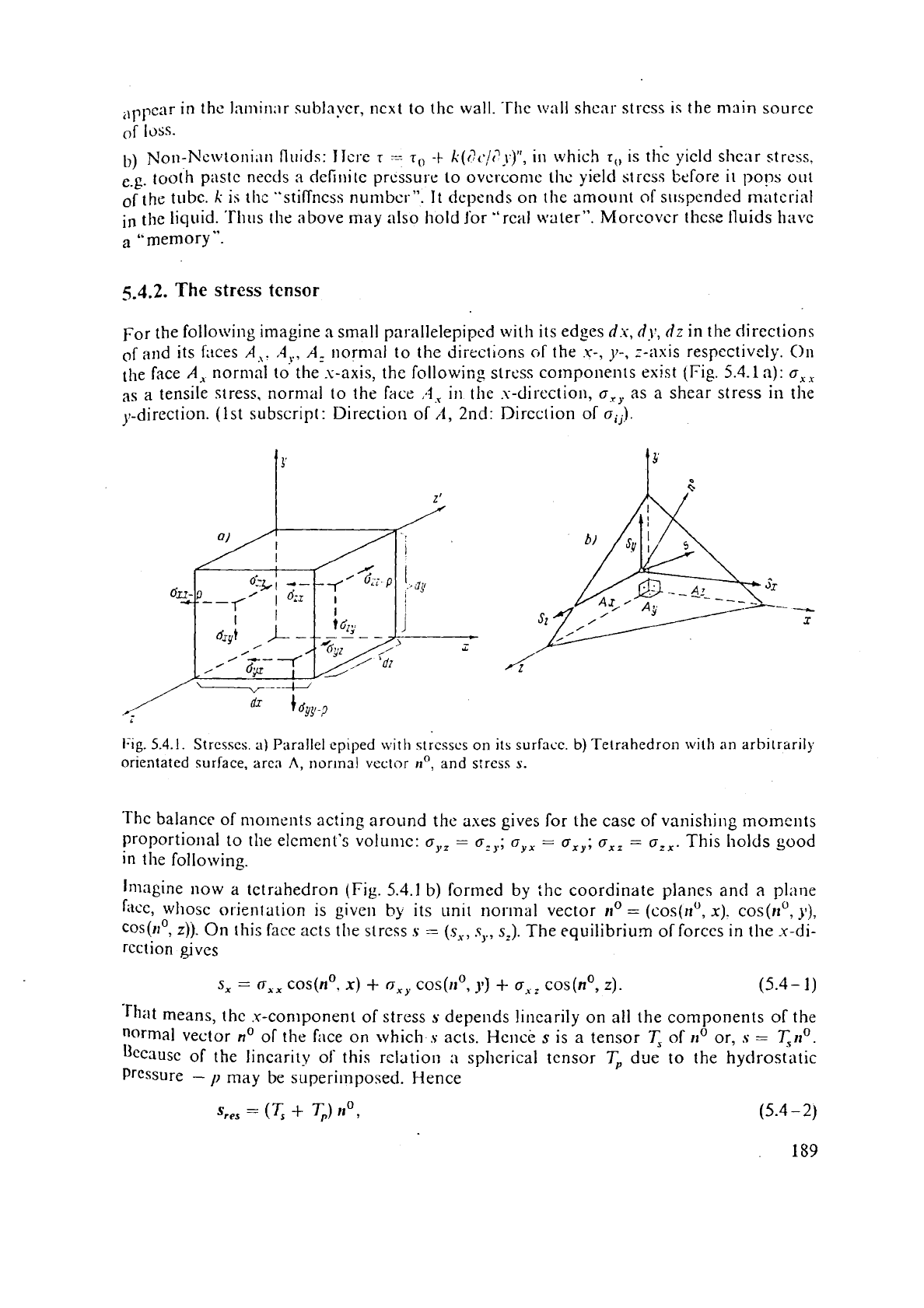
5.4.2.
The
stress tensor
For the followillg imagine
n
small parallelepiped with its edees
d:i,
dj-,
dz
in the directions
of and its Ltces
A,.
,4,,
A:
normal to the direct;ons of the
s-,
y-,
:-asis respectively.
011
the face
A,
normal
to
the x-axis, the following strcss components exist (Fig.
5.4.1
a):
a,,
as
a
tensile stress, normal to
the
face
'4,
in
the
r-direction,
a,,
as a shear stress in the
)#-direction. (1st subscript: Direction of
A,
2nd: Dircciion of
oij)
'
Fig.
5.4.1.
Strcrscs.
a)
Parallel epiped
with
strcsscs
on
its
surfacc.
b)
Tetrahedron
with
an
arbitrarily
orientated surface,
arc3
A,
nonnal
vcctor
11"
and
s!rcss
s.
Thc balance of moments acting around the ases gives for the case of varlistii~lg momcnts
-
proportional to the element's volunlc:
a,,,
=
a,,.; a,,
-
a,,; a,,
=
a:,.
This holds good
in the following.
In~agine now
a
tetrahedron
(Fig.
5.4.1
b)
formed by :he coordinate planes anti
a
plane
fiiicc, whosc orizntation is given
by
its un~t nol-~nal vector
rro
=
(cos(rto,
x).
cos(nO,
J),
cos(nO,
2)).
On this facc acts the strcss
s
=
(s,,
,.,
s,).
The equilibrium of forces in the
x-di-
rection gives
S,
=
cxx
cos(nO,
X)
+
0,
COS(IIO,
yj
+
ox=
cos(nO,
z).
(5.4-
1)
-That
means, thc .Y-conlponent of stress
s
depends lincarily on all the components of the
normal vector no of the face on which
s
acts. Hence
s
is
a
tensor
T,
of no or,
s
=
T,IZ'.
Uccnusc of the linearity of this rclotion
n
spl~crical tcnsor
T,
dge to the hydrostatic
Pressure
-
p
may be superimposed. Hence

u
hl:rc
\,,
,
i.;
11ic rc'hltlti~lg pt.cssiIrc
011
IIIC
[;KC.
riorlii;1I to
rtO,
T,
il11d
.<,
are dcfinccl
by
tl~c
f(;~i!cv..i::g
:cn.;or ma!rix
!n
rc-ility
tl~s
>tress
components
oij
arc duc to viscosity and hence Lippear only
in
a moving fluid,
-
y
:lets
::;so
in
a
sr;itic fll~id
in
consequence of weig!lt and mainly
of
cxchangc of momcntiun due
to
th;
Brc;\\
ni:i:l
nioiccular motion.
Hence
in
agrccn~e~~t
with
cxperiencc and aftcr Pu.sccrl's theorem
[5.3!
at
a
ccr:ain
point and
on
an arbitrarily orien~ed face large relative to
the
molcculcs,
-
p
is
constant.
Accartli;;2 to
a
rule for synlmctric:il tensors
[4.26]
like
T,
and
Tp
the mean value of
tile
sum of normal
stresses
duc
to
rhc
thrce
coordinate planes, r~ormnl to each other, is independent of the orientation
of
those
plsncs.
Accordingly
-This
i~cliic;es also
IJkrs~vrl's
tl~corcm of
an
ideal fluid
with
crij
=
0
and hence
-
p
=
const.
5.4.3.
7'ilc
relation
bctwcen
stress
and
strain
rate
Fro[?i
(5.4-3;
and (5.1-25)
it
is seen that the tensors of stress and strain rate are
srr:rni.~r~cal
ro
thcir r?~ain ciiagcjnal. Under the assumption that the principal
axes
ofboth
rhc
r~nsai
c!ilpsoids
co~r~cide, both the tensors are assumed to be proportional to each
orh2r according !o
T,
=
211
T.,
rl
being the dynamic viscosity.
l.\B.ii!~
t!12
rc.!;~tion
cf~,,.~,(ln
=
TII'
derived
from
(5.4-27)
and
(5.4-2)
the above
pmpor:~o.:,li!t:\.
cf
T,
and
T,
gives
In
11.4
-
27)
compre3sibility was neglected. In
a
real compressible fluid the rate of
str:!in \>risir,ating from pressure
-
p,
being
-
(113)
div
c
is imagined to occur as an
addi-
tion21 str;iir?
rate
ir~
the thrce coordinate directions due to the linear extension rates
aci/ai.
Incorporati~lg this ini,)
t~c,,,,./dn
and
using tensor notation gives the following tzlation
bet\?-esn ibcous stress
G,,
and the strain rate, when neglecting a special term due to
bulk
viscosity
[5.3].
and
employing "the
Xronecker
hijW,
0
for
j
=#
i
and
1
for
j
=
i,
c,,
=
~;(Cc~,?j
i-
2cj/8i
-
(213)
dij div
c).
(5.4-31
A
r2latic.n
of
[his
kind.
without the
Sij
was first postulated
by
Nervier
[5.21]
and
Sto
[5.22]
The
hb:u
toiii;\n relation between shear stress and strain rate,
a,,
=
q?c,/dg,
m
be ccjnsidersd us
n
forzrllnner.
5.4.4.
The
Xavier
Stokes
equ
a
t'
1011
Constituriri2 the equation
of
motiorl for unit mass of
a
real viscous fluid needs
in
additio
to
that
of an ideal fluid,
(5.3-
I),
the stress term
Zp,/ax
+
i?p,li?y
+
dp,/i?z,
wher
190

px
=
(gxxr
Oxr,
ax:).
p,.
=
(c,,,
o,,,
a,,),
p,
=
(a,,,
o,,,
uIZ)
are the stress vectors in thc
1111-cc coordinate plancs. Hence thc equation of motion in tcnsorial nlnlltler is
~ntroducing the stress
ajj
from (5.4-7) gives the
Novier
Stokes'
equation for a slightly
compressible fluid (divc
+
0,
from (5.2- 5))
grad
Y,
-
c
x
curl c
+
&/at
-
v(Ac
+
grad(div c))
=
0.
(5.4
--
9)
5.4.5.
Boundary layer theory
In a plane, incompressible, steady flow without gravity, the x-component of
(5.4
-9)
reads
It is known by experience, that the plane flow around a smoothly curved body shows
viscous effects only in
the so-called "boundary layer" close to the wall (Fig. 5.4.2aj.
According
to
Prandrl
[5.23] a flow in the x-direction
is
assumed along the face of this
body. The y-axis is normal to this face. On the surface of
the
body the
fluid
comes to rest.
Within the very thin boundary layer of thickness 6 the velocity reaches the constant value
of
the free flow
C
(U
in Fig. 5.4.2a).
The motion normal to the body nearly disappears. Therefore there is no pressure drop
across the layer. The pressure from outside acts through the layer. Moreover the term
with c, vanishes. In the case of a flow along a plate, now collsidered, the pressure gradiect
of the free flow and hence the term
dpldx
vanishes.
dx
should be of the order of the
distance
x
from the leading edge of the plate. c, and
dc,
should be of the order C. Hence
c,dc,/ax is
of
the order C2/x.
The first viscous term in (5.4- 10) being of the order of vC/x2 can be neglected in com-
parison with the second term which is of the order
vC/b2. Hence only the second and lift11
term in (5.4-
10)
remain, being of thc order C2/x and 11C/d2 respectively. Introducing
a
Reynolds number
Re
=
Cxlv, the boundary layer thickness grows along the plate
according to
6
--
x
Re-'I2. Strictly speaking for laminar flow [5.24]
Example: Given x
=
1 m,
C
=
30
m/s,
v
=
m2/s:
5
=
0,32
.
m.
Hence the wall
shear stress is of the order of
7
-
qC/6. For water with
q
=
Pas:
t
z
100
Pa.
5.4.6.
Flow
in
straight
pipes
5.4.6.1.
General phenomena and laminar
flow
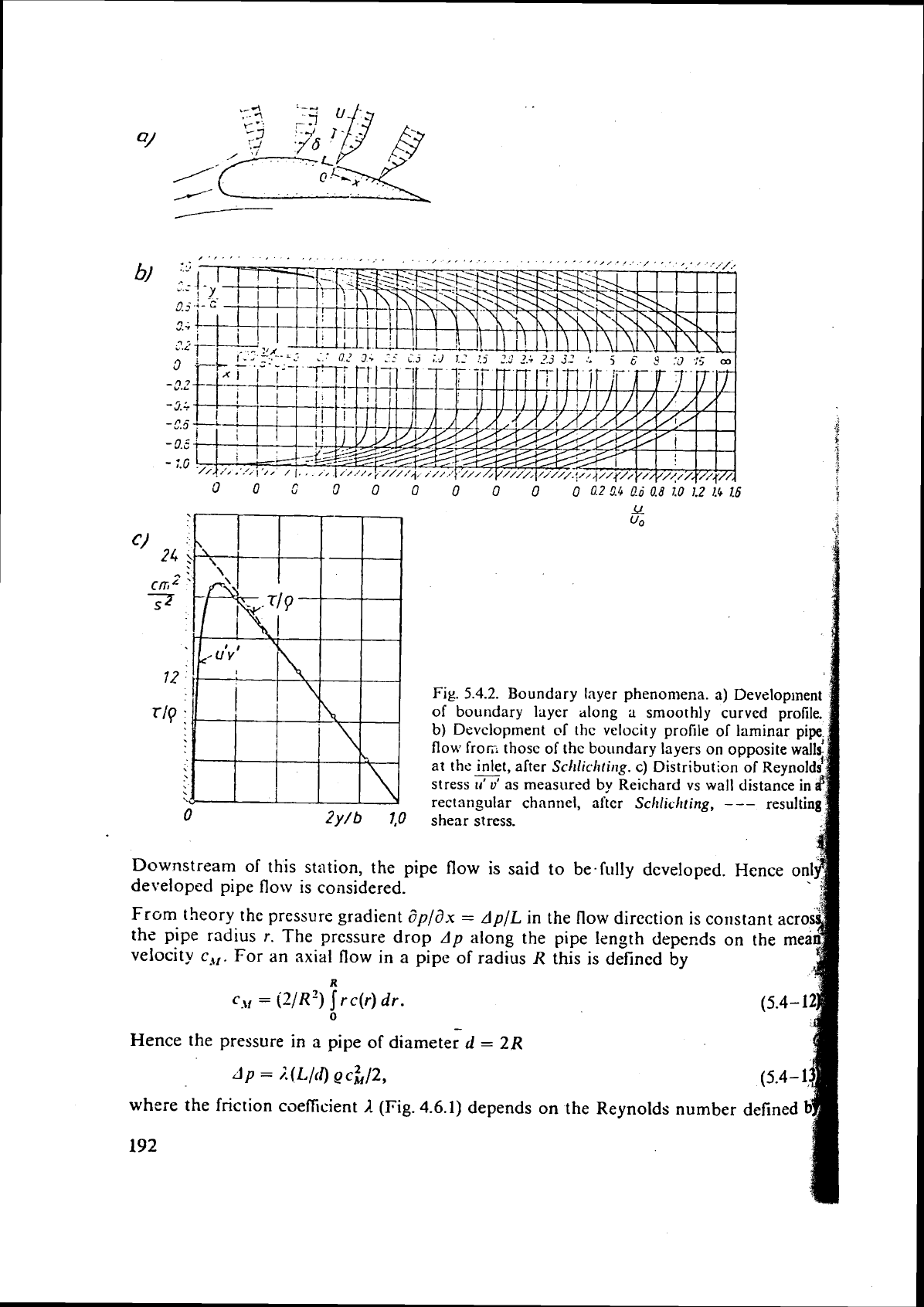
In the case of an internal flow along a straight pipe, the boundary layer grows from the
inlet
up
to the point, at which the boundary layers of oppositely located walls merge.
Downstream
of
this station, the whole pipe is filled with boundary layer. For laminar flow
!his "inlet length" from the pipe inlet to this station depends on the Reynolds number and
IS
of the order of 60 pipe diameters (see Fig. 5.4.2b). For the turbulent fiow regime, this
length is shorter.
,.,.,.
,.
.
.,.
.
.
,
.
. . .
,
.
,..
i
-4
1
3
t
3
0
C
3
0
0
0
0
0
0
0.2
$4
ad
0.8
ZO
1.2
14
Z6
i
u
C)
24
i.
,mi
:
,
',
'\
uo
j
/
U'Y
'
lz:/
r/p
:
b)
Devcloprnent of thc velocity profile of laminar pipe
flow
fro^
thosc of the boundary layers on opposite
wa
at the inlet, after
Scl~lichting.
c)
Distribution of Reynol
stress
u'
as measured
by
Reichard vs wall dis
:bd3d
2y/b
1,0
shear rectangular stress. channel, after
Sclrliclrting,
---
0
Downstream of this station, the pipe flow is said to be-fully developed. Hence on1
developed pipe
flow
is considered.
Faom theory
the
pressure gradient
ap/dx
=
Ap/L
in
the flow direction is corlsta
the
pipe radius
r.
The
pressure drop
dp
along the pipe length depends on
t
velocity
c,,.
For
an
axial
flow
in
a
pipe
of
radius
R
this
is
defined by
R
c.,,
=
(2/R2)
jrc(r)
dr.
0
-
Hence
the
pressure
in a
pipe
of diameter
d
=
2R
Lip
=
i.(L/tl)
gc&/2,
where the friction coefficient
1.
(Fig.
4.6.1)
depends
on
the Reynolds number defined
192
-
I
\
I
I
Fig.
5.4.2.
Boundary layer phenomena.
a)
Developlnent
of boundary layer along
a
smoothly curved profile.

Fro111 the origin of (5.4-
I
I)
it
is realized, that in a frce laminar boundary layer with a
ratio
0,'s
at
a definite station
x
the lieynolds
l lumber
niay
be
undcrstootl as thc
of
mom en tun^
flux into the boundary laycr, of thickness
(5,
to the force due
to
viscous
sllear stress, balancitig it.
This may be extended to pipe flow, when
6
=
d/2 and
7
on the periphery of
a
fluid cyl-
inder,
coaxial to the pipe axis, of radius
r
and length
L,
is replaced by the pressure drop,
balancing this in the s-direction of the pipe axis, according to
7
=
-
Aprl(2
L).
(5.4
-
15)
In the casc of laminar pipe flow \vith
Re
<
2300 and the shear stress
a,,
from (5.4-7), now
,
=
-
11
dc/L;r,
(5.4- 15) givcs a parabolic velocity distribution
c
=
c,[l
-
(r./R)']
after
Hagen
and
Poiselrille
[5.25;
5.261,
where c, is the velocity
011
the pipe centre line. Inserting
this c in (5.4
-
12) yields
c,,
=
c,/2,
which is now linked to
Ap
and
17
by
Inserting this
Ap
in (5.4-
13)
gives for the laminar flow regime the pipe loss coeflicicnt as
a
distinct function of
Re,
namely
1
=
64/Re.
In the transition regime about
Re
=
2300,
1.
depends also on the relative wall roughness and its
character, c.g. sand roughness according to
hTik~iradse
[5.27]
technical roughness as defined by
Slrsclteletzk~~
[5.28],
but also, nftcr tests of
E.
Burka,
Gdansk (Poland) on such eficcts as the arrrplitude
and frequency of wall vibrations. Such tests demonstrate that with
RE
increased the flow becomcs
increasingly unstablc, especinll) through the
layer
close to the
wall,
where strain rate is highest
and
hence also thc tendency to
turbulence.
5.4.6.2.
Turbulent
flow
and
transitior~
Turbulent flow is defined by the fact, that on a time-averaged constant velocity
component
E,
and pressurc
p
are superimposcd corresponding fluctuations
c:
and
p',
the
time-avcraged value of each of wliich is zero. Thus: ci
-
ci
+
ci and
y
=
p
+
p'.
The
intensity of turbulence is defined by
Turbulence is created by the fact, that
abovc a definite strain rate, i.e. dc/?r in the case
of pipe flow, which always occurs first close to
the wall, the fluid elements tlicre try to
cscape to flow regions with lower strain rate, away from the wall. Mass conservation
requires, that fluid particles
01
high velocity more distant from the wall migrate into the
wall zone [5.28].
I)ue to the cross fluctuations, zdjacent flow laminae mix. Thus the
flow
is more uniform
than
a laminar one. This causes also an eschange of momentum, due to the main now,
htween adjacent layers. Thus the so called "apparent shear stress" (after
0.
Rcyr~olds
15-29])
act between them. With c: and c: as velocity fluctuations in the r-and x-directions,
'he
shear stress
rTu
due to turbulence on
a
coaxial fluid cylinder in a pipe reads
Here the bar indicates .a time-averaged value. Since both
thc
velocity fluctuations are
Pro~ortioilzl to the mean pipe velocity
c,,
the shear stress is given by
T,,
=
-
e
kc&, in
which the parameter
k
depends on
Re
and the relative
roughness.

~Iftcr
(5.3
15) and :!ccor.tling to tchts
of
Kc~icl111clr:lr
(Fig.
5.4.2~)
(5.361,
the
resulting
shear
,trcb\
r
oil
a
coaxl;:l fluid cylinticr
i~:
;i
pipe grows lincilrly with the radirls
r.
7
must
bc
split
into
T,,
and
c,,,
duc to viscoi~s cffzcts. Reduction
01'
T,.,,
to
11
and strain rate
dc/d,.
n~:edb the veloc11\ distribution
c.(r).
7
hc lattcr, useful for ca1cul:ition of wall shetir stress
;n
tlic w-c;~licd I;l~liiil;~r hi~blayer,
is
riot
as
simplc as
ill
thc case of laiilir~;~~. flow. 'This holds
truc e\pcci:llly close to the wrill, wlit?re the flow field is strongly influenced by the rough,
ncss structure of the
latter.
I
lcncc in practice thc
sal!
shear strcss in the turbulent regime is expressed similar to
rTU
and
accorcling to tcsts
:vhcre according to tests
of
Blusilrs
[5.31] for
Re
about lo5: ko
=
0,03955;
n
=
4.
Inserting
T,,.
into (5.4-15) with
r
=
R
=
J/2 yields the pressure drop as
dp
=
SkoKe-ll"e(~/d)
cf,
2.
This shows that the general relatior? for the pressuce drop (5.4-13) agrees with
the
I
i~rbulence and equilibrium, when
i
=
8
ko
Re-
'In.
'fi~is is proved
by
the
1.
vs
Re
plot in the turbulent regime for smooth-walled pipes
(T-iz.
4.6.1).
The infli~cnce of wall roughness on due to m;:g~litude and structure
of
obstructions. obc~ously predominating then, can be fourll only by careful investigations,
as
\?.a:,
dnne bj;
XI.
Stt.schrletzky
[5.25].
%
XInny
attempts
haw
been made to describe the distribution of the time-averaged velocity
2
by
one rc1'1tion.
A
simple one reads
i
1
v..itil
cC
;is
the
velocity along the pipe axis and
nt
as a figure depending on
Re.
For
Rr?
=
4
-
lo3.
. .
.i,24
19"
.m
=
6
.
. .
10. Inserting (5.4
-
21) in
(5.4-
12) relates
co
to the
rcean
pipe vclocity
T!.:
apprcui~n!ion
(5.4
-21)
fni!>
on the wall
with
dcidr
=
oo.
A
detailed investigation shows that
a
gc'ncr.ti
la\\
for
the
vclocity disrribution
c(r)
over the whole range
0
<
r
<
R
is not practicable.
At
least
three zones
wrth
trans~tions between them must be distinguished
[5.4], [5.32; 5-33].
-
-
I
tic'
innst essenl~al rntermcd~ate zone is characterized by the fact,
that
the turbulence-induced shear
stress
z,,
nitains its maximum.
-
Hence
Prc~t~:irl
has postulated
T,,
=
const
[5.32].
Further lie assumed
tic'
timc-avcrnged amount
[c:']'
'
of both the fluctrlation
c;
and
c:
in
(5.4-
18)
to bc pro
to
;i
rniult~g
length
I
=
zx,
v
beins the wall distance, and proportional to the cross gradient of
ti,
fly.
Insertins
the
above into
(5.4-
18)
yields, in good agreement
with
tcsts, a logarithm
dlsrirbution of kclocity vs wall distance
y
as
?i'G
=
A
+
B
In(c';
ylv),
\\i;h
A.
B
and
(.",
as empirical
parameters,
which must be adapted to the neighbouring regio
[_c.?:
5.41.
0.
Rc~yrroitis
aqsumed initially, that turbulence is created by instability. For this pur
H.
'4.
L.oret~r:
developed the so-called energy method
15.341.
Since this did not agee with
method oi
snidll
perturbations was developed for two dimensional flow. On this base
[5.3
to
5.371
was the first to calculate thc instability point of a flat plate
[5.37].
This
was
experimentally proved latsr on by wind tunnel tcsts of
Scltubauer
and
Skran~stad
[5.3
Tolltt~irn
found
3
strcnmfunction, which simultaneously satisfies the equation of mot
194

continuity due
to
the fluctuations. Then he
calculated
thc neutral linc for retained fluct~~ntinn
i,mlditude
as
;I
function cf
Rcjnohis
number due
to
the bou~dary Inycr and \irsve length of distortion
p.3;
5.4;
5-35].
Recent
finding5
on boundary layer prediction and
an
exhaustive survey on this sirbjccl came from
~jrrck~nbrorlt
I5.391.
An
important pcrccption is the incrcasc or dccreasc of turbclcncc in thc bound-
ary
laycr by
n
strcamwise dccclcration
or
ncceleralion rcspectively
of
thc adjaccnt
main
flcw
(see
Cap.
9.7).
5.5.
Loss mechanism
due
to
real
flow
in
hydro
tl~rbolnachines
5.5.1.
Some
general
ren~arks
on
loss
in
hydro
turbo machinery
Since all the phenomena in nature are connected with an increase of entropy, each uni-
form motion has the tendency to convert itself by irreversible processes
illto irregular
molecular motion and thereby into waste heat.
Thus, e.g. in a turbine, a portion of energy
first available in a
form convertible into shaft work, is lost for
this
purpose.
This transformation occurs by dissipation mainly in boundary layers
and
wakes
or
zones
of
high vorticity. In certain sections of turbcniachines the fluid possesses
a
larger portio~
of its specific energy as kinetic energy, when compared with positive displacement en-
gines.
A
certain portion of this orderly planned motion is converted into disordered lno-
lecular motion of the fluid. I-lence the loss of the fluid engine is rzlatively large.
This procedl~re: increases the temperature of the fluid and hence its intcrnal energy. It also
increases somewhat the
specific volume of ihe fluid and hence its expnnsicn work
Sp:lu
in
a
turbine.
In
closed loops and high head machines tllz loss results in a measurable rise
of fluid temperature.
5.5.2.
Some
loss
mechanism
of
general character
The dissipation
cb
as one of the essential loss mechanisms in real flow corresponds to the
work
done per unit time by the stresses
a,,
in connection with the rate of strain
c?Ci/?j.
Thus
E5.31
@
=
1
aij(aci/dj) di
djdk
v
7ij
is composed of viscous and apparent
(Rey~zolds')
stress
as
"here
ti
=
time-averaged velocity,
cf
=
velocity fluctuation.
'or convenience the non-linear fluctuating term, only known
(if
any at all) from rnea-
urcinents is replaced by
q,,(aFi/dj
+
ac,/ai),
in which
q,,
is the eddy viscosity. There are
cveral exp;cssions for
q,,,
e.g. that of
van'~riest
[5.40].
^llc
second term of
(5.5-2)
prevails in the practically important turbulent regime.
Only
'1
the laminar sublayer close
tc
thp, wall is the viscous strcss of the same order as the
PParen
t
st rcss
(5.28).
5.5.3.
lntcractiori
of
rn:~ln
flow
2nd
bot11~da1-y
l;~jcr,
stnll
I:llel:.~~ti~i)
I>it\\.t'tri
iil;li11
flo\v
atid
thc
boundary I~JCI. may
GILISC
;I
~1.:111. This is
iI
flow
scparatic)tl from 111c
n;~ll,
;111d may occur Tor ex;ln~plc
in
a difiuscr (draft
tubc)
(Fig.
5.5.1
a).
Hcrc
:i
"tlend
water
rc~iotl" or
"wakc"
pc~~etl-ates bctwccn tlic wall a11d llie ''~nain
flow".
'The mecl1;lnism operates as follows:
It
can be seen from
Fig.
5.5.1
n
that at1 "inflection point" in the "bour~d:~ry layer profilen
Inay caiisc
a
"flo:v ~cp;\iation". This yields
d2c,/dy2
>
0
as a prereqi~isitc for "stall". For
1amin:tr flow the
equilibrium
without inertia terms close to the wall requires
dp/ax
=
c^r!6y, in which
T
is thc shear stress,
x
the streamwise coordinate atld
y
the coordirlate
nortn,ll to the wail. Il~serting
7
=
tjilc,/Jy
gives at constant
q:
i-Iencc
the above iinequality reveals a strcamwise pressure gradient
as
the
proper
prerequisite
for stall together with
r
=
0.
Fig.
5.5.1.
Diffuser flow.
a)
d2cJ
ayZ
>
0
2s
a
colldition for stall.
:
b)
Model
of
2-dimeasional diffuser,',
investigutcd
by
Rennu, Johnston,'
Klinc
[5.41].
c)
Flow
regimes in
a
2-dimensio~~al diffuser according
b):
a
limit of any stall;
a,
line
start of
stnll;
h
line for inception
one side
stall;
c
upper limit of
j
flow;
tl
hysteresis
zone; exampl
also valid for 3-dimensional diffuser
flow without swirl.
d)
Bell-shape
difCuscr.
1
1.5
2
3
1
6 8
10
15
20
30
40
60
1
/A,
5.5.4.
Diffuser
(draft
tube)
flow,
rotating
stall
A
diffuser
(draft
tube)
is
a
duct ivith a diverging cross section
for
the recuperation
oft
kinetic energy
c2;;2
at
it
inlet. I-Iere
a
streamwise pressure gradient occurs due to energ
196
