Пупенцова С.В. Экономика недвижимости в задачах и примерах

Подождите немного. Документ загружается.

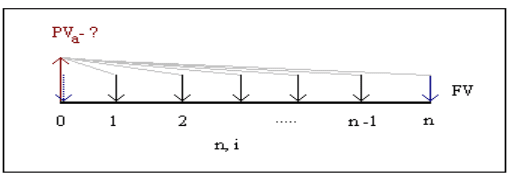
Рис. 1.11.

3. Текущая стоимость мерного потока. Функция

НПЗ ( норма – ставка процента, значение1 –

доход

ех бу-

дущи

неравно

норма;значение1; значение2;…), где

(выплата, платеж) первого года; значение2 – доход (выплата, платеж) вто-

рого года и т.д. данную функцию часто используют для расчета NPV.

Чистая текущая стоимость (NPV) – дисконтированная стоимость вс

х денежных потоков, минус

начальные инвестиции.

CNPV

)1()1(

+−

∑

(9),

где С

– начальные инвестиции, I

– ежегодный доход (например, NOI), V

– доход

от продажи объекта рсии).

Например, чистый операционный доход перво будет равен

100 тыс.

у.е., и будет ваться на 2 тыс. у.е. в год, лет эксплуатации

объект будет продан за 1000 тыс. у.е., найти чистую текущую стоимость проекта,

если требуются начальные инвестиции в сумме 800 тыс. у.е., а норма дисконти-

рования равна 10%

текущую стоимость: НПЗ (0,1;

100;102;104;1106) =1009 тыс. у.е., см. рис.1.12.

(реве

го года

увеличи после 4

Для определения NPV можно воспользоваться функцией НПЗ, для этого

создается массив положительных

денежных потоков (100;102;104;1106) и, имея

ставку дисконтирования, можно найти

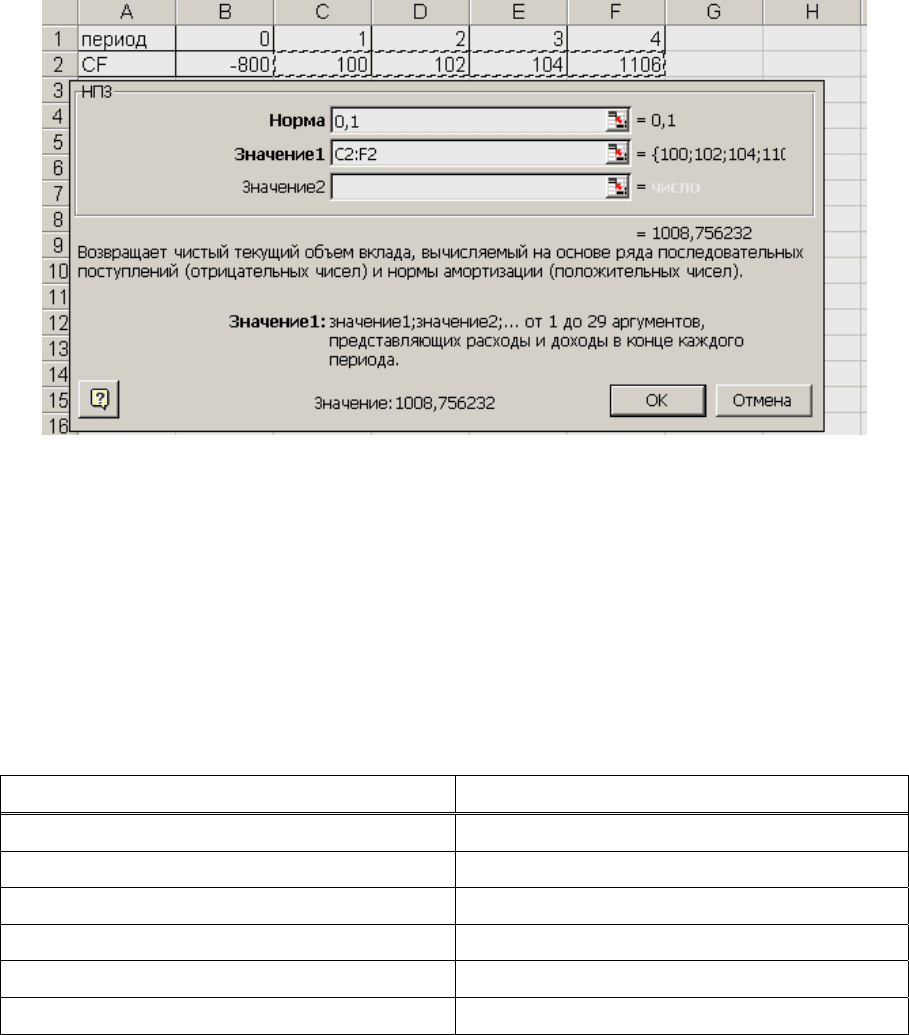
Рис.1.12

Тогда NPV=1009-800=209 тыс. у.е.

(Внимание! В справке Excel ошибка: для расчета NPV предлагается. НПЗ

(0,1; -800;100;102;104;1106)=190, что не соответствует расчету по формуле:

NPV=-800+100/(1+0,1)+102/(1+0,1)^2+104/(1+0,1)^3+1106/(1+0,1)^4=209).

Соотве тствие финансовых функций EXCEL XP и EXCEL 98, 2000

Таблица 1.4

EXCEL XP, 2003 EXCEL 98, 2000

ПС ПЗ

БС БЗ

ПЛТ ППЛАТ

ЧПС НПЗ

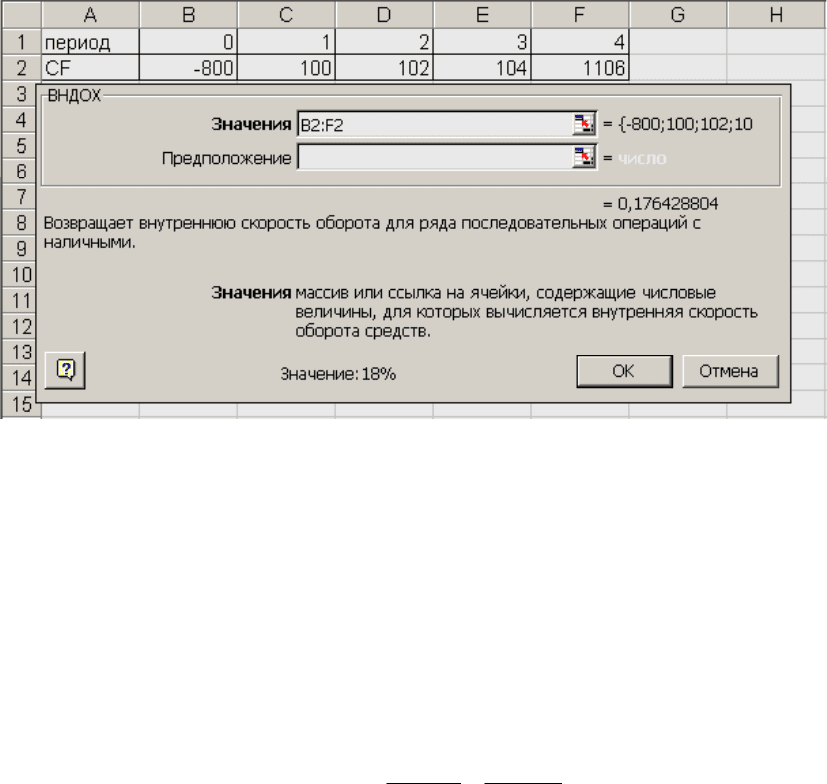
ВСД ВНДОХ

СТАВКА НОРМА

Схема погашения самоамортизирующегося кредита, например, для креди-

та суммой 3170 у.е., выданного на 4 года под 10% годовых, будет сле-

1.6. Различные схемы погашения кредита

выглядеть

дующим образом (см. табл.1.5 и рис. 1.13).

кр

начало

ж,

у.е.

Выплата Погашение основной

суммы долга, у.е.

Остаток основной

суммы долга, у.е.

Таблица 1.5.

Год Сумма на Плате

едита процентов

1 3 170 1 000 317 683 2 487

2 2 487 1 000 249 751 1 736

3 1 736. 1 000 174 826 909

4 909 1 000 91 909 0

Р 3. С пога самоамортизирующегося креди

до

окончания срока кредита, при погашении кредита до истечения срок

цы 3 о р 90 од –

909

Функция (ставка; кол_пер; ; нач_период; кон ;тип)

звол чис сум

которая выплачена или будет ачена по

кредит в интервале между дву ериодами: » до онечного».

Величина кредита может быть только положительной. Последний аргумент

функции ОБЩДОХО 0 или 1 и является

обязат

суммы долга на конец 2-го года (остаток по кредиту – V

), то есть кредит не бу-

ис.1.1 хема шения та.

Остаток по кредиту рассчитывается очень часто при продаже объектов

а. Из табли-

видн , что остаток по к едиту на 2-й год равен 826+ 9=1735, на 3-й г

у.е.

ОБЩДОХОД нз _период

по яет вы лить му,

выпл

у мя п от «Начального «К

Схе ма погашения самоамортизирую

(с равными платежам

щегося кредита

и)

600

12 4

период

Сумма, у.

800

1000

1200

е.

400

погашение основ аной суммы долг нач оцентыисленные пр

Д - тип выплаты принимает значение

ельным. Например, требуется определить выплаченную часть основной

суммы долга (суммы кредита) между 1 и 3 периодами: ОБЩДОХОД

(0,1;4;3170;1;3;0) = 2260. Например, требуется

определить остаток основной

дет выплачиваться с 3 по 4 периоды: ОБЩДОХОД

ПЗ(0,1;2;1000)=1735 у.е.

порядковые номера которых обозна-

чаютс

то в р

выплат основной суммы долга

приве

сновной

(0,1;4;3170;3;4;0)= 1735 или

Примечание. Функции ОБЩПЛПАТ и ОБЩДОХОД позволяют вычислить

выплаты между двумя любыми периодами,

я как Нач_период и Кон_период. Если эти величины равны между собой,

езультате получается выплата за один период. Выплату процентов за один

период можно получить также функцией ПЛПРОЦ, а выплату основной суммы

долга за один период – функцией ОСНПЛАТ.

Схема погашения кредита методом равных

дена в таблице 1.6.

Таблица 1.6.

Год Сумма на Платеж, Выплата Погашение основной Остаток о

кредита

начало у.е.

процентов

суммы долга, у.е. суммы долга, у.е.

1 3 170 1 110 317,00 792,5 2 378

2 2 378 1 030 237,75 792,5 1 585

3 1 585 951 158,50 792,5 793

4 793 872 79,25 792,5 0

кредита

ата Погашение основной

суммы долга, у.е.

Остаток основной

суммы долга, у.е.

хема погашения кредита шаровым платежом приведена в таблице 1.7.

Таблица 1.7.

Год Сумма на

начало

Платеж,

у.е.

Выпл

процентов

1 3 170 317 317 0 3 170

2 3 170 317 317 0 3 170

3 3 170 317 317 0 3 170

4 3 170 3 487 317 3 170 0

1.7. Эффективная процентная ставка

Эффективной процентной ставкой, соответствующей данной процентной

ставке, называется ставка сложных процентов, эквивалентная процентной ставке

и не зависящая от срока применения этой ставки. Формула для расчета:

1)1( −+=

эффект

(10)

где i – номинальная ставка (годовая); q - число начислений в году (если квар-

тально, то q=4; если ежемесячно, то q=12).

ЭФФЕКТ(номинальная_ставка;периодов_в_году). Замечания: если эта

функция недоступна, следует установить надстройку "Пакет анализа", а

затем подключить ее с помощью команды Надстройки меню. Аргумент перио-

дов

нальн

б) ЭФФЕКТ(10%;4) = 10,

в) ЭФ

на количество месяцев в году 37,16×12 = 445,96 у.е. (на рис. 1.14

соотв

_в_году «усекается»

до целого. Обратная функция, которая возвращает номи

ую ставку по эффективной, – НОМИНАЛ.

Например, банк выплачивает по вкладам 10% годовых. Какова реальная

доходность вкладов в этом банке при следующих видах начисления процентов:

а) ежемесячно; б) ежеквартально; в) по полугодиям; г) непрерывно?

Решение: а) i

эффект

=(1+0,1/12)^12-1=0,1047 или ЭФФЕКТ(10%;12) = 10,47%;

38 %;

ФЕКТ(10%;2) = 10,25%;

г) ЭФФЕКТ(10%;365) = 10,52%

Например, требуется определить годовой платеж по кредиту, если извест-

но, что сумма кредита 1000 у.е., ставка 20% годовых, срок погашения 3 года, на-

числение процентов ежемесячно.

Решение. Ежемесячно надо будет погашать сумму, равную взносу на амор-

тизацию единицы, при 20%/12 и сроке погашения 3×12 месяцев – I

m12

= 37,16

у.е., но в задаче требуется определить годовой платеж. Просто умножить ежеме-

сячный платеж

етствует меньшей годовой выплате) было бы некорректно. Более правиль-

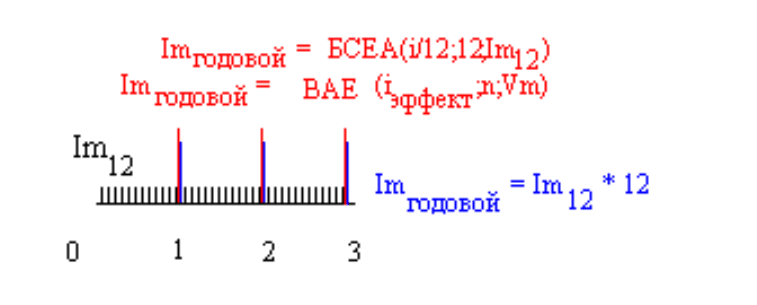
но следует пересчитать двенадцать ежемесячных платежей на конец года по

функции будущей стоимости аннуитета (БСЕА), используя ставку процента

20%/12, период 12 месяцев и выплату – 37,16, тогда годовой платеж равен 489,2.

нии процентов

% и сроке погашения 3 года – 489,20 у.е. (не учтен-

ная го

дач

ет.

50= 304 у.е. или БЗ(0,04;5;;-250;)=304

Задача 2. К дью 16 га с рас-

четом может его продать по 1000 у.е. за га и получить до-

цену за весь массив можно

соглашаться?

Решение: Разумный покупатель не заплатит сегодня суму

большую, чем

текущая стоимость цены земельного массива, по которой он сможет его продать

через 5 лет. Выбираем коэффициент ТСЕ при 20% и 5 годах по формуле (2), рав-

ный 0 ная цена за массив, на которую следует соглашать-

ся, ра ПЗ(0,2;5;;16000;)

лжен платить за аренду помещений по 20000 у.е

. в

Рис. 1.14. Схема нахождения годового платежа по кредиту при ежемесячном начисле-

Второй способ нахождения годового платежа можно, если сначала рассчи-

тать эффективную ставку, а затем вычислить годовой платеж по формуле взноса

на амортизацию единицы (ВАЕ): эффективная ставка – 21,94%, годовой платеж

по кредиту, при ставке 21,94

довая разница между выплатами 43 у.е. и это для кредита

в 1000 у.е.).

1.8. Примеры решения за

Задача 1. Цена 1 кв. м для офисных помещений составляет 250 у.е. и еже-

годно повышается на 4%. Определите стоимость 1 кв. м офиса через 5 л

Решение: Требуется определить будущую стоимость, выбираем коэффици-

ент БСЕ при 4% и 5 годах по формуле (1), равный 1,2167. Цена 1 кв. м через 5

лет будет

равна 1,2167×2

омпания приобретает земельный массив площа

на то, что через 5 лет с

ход в размере 20% годовых. На какую максимальную

,4019, тогда максималь

вна 0,4019×1000×16=6430 у.е. или

Задача 3. Арендатор до

год. О у вперед за 5 лет. Определите сумму, ко-

торую ть, если приемлемая для арендодателя годовая

ставка

из пяти выплат по 20000 у.е. Выбираем коэффициент ТСЕА по фор-

муле

5320, тогда сумма, которую следует запла-

тить ,5320×20000=50640 у.е. или

ПЗ(0,2

з 6 лет отремонтировать фасад здания.

Для э а счет в банке по 1000 у.е. Банк начисляет по

полагать компания

на

мо

елить будущую стоимость аннуитета по форму-

ле (6)

ма стоимостью 20000 у.е. предоставлена рас-

срочк

находим коэффициент взноса амортизации еди-

ет равен

0,3198×20000=6396 у.е. или

ППЛА

1. Гра

н хотел бы внести арендную плат

ему необходимо заплати

процента равна 28%.

Решение: Требуется найти текущую стоимость потока арендных платежей

состоящих

(5) для 28% и 5 лет, он

равен 2,

арендатору сегодня за 5 лет вперед, равна 2

8;5;20000;)=50640 у.е.

Задача 4. Компания планирует чере

того она ежегодно переводит н

вкладам 12% годовых. Определить, какой суммой будет рас

мент ремонта фасада.

Решение: Требуется опред

: 8,1152×1000=8115 у.е. или БЗ(0,12;6;-1000;)

Задача 5. При покупке до

а на 5 лет. Определить ежегодные платежи при ставке 18% в год.

Решение: По формуле (8)

ницы, равный 0,3198, тогда платеж буд

Т(0,18;5;-20000;)

1.9. Тесты для самостоятельной подготовки

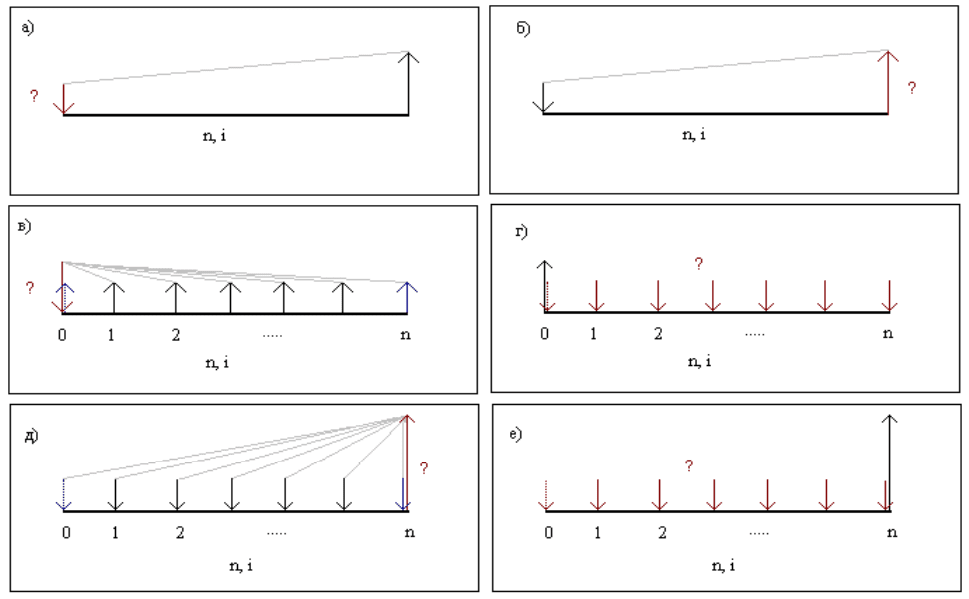
Тесты первого уровн

фическое изображение соответствует функции

а) текущая стоимость;

б) текущая стоимость аннуитета;

в) будущая стоимость;

аннуитета;

ор фонда возмещения.

читывается:

) фактор обычного аннуитета для потока доходов, укороченного на 1 пе-

риод и добавить к нему 1;

б) фактор обычного аннуитета для потока доходов, увеличенного на 1 пе-

риод и добавить к нему 1;

в) фактор обычного аннуитета для потока доходов, укороченного на 1 пе-

риод и отнять от него.

4. Фактор фонда возмещения показывает:

а) каким

должны быть равновеликие периодические платежи при выбран-

ной ставке процента для того, чтобы по окончании всего срока кредит был

полностью погашен;

б) какими должны быть равновеликие периодические платежи при вы-

бранной ставке процента для того, чтобы по окончании всего срока на сче-

ту аккумулировался 1 доллар.

стоимость единицы;

тета;

г) будущая стоимость аннуитета;

д) взнос на амортизацию;

е) фактор фонда возмещения.

2. Какая функция является обратной величиной накопленной (будущей) суммы

единицы?

а) текущая стоимость единицы;

б) текущая стоимость единичного

в) будущая стоимость единичного аннуитета;

г) взнос на амортизацию единицы;

д) факт

3. Текущая стоимость авансового аннуитета расс

5. Какая функция является обратной величиной

фактору фонда возмещения?

а) текущая

б) текущая стоимость единичного аннуи

в) будущая стоимость единицы;

г) будущая стоимость единичного аннуитета;

д) взнос на амортизацию единицы;

6. Есл 1

у.е., т ений? Ставку процента

10%, е.

8. Тре н ывать ежегодно, чтобы че-

ез 5 лет получить 1 у.е., при норме 10%. Изобразите графически решение дан-

ной задачи.

9. Ука

, изображенных на рисунке задания 9,

функц

и объект недвижимости будет приносить ежегодно в течение 3-х лет по

о как найти текущую стоимость будущих поступл

можно принять равной10%. Напишите формулу и найдите ответ по таблице

сложных процентов.

7. Определите платеж по кредиту на сумму 100 у.е., выданного на 5 лет

, под

начисление процентов ежегодно

буется определить, какую сумму ужно отклад

жите, какие функции указаны на рисунке.

10. Определите для каждой из функций

ию Excel.

11. Какое утверждение верно на Ваш взгляд

а) будущая стоимость единицы всегда равна текущей стоимости;

б) будущая стоимость единицы меньше текущей стоимости;

ая стоимость единицы может быть равна, может быть больше, а

итета? Обоснуйте ответ.

13. От

1.10. Задачи для самостоятельной подготовки

риода.

ету через 5 лет при

ставке банка, равной 15% годовых, и еже-

месяч

сможет продать его по 1600 у.е. за га и получить до-

в) будущая стоимость единицы больше текущей стоимости;

г) будущ

может быть меньше текущей стоимости единицы.

12. Какое значение больше: будущая стоимость единицы или будущая стоимость

единичного анну

метьте эффективную ставку процента за квартальный период накопления:

а) (1+i/4)

n x4

–1; б) (1+i/4)

–1; в) (1+i/4)

;

г) (1+i/4)

–1; д) (1+i/4)

n x4

; е) (1+i)

-1;

Если в задаче нет дополнительных указаний, то предполагается, что расче-

ты производятся по схеме сложных процентов и платежи вносятся в конце рас-

четного пе

Задача 1. Накопление на вкладе осуществляется по схеме сложных про-

центов. Построить график ежегодных изменений накопленной суммы при задан-

ной норме 10% годовых

, величине вклада – 1000 у.е. и количестве периодов - 10

лет.

Задача 2. Цена 1 кв. м для офисных помещений составляет 220 у.е. и еже-

годно повышается на 4%. Определите стоимость 1 кв. м офиса через 5 лет.

Задача 3. На банковский счет был внесен вклад в размере 1000 у.е. Какая

сумма будет на сч

ном начислении процентов ?

Задача 4. При рождении ребенка родители положили в банк 1000 у.е. под

14% годовых с ежемесячным начислением процентов. Определить сумму вклада

к совершеннолетию (18 лет) ребенка.

Задача 5. Какую сумму следует сегодня положить на счет под 10% годо-

вых, чтобы через 10 лет получить 110 000 у.е.

Задача 6. Компания приобретает земельный массив площадью 10 га с рас-

четом на то, что через 5 лет