Презентация - Семенкин Е.С. Методы оптимизации
Подождите немного. Документ загружается.


Такимобразом, врезультатепоследовательногопрохождениявсехэтаповотконца
кначалуопределяеммаксимальноезначениевыигрышаза n шаговидлякаждогоизних
находимусловнооптимальноеуправление.
Чтобынайтиоптимальнуюстратегиюуправления, тоестьопределитьискомое
решениезадачи, нужнотеперьпройтивсюпоследовательностьшагов, тольконаэтот
разотначалакконцу. Аименно - напервомшагевкачествеоптимальногоуправления
u
1
*
возьмемнайденноеусловнооптимальноеуправление U
1
0
. Навторомшагенайдем
состояние X
1
*
, вкотороепереводитсистемууправление u
1
*
. Этосостояниеопределяет
условнооптимальноеуправление U
2
0
(X
1
*
), котороетеперьбудемсчитатьоптимальным
(u
2
*
). Зная u
2
*
, находим X
3
*
= u
2
*
(X
2
*
), азначит - определяем u
3
*
= U
3
0
(X
2
*
), ит.д.В
результатеэтогонаходимрешениезадачи, тоестьмаксимальновозможныйдоходи
оптимальнуюстратегиюуправления U*, включающуюоптимальныеуправленияна
отдельныхшагах (u
1
*
, u
2
*
,...,u
n
*
).
Такимобразом, мырассмотрелинахождениерешениязадачидинамического
программированиявобщемвиде. Этотпроцессявляетсядовольногромоздким, поэтому
ониспользуетсяобычносприменениемЭВМ. Отметимтакже, чтоизложенатолько
идея, котораядолжнабытьреализованавтомилииномвидедлякаждогочастного
случаяидалеконевсегдаочевидно, какэтосделать.

Задача о минимизации расхода горючего самолетом
при наборе высоты и скорости
Пустьсамолет, находящийсянавысоте Н
0
иимеющийскорость V
0
должен
поднятьсянавысоту Н
k
ниметьскорость V
k
. Известенрасходгорючегопри
подъемесамолетаслюбойвысоты H
1
налюбуювысоту Н
2
> Н
1
при
постояннойскорости, атакжерасходгорючегоприувеличениискоростиот
любогозначения V
1
долюбогозначения V
2
> V
1
принеизменнойвысоте.
Найтиоптимальноеуправлениенаборомвысотыискорости, прикотором
общийрасходгорючегоминимален.
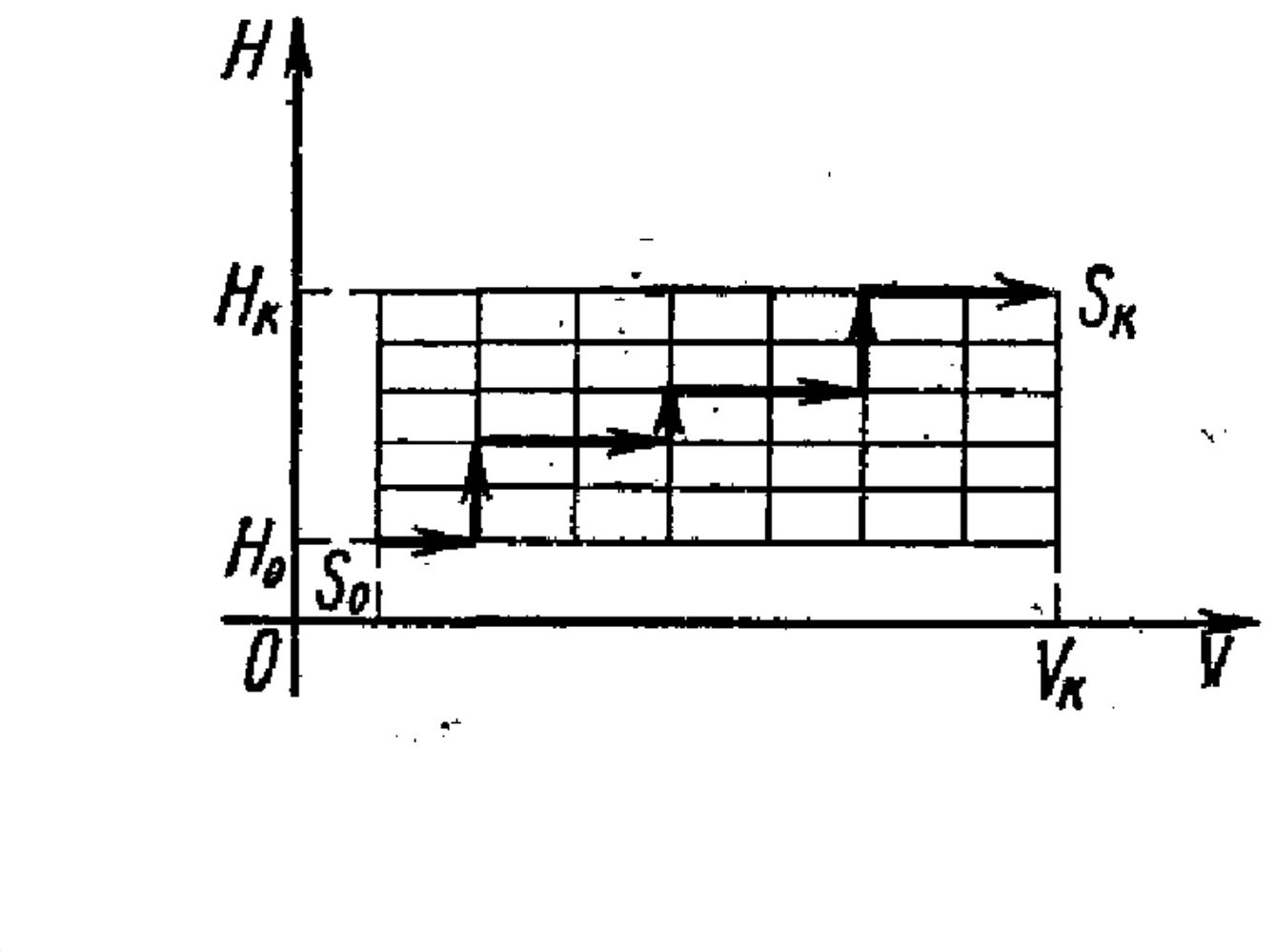
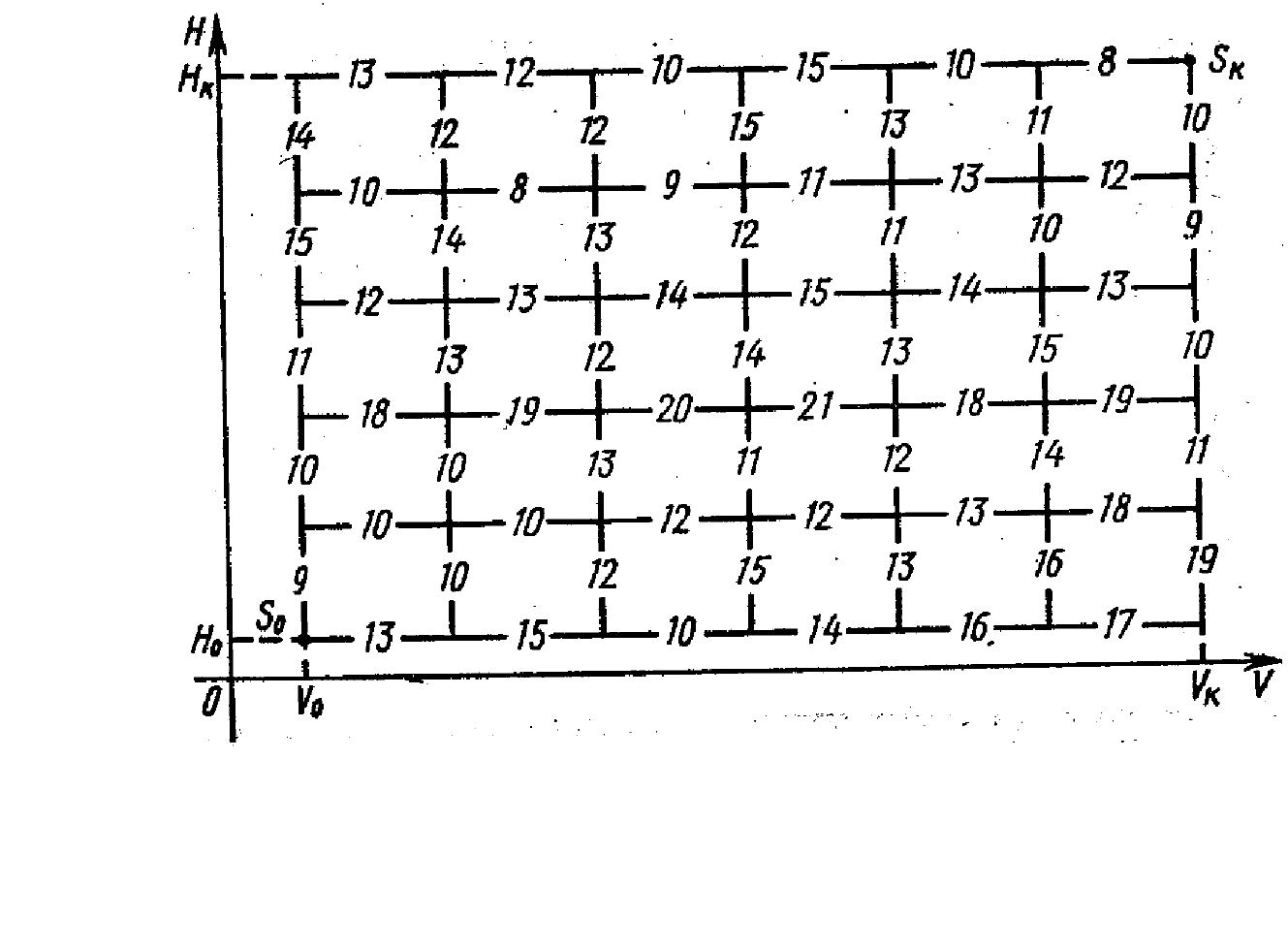
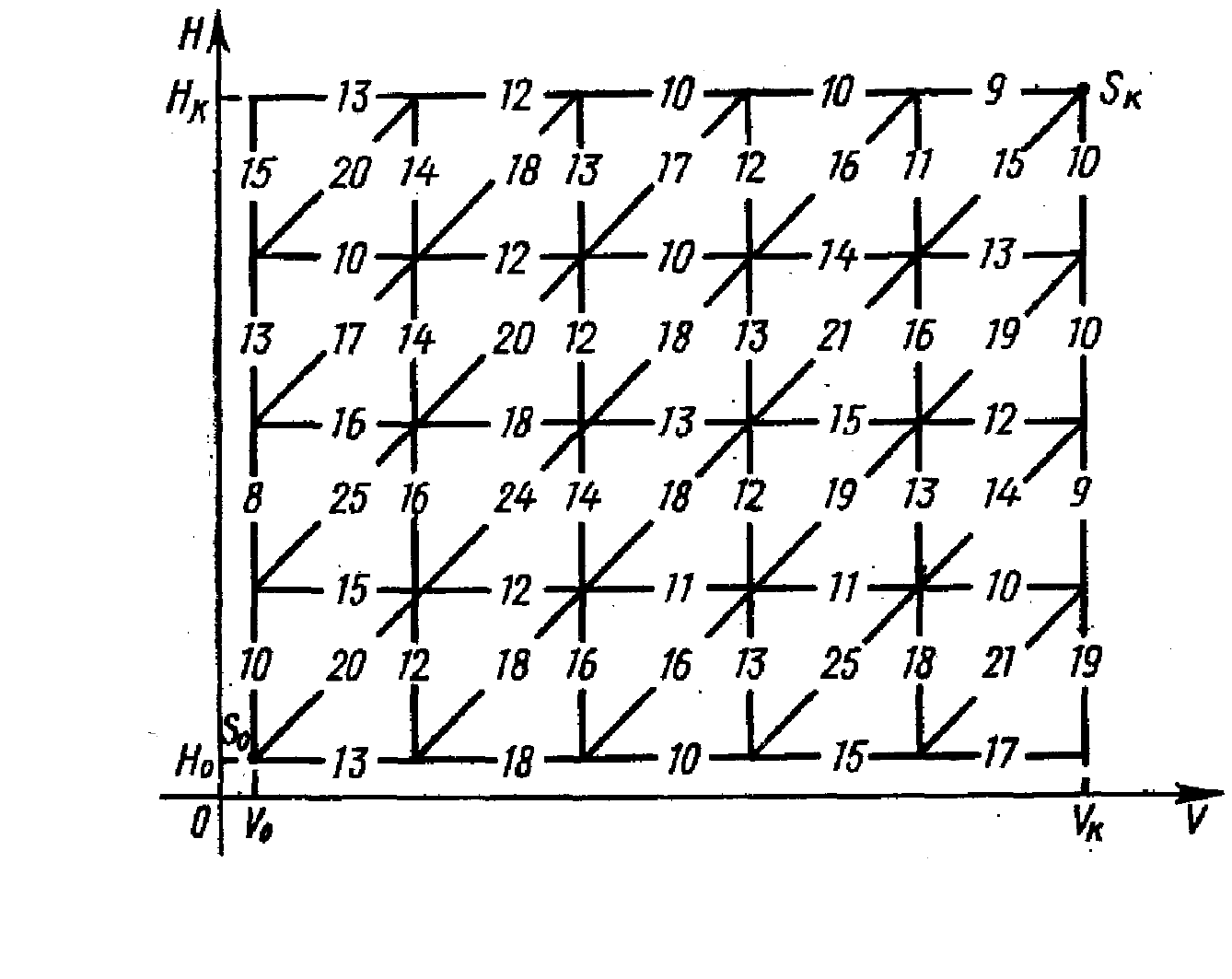
Изусловияследует, чтосостояниефизическойсистемы S (самолета)
характеризуетсядвумяпараметрами: скоростью V ивысотой Н. Поэтому
решениебудемискатьнаплоскости VOH, аточнеенаограниченномпрямыми
V=V
0
, V=V
k
и Н=Н
0
, Н=H
k
прямоугольнике, которыйиявляетсяобластью
допустимыхсостояний. Начальное S
0
(V
0
, Н
0
) иконечное S
k
(V
k
, H
k
) состояния
вполнеопределены, какдветочки S
0
и S
k
наплоскости (см. рисунок).
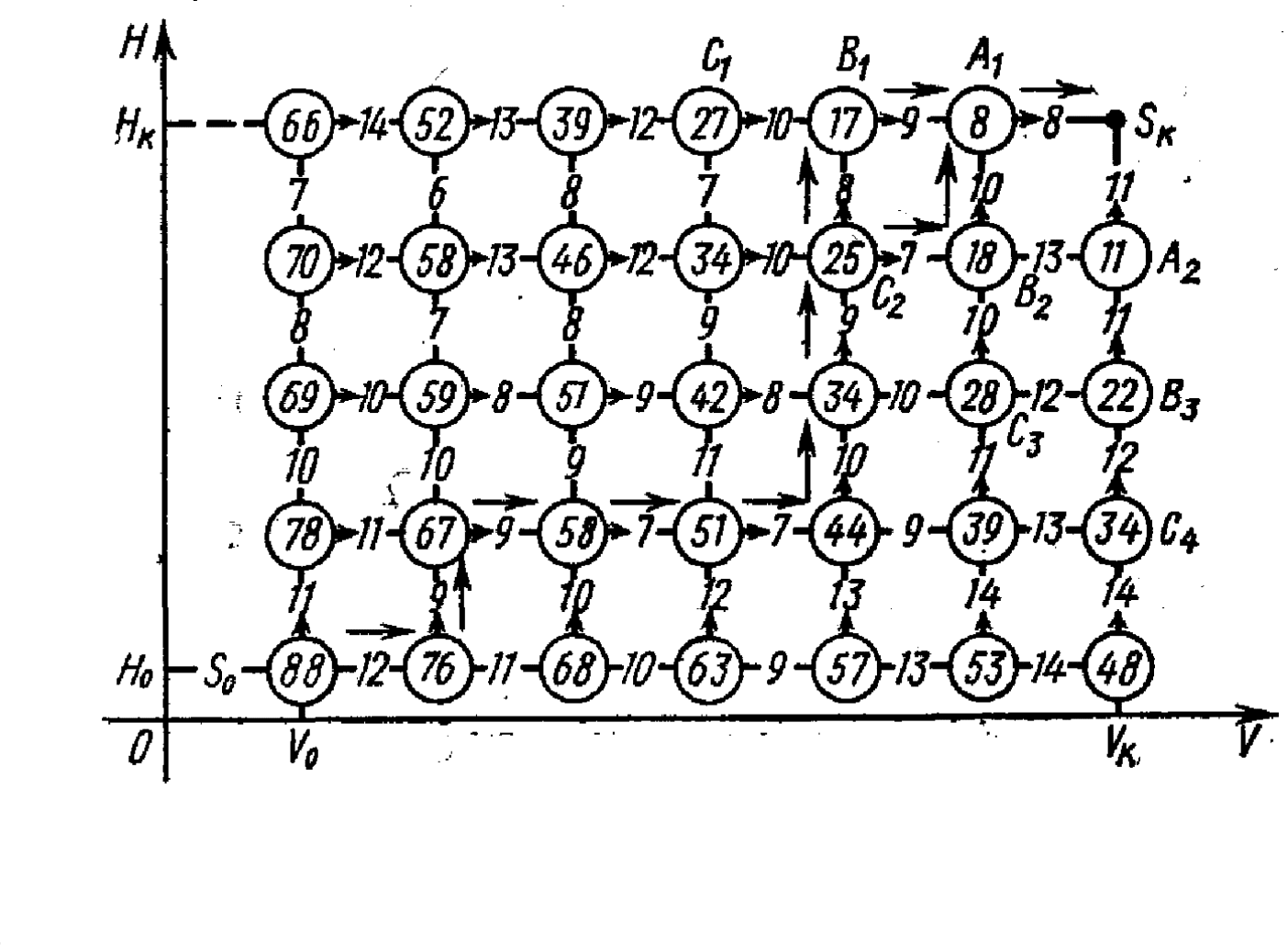
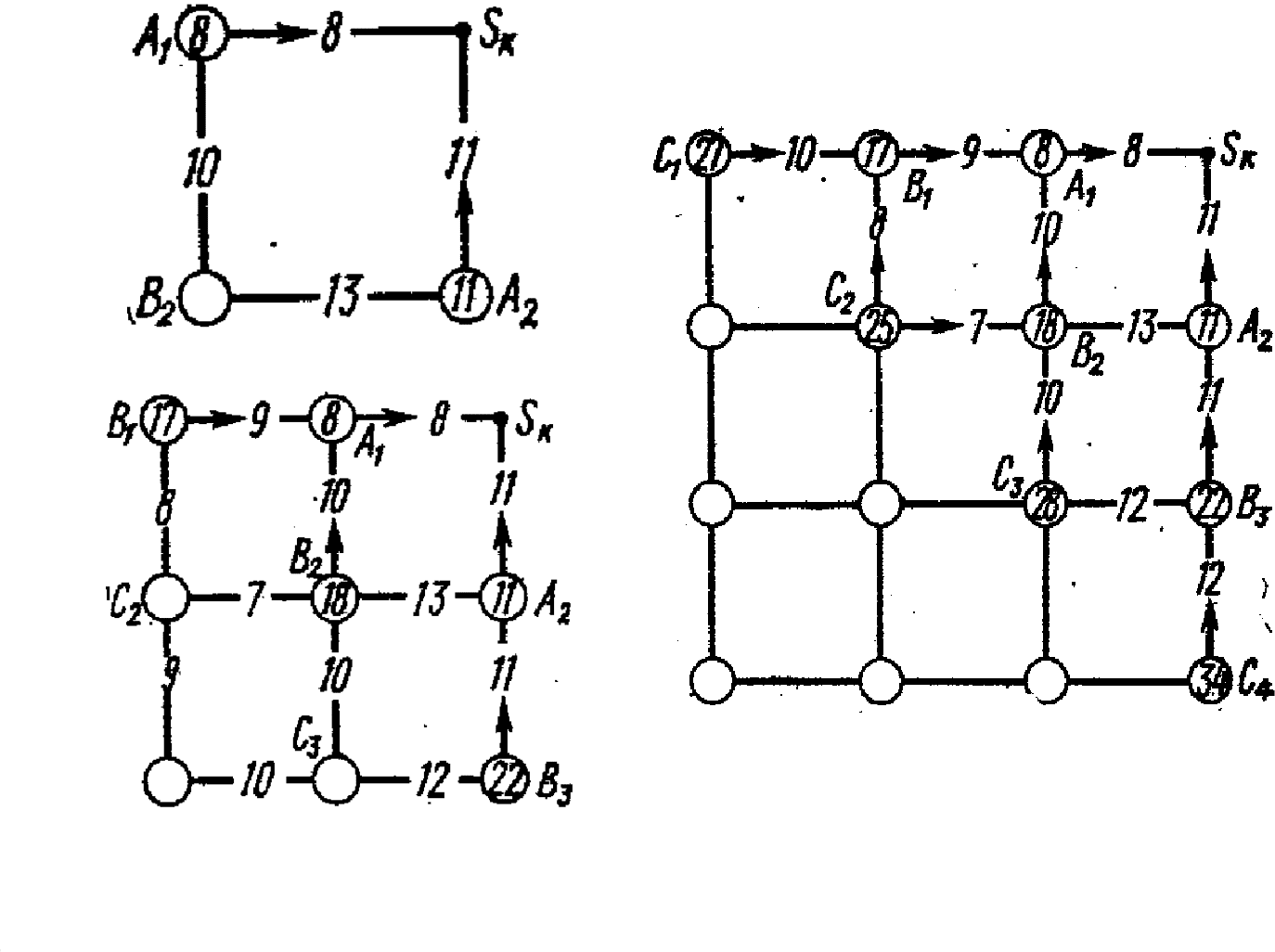
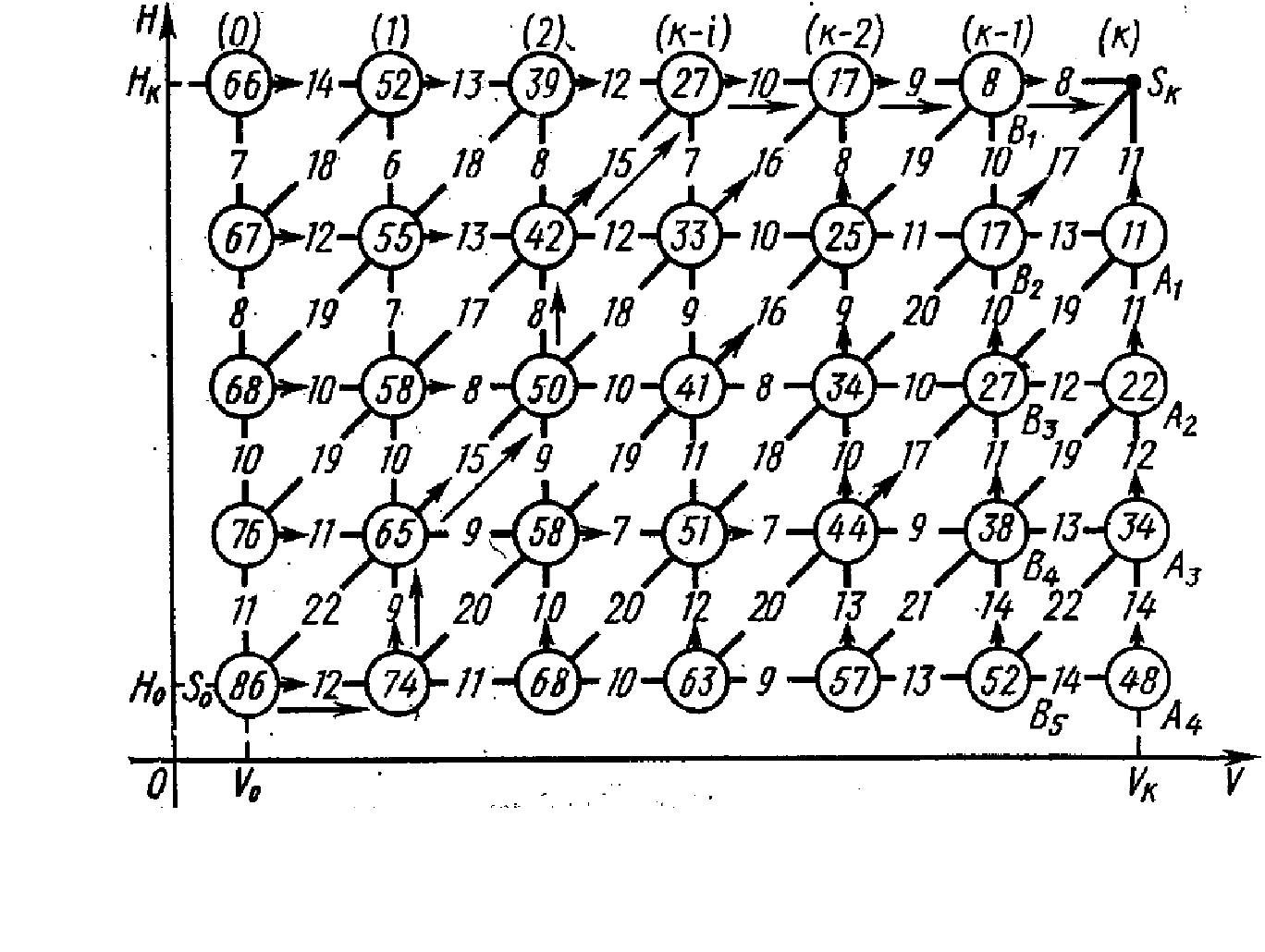

Взаимосвязь между различными подходами к решению задач
динамической оптимизации
Классическаязадачавариационногоисчисленияявляетсячастным
случаемзадачидинамическогопрограммирования, вкоторойуправляющими
параметрамиявляютсяскоростиизмененияфазовыхкоординатвовремени,
причемназначенияуправляющихпараметровненакладываетсяникаких
ограничений. Изнеобходимогоусловиядинамическогопрограммирования –
выполнения уравнения Беллмана – выводятся необходимые условия
вариационного исчисления – уравнения Эйлера, Лежандра, условие
ВейерштрассаиусловияВейерштрасса-Эрдманадляточкиизлома.
Аналогичнымобразом, классическаязадачавариационногоисчисления
является также частным случаем задачи оптимального управления.
Поэтому с помощью принципа максимума Понтрягина (необходимое
условиеоптимальногоуправления) можновывестинеобходимыеусловия
вариационногоисчисления (уравненияЭйлераит.д.).

Между принципом максимума и динамическим программированием,
представляющими собой два подхода к решению общей задачи управления,
существуюттесныевзаимосвязи. Вчастности, выражение, стоящеевфигурных
скобкахвуравненииБеллмана, представляетсобойфункциюГамильтона. Это
уравнение включает отыскание максимума функции Гамильтона относительно
управляющих параметров, принадлежащих области управления. То же самое
требуетсясделатьсогласнопринципумаксимума. Изконечногограничногоусловия
дляуравненияБеллманавытекаетконечноеграничноеусловиедлясопряженных
переменныхвпринципемаксимума.
Таким образом, при выполнении решения по методу динамического
программирования, аименнопривыполненииуравненияБеллманаиграничного
условиядляэтогоуравнения, выполняютсяиусловияпринципамаксимума. Однакоиз
принципамаксимуманевытекаетвыполнениеуравненияБеллмана, посколькувэтом
случаенетребуетсявводитьпредположениеонепрерывнойдифференцируемости
функцииоптимальногоповедения.
Крометого, причисленномопределенииоптимальныхуправленийэтидва
методапредставляютсобой весьмаразличные подходыкдинамическойзадаче
оптимизации: динамическое программирование приводит к нелинейному
дифференциальномууравнениювчастныхпроизводных, а принципмаксимума – к
двум
системам
обыкновенных
дифференциальных
уравнений
.
