Презентация - Семенкин Е.С. Методы оптимизации
Подождите немного. Документ загружается.


Необходимоеусловие 4.
Длятогочтобыфункционал (40) достигалнафункции y(x)∈C
1
[a;b] слабого
экстремума, необходимо, чтобыэтафункцияудовлетворялауравнениюЭйлера
иусловиямтрансверсальностидлязадачиБольца
, . (41)
Условия (41) используютсядляопределенияпостоянных C
1
иС
2
изобщего
решения у(х, С
1
, С
2
) уравненияЭйлера.
0
'
=−
yy
F
dx
d
F
0
)(
'
=
∂
∂
−
=ax
y
ay
f
F
0
)(
'
=
∂
∂
−
=bx
y
by
f
F
Задачи на условный экстремум.
Задачивариационногоисчисления, вкоторыхнаискомыефункциинакладываются,
помимограничныхусловий, дополнительныеограничения, называютсязадачамина
условныйэкстремум.
Рассмотримследующуюзадачуобэкстремумефункционала, зависящегоот
несколькихфункций,
(42)
сграничнымиусловиями
, , , (43)
при дополнительных ограничениях, заданных уравнениями с граничными
условиями
∫
′′
=
b
a
nnn
dxxyxyxyxyxFxyxyJ ))(),...,(),(),...,(,()](),...,([
111
)0(
)(
kk
yay
=
)1(
)(
kk
yby
=
n
k
,...,
1
=
0),...,,,...,,(
11
=
′
′
nni
yyyyx
ϕ

Этазадачавариационногоисчисленияназывается задачейЛагранжа.
Введём функциюЛагранжа рассматриваемойзадачи
,(45)
где – произвольныефункции (множителиЛагранжа).
ПрирешениизадачиЛагранжаиспользуетсяследующеенеобходимоеусловие
экстремумафункционала (42).
Необходимоеусловие 6.
Еслифункции у
1
(х),..., y
n
(x) доставляютслабыйэкстремумфункционалу (42) при
условиях (44), тосуществуютмножителиЛагранжа
, i=1,…, m, m<n,
прикоторыхэтифункцииудовлетворяютсистемеуравненийЭйлера
, i=1,…, n , (46)
записанныхдляфункционала
+
′
′
=
′
′
),...,,,...,,(),...,,,...,,...,,(
11111 nnmnn
yyyyxFyyyyxL
λ
λ
∑
=
′′
m
i
nnii
yyyyxx
1
11
),...,,...,,()( ϕλ
];[)(
1
baCx
i
∈
λ
)(x
i
λ
0=−
′
kk
yy
L
dx
d
L
∫
=
b
a
n
LdxyyI .),...,(
1
)(x
i
λ
Задачанаусловныйэкстремумфункционала (42) сграничнымиусловиями (43)
придополнительныхусловиях
,i=1,…, m, m<n. (47)
(интегральныесвязи) называется изопериметрическойзадачей.
ФункцияЛагранжаданнойзадачиимеетвид
,(48)
гдемножителямиЛагранжа , i=1,...,m,являютсяпроизвольные вещественные
числа.
Прирешенииизопериметрическойзадачииспользуетсяследующеенеобходимое
условиеэкстремума, подобноеусловию, сформулированномувнеобходимомусловии 6
длязадачиЛагранжа.
Необходимоеусловие 7.
Еслифункции y
1
(x),.., у
n
(х) доставляютслабыйэкстремумфункционалу (42) при
условиях (43),(47), тосуществуютчисла (множителиЛагранжа), прикоторых
этифункцииудовлетворяютсистемеуравненийЭйлера
,
k
=
1
,
…
,
n
,
(
49
)
i
b
a
nni
CdxyyyyxF =
′′
∫
),...,,,...,,(
11
+
′′
=
′′
),...,,...,(),...,,,...,,...,,(
11111 nnmnn
yyyyxFdxyyyyxL λλ
∑
=
′′
m
i
nnii
yyyyxF
1
11
),...,,,...,,(λ
m
λ
λ
,...,
1
0=−
′
kk
yy
L
dx
d
L
L
i
λ
i
λ

Вторая вариация и достаточные условия экстремума
Вспоминаяоглубокойаналогиимеждудифференциальнымивариационным
исчислениями, естественноожидать, чтоприпереходекдостаточнымусловиям
экстремумафункционаловбудетвведенопонятие, играющеевэтомвопросетужероль,
чтодифференциалвторогопорядкаприисследованииэкстремумафункций. Этим
понятиемявляетсявтораявариация.
Вариации высших порядков
Заменаприращенияфункционаланаеговариацию, какизаменаприращения
функциинаеедифференциал, можетбытьуточненаспомощьюдобавлениячленов
высшегопорядкамалости. Этоприводиткразложениювряд
(1)
совершенноаналогичныйрядуТейлорадляфункций. Здесь δ
2
I, δ
3
I,…-вариации
соответственновторого, третьегоит.д.порядков (коротко - вторая, третьяит.д.
вариации) функционала I. Каждаяизнихполучаетсяспомощьюварьирования
предыдущей (т.е. ит.д.), впроцессекоторого δy считаетсянезависящимот у,
т.е. неварьируется.
Каждаяизэтихвариацийобладаетотносительно δy свойствомоднородностис
соответствующимпоказателем:
, С=const.
Этоозначает, чточленывправойчасти (1) имеютпоследовательнопервый, второй,
третийит.д.порядкималостиотносительно δy (точнееговоря, относительно || δy ||,
...};{
!
3
1
};{
!
2
1
};{}{}{
32
+++=−+ yyIyyIyyIyIyyI δδδδδδδ
)(
2
II
δ
δ
δ
=
};{};{ yyCyCyI
nnn
δ
δ
δ
δ
=

Ранеемыпользовалисьтолькопервымчленомряда (1). Вэтомразделемыбудем
пользоватьсятакжеивторымчленом, т.е. болееточнойформулой
(2)
Вконкретныхпримерахразложение (1), апотомуи(2) получаютсяспомощью
обычногорядаТейлора. Например, дляфункционала
Получаем
,
гдевF, ит.д.должныбытьподставленызначения х, у, у'. Отсюдаполучаемдля
второйвариациивыражение
).||(||};{
!
2
1
};{}{};{
32
yOyyIyyIyIyyI δδδδδδ ++=−
{} ( )
dxyyxFyI
b
a
∫
′
= ,,
∫ ∫
+
′′
+
′
+=
′
+
′
+=∆+
′
b
a
b
a
yy
yFyFFdxyyyyxFyyI )([),,(}{ δδδδ
dxyFyyFyF
yyyyyy
...])2(
!
2
1
22
+
′′′
+
′′′
+
′′
+
′′′
δδδδ
y
F
′
∫
+
′′′
+
′′
=
′
b
a
yyyyyy
dxyFyyFyFyyI )'"2(};{
2
''
22
δδδδδδ
2222
)'(',)( yyyy
δ
δ
δ
δ
=
=

Условия экстремума в терминах второй вариации
Пустьфункционал I{у} принимаетдля стационарноезначение, т. е. .
Другимисловами, пустьвыполненоосновноенеобходимоеусловиедляэкстремума. Тогда
при вправойчасти (2) первыйчленотсутствует, ипотомуглавнымстановитсявторой.
Поэтомуприрассмотренииэкстремумафункциинесколькихпеременныхприходимк
следующимвыводам:
если δ
2
I >0 длялюбой δу (конечно, кромевариации δу≡0, когда δ
2
I =0), топри .
функционал I{у} имеетминимум;
если δ
2
I <0длялюбой δу, топри функционал I{у} имеетмаксимум;
если δ
2
I можетприниматьзначенияобоихзнаков, топри функционал I{y} имеет
минимаксиэкстремуманебудет.
Единственныйслучай, когдапо δ
2
I нельзясудитьоналичииэкстремума, тот, когда δ
2
I
знакаменятьнеможет, номожетобращатьсявнуль (вчастности, еслионатождественнопо
δу равнанулю). Мынебудемздесьразбиратьэтотслучай.
Болеетщательныйанализпоказывает, чтодостаточноеусловиеминимумавобщем
случаеимеетвид
(C=const>0).
Этоусловиедляфункциональныхпространствболеесильное, чемпросто δ
2
I >0. Однако
дляобычныхзадачвариационногоисчисленияэтоуточнениенесущественно.
Приведенныеформулировки, какиизученноеранеенеобходимоеусловие, желательно
преобразоватькравносильномувидутребования, наложенногонепосредственнонаискомую
функцию
у
(
х
)
.
Это
преобразование
проводится
различно
для
разных
классов
функционалов
.
0};{ ≡yyI δδ
yy =
22
||||};{ yCyyI δδδ ≥
yy =
yy =
yy =
yy =
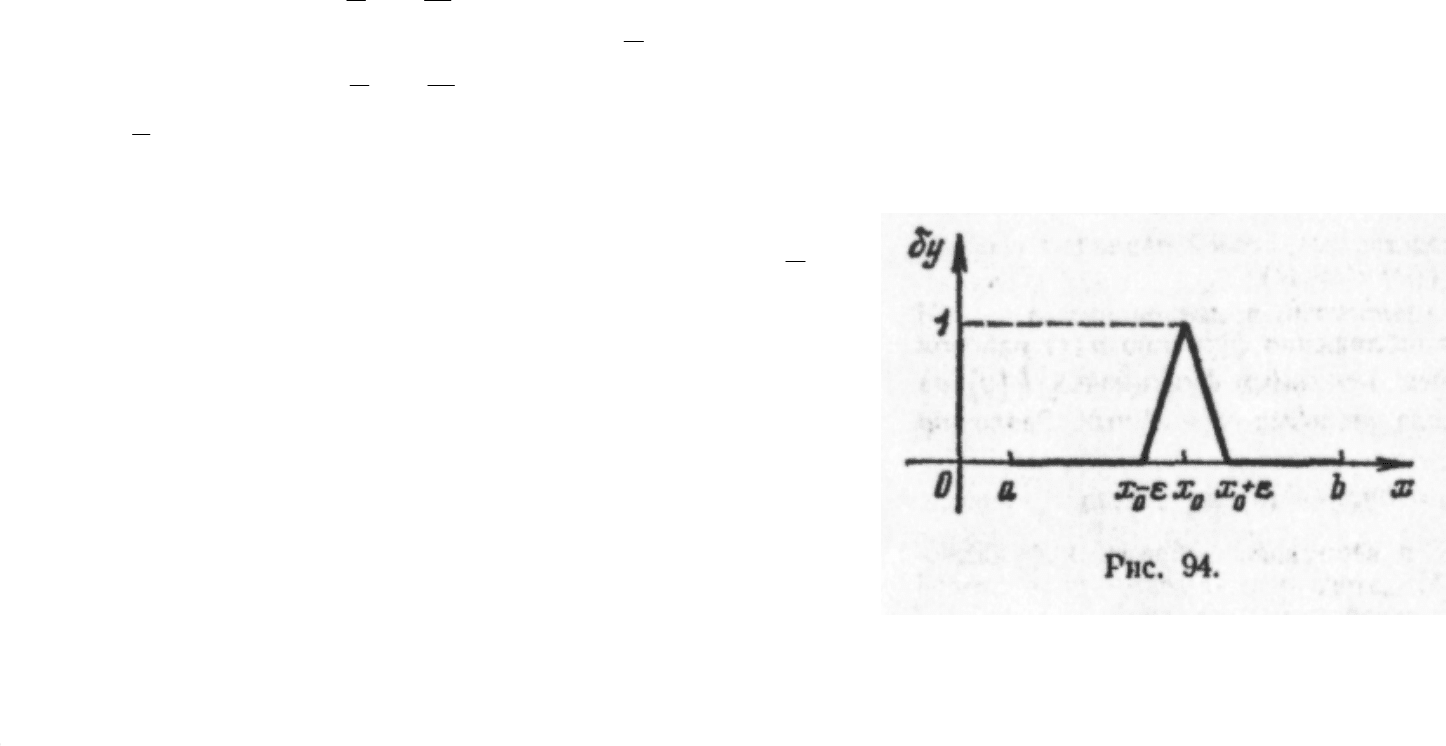
В самом деле, обозначим для краткости
коэффициентыквадратичнойформыподзнаком
интеграла (3), послеподстановкивних ,
соответственно через φ(x), ψ(x), χ(x), ипусть
χ(x
0
)>0(a<x
0
<b)(мысчитаемвсерассматриваемые
функциииихпроизводныенепрерывными, такчто
если χ(x
0
)≤0 при а<х<b, тоэтоверноипри a≤x≤b).
Выберемвкачестве δу функцию, графиккоторой
изображенжирнойлиниейнарисунке.(Приэтом,
еслижелатьиметьделотолькосфункциямииз С
1
,
тоуголкиможнокакугодномалоскруглить.)
Необходимые условия Лежандра
Рассмотримфункционал
при некоторых граничных условиях. Вторая вариация такого функционала
выражаетсяпоформуле (3), т.е.
Легко проверить, что:
если допускаетпри a ≤ x ≤ b (необязательнодлявсехтаких х)
положительныезначения, тои допускаетположительныезначения;
если допускаетпри a ≤ x ≤ b отрицательныезначения, тои.
допускаетотрицательныезначения.
{} ( )
dxyyxFyI
b
a
∫
′
= ,,
∫
+
′′′
+
′′
=
′
b
a
yyyyyy
dxyFyyFyFyyI )'"2(};{
2
''
22
δδδδδδ
};{
2
yyI δδ
))(),(,("
''
xyxyxF
yy
′
)(xyy =
))(),(,("
''
xyxyxF
yy
′
};{
2
yyI δδ
Тогда
. (5)
Заменяяпрималом ε коэффициентыихзначениямивточкех
0
,получаем
приближенныевыражениядляслагаемыхвправойчасти (5)
, ψ(x
0
)∙0, .
Значит, прималом ε всясумма (5) положительна, чтоитребовалосьдоказать.
Сравниваяполученныйрезультатсусловиямиэкстремума, приведеннымивыше,
приходимкнеобходимымусловиямЛежандра:
еслифункционалпринекоторыхграничныхусловияхимеетпри (хотябы
слабый) минимум, то
,(a≤x≤b)
еслижемаксимум, то
∫∫∫
+
−
+
−
+
−
++=
ε
ε
ε
ε
ε
ε
δχδδψδϕδδ
0
0
0
0
0
0
222
')(')(2)(};{
x
x
x
x
x
x
dxyxdxyyxdxyxyyI
εϕ
3
2
)(
0
⋅x
ε
χ
2
)(
0
⋅x
yy =
0))(),(,("
''
≥
′
xyxyxF
yy
0))(),(,("
''
≤
′
xyxyxF
yy
)(xy
))(),(,("
''
xyxyxF
yy
′
yy =
Аналогичнорассматриваютсяфункционалыотнесколькихфункций, напримерот
двухфункций. Здесьразложения (1) и (2) такжеимеютместо, но у и δу ужеявляются
векторнымифункциями. Втораявариация, взамен (3), приобретаетвид
,
гдеиндексы i, j принимаютнезависимоодинотдругогозначения 1,2(авслучае n
искомыхфункций - все n значений).
Рассуждая, каквыше, приходимкнеобходимымусловиямЛежандраивэтом
случае:
еслифункция доставляетрассматриваемомуфункционалупринекоторых
граничныхусловияхминимум, токвадратичнаяформа
(6)
прилюбом х (а≤x≤b) недолжнаприниматьотрицательныезначения, т. е. должна
бытьнеотрицательной (всесобственныезначенияеематрицыдолжныбыть≥0);
еслидля будетмаксимум, тоформа (6) должнабытьвсюдунаотрезке а≤х≤b
неположительной,
∫
∑∑∑
++=
b
a
ji
jiyy
ji
jiyy
ji
jiyy
dxyyFyyFyyFyyI
jijiji
)''"'""(};{
,
''
,
'
,
2
δδδδδ
∑
′′′
′′
n
ji
jiyy
xyxyxF
ji
,
))(),(,( ξξ
)(xy
ji
yy
F
′
′
)(xyy =
)(xyy =
)(xyy =
Необходимое условие Якоби
Пустьдлянекоторойфункции удовлетворяютсяуравнениеЭйлераиграничные
условия, т.е. онапридаетфункционалупритакихусловияхстационарноезначение.
Обозначимдлякратности ит.д. Тогда, преждевсего, всилу
условийЛагранжа, если меняетзнакнаинтервале а≤х≤b,тозначение .
минимаксное. Наличие нулей у всегда вызывает существенныеосложнения.
Поэтомумыбудемпредполагать, что сохраняетзнак, дляопределённости . (a≤
x ≤b).
Обозначимнаминуту δу=z вфункционале (3), кудаподставлено ; тогда
уравнениемЭйлерадлянегобудет
. (7)
Ононазывается уравнениемЯкоби дляисходногофункционала. Обозначимчерез
а* точку, сопряжённуюсаотносительноэтогоуравнения. Тогда, еслиа*>b, то
функционал (3) имеетпри δу=0 минимум, апотому функционал I{y} имеетпри .
слабыйминимум; еслижеа*<b, тофункционал I{y} имеет при слабый
минимакс. Ясно, чтоесли (a≤ x ≤b), товместоминимуманадоговоритьо
максимуме. Этиусловияэкстремума, выраженныевтерминахсопряжённыхточек,
называются условиямиЯкоби.
)(xy
))(),(,( xyxyxFF
yyyy
′′′
=
′′
}{yI
yy
F
′′
′′
0>
′′
′′
yy
F
)(xyy =
0)()( =
′′
−
′′
+
′′′′
′′′
zFF
dx
d
zF
yyyyyy
)(xyy =
0<
′′
′′
yy
F
yy
F
′′
′′
yy
F
′′
′′
)(xyy =
