Презентация - Семенкин Е.С. Методы оптимизации
Подождите немного. Документ загружается.


Можносказатьчтофункционал – этофункция, укоторойзначенияминезависимой
переменной y(x) служатобычныефункции, азначениямизависимойпеременной I
служатчисла.
Формула
определяетдругойфункционал, причем линейный, т.е.
J{C⋅y}=C⋅J{y}(C=const), . (5)
{} ( )
dxyxyyJ
∫
′
+=
2
0
}
{
}
{
}
{
2121
y
J
y
J
y
y
J
+
=
+
Формула
определяетещеодинфункционал, отличныйот (4), таккак K{y} заданнадругом
классефункций y(x), именно, определенныхпри 1≤ x ≤3. Втожевремяфункционал
{}
∫
=
2
0
2
dxzzL
{
}
{
}
yLyI
≡
∫
=
3
1
2
}{ dxyyK

Функциональные пространства
Прирассмотрениифункционаловиихэкстремумовбываетполезноуточнить
область определения функционала, т.е. совокупность функций, для которых он
рассматривается. Обычноэтасовокупностьпредставляетсобойнекотороелинейное
пространство – илиегочасть,–состоящееизфункций, надкоторымилинейные
действиявыполняютсяпопростейшимправилам. Такиепространстваназываются
функциональнымипространствами, оничащевсегобесконечномерные.
Функциональныепространстваобычноявляются нормированными, т.е. вних
имеетсяпонятие нормы, характеризующейуклонениефункцииоттождественногонуля.
Нормафункции f обозначаетсячерез || f ||, онапредставляетсобойконечное
действительноечислоидолжнаудовлетворятьследующимтребованиям (аксиомы
нормы):
1.|| f ||≥0, причем || f ||=0 толькодлятождественнонулевойфункции f.
2.|| af||=| a|·||f|| (a=const).
3.|| f +g||≤|| f ||+|| g||.
Понятиеуклоненияфункцийможетбытьвведенопо-разному. Соответственно
этому, рассматривают различные функциональные пространства, состоящие из
функций, заданныхнакаком-либоинтервале a ≤ x ≤ b.(Отметим, чтовсефункции,
составляющиелинейноефункциональноепространство, должныбытьзаданынаодном
и
том
же
интервале,
так
как
в
противном
случае
их
нельзя
было
бы
складывать
друг
с

Этипространстваподробноизучаютсявкурсефункциональногоанализа; наиболее
употребительны следующие пространства. (Считаем все участвующие величины
вещественными, авсеобластиопределенияфункцийконечными.)
1. Пространство C[a,b]функций, заданныхинепрерывныхнаконечном
интервале a ≤ x ≤ b, снормой
Этанормаотвечаетравномерномууклонениюфункцийдруготдруга.
2. ПространствоС
1
[a,b]функций, заданныхинепрерывныхпри a ≤ x ≤ b вместе
сосвоейпроизводной, снормой
(6)
(ВкачественормывС
1
можновзятьтакженесумму, анаибольшееизслагаемых,
стоящихвправойчасти; эторазличиеоказываетсянесущественным.)
Аналогичновводятся пространстваС
n
[a,b]при n=2,3,....
3. ПространствоГильберта L
2
[a,b]функций, заданныхпри a ≤ x ≤ b ине
обязательнонепрерывных, длякоторыхнорма
|| f ||=
(7)
|)(|
max
xff
bxa ≤≤
=
.|)('|max|)(|max xfxff
bxabxa ≤≤≤≤
+
=
∫
a
b
dxxf
2
)]([
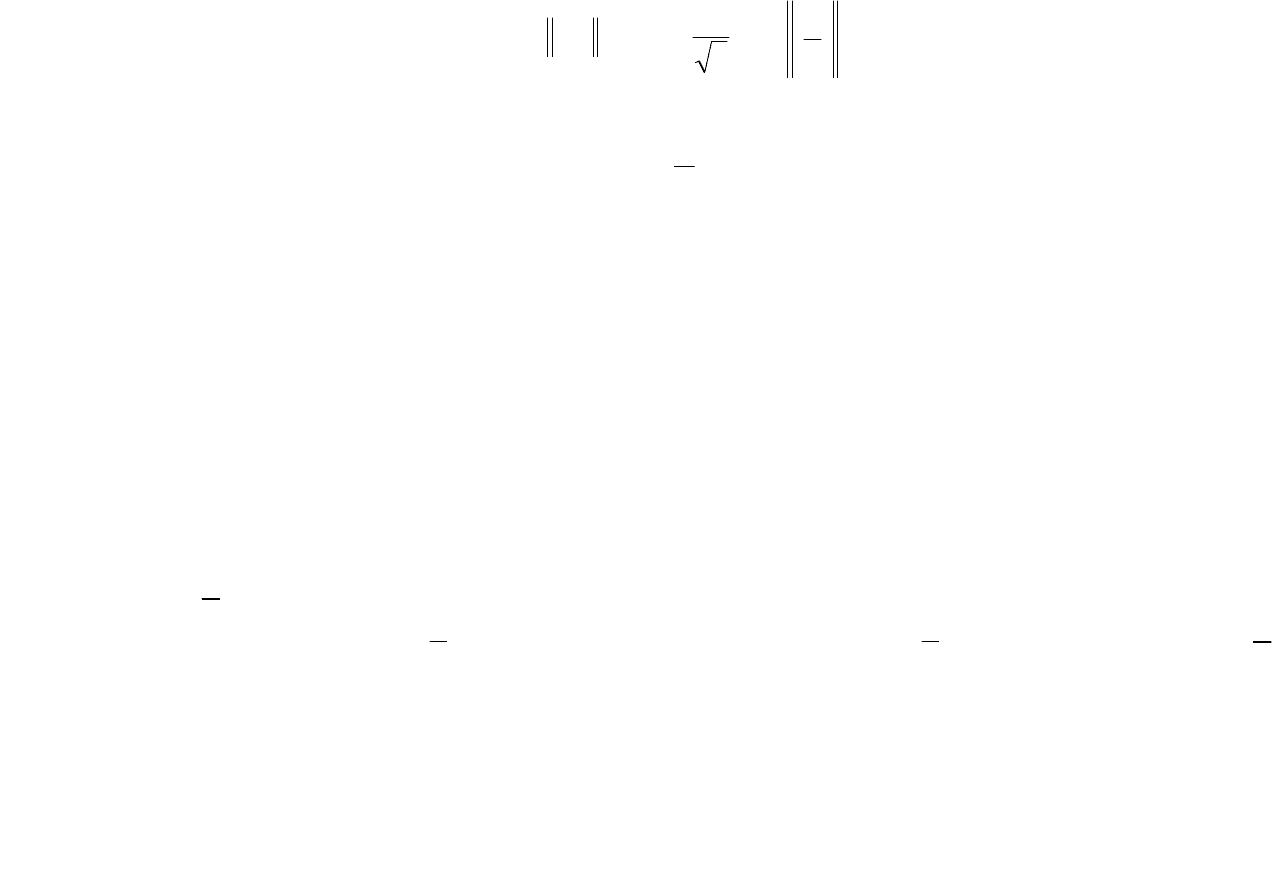
Еслиизтекстанеясно, какаяименнонормаимеетсяввиду, тонадописатьболее
подробно:|| f ||
C[a,b]
ит.п.Подчеркнем, чтовнормированномпространственорма
каждогоэлементаконечна. Например,
, ;
поэтому, функция y=x
2
входитвпространство L
2
[0,1](являетсяегоэлементом,
обобщеннымвектором), афункция невходит.
Внормированномпространствевводитсяпонятиерасстояния p междулюбыми
элементами f,gпоформуле
p(f, g)=|| f – g ||;
дляфункциональныхпространствтакоерасстояниеестькакразуклонение
функций f и g друготдруга.
Отчетливое представление о функциональных пространствах полезно при
рассмотренииэкстремумовфункционалов. Всамомделе, пустьфункционал I{y} имеет
при
локальный
максимум
.
Это
значит,
что
для
всех
функций
y
(
x
),
не
5
1
]1,0[
2
2
=
L
x
∞=
]1,0[
2
1
L
x
x
y
1
=
(
)
xyy =
(
)
xy
}{}{ yIyI <
(
)
xy
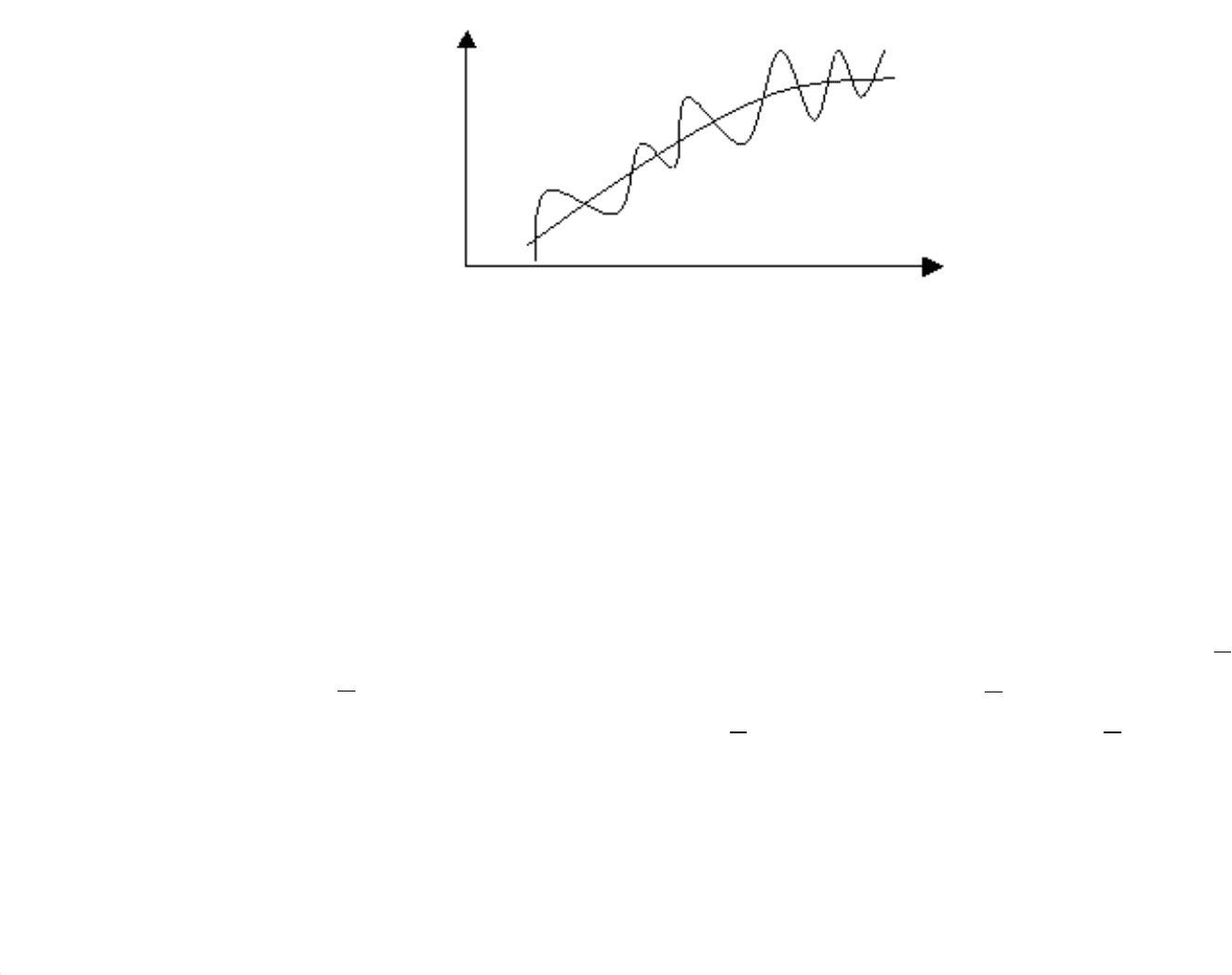
Например, можнолисчитатьдвефункциинарисункеблизкими? Таккак
существуютразличныевидыуклоненийфункций, тоответнаэтотвопросзависитот
того, какойвидуклонения, т.е. какоефункциональноепространство, принятьзаоснову.
Таконимогутбытьблизкими, еслиихрассматриватьвC[a,b], нодалекимивC
1
[a,b].
Соответственно этому рассматриваются различные типы экстремумов
функционалов. Вдальнейшеммыбудемисследовать, какправило, функционалы,
которыеестественнорассматриватьлибовС
1
,либовС.Тогда, если для
всех y, близкихк всмысле C, тоговорят, чтонафункции достигается сильный
максимум функционала I{y}; еслиже длявсех y, близкихк всмысле C
1
,
тоговорятослабоммаксимуме. Приэтомсильныйэкстремумвсегдабудеттакжеи
слабым, нообратноенеобязательно.
}{}{ yIyI <
y
y
}{}{ yIyI < y
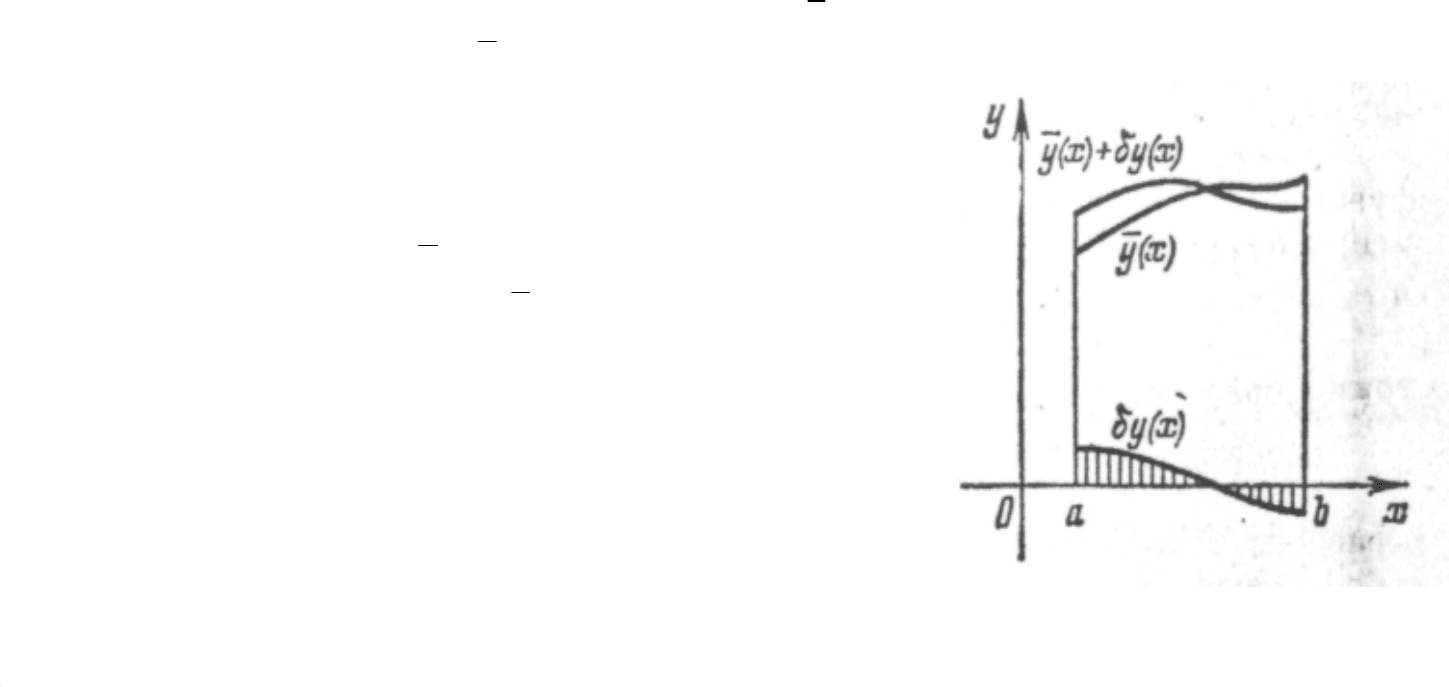
Вариация функционала
Вариацияодноизцентральныхпонятийприизучениинелинейныхфункционалов,
оноиграеттужероль, чтопонятиедифференциалаприизучениинелинейныхфункций.
Дифференциалнелинейнойфункцииравенглавнойлинейнойчастиееприращения,
заменаприращениянадифференциалозначаетлинеаризациюфункциипрималом
измененииаргумента;
Вариациянелинейногофункционаларавнаглавнойлинейнойчастиегоприращения,
заменаприращениянавариациюозначаетлинеаризациюфункционалаприпереходеот
однойфункции (откоторойзависитзначениефункционала) кдругой, близкойфункции.
Рассмотрим, например, функционал (4). Пустьфункция y(x), откоторойзависитего
значение, сначаласовпадаласнекоторой , азатеммыперешликнекоторойдругой,
близкойфункции .
(
)
xy
(
)
(
)
xyxy δ+
Здесь - это вариация
функции у(х), т.е. произвольная функция,
мало уклоняющаяся от нуля и добавляемая к
исходной функции для получения новой,
проварьированной функции (см. рисунок).
(Приэтоммалоеуклонениеотнуляпонимаетсяв
смыслетойнормы, котораяпринятазаоснову,
например, нарисункемалостьпонимаетсявсмысле
С
1
).
(
)
xy
δ
(
)
xy
(
)
(
)
xyxy δ+

Припереходеот к функционал (4) получитприращение
∆I .(10)
Пустьтеперьфункция зафиксирована, афункцию можновыбирать
произвольно. Мывидим, чтотогда∆Iсостоитиздвухчастей, каждаяизкоторых
представляетсобойфункционалотносительно . Перваячасть
(11)
обладаетсвойствомлинейностипо δу, т.е. этолинейныйфункционал, тогдакак
втораячасть
прималых δу имеетвысшийпорядокмалости. Такимобразом,(11) представляет
собойглавную (т. е. сточностьюдочленавысшегопорядкамалости) линейнуючасть
приращения (10) функционала (4) припереходеот к . Выражение (11)
иназывается (первой) вариациейδIфункционала; можнонаписать
(
)
xy
(
)
(
)
xyxy δ+
{ } {}
[ ]
() () ()
[ ]
∫∫∫∫
+⋅=−+=−+=
2
0
2
2
0
2
2
0
2
0
2
2 dxxydxxyxydxydxyyyIyyI δδδδ
(
)
xy
(
)
xy
δ
yyy −=δ
() ()
dxxyxy δ⋅
∫
2
0
2
()
[ ]
∫
2
0
2
dxxyδ
(
)
(
)
xyxy δ+
() ()
dxxyxydxyI
∫ ∫
⋅==
2
0
2
0
2
2 δδδ
(
)
xy
(
)
xy

Разобранныйпримерявляетсятипичным. Еслизаданпроизвольныйфункционал
I{у} имыпереходимотфункции у(х) кфункции у(х)+ δу(х), то, какправило,
приращениефункционала
можнопредставитьввидесуммыдвухслагаемых
(12)
первоеизкоторыхпрификсированнойфункции у(х) представляетсобойлинейный
функционалотносительно δу(x), автороеимеетотносительно δу(x) высшийпорядок
малости. Тогдапервоеслагаемое, вправойчасти (12) иназывается вариацией
функционала I, т. е.
Вслучаях, когдаслагаемымвысшегопорядкамалостиможнопренебречь, можно
сказатьпросто, чтовариацияфункционала – этоегобесконечномалоеизменение, т.е.
изменение, полученноезасчетбесконечномалойвариациифункции, откоторой
зависитэтотфункционал. Заменаприращенияфункционаланаеговариациюозначает
линеаризацию этого функционала, аналогично рассуждениям, приводимым при
введении
понятия
дифференциала
функции
.
}
{
}
{
y
I
y
y
I
I
−
+
=
∆
δ
},
;
{
}
;
{
11
y
y
R
y
y
I
I
δ
δ
+
=
∆
};{
1
yyII δδ =

Пусть, например, рассматриваетсяфункционалвида
, (13)
гдевпроцессеинтегрирования y считаетсязависящимот х, у=у(х). Тогда
. (14)
Но, таккак {членывысшегопорядкамалости},
то, подставляяв(14) иотбрасываяэтичлены, получим
(15)
Дляфункционала
(16)
аналогично получаем
∫
=
b
a
dxyxFyI ),(}{
∫
−+=∆
b
a
dxyxFyyxFI )],(),([ δ
(
)
(
)
(
)
+
′
+=+ yyxFyxFyyxF
y
δδ ,,,
( ) ( )
ydxyxFdxyxFI
b
a
y
b
a
δδδ
∫∫
′
== ,,
{} ( )
dxyyxFyI
b
a
∫
′
= ,,
( ) ( )
[ ]
dxyyyxFyyyxFI
b
a
yy
∫
′′′
+
′′
=
′
δδδ ,,,,
y
′
δ
(
)
y
′
δ
( )
′
yδ

Необходимое условие экстремума
Это условие совершенно аналогично необходимому условию экстремума
функцииоднойилинесколькихпеременных. Допустим, чтонекотораяфункция .
реализуетлокальныймаксимумилиминимумфункционала I{у} ввыбранном
функциональномпространстве (R), причемэтотфункционалимеетвариацию ,
т. е. допускаетвблизи линеаризацию. Крометого, будемсчитать, что
рассматривается внутренний (не граничный) экстремум, т.е. функционал I{у}
определендля всеху,достаточноблизкихк всмыслевыбраннойнормы; этобудет
предполагатьсявсюдудалее, еслинеоговоренопротивоположное.
Тогдадлялюбой должнобыть
. (18)
Всамомделе, пустьдляопределенностипри функционал I имеет
минимуми >0 длянекоторой . Подставимв(12) kδy вместо δу, где k -
скаляр: получим
Однако
при
малых
|
k|
левая
часть
должна
быть
положительной,
а
правая
имеет
(
)
xy
};{ yyI δδ
(
)
xyy =
y
(
)
Ry
∈
δ
0};{ =yyI δδ
(
)
xyy =
};{ yyI δδ
y
δ
});{
1
};{(};{};{}{}{
_
1
_
1
_
1
_
1
__
ykyR
k
yyIkykyRykyIyIykyII δδδδδ +=+=−+=∆
