Презентация - Семенкин Е.С. Методы оптимизации
Подождите немного. Документ загружается.


ТеоремаВейерштрасса. Пустьдопустимоемножество X являетсякомпактным
(т.е. ограниченнымизамкнутым) инепустым. Тогданепрерывнаяцелеваяфункция
f(x), определенная на этом множестве, достигает глобального максимума на
внутреннейилиграничнойточкемножества X.
Доказательствоэтогоутвержденияследуетизтогофакта, чтообразнепрерывной
функции, определеннойнакомпактноммножестве, тожеявляетсякомпактным. Тогда
мыимееммножестводействительныхчисел F(X), удовлетворяющихусловию
F(X) = {z∈E z = F(x) для x∈X},
котороеявляетсякомпактным. Всякоекомпактноемножестводействительных
чиселимеетверхнююгрань. Такимобразом, если F* являетсяверхнейгранью F(X), то
существует x*∈X, удовлетворяющийусловию F(x*)=F*, атаккак F(X) ≤ F(x*) для
всех x∈X, тоточка x* являетсяглобальныммаксимумом.
Обобщая эту теорему на случай бесконечномерного пространства, можно
получитьосновнуютеоремусуществованиядлязадачуправления – обобщенную
теоремуВейерштрасса.
ОбобщеннаятеоремаВейерштрасса. Решениеобщейзадачиуправления (9)
существует, еслицелевойфункционал J{u(t)} являетсянепрерывнымфункционаломот
функцийуправленияиподмножество U бесконечномерногопространства, ккоторому
принадлежатуправления, являетсякомпактным.
Длядоказательстватеоремыобозначимсимволом J* точнуюверхнююграницу
функционала J{u(t)} повсем {u(t)}∈U, т.е.J{u(t)} ≤ J* привсех {u(t)}∈U. Возьмем
некоторуюпоследовательностьуправлений {u
p
}, такуючто
J*- <J{u
p
} ≤ J*.
Так как множество U компактное, то эта последовательность содержит
подпоследовательность {u }, сходящуюсякнекоторомууправлению {u*}∈U. Тогда
J*- <J{u } ≤ J*
иследовательно,
J{u }=J*.
Нотаккакфункционал J непрерывен, т.е.
J{u }=J{u*},
p
1
k
p
k
p
1
∞→
k
p
lim
k
p
k
p
∞→
k
p
lim
k
p
Источник: Интриллигатор М. Математические методы оптимизации и экономическая
теория. – М.: Айрис-пресс, 2002. –576 с.

Задача управления в классическом вариационном исчислении состоит в
следующем: средимножествафункцийвремени – фазовыхтраекторий,-соединяющих
двефиксированныеточки, соответствующиеначальномуиконечномумоментам
времени, требуется выбрать функцию, максимизирующую (минимизирующую)
некоторыйинтегралотзаданнойфункции, котораязависитотфазовойкоординаты,
скоростиизмененияфазовойкоординатыивремени. Такимобразом, классическая
задачавариационногоисчисления имеетвид
= , x(t
0
)=x
0
, x(t
1
)=x
1
,
где J(x, x', t)–фиксированнаянепрерывнодифференцируемаяфункция, а t
0
, t
1
, x
0
, x
1
– фиксированныепараметры.
Эта задача является частным случаем общей задачи управления:
J
tx )}({
max
∫
1
0
)),('),((
t
t
dtttxtxI
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
найти
= + F(x
1
, t
1
)
приусловии, что x' = f(x(t), u(t), t), t
0
и x(t
0
)=x
0
фиксированы,
(x(t), t)∈T при t = t
1
,{u(t)}∈U.
Jmax
t })({u
∫
1
0
) ),( ),((
t
t
dttttI ux
вкоторуюневходитфункцияконечныхпараметров (задачаЛагранжа), входитодна
фазоваякоординатаиодинуправляющийпараметр – скоростьизмененияфазовой
координаты.

Уравнениедвижениявэтомслучаеимеетвид
x' = u,
так, что x' в I(⋅⋅⋅) заменяет u, ауправляющийпараметрможетприниматьлюбое
значение, т.е.
U = E.
Следовательно, управлениедолжноотвечатьединственномуусловию – быть
кусочно-непрерывной функцией времени. Любая траектория {x(t)} называется
допустимой, еслионаудовлетворяетграничнымусловиямиз (1) иследующему
условиюнепрерывности: x(t)–непрерывная, а x'(t)–кусочно-непрерывнаяфункция
времени.
Классическую задачу вариационного исчисления можно рассматривать как
динамический аналог классической задачи математического программирования.
Вариационноеисчислениенепосредственнопримыкаетктеорииэкстремумовфункций
вещественныхпеременных.
ВариационноеисчислениеосновановXVIII векеЛ.ЭйлеромиЖ.Лагранжем,
значительноразвитовXIX векевтрудахрядаматематиковивнастоящеевремя
превратилосьводинизважнейшихразделовтеоретическойиприкладнойматематики,
Примеры простейших задач вариационного исчисления
Историческипервойзадачей, известнойвглубокойдревностииотнесенной
впоследствиикзадачамвариационногоисчисления, явиласьтакназываемая задача
Дидо. Легендаговорит, чтоДидо – царицаодногоизгосударствДревнейГреции,
преследуемаяцаремсоседнегогосударства, бежалавСевернуюАфрикуипопросилау
местногонаселенияучастокземли, которыйможноохватитьшкуройвола. Получив
согласиенастольничтожнуюпросьбу, онанаглазахуизумленныхзрителейразрезала
шкурунатонкие ремешкии,связавихдругсдругом, охватилаполученнойнитью
изрядныхпотемвременамучасток; развернувнанемстроительство, онаосновалана
этомучасткезнаменитыйвдревностигородКарфаген.
Ужеантичныеученыезаинтересовалисьматематическойсторонойэтойлегенды:
допустим, чтонитьужесвязана; кактогданадорасположитьее, чтобыохваченныйею
участокимелнаибольшуюплощадь?
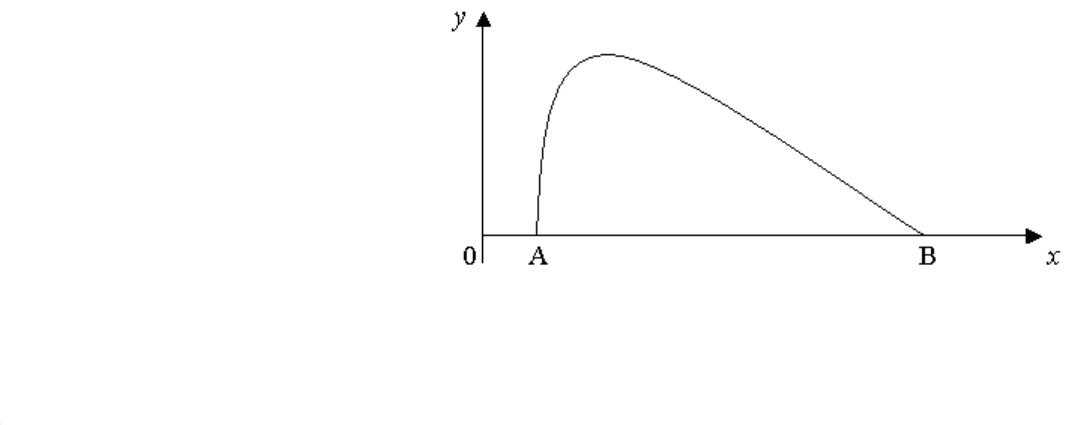
Пусть концы нити расположены в заданных точках А(a,0) и В(b,0) на берегу моря.
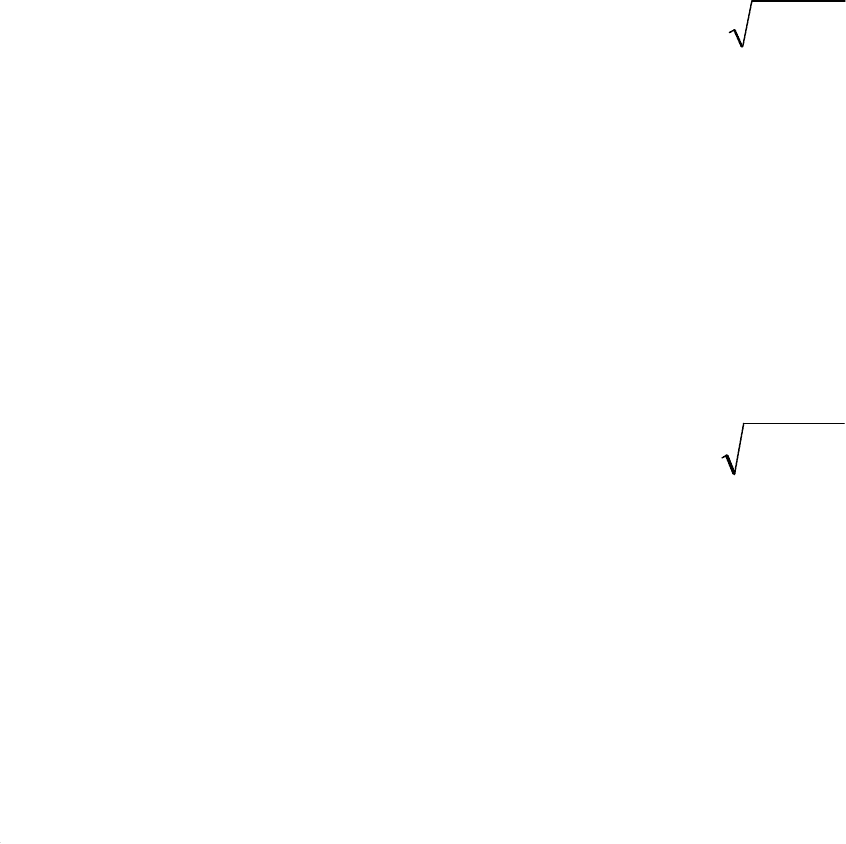
Еслитогдавыбратьосикоординаткакнарисунке, тозадачасводитсяк
максимизацииплощади, т.е. интеграла
S=
(y=y(x)–уравнениесухопутнойграницыучастка), призаданномзначениидлины
нити, т.е. интеграла
L= ,
изаданныхкраевыхзначениях
y(a)=0, y(b)=0.
Ужевдревностибылообнаружено, чтоискомойформойнитислужитдуга
окружности.
∫
b
a
dxxy )(
∫
+
b
a
dxy
2
'1
Задачаократчайшемрасстоянии
Наплоскости xOy даныдветочкиА
1
(x
1
,y
1
)иА
2
(x
2
,y
2
). Расстояниемеждуэтими
точкамиопределяетсяпоформуледлиныдуги:
(1)
Этовыражениеявляетсяфункционалом, потомучточисленнаявеличинаего
зависитотвидаилиформыкривых, проходящихчерезточкиА
1
иА
2
.Черезэтиже
точкиможнопровестибесчисленноемножествокривых. Изэтогомножестванужно
найтиэкстремаль, т.е. такуюкривую, прикоторойинтеграл (1) имеетминимум. Такой
кривой
будет
прямая
линия
–
это
совпадает
с
определением
Евклида,
который
dxyS
x
x
∫
′
+=
2
1
2
1

Задачаокатеноиде
ЧерездвезаданныеточкиА
1
(x
1
,y
1
)иА
2
(x
2
,y
2
)вверхнейполуплоскостипроходит
некотораякривая, непересекающаяось x. Этакриваявращаетсявокругоси x.
Боковаяповерхностьтелавращенияопределяетсяпоформуле:
(2)
Выражение (2) являетсяфункционалом, потомучточисленнаявеличинаего
зависитотвидаилиформыкривой, проходящейчерезточкиА
1
иА
2
.Извсевозможных
кривых, соединяющихэтиточки, нужновыбратьэкстремаль, т.е. такую кривую, при
которойинтеграл (2) будетиметьминимум. Приэтом y(x
1
)=y
1
, y(x
2
)=y
2
. Такойкривой
окажетсяцепнаялиния, откудаисамоназваниезадачи.
′
+=
∫
2
1
2
12
x
x
dxyyP π
Задачаобрахистохроне.
Тяжелаяматериальнаяточка M смассой m скатываетсяподдействиемсилы
тяжестиизположенияА
1
(x
1
,y
1
)вположениеА
2
(x
2
,y
2
)поидеальногладкойкривой.
Возьмемкакую-либопромежуточнуюточкуВ(x,y). Пустьскоростьдвиженияв
точкеА
1
будет v
1
, авточкеВ–v.Тогдапозаконусохраненияэнергии
,
где g – ускорение свободного падения, а h = y
1
–y. Для упрощения примем v
1
=0, т.е.
начальная скорость равна 0.
mgh
mvmv
=−
2
2
2
1
2
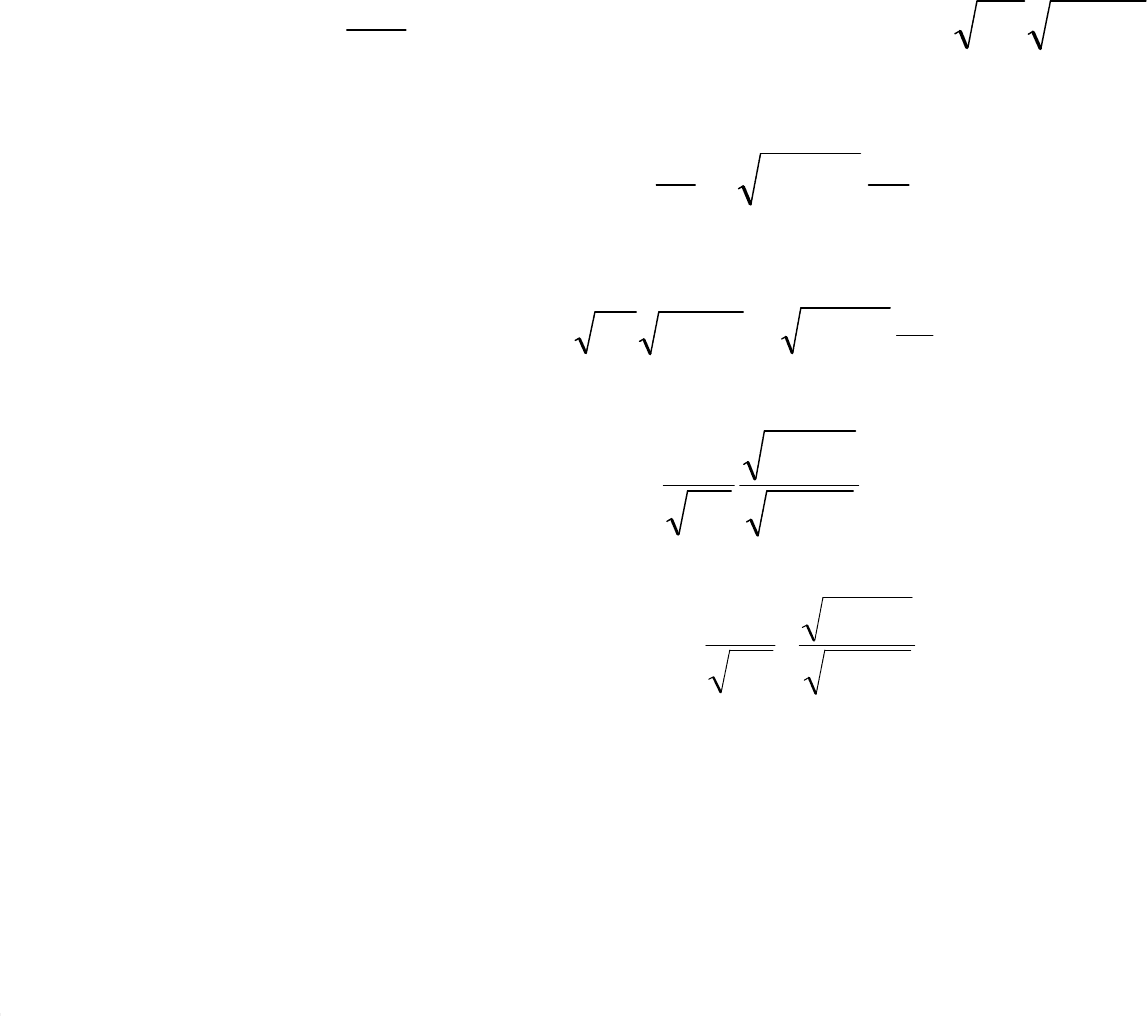
Тогда
, ; .
Сдругойстороны, скоростьестьпроизводнаяотпутиповремени
.
Сравниваяформулыдляскоростей, получим
,
откуда
,
ивремяскатаизположенияА
1
вположениеА
2
определитсяпоформуле
( )
yymg
mv
−=
1
2
2
(
)
yygv −=
1
2
2
yygv −=
1
2
dt
dx
y
dt
ds
v
2
1
′
+==
dt
dx
yyyg
2
1
12
′
+=−
dx
yy
y
g
dt
−
′
+
=
1
2
1
2
1
dx
yy
y
g
dtT
x
x
x
x
∫∫
−
′
+
==
2
1
2
1
1
2
1
2
1

Функционал
Нетрудноуяснитьобщиечертыприведенныхзадач. Преждевсего, всеони
являютсязадачаминаэкстремум – максимумиминимум. Ранеемырешализадачина
экстремумсредствамидифференциальногоисчисления. Еслизадачасводиласьк
рассмотрениюэкстремумафункции f(x) одногопеременного, тоискомымбылозначение
x–этозадачасоднойстепеньюсвободы. Еслинадобылонайтиэкстремумфункции
от n переменных, тоискомымбылнаборзначений – этозадачасn
степенямисвободы. Врассмотренныхвышезадачахискомойявляетсялиния, или
функция, откоторойтребуетсятолько, чтобыонаудовлетворялазаданнымграничным
условиям. Ноприпроизвольномвыборетакойфункцииимеетсябесконечноечисло
степенейсвободы; такимобразом, можносказать, что вариационноеисчислениеизучает
экстремумывзадачахсбесконечнымчисломстепенейсвободы.
Ксказанномувозможенещётакойподход. Рассмотрим, любойизинтегралов
(1)-(3). Есливнеговместо y(x) подставитьлюбуюфункцию y(x), заданнуювуказанных
пределахиудовлетворяющуюграничнымусловиям, тоонприметопределенное
численноезначение.
Закон, покоторомукаждойфункцииизнекоторогоклассафункцийставитсяв
соответствиеопределенноечисло, называетсяфункционалом. Задачасостоитв
подборефункции у(х), длякоторойинтегралпринимаетэкстремальное (максимальное
или минимальное) значение. Таким образом, вариационное исчисление изучает
экстремумыфункционалов.
(
)
n
xxxf ,...,,
21
n
xxx ,...,,
21

Приведемнесколькоконкретныхпримеровфункционалов.
Пусть
(4)
Этотфункционалопределендлявсехфункций y(x), заданныхпри 0≤x≤2 и
принимающихтамконечныезначения (илидажебесконечные, еслиинтегралполучится
сходящимся). Например,
дляфункции y=x
2
(0≤ x ≤2) получится ;
y=sin x (0≤ x ≤2)
{}
∫
==
2
0
2
dxyyII
∫
==
2
0
4
4,6dxxI
;19,1
4
4sin
1 =−=I
4
1
x
y =
38,222 ==I
