Презентация - Семенкин Е.С. Методы оптимизации
Подождите немного. Документ загружается.


Как видно из описания постановок задач вариационного исчисления в
конкретныхзадачахчасторассматриваетсяэкстремумфункционаланесредивсех
функций, составляющихопределенноефункциональноепространство, атолько
средифункций, удовлетворяющихнекоторымдобавочнымлинейнымнеоднородным
условиям, например
. (19)
Вэтомслучаеусловие (18) должновыполнятьсядлялюбойвариации δу,
удовлетворяющейсоответствующимоднороднымусловиям, т.е. дляусловий (19)
, .
Всамомделе, длятаких δу функция y+kδy такжеудовлетворяетусловиям (19),
апотомуможноповторитьтожедоказательство, чтобылоприведеновышедля (18).
Линейные неоднородные условия определяют в пространстве (R)
гиперплоскость (речьидетогиперплоскостяхвбесконечномерномфункциональном
пространстве)
.
Если
ставится
задача
об
экстремуме
функционала
на
некотором
,)(
a
yay
=
b
yby
=
)(
0)(
=
ay
δ
0)(
=
by
δ
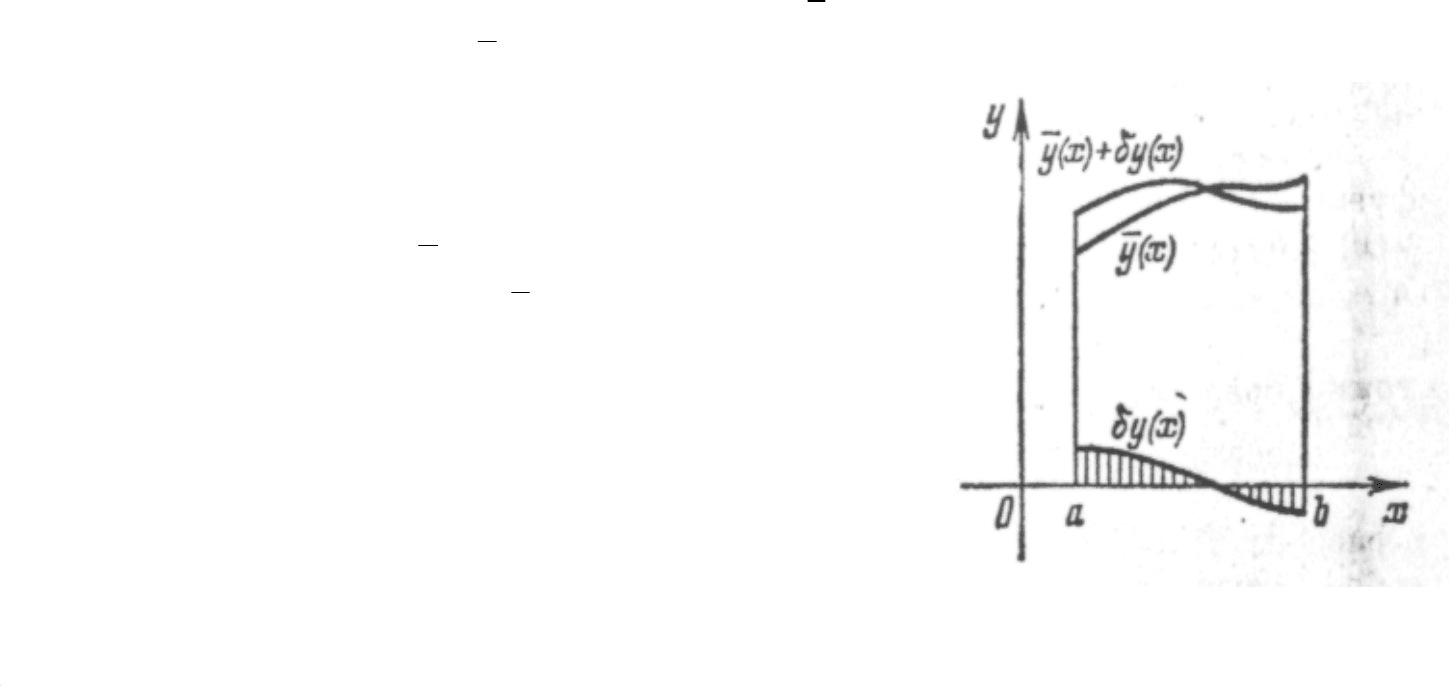
Вариация функционала
Вариацияодноизцентральныхпонятийприизучениинелинейныхфункционалов,
оноиграеттужероль, чтопонятиедифференциалаприизучениинелинейныхфункций.
Дифференциалнелинейнойфункцииравенглавнойлинейнойчастиееприращения,
заменаприращениянадифференциалозначаетлинеаризациюфункциипрималом
измененииаргумента;
Вариациянелинейногофункционаларавнаглавнойлинейнойчастиегоприращения,
заменаприращениянавариациюозначаетлинеаризациюфункционалаприпереходеот
однойфункции (откоторойзависитзначениефункционала) кдругой, близкойфункции.
Рассмотрим, например, функционал (4). Пустьфункция y(x), откоторойзависитего
значение, сначаласовпадаласнекоторой , азатеммыперешликнекоторойдругой,
близкойфункции .
(
)
xy
(
)
(
)
xyxy δ+
Здесь - это вариация
функции у(х), т.е. произвольная функция,
мало уклоняющаяся от нуля и добавляемая к
исходной функции для получения новой,
проварьированной функции (см. рисунок).
(Приэтоммалоеуклонениеотнуляпонимаетсяв
смыслетойнормы, котораяпринятазаоснову,
например, нарисункемалостьпонимаетсявсмысле
С
1
).
(
)
xy
δ
(
)
xy
(
)
(
)
xyxy δ+

Припереходеот к функционал (4) получитприращение
∆I .(10)
Пустьтеперьфункция зафиксирована, афункцию можновыбирать
произвольно. Мывидим, чтотогда∆Iсостоитиздвухчастей, каждаяизкоторых
представляетсобойфункционалотносительно . Перваячасть
(11)
обладаетсвойствомлинейностипо δу, т.е. этолинейныйфункционал, тогдакак
втораячасть
прималых δу имеетвысшийпорядокмалости. Такимобразом,(11) представляет
собойглавную (т. е. сточностьюдочленавысшегопорядкамалости) линейнуючасть
приращения (10) функционала (4) припереходеот к . Выражение (11)
иназывается (первой) вариациейδIфункционала; можнонаписать
(
)
xy
(
)
(
)
xyxy δ+
{ } {}
[ ]
() () ()
[ ]
∫∫∫∫
+⋅=−+=−+=
2
0
2
2
0
2
2
0
2
0
2
2 dxxydxxyxydxydxyyyIyyI δδδδ
(
)
xy
(
)
xy
δ
yyy −=δ
() ()
dxxyxy δ⋅
∫
2
0
2
()
[ ]
∫
2
0
2
dxxyδ
(
)
(
)
xyxy δ+
() ()
dxxyxydxyI
∫ ∫
⋅==
2
0
2
0
2
2 δδδ
(
)
xy
(
)
xy

Разобранныйпримерявляетсятипичным. Еслизаданпроизвольныйфункционал
I{у} имыпереходимотфункции у(х) кфункции у(х)+ δу(х), то, какправило,
приращениефункционала
можнопредставитьввидесуммыдвухслагаемых
(12)
первоеизкоторыхпрификсированнойфункции у(х) представляетсобойлинейный
функционалотносительно δу(x), автороеимеетотносительно δу(x) высшийпорядок
малости. Тогдапервоеслагаемое, вправойчасти (12) иназывается вариацией
функционала I, т. е.
Вслучаях, когдаслагаемымвысшегопорядкамалостиможнопренебречь, можно
сказатьпросто, чтовариацияфункционала – этоегобесконечномалоеизменение, т.е.
изменение, полученноезасчетбесконечномалойвариациифункции, откоторой
зависитэтотфункционал. Заменаприращенияфункционаланаеговариациюозначает
линеаризацию этого функционала, аналогично рассуждениям, приводимым при
введении
понятия
дифференциала
функции
.
}
{
}
{
y
I
y
y
I
I
−
+
=
∆
δ
},
;
{
}
;
{
11
y
y
R
y
y
I
I
δ
δ
+
=
∆
};{
1
yyII δδ =

Пусть, например, рассматриваетсяфункционалвида
, (13)
гдевпроцессеинтегрирования y считаетсязависящимот х, у=у(х). Тогда
. (14)
Но, таккак {членывысшегопорядкамалости},
то, подставляяв(14) иотбрасываяэтичлены, получим
(15)
Дляфункционала
(16)
аналогично получаем
∫
=
b
a
dxyxFyI ),(}{
∫
−+=∆
b
a
dxyxFyyxFI )],(),([ δ
(
)
(
)
(
)
+
′
+=+ yyxFyxFyyxF
y
δδ ,,,
( ) ( )
ydxyxFdxyxFI
b
a
y
b
a
δδδ
∫∫
′
== ,,
{} ( )
dxyyxFyI
b
a
∫
′
= ,,
( ) ( )
[ ]
dxyyyxFyyyxFI
b
a
yy
∫
′′′
+
′′
=
′
δδδ ,,,,
y
′
δ
(
)
y
′
δ
( )
′
yδ

Необходимое условие экстремума
Это условие совершенно аналогично необходимому условию экстремума
функцииоднойилинесколькихпеременных. Допустим, чтонекотораяфункция .
реализуетлокальныймаксимумилиминимумфункционала I{у} ввыбранном
функциональномпространстве (R), причемэтотфункционалимеетвариацию ,
т. е. допускаетвблизи линеаризацию. Крометого, будемсчитать, что
рассматривается внутренний (не граничный) экстремум, т.е. функционал I{у}
определендля всеху,достаточноблизкихк всмыслевыбраннойнормы; этобудет
предполагатьсявсюдудалее, еслинеоговоренопротивоположное.
Тогдадлялюбой должнобыть
. (18)
Всамомделе, пустьдляопределенностипри функционал I имеет
минимуми >0 длянекоторой . Подставимв(12) kδy вместо δу, где k -
скаляр: получим
Однако
при
малых
|
k|
левая
часть
должна
быть
положительной,
а
правая
имеет
(
)
xy
};{ yyI δδ
(
)
xyy =
y
(
)
Ry
∈
δ
0};{ =yyI δδ
(
)
xyy =
};{ yyI δδ
y
δ
});{
1
};{(};{};{}{}{
_
1
_
1
_
1
_
1
__
ykyR
k
yyIkykyRykyIyIykyII δδδδδ +=+=−+=∆

Как видно из описания постановок задач вариационного исчисления в
конкретныхзадачахчасторассматриваетсяэкстремумфункционаланесредивсех
функций, составляющихопределенноефункциональноепространство, атолько
средифункций, удовлетворяющихнекоторымдобавочнымлинейнымнеоднородным
условиям, например
. (19)
Вэтомслучаеусловие (18) должновыполнятьсядлялюбойвариации δу,
удовлетворяющейсоответствующимоднороднымусловиям, т.е. дляусловий (19)
, .
Всамомделе, длятаких δу функция y+kδy такжеудовлетворяетусловиям (19),
апотомуможноповторитьтожедоказательство, чтобылоприведеновышедля (18).
Линейные неоднородные условия определяют в пространстве (R)
гиперплоскость (речьидетогиперплоскостяхвбесконечномерномфункциональном
пространстве)
.
Если
ставится
задача
об
экстремуме
функционала
на
некотором
,)(
a
yay
=
b
yby
=
)(
0)(
=
ay
δ
0)(
=
by
δ
Уравнение Эйлера
Вомногихзадачахудается, пользуясьнеобходимымусловиемэкстремума, найти
искомоерешение у(x). Однакоформа (18) этогоусловиянесовсемудобна, таккакона
включает в себя произвольную функцию δу. Поэтому необходимое условие
преобразуюткдругой, равносильнойформе, содержащейтолькоискомоерешение.
Такоепреобразованиеразличнодляразныхклассовфункционалов, и дальнейшее
содержание восновном посвященорассмотрениюэтихклассов. Необходимоеусловие,
получающеесядлярешения, обычносостоитиздвухчастей: из уравненияЭйлера
(обычнодифференциального), которомурешениедолжноудовлетворятьвнутриобласти
своегоопределения, ииздобавочныхграничныхусловий, которыемогутбытьчастично
заданызаранее, ачастично – выведеныизусловия (18).
Функционал (16), значениякоторогомыбудемсравниватьдлявсехнепрерывно
дифференцируемыхфункций у(х), удовлетворяющихзаданнымграничнымусловиям
у(а)=у
a
, у(b)=у
b
. (19)
Наоснованииформул (18) и (17) получаем, чтодолжнобыть
(20)
∫
=
′′′
+
′′
′
b
a
yy
dxyxyxyxFyxyxyxF 0]))(),(,())(),(,([ δδ
],[
1
baCy
∈
δ
у и от х. Длядоказательстваэтогообозначимнаминутувыражениевфигурных
скобкахчерез ϕ(х). Если ϕ(а)=ϕ(b)=0, томожнопростоположить δу=ϕ(х) наинтервале
а+ε≤х≤b–ε, где ε >0 весьмамало, акточкам х=а и х=b значение ϕ(х) спадаетдонуля.
Чтобывыяснитьотсюда, какомууравнениюдолжнаудовлетворятьфункция ,
проинтегрируемвторойчлен (20) почастям:
, (21)
таккаквсилуусловий , , проинтегрированныйчленравеннулю.
Подставляя (21) в (20) получаем
)(xy
∫
=
′′′
′
b
a
y
dxyxyxyxF δ))(),(,(
∫ ∫
′′
−=
′′′
−
′′
=
′′
=
′
b
a
b
a
yy
b
axy
ydxxyxyxFydxxyxyxFyxyxyxF δδδ ))](),(,([]))(),(,([]))(),(,([
0)(
=
ay
δ
0)(
=
by
δ
.
Ноотсюдаследует, чтовыражениевфигурныхскобкахтождественноравнонулю
при а≤x≤b т. е. всокращённойзаписи
(22)
гдепод понимаетсяполнаяпроизводная, составленнаясучётомзависимости
∫
=
′′′′
−
′′
′
b
a
yy
dxyxyxyxFxyxyxF 0}]))(),(,([))(),(,({ δ
0=
′
−
′
′
yy
F
dx
d
F
dx
d
y
′
∫
=
b
a
dxx 0)]([
2
ϕ
Устремляя ε к нулю, мы опять приходим к , а оттуда к (22).

Еслираскрытьвыражениеполнойпроизводнойпоформулепроизводнойсложной
функции (иписать у вместо ), мыполучим
(23)
Мывидим, чтоэтообыкновенноедифференциальноеуравнениевторогопорядка.
ВсякоерешениеуравненияЭйлера (23) называется экстремалью функционала
(16), онопридаетэтомуфункционалустационарноезначениевследующемсмысле:
если у(x)–любоетакоерешение, взятоенанекотороминтервале a
1
≤ x ≤b
l
(a ≤ a
1
<b
1
≤b);
вчастности, можетбыть а
1
=a, b
1
=b иеслипроизвольнопроварьировать у(х) наэтом
интервале, неменяязначения y(a
1
) и y(b
1
), то
.
Экстремаляминазываютсятакжеграфикирешений, т. е. интегральныелинии
уравнения.
Совокупность экстремалей, как общее решение обыкновенного
дифференциального уравнения второго порядка, образует двухпараметрическое
семействофункций. Двухграничныхусловий (19) впринципекакраздостаточнодля
отыскания
требуемых
частных
решений
.
Правда,
уравнение
Эйлера
редко
y
′
0),,(),,(),,(),,(
=
′
′
′
′
′
−
′
′
′
′
−
′
′
′
−
′
′
′′′′
yyyxFyyyxFyyxFyyxF
yyyyyxy
∫
=
′
1
1
0),,(
b
a
dxyyxFδ
