Презентация - Семенкин Е.С. Методы оптимизации
Подождите немного. Документ загружается.


ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Динамическоепрограммированиеявляетсяещеоднимиздвухсовременных
направленийвтеориизадачуправления. Методдинамическогоуправленияможет
применятьсянепосредственноприрешенииобщейзадачиуправления:
= + F(x
1
, t
1
),
x' = f(x(t), u(t), t),
x(t
0
)=x
0
,x(t
1
)=x
1
,{u(t)}∈U. (1)
Сущность подхода динамического программирования состоит в следующем:
даннаяконкретнаязадачуправления "погружается" вболееширокийклассзадач,
которыехарактеризуютсярядомпараметров; затемспомощьюцентральногопринципа
–"принципаоптимальности"–определяетсяосновноерекуррентноесоотношение,
связующеезадачиизэтогокласса. Есливыполненынекоторыедополнительные
предположенияотносительногладкостиучаствующихврассмотрениифункций, тоиз
главногорекуррентногосоотношениявытекаетосновноедифференциальноеуравнение
вчастныхпроизводных – уравнениеБеллмана,-решаякотороеможнонайтирешение
вышеупомянутого
широкого
класса
задач
.
Jmax
t })({u
∫
1
0
) ),( ),((
t
t
dttttI ux
Принцип оптимальности и уравнение Беллмана
Формулировкапринципа оптимальности:"Оптимальноеповедениеобладаеттем
свойством, что, каковыбынибылипервоначальноесостояниеирешение (т.е. управление) в
начальныймомент, последующиерешениядолжнысоставлятьоптимальноеповедение
относительносостояния, получающегосяврезультатепервогорешения".
Доказательство необходимости принципа оптимальности можно легко получить,
рассуждаяотпротивного: есливынеиспользуетенаилучшимобразомто, чемвы
располагаете, товыникогданераспорядитесьнаилучшимобразомитем, чтовымоглибы
иметьвдальнейшем.
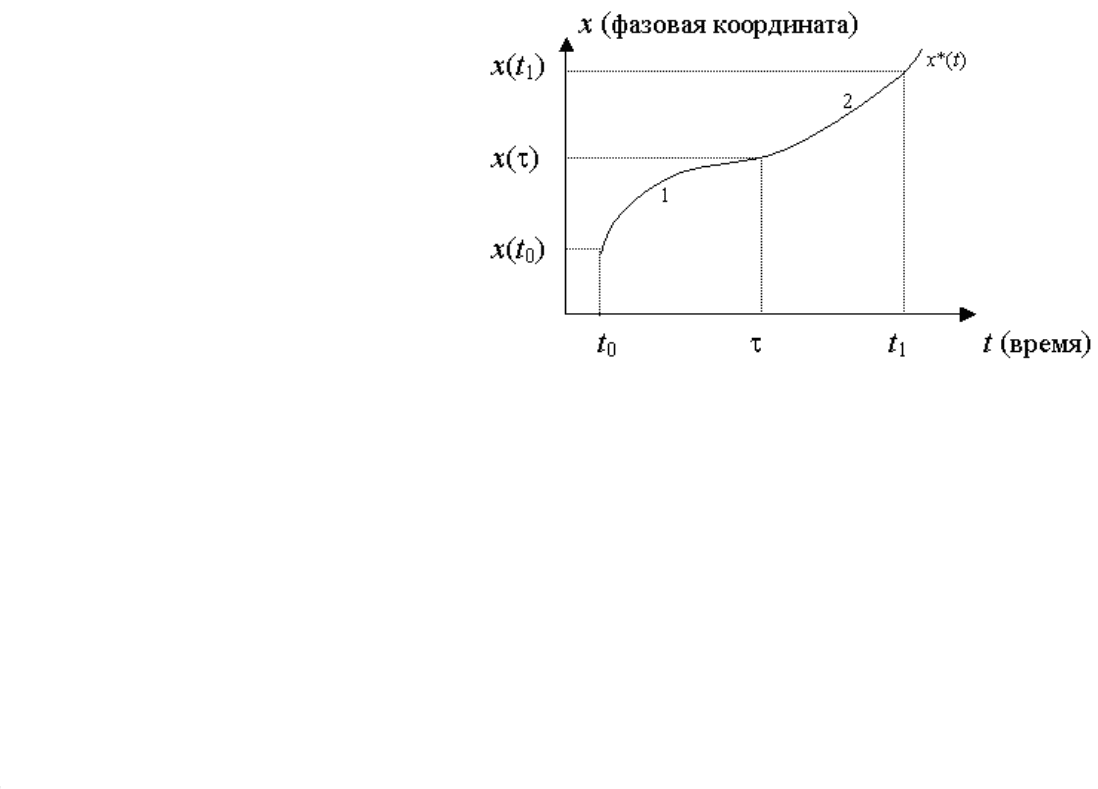
Нарисункеданаиллюстрацияпринципанапримерезадачисоднойфазовой
координатой. Кривая x*(t)(t
0
≤t≤t
1
)–этофазоваятраектория, соответствующаяоптимальному
управлению, начальноеиконечноесостояния – фиксированы. Всятраекторияподеленана
двечастиотносительномоментавремени τ. Согласнопринципуоптимальности, траектория
2, определеннаяпри τ≤t≤t
1
, должнапредставлятьсобойоптимальнуютраекториюпо
отношениюкначальномусостоянию x(τ). Следовательно, втораячастьоптимальной
траекториисамапосебедолжнабытьоптимальнойтраекторией, внезависимостиоттого,
чтопроисходилоссистемойдотого, каконапришлаксостоянию, являющемусяначальным
длявторойчаститраектории.

Предположим, чтообщаязадачауправления (1) имеетрешение.
Максимальноезначениецелевогофункционалазадачисначальнымсостоянием x
иначальнымвременем t
J*(x, t)
назовем функциейоптимальногоповедения.
Отметим, чтовтовремякак J представляетсобойфункционал, зависящийот
{u(t)}, J* являетсяфункцией, зависящейот n+1 параметров x и t.
Такимобразом, задачаоказывается "погруженной" вболееширокийклассзадач,
характеризуемых значениями n+1 начальных параметров. Оптимальной значение
целевойфункцииисходнойзадачи (1) имеет, такимобразом, вид
J*=J*(x
0
, t
0
).
Если J*(x, t) являетсяфункциейоптимальногоповедениядлязадачисначальным
состоянием x вмомент t, то, согласнопринципуоптимальности J*(x+∆x, t+∆t) является
функциейоптимальногоповедениядлявторойчастиоптимальнойтраекториис
начальныммоментомвремени t+∆t иначальнымсостоянием x+∆x. Посколькуприрост
функцииоптимальногоповедениянапротяжениивсегопромежуткавременимежду t и
t+∆t можетпроисходитьтолькозасчетизмененияподынтегральнойфункции, тоон
равен
I
(
x
,
u
,
t
)
∆
t
.
Значения
функции
оптимального
поведения
на
всем
интервале
времени,
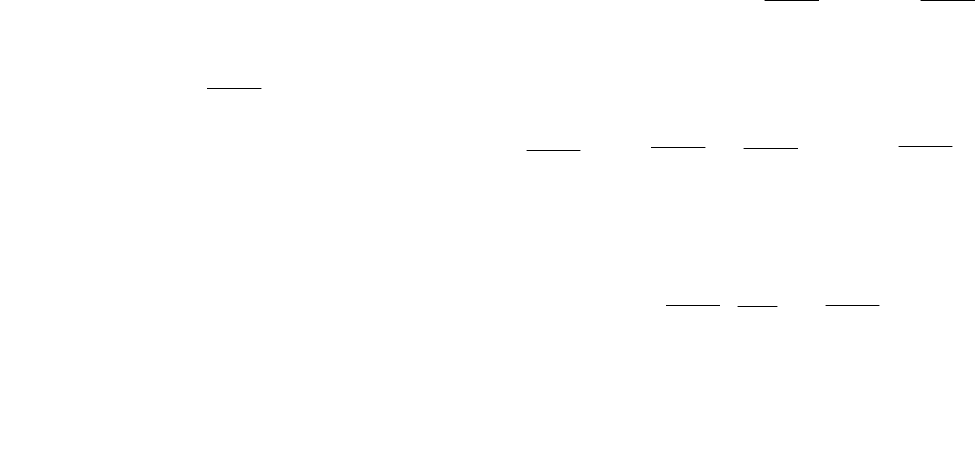
Такимобразом, приходимкосновномурекуррентномусоотношению
J*(x, t)= {I(x,u,t)⋅∆t + J*(x+∆x, t+∆t)} (2)
Вдинамическомпрограммированиисущественнуюрольиграетпредположение,
чтофункцияоптимальногоповедения J*(x, t) представляетсобойоднозначнуюи
непрерывнодифференцируемуюфункциюот n+1 переменных. Иначеговоря, решения
задачболееширокогоклассаявляютсяоднозначнымиинепрерывнымифункциями
относительноизмененийначальныхпараметров.(Отметим, чтовомногихзадачахэти
предположенияогладкостиневыполняются, крометого, заранеевообщенеизвестно,
будутлионивыполненывданнойконкретнойзадаче).
Благодаряэтомупредположениюможноразложить J*(x+∆x, t+∆t) вточке (x, t) по
формулеТейлора:
J*(x+∆x, t+∆t)=J*(x, t)+ ∆x+ ∆t+… (3)
где - этовектор-строка
= ( , , …, ).
})({ t
max
u
x
∂
∂
*J
t
J
∂
∂
*
x
∂
∂
*J
x
∂
∂
*J
1
*
x
J
∂
∂
2
*
x
J
∂
∂
n
x
J
∂
∂
*
x
∂
∂
*J
t
∆
∆
x
t
J
∂
∂
*
})({ t
max
u

Так как второе слагаемое в (4) представляет собой скалярное произведение
вектора-строки и вектора-столбца f(x, u, t), то уравнение Беллмана можно записать
как
- = {I(x, u, t)+ f
j
(x, u, t)}.
Переходякпределупри ∆t → 0 сучетомтого, что
= x' = f(x, u, t),
получаем
- = {I(x, u, t)+ f(x,u,t)}. (4)
Уравнение (4) называется уравнением Беллмана и является основным
дифференциальным уравнением в частных производных, используемых в
динамическомпрограммировании.
t
t
∆
∆
→∆
x
0
lim
t
J
∂
∂
*
x
∂
∂
*J
x
∂
∂
*J
t
J
∂
∂
*
∑
=
∂
∂
n
j
j
x
J
1
*
})({ t
max
u
})({ t
max
u

СуравнениемБеллманасвязановкачествеграничногоусловияограничение,
налагаемоенаконечноесостояние:
J*(x(t
1
), t
1
) = F(x
1
, t
1
).
Этоусловиепоказывает, чтозначениефункцииоптимальногоповедениядля
задачи, начальным моментом и начальным состоянием которой являются
соответственноконечныймоментиконечноесостояние, равнозначениюфункции F,
рассчитанномувданныймоментвремениприданномсостоянии.
ЕслибыуравнениеБеллманабылорешено, томыполучилибыфункцию
оптимальногоповеденияи,следовательно, оптимальноезначениецелевойфункции
дляисходнойзадачиможнобылобыопределитькакчастноезначениеэтойфункции
приуказанныхвформулировкезадачиконкретныхначальныхусловиях. Однаков
общемслучаеэтоуравнениевчастныхпроизводныхпервогопорядка, какправило,
нелинейное, неимеетаналитическогорешения. Впринципеможнорешатьуравнения
Беллмана, представленные в виде разностных схем, на ЭВМ с большим
быстродействием. ОднакодажесовременныеЭВМ, работающиесвысокойскоростью
счета, необладаюттакоймашиннойпамятью, котораяпозволялабынайтидостаточно
хорошееприближениекрешениюдажепринеоченьбольшихразмерностях. Беллман
назвал
это
препятствие
"проклятьем
размерности"
("
curse
of
dimensionality
")
.

Решение многошаговых задач оптимизации методом
динамического программирования
Вомногихдинамическихзадачахвремярассматриваетсянекакнепрерывная, акак
дискретнаявеличина. Задачитакоготипаназываются многошаговымизадачами
оптимизации. Онимогутрешатьсяметодомдинамическогопрограммирования.
Рассмотримнекоторуюдинамическуюсистему S.
Пустьна k-мшаге (k=1,2,...,n) состояниесистемыопределяетсясовокупностью
чисел (фазовымикоординатами) X
k
=( ), которыеполученыврезультатереализации
управления U
k
, обеспечивающегопереходсистемы S изсостояния X
k-1
всостояние X
k
.
Будемполагать, что X
k
зависитот X
k-1
и U
k
инезависитоттого, каксистемапришлав
состояние X
k-1
(свойство отсутствияпоследействия).
Пусть W
k
(X
k-1
, U
k
) естьдоход (выигрыш), полученныйврезультатереализации k-го
шага. Тогдаобщийвыигрышполагаемравным
F= W
k
(X
k-1
, U
k
)
(свойство аддитивностицелевойфункции).
Совокупностьуправлений U
*
=( , ,..., ), врезультатереализациикоторых
система
S
переходит
за
n
шагов
из
начального
состояния
X
0
в
конечное
X
n
и
при
этом
k
m
kk
xxx ,...,,
21
∑
=
n
k
1
*
1
u
*
2
u
*
n
u

ПринципоптимальностиБеллмана.
Каковобынибылосостояниесистемыпередочереднымшагом, надовыбрать
управлениенаэтомшагетак, чтобывыигрышнаданномшаге плюсоптимальный
выигрышнавсехпоследующихшагах былбымаксимальным.
Оптимальнуюстратегиюможнополучить, еслисначаланайтиоптимальную
стратегиюуправлениянапоследнем n-мшаге, затемнадвухпоследнихшагахит.д.
вплотьдопервогошага.
Такимобразом, решениезадачидинамическогопрограммированияцелесообразно
начинатьсопределенияоптимальногорешениянапоследнем n-мшаге.
Длятого, чтобынайтиэторешение, нужносделатьвсевозможныепредположения
отом, какмогзакончитьсяпредпоследнийшагисучетомэтоговыбратьуправление ,
обеспечивающеемаксимальноезначениефункции W
n
(X
n-1
, U
n
). Такоеуправление ,
выбранноеприопределенныхпредположенияхотом, какокончилсяпредыдущийэтап,
называется условнооптимальным.
ПринципоптимальностиБеллманатребуетнаходитьнакаждомшагеусловно
оптимальныеуправлениядлялюбогоизвозможныхисходовпредыдущегошага.
Обозначим
через
F
(
X
0
)
максимальный
доход,
получаемый
за
n
шагов
при
переходе
0
n
u
0
n
u

Тогда
F
n
(X
0
)= [W
1
(X
0
, U
1
)+W
2
(X
1
,U
2
)+...+W
n
(X
n-1
, U
n
)],
F
n-k
(X
0
)= [W
k+1
(X
k
, U
k+1
)+F
n-k-1
(X
k+1
)],
Последнее соотношение называется основным функциональным уравнением
Беллмана и представляет собой математическую формулировку принципа
оптимальности.
Положим k=n-1. Тогда
F
1
(X)= [W
n
(X
n-1
, U
n
)+F
0
(X
n
)], (*)
где F
0
(X
n
) считаемизвестным.
Используя (*) ирассматриваявсевозможныедопустимыесостояния
X
1
n-1
, X
2
n-1
,...,X
l
n-1
,...,системына (n-1)-мшагенаходимусловно-оптимальные
управления u
n
0
(X
1
n-1
), u
n
0
(X
2
n-1
),...,u
n
0
(X
l
n-1
),...,исоответствующиезначенияфункции
(*):
F
1
0
(
X
1
n-1
),
F
1
0
(
X
2
n-1
),...,
F
1
0
(
X
l
n-1
), ... .
k
max
u
.1,0 −= nk
n
max
u
1+k
max
u

Переходимкрассмотрениюфункциональногоуравненияпри k=n-2.
F
2
(X
n-2
)= [W
n-1
(X
n-2
, U
n-1
)+F
1
(X
n-1
)], (**)
Длятого, чтобынайтизначение F
2
длявсехдопустимыхзначений X
n-2
, очевидно,
необходимознать W
n-1
(X
n-2
, U
n-1
) и F
1
(X
n-1
). Но F
1
(X
n-1
) мыужеопределилина
предыдущемшаге. Поэтомунужнопроизвестивычислениядля W
n-1
(X
n-2
, U
n-1
) при
некоторомнаборедопустимыхзначений X
n-2
исоответствующихуправлений U
n-2
. Эти
вычисленияпозволятопределитьусловнооптимальноеуправление U
0
n-1
длякаждого
X
n-2
. Каждоеизтакихуправленийсовместносужевыбраннымуправлениемна
последнемшагеобеспечиваетмаксимальноезначениедоходана двухпоследних шагах.
Последовательноосуществляяэтотитерационныйпроцесс, дойдем, наконец, до
первогошага. Наэтомшагенамизвестно, вкакомсостоянииможетнаходитьсясистема
(вначальном). Поэтомууженетребуетсяделатьпредположенияодопустимых
состоянияхсистемы, аостаетсялишьтольковыбратьуправление, котороеявляется
наилучшимсучетомусловнооптимальныхуправлений, ужепринятыхнавсех
последующихшагах.
1-n
max
u
