Презентация - Андреев В.К. Механика жидкости и газа
Подождите немного. Документ загружается.

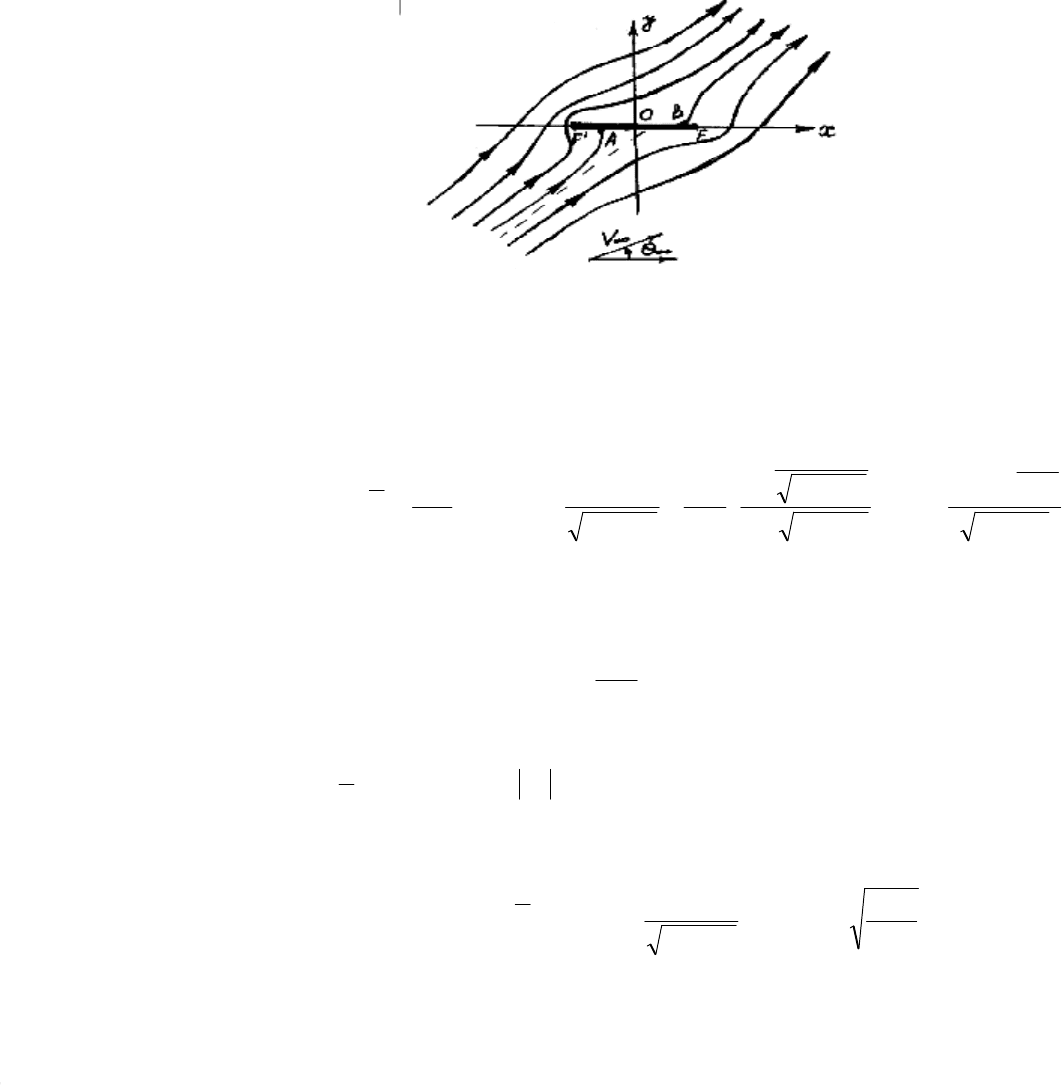
Рис. 12.6
Нулевая линия тока состоит из поверхности пластинки и двух отрезков софокусной гиперболы,
параметры которой зависят от угла атаки
∞
θ . Вычисляя скорость по (12.17), находим
2222
22
22
2
1
2
cz
i
ziv
u
czz
cz
z
i
cz
z
ivu
dz
dW
V
−
Γ
−
−=
−+
−
+
⋅
Γ
+
−
−==
∞
∞∞∞
π
π
. (12.18)
Для произвольной циркуляции Г при
c
z
±
=
скорость имеет бесконечные значения (на передней и
задней кромках). Найдем Г
из условия конечности скорости на задней кромке (согласно постулату
Жуковского
- Чаплыгина)
0
2
=
Γ
−
∞
i
civ
π
, т.е.
∞
−=Γ cvπ2 . (12.19)
Это выражение совпадает с величиной Г
, найденной по общей формуле (12.11), в которой для
нашего случая .sin,0,
2
1
0 ∞∞∞∞
=== θε Vvm
Подставляя выражение (12.19) в (12.18), получим следующую формулу распределения скоростей
:
.
22
cz
cz
viu
cz
cz
viuV
+
−
−=
−
−
−=
∞∞∞∞
(12.20)

На задней кромке скорость конечна и равна
∞
u
(реализуется плавное обтекание задней кромки), на
передней кромке )( cz
−
=
скорость остается равной бесконечности. Выбором циркуляции нел
ьзя сделать
скорость конечной на обеих острых кромках.
Лекция 16.
§13. Одномерные движения газа
Если все динамические и термодинамические величины газового потока являются функциями
только одной, в общем случае криволинейной, координаты и времени, то та
кой поток называется
одномерным. Для одно
мерных потоков существенно упрощаются все исходные уравнения, что
позво
ляет упростить учет и анализ влияния различных внешних воздействий на структуру потоков. К
таким воздействиям можно отнести подвод или отвод теп
лоты, массы, механической работы,
конденсацию, испарение и т.д.
Одномерным можно считать течение газа в канале с плавно изменяю
щимся поперечным сечением
и малой кривизной его оси. Вводится также допущение о постоянстве всех параметров потока в
поперечном сечении каналов, либо вместо действительных величин ис
пользуются их осредненные
значения.
Скорость звука
. Для выяснения особенностей движения газа важно сравнить скорость его
движения с характерной для данного газа и зависящей от его термодинамического с
остояния скоростью
распространения малых возмущений по газу (скоростью распространения звука).
Рассмотрим для простоты баротропный поток идеального политропного газа, все линии тока
которого параллельны оси Ox , а составляющая скорости
u
, давление
p
, плотность
ρ
и температура
T
являются функциями только от
x
и
t
, при этом пренебрегаем действием объемных сил.
Уравнения
движения и уравнение неразрывно
сти сводятся в этом случае к нелинейной системе дифференциальных
уравнений
1
,
()0
uup
u
txx
u
tx
ρ
ρ
ρ
∂∂∂
+=−
∂∂∂
∂∂
+=
∂∂
(13.1)
с тремя неизвестными
ρ
,
,
p
u
. Для баротропного движения система замыкается уравнением св
язи между
p
и
ρ
, в более общем случае необходимо добавить уравнение энергии и ура
в
нение состояния
Обратимся к решению простейшей задачи о распространении в газе малых возмущений
, которая
формулируется следующим образом: в покоящемся идеальном политроп
ном газе создаются весьма
малые возмущения скоростей, давлений и плотности, причем возникающее вследствие этого движение
является одномерным баротропным движением, зависящим лишь от координаты
x
и времени
t
;
требуется определить элементы возму
щенного движения. Для политропного газа давление зависит
только от плотности (в случае изоэнтропических движений, соотношение (4.8)),
k
Ap ρ= .
В покоящемся газе 0,,
00
=== upp ρρ , в возмущенном движении
'
0
'
0
'
,, ρρρ +=+== pppuu , (13.2)
где
0
'
0
''
,,1 ρρ <<<<<< ppu . Подставляя (13.2) в (13.1) и оставляя величины первого по
рядка малости,
получим
.0
,0)(
1
'
0
'
'
0
'
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
x
u
t
xd
pd
t
u
ρ
ρ
ρ
ρρ
(13.3)
Здесь учли соотношени
е, получающееся для баротропной жидкости с точностью до малых
величин первого порядка
xd
pd
xd
pd
x
p
∂
∂
=
∂
∂
=
∂
∂
'
0
)(
ρ
ρ
ρ
ρ
.
Система уравнений (13.3) является линейной (классическая система уравнений акустики). Так как
показатель адиабаты 1>=
v
p
C
C
k , плотность 0
>
ρ
, то 0>
ρd
pd
. Введем обозначение
2
00
)( a
d
pd
=
ρ
(13.4)

и перепишем систему (13.3):
tx
u
x
a
t
u
∂
∂
−=
∂
∂
∂
∂
−=
∂
∂
'
'
0
'
2
0
'
0
,
ρ
ρ
ρ
ρ . (13.5)
Систему (13.5) можно привести к следующему одному волновому уравнению (дифференцир
уя
первое уравнение по
t
, а второе – по
x
):
0
2
'2
2
0
2
'2
=
∂
∂
−
∂
∂
x
u
a
t
u
. (13.6)
Аналогичное уравнение получается и для
'
ρ :
0
2
'2
2
0
2
'2
=
∂
∂
−
∂
∂
x
a
t
ρρ
.
Так как ,)()(
'2
0000
'
ρρρ
ρ
a
d
pd
ppp =−=−= то
0
2
'2
2
0
2
'2
=
∂
∂
−
∂
∂
x
p
a
t
p
.
Общее решение любого из этих уравнений можно представить в виде суммы двух произ
вольных
функций
)()(
0201
'
taxftaxfu −++= . (13.7)
Вид функций
1
f и
2
f зависит от начальных условий задачи.
Введем новые координаты
1
ξ и
2
ξ , связанные с
t
x
,
при помощи равенств
taxtax
0201
, −=+= ξξ
. (13.8)
Такое преобразование координат имеет простой кинематический смысл. Ось координат
11
ξO
расположена вдоль оси Ox и движется поступательно в сторону отрицательного направления оси Ox
со
скоростью
0
a
, точно так же ось
22
ξO
движется поступательно в сторону положительного на
правления
оси Ox с той же скоростью
0
a .
Решение (13.7) принимает вид
)()(
221
'
ξξ ffu += . (13.9)
Рассмотрим каждое слагаемое по отдельности, т.е. следующие два частных решения у
равнения
(13.6):
)
(
)
(
),
(
)
(
0
2
2
2
'
0
1
1
1
'
t
a
x
f
f
u
t
a
x
f
f
u
−
=
=
+
=
=
ξ
ξ
.
(13.10)

Полагая в этих решениях
1
const
ξ
=
или
2
const
ξ
=
, получим две системы плоских волн:
000
const,const
xatxat+=−= , (13.11)
представляющих две движущихся в противоположные стороны со скоростью
0
a
перпендикулярные оси
Ox плос
кости, каждая из которых несет постоянные, заданные начальными условиями значения
возмущений скорости, давления, плотности или температуры; такие волны называются простыми.
Общее решение уравнения (13.6) и аналогичных уравнений для возмущений давления и
плотности складываются из решений, соответствующих двум распространяющимся в проти
воположные
стороны простым волнам.
Общая для обеих волн скорость
0
a
называется скоростью распространения малых возмущений в
газе и определяется согласно (13.4) формулой
ρd
pd
a = . (13.12)
В этой формуле подстрочный индекс нуль, характеризующий невозмущенное состояние газа,
опущен, так как формула (13.12) верна и в случае движущегося газа, если под величиной
a
понимать
местную скорость рас
пространения малых возмущений относительно движущегося газа в данной точке
потока. К распространению малых возмущений в жидкостях и газах относится
распространение звука,
заключающееся в распространении волн слабого сжатия и разрежения. В связи с этим величину
a
называют скоростью звука.
Если предположить, что жидкость несжимаема (
const
ρ
=
), то в силу (13.12)
∞
=
a
. Это означает,
что в мо
дели несжимаемой жидкости возмущения распространяются с бесконечной скоростью, т.е.
всякое изменение давления в данном месте потока должно мгновенно сказаться в любом другом месте.
Число Маха. Скорость распространения малых возмущений или скорость звука служит
важной
характеристикой потока сжимаемой среды. В зависимости от то
го, будут ли скорости движения частиц
меньше или больше скорости звука, принципиально различными будут и происходящие в среде
явления. Если где-нибудь в потоке газа скорость V станет равна местной скорости звука
a
, то такая
скорость газа
**
aV = называется критической; кри
тическими будут называться и соответствующие
значения
***
,, Tp ρ
(давления, плотности и температуры). Нали
чие критических явлений представляет
характерную особенность газовых течений.
Отношение скорости V
движения газа в данной точке потока к соответствующей этой точке
местной скорости звука
a
V
M= , называется числом Маха (числом М). Для М <
1 поток в данной точке
дозвуковой, при М =1 – звуковой и для М >1 – сверхзвуковой.
Для адиабатических движений газа критические значения параметров состояния одина
ковы для
всех частиц газа. Отношение скорости потока в данной то
чке к одинаковой для всего потока в целом
критической скорости λ=
*
a
V
называется скоростным коэффициентом.
Лекция 17.
Основные уравнения одномерного потока
Для одномерных потоков характерно изменение всех параметров течения только в одн
ом
направлении. Это обстоятельство существенно упрощает все исходные уравнения. Одномерным можно
считать течение жидкости в канале с плавно изменяющимся поперечным сечением и малой кривизной
его оси. Одновременно вводится допущение о постоянстве всех парам
етров потока в поперечном
сечении канала (либо вместо действительных вели
чин используются их усредненные значения).
Полученные в рамках такой простей
шей модели решения носят приближенный характер, но во многих
случаях достаточно хорошо совпадают с опытными данными.
Уравнение одномерного течения являются частным случаем общих уравнений сохранения.
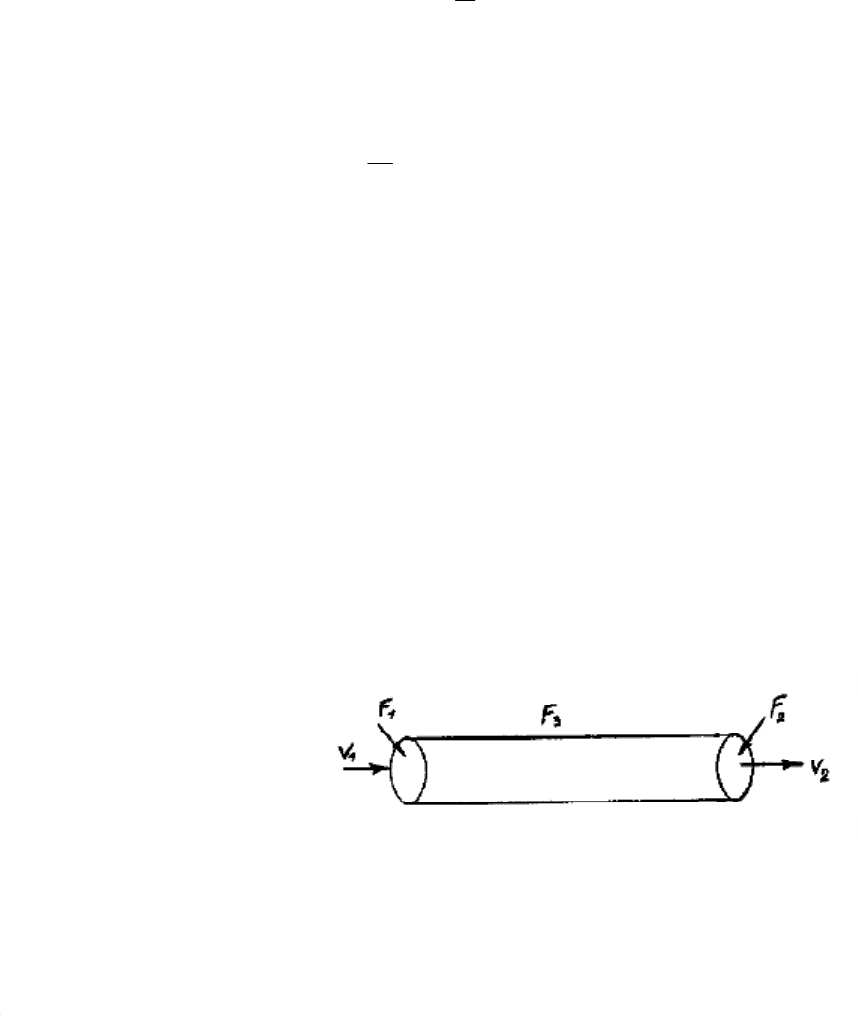
Уравнение неразрывности
Запишем уравнение неразрывности в интегральной форме для некото
рой трубки тока:
0
n
F
VdFρ
=
∫
.
Рис. 13.1

Здесь
321
FFFF ++= - площадь всей поверхности рассматриваемого объема (рис. 13.1),
n
V -
скорость жидкости, нормальная к элементу поверхности dF .
12
1112223
0(
так как 0)
nnn
FF
VdFVdFVdFρρ
−==
∫∫
.
Для одномерных течений скорость совпадает с направ
лением нормали к сечениям канала, поэтому
получаем уравнение расхода для одномерного течения в виде
const
VF
ρ
=
(13.13)
или для двух произвольных сечений канала:
222111
FVFV ρρ = .
Уравнение движения идеальной жидкости
Это уравнение для одномерного установившегося течения при отсутствии массо
вых сил имеет
вид:
).(.
2
,
1
2
Бернуллиинтегралconst
dpu
x
p
xd
ud
u
=+
∂
∂
−=
∫
ρ
ρ
(13.14)
Уравнение энергии
Для одномерного стационарного течения 0)
1
( =+
ρtd
d
p
td
ed
Для политропного газа:
.0
1)(
,}{
1
=−=+−
−===−=
−
xd
pd
xd
hd
xd
d
p
xd
pd
xd
hd
p
hTRpTRhe
ρ
ρρ
ρ
ρ
Тогда из (13.14) получаем
0
2
2
hh
u
=+ , (13.15)
где
0
0
00
1 ρ
p
k
k
Tch
p
−
== - энтальпия заторможенного потока;
000
,, Tp ρ
- параметры полного торможения.
Таким образом, уравнение энергии для сжимаемой идеальной жидкости имеет вид (13.15), или
0
0
2
112 ρρ
p
k
kp
k
kV
−
=
−
+ , (13.15 а)
0
2
2
TCTC
V
pp
=+ . (13.15 б)
Из уравнения (13.15) следует, что в установившемся энергоизолированном потоке сумма
кинетической и потенциальной энергии, отнесенной к единице массы движуще
йся жидкости, остается
постоянной вдоль трубки тока (или вдоль одномерного канала).
Из уравнения (13.15) следует, что скорость потока не может расти беспредельно, а ограничивается
некоторой максимальной величиной
max
V , которая достигаетс
я при полном переходе всей располагаемой
энергии в кинетическую.
Следовательно,
1
2
1
22
0
0
0
0max
−
=
−
==
k
kRTp
k
k
hV
ρ
, (13.16)
max
V называется максимальной скоростью. Эту скорость можно выразить и через скорость звука.
Для изоэнтропического течения
const
k
p
ρ
=
, отсюда

11
const
kk
k
dppkp
kk
d
ρρ
ρρρ
−−
===, т.е.
TkR
pk
d
pd
a ===
ρρ
. (13.17)
Следовательно, в силу (13.16) и (13.17), имеем
0
2
0
22
1
1
2
h
k
a
k
aV
=
−
=
−
+ . (13.18)
Отсюда
1
2
0max
−
=
k
aV . (13.19)
Максимальная скорость соответствует истечению в абсолютный вакуум (h=0, p=0, T=0).
Практически такая скорость недостижима, т.к. с приближением к
max
V
разрежение газа становится
очень большим и к рассматриваемому потоку уже неприменимы уравнения состоя
ния и энергии в
известной форме. Таким образом
, максимальная скорость является теоретическим пределом для
ско
рости газа. Если скорость потока равна местной скорости звука, то она называется критической
(
**
aV=
). Соответственно, сечение, гд
е эта скорость достигается, и параметры в этом сечении называют
критическими, т.е. в критическом сечении
*
VaV == .
Записывая (13.18) для критического сечения, получаем
,
1
1
2
2
0
2
*
2
*
−
=
−
+
k
a
k
VV
или
1
1
1
2
2
0
2
*
−
=
−
+
⋅
k
a
k
k
V
. (13.20)
Отсюда сле
дует, что критическая скорость, так же как максимальная, полностью определяется
параметрами торможения и выражается через них с помощью соотношений
0
00
0*
1
2
1
2
1
2
ρ
p
k
k
k
TRk
k
aV
+
=
+
=
+
= . (13.21)
В результате запишем уравнение энергии в виде
2
1
1
1
2
2
*
22
V
k
k
k
aV
−
+
=
−
+ . (13.22)
С помощью уравнения энергии выразим параметры потока в произвольном сечении трубки тока
(или канала) через параметры торможения и скорость в этом сечении. Из (13.22) следует:
2
2
*
2
2
1
1
2
1
1
1
2
1
V
V
k
k
k
V
a
−
+
=
−
+
. (13.23)
Преобразуем уравнение энергии (13.15б ), разделив его левую и правую части на TC
p
:
T
T
TC
V
p
0
2
1
2
=+ , так как
1
−
=
k
kR
C
p
, то .1
1
2
0
2
T
T
kRT
kV
=+
−
Поскольку kRTa =
2
(см. (13.17)),
)(,
2
1
1
2
0
a
V
MM
k
T
T
=
−
+=
. (13.24)
Используя уравнение состояния и уравнение изоэнтропы, находим:
1
0
0
0
1
0
1
0
0000
)()()()(
−
−
=====
kk
k
k
k
p
p
p
p
p
p
T
T
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
.
Отсюда
.)
2
1
1()(
,)
2
1
1()(
1
1
2
1
1
00
1
2
1
00
−−
−−
−
+==
−
+==
kk
k
k
k
k
M
k
T
T
M
k
T
T
p
p
ρ
ρ
(13.25)
Аналогичным образом устанавливается связь и с числом
λ
.
