Презентация - Андреев В.К. Механика жидкости и газа
Подождите немного. Документ загружается.


ζ
πζ
ζζ ln
2
)(
*
*
*
i
V
VW
Γ
++=
∞
∞
, (12.2)
где
****
, Γ+=
∞
viuV - скорость на бесконечности и циркуляция скорости по произвольному контуру
*
1
C
,
охватывающему
*
C в плоскости
***
, viuV −=
∞
ζ .
В силу (12.1) )()]([)(
*
ζζ WfWzW == . Продифференцируем по
ζ
обе части этого равенства:
)(
'
*
ζ
ζ
f
dz
dW
d
dW
= ,
или в силу определения комплексного потенциала (11.9)
)(
'*
ζfVV = , (12.3)
а в бесконечно удаленных точках
)(,
'*
∞==
∞∞∞∞
fmVmV . (12.4)
В силу принятого условия направление вектора скорости на бесконечности
∞
V
при конформном
отображении сохраняется, т.е. векторы
*
∞
V и
∞
V параллельны. Отсюда сле
дует параллельность
сопряженных векторов
*
∞
V
и
∞
V
, а из (12.4) получается, что
∞
m - действи
тельная величина, так что
∞∞∞
= VmV
*
, где для определенности
0≥
∞
m
.
Функция )(
ζ
f , осуществляющая конформное отображение, является аналитиче
ской,
следовательно, может быть разложена в ряд Лорана
∑
∞
=
∞
+==
0
)(
n
n
n
m
mfz
ζ
ζζ , (12.5)
сходящийся во всей внешней по отношению к кругу
*
C области 0>ζ .
Коэффициенты главной части этого ряда, представленной суммой членов с отрицат
ельными
степенями
ζ
, можно определить при помощи контурных интегралов ( ,...2,1,0
=
n )
ζζζ
π
df
i
m
n
C
n
1
*
)(
2
1
−
∫
= , (12.6)
вычисленных по окружности
*
C
или по любой другой концентрической окружности, содерж
ащей
внутри себя
*
C .

Преобразующая функция может быть также выражена при помощи интеграла Коши
∫
−
==
*
'
''
)(
2
1
)(
C
df
i
fz
ζζ
ζζ
π
ζ , (12.7)
где
'
ζ - комплексная переменная интегрирования.
Рассмотрим контурный интеграл от сопряженной скорости V по замкнутому контуру C
в
плоскости течения, равный, с одной стороны dzV
C
∫
, а с другой, если перейти в плос
кость комплексного
потенциала ( ψϕ iWV
dz
dW
+== , ),
∫ ∫∫
+==
C CC
diddWdz
dz
dW
),( ψϕ отсюда находим
==−=
Γ==+=
∫∫∫
∫ ∫ ∫
QdvdxudydzVчмчастьмнимая
dvdyudxdzVчдчастььнаядействител
CCC
C C C
ψ
ϕ
)(:.).(
)(:.).(
(12.8)
Γ
- циркуляция скорости по замкнутому контуру C, (
∫ ∫
=∇=Γ
C C
drd ϕϕ ), Q -
расход жидкости через
замкнутый контур C . Рассмотрим теперь циркуляцию
*
Γ
. В силу (12.8) имеем:
Γ====Γ
∫∫∫
dzVчдd
d
dz
VчдdVчд
C
CС
1
*
1
*
1
......
**
ζ
ζ
ζ ,
отсюда следует, что циркуляция скорости по любому замкнутому кон
туру, охватывающему обтекаемый
профиль, при конформном отображении не изменяется.
В результате неизвестные величины
*
∞
V и
*
Γ
выражаются через заданные величины
∞
V
,
Γ
и
коэффициент
∞
m , определяемый согласно (12.4), по известной преобразующей функции
)(
ζ
f
.
Следовательно, окончательно получаем выражение для комплексного потенциала W
в плоскости
течения в виде параметрической зависимости от параметра
ξ

=
Γ
++==
∞
∞∞
).(
,ln
2
)()()(
2
*
ζ
ζ
πζ
ζζ
fz
i
aV
VmWzW
(12.9)
Таким образом,
если известно решение геометрической задачи о конформном отображении
внешней по отношению к обтекаемому контуру C области физической плоскости
z
на внешнюю по
отношению к кругу
*
C произвольного радиуса
a
область вспомогательной плоскости
ζ
, то решение
гидродинамической задачи об определении комплексного потенциала
)(zW
уже не представляет
затруднений.
Из системы (12.9) следует, что задача об обтекании профиля C
потоком заданной по величине и
направле
нию скорости на бесконечности имеет бесчисленное множество решений, зависящих от
произвольного выбора величины циркуляции Г. Как б
ыло показано раньше для случая обтекания
ок
ружности, налагая ту или другую циркуляцию, можно получить бесчисленное множество картин
обтекания кругового цилиндра с различным рас
положением критических точек (рис.11.8). Аналогично
для одного и того же крылового профиля с угловой точ
кой на задней кромке и при той же по величине и
направлению скорости на бесконечности теоретически возможны три типа обтекания (рис.12.2).
В случаях
)a
и
)в
жидкость должна перетекать с одно
й стороны поверхности крыла на другую (в
окрестности задней кромки). При этом на острой кромке должны либо образо
вываться бесконечно
большие скорости, что приводит к физически невозможным бесконечно большим отрицательным
давлениям, либо происходить срывы п
отока с поверхности профиля и вихреобразования. Среди трех
указанных возможных картин течения только одна форма )б с задней критической точкой B
,
совпадающей с угловой точкой на задней кромке профиля, приводит к плавному стеканию стр
уй
жидкости с задней кромки крыла с конечной скоростью.

Н.Е. Жуковский выдвинул следующую гипотезу (постулат)
: среди бесконечного числа
теоретически воз
можных обтеканий профиля с угловой точкой на задней кромке в действительности
осуществляется обтекание с конечной скоростью в этой точке.
Этот постулат получил широкое признание и известен как постулат Жуковского –
Чаплыгина.
Опыт пока
зывает, что существует диапазон углов атаки, при котором профиль обтекается без отрыва
жидкости от его поверхности с плавным сходом с задней кромки.
Крыловые профили, отвечающие постулату Жуковского –
Чаплыгина, называют хорошо
обтекаемыми, остальные – плохо обтекаемыми. Обтекаемость зависит от скорости пото
ка, угла атаки и
других факторов.
Постулат Жуковского – Ч
аплыгина позволяет однозначно определить величину циркуляции Г,
наложение которой приводит к безотрывной форме обтекания крылового про
филя с конечной
скоростью на его задней кромке.
Рис. 12.2

Рис. 12.3
Пусть угловой т.
B
(рис.12.3) на профилеC соответствует некоторая т.
*
B
на окружности круга
*
C
.
Эти точки являются особыми точками преобразования, так как в них нарушается основное свойство
конформного преобразования – сохранение углов между касатель
ными к преобразуемым контурам.
Действительно, внешний угол с вершиной в т. В на задней кромке, равный
δ
π
−
2
, где
δ
-
внутренний
острый угол на задней кромке, переходит в плоскости
ζ
в не равный ему угол
π
с вершиной в т. В
*
.
Рассмотрим конформное отображение внешней по отношению к профилю С
малой области
вблизи вершины угла B на малую, внешнюю по отношению к кругу
*
C область вблизи т.
*
B
в плоскости
ζ
. Это конформное отображение представляется формулой
π
δπ
ζζ
−
−=−
2
)(
*
B
B
Mzz
, (12.10)
где
B
z и
*
B
ζ - комплексные координаты точек
B
и
*
B
в плоскостях
z
и
ζ
, а М -
некоторое
действительное число. В самом деле, положив вблизи точек В и
*
B
*
*
*
,
ββ
ζζ
i
B
i
B
errezz =−=−
и
подставив в (12.10), получим
*
2
2
*
β
π
δπ
π
δπ
β
−
−
=
i
i
eMrre . Отсюда πβ
π
δ
π
β k2
2
*
±
−
= ,
т.е. изменению
*
β
на
π
соответствует изменение
β
на
)2(
δ
π
−
.

Пользуясь преобразующей функцией (12.10), установим связь между скоростями в точках В и В
*
:
****
)()()()(
*
B
B
B
B
BB
d
dz
V
d
dz
dz
dW
d
dW
V
ζζζ
===
,
или, вычисляя производную по (12.10),
π
δπ
ζζ
ζζ
π
δπ
−
=
−
−
=
*
**
)(
2
B
B
B
MVV .
Поскольку
π
δ
<
, то последний сомножитель равен нулю. Отсюда следует (
0
*
=
B
V
), что
соответствующая задней кромке профиля точка во вспомогательной плоскости долж
на быть
критической.
Из этого условия, используя (12.9), найдем циркуляцию Г. Т.к. скорость в т.
*
B
равна нулю, то
0
1
2
)(
*
*
*
*
2
2
*
=
Γ
+−==
∞∞
∞∞=
B
B
B
i
aVm
Vm
d
dW
V
B
ζπ
ζ
ζ
ζζ
.
Полагая ,,
0
*
∞
∞∞
==
θ
ε
ζ
i
i
B
eVVea где
0
ε - полярный угол т.
*
B
на окружности
*
C ,
∞
θ -
угол,
образованный скоростью на бесконечности с осями Ox или ξ
*
O , получим
,0
2
00
)2(
=
Γ
+−
−−
∞∞
−
∞∞
∞∞
εεθθ
π
iii
e
ia
eVmeVm
откуда находим
00
()()
4,
2
ii
ee
amV
i
θεθε
π
∞∞
−−−
∞∞
−
Γ=−
или, переходя от показательных функций к тригонометрическим:
).sin(4
0 ∞∞∞
−=Γ θεπ Vma (12.11)

Как видно, вся трудность в решении задачи о безотрывном обтекании
контура поступательным
потоком сводится к отысканию конформного отображения внешности контура С на внешность круга.
Лекция 15
.
Функция Жуковского
Рассмотрим пример конформного отображения
внешности круга во вспомогательной плоскости
на внешность эллипса (в частном случае на внешность отрезка). Это ото
бражение описывается так
называемой функцией Жуковского
).(
2
1
2
ζ
ζ
C
z += (12.12)
Это преобразование является частным случаем общего преобразования (12.5), в котором значения
коэффициентов равны
1
,
2
m
∞
=
2
1
1
,
2
mC
=
23
0.
mmm
===
Окружность
*
C радиуса
c
в плоскости
ζ
называют основной окружно
стью, она преобразуется в
плоскости
z
в отрезок
F
F
'
(рис. 12.4) на оси Ox с концами в точках (-С, 0) и (+С
, 0). В самом деле,
полагая
ε
ζ
i
Ce= , находим
,cos)(
2
ε
εε
⋅=+=
−
Cee
C
z
ii
(12.13)
так что полному обходу окружности )20(
π
ε
≤
≤
соответствует двойной обход отрезка
F
F
'
:
справа
налево по верхней части разреза
F
F
'
и слева направо - по нижней.
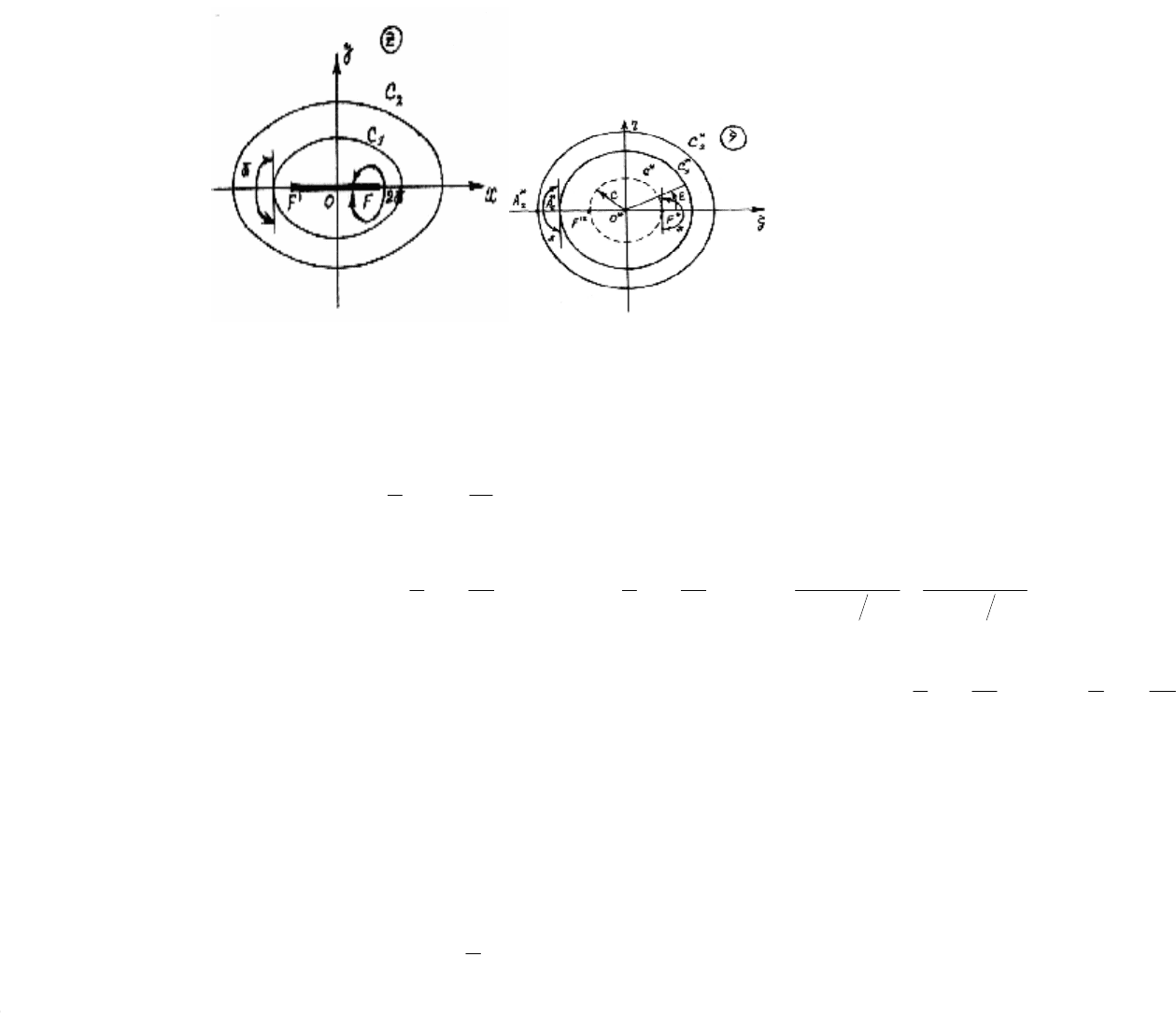
Окружности ,...,
*
2
*
1
CC , концентрические с основной окружностью
*
C , преобра
зуются в софокусные
эллипсы ,...,
21
CC с фокусами
'
,FF .
Действительно, обозначая через
r
радиус какой–
нибудь из окружностей и полагая в (12.12)
)( crre
i
>=
ε
ζ , получим )(
2
1
2
εε ii
e
r
c
rez
−
+= , откуда следует
1
)(
4
)(
4
,sin)(
2
1
,cos)(
2
1
22
2
22
222
=
−
+
+
−=+=
rcr
y
rcr
x
r
c
ry
r
c
rx εε
.
Обозначим полуоси эллипсов через
a
и b , тогда из равенств
),(
2
1
2
r
c
ra +=
)(
2
1
2
r
c
rb −=
следует
222
, cbabar =−+=
, т.е. все рассматри
ваемые эллипсы имеют общее фокусное расстояние 2С и фокусы
в точках
F
и
'
F
.
Комплексный потенциал )(zW обтекания любого из эллипсов (в физической плоскости) ,,
21
CC
в
том числе в пределе и отрезка
F
F
'
, со скоростью на бесконечности
∞
V , образующей с осью Ox угол
∞
θ
,
и циркуляцией Г составим в параметрической форме (12.9)
,
ln
)
(
1
)
(
ζ
ζ
ζ
b
a
V
V
W
Γ
+
+
+
=
∞
(12.14)

в случае обтекания отрезка
F
F
'
надо положить
.,0 acb ==
Исключим в (12.14) комплексный параметр
ζ
. Из второго соотношения находим
,
22
czz −±=ζ (12.15)
причем перед корнем взят верхний знак, что соответствует отображе
нию внешности эллипса на
внешность круга. В самом деле, принимая нижний знак, получим
22
2
22
czz
c
czz
−+
=−−=ζ
и 0
=
ζ
при
∞
=
z
,
т.е. внешности эллипса соответствовала бы внутренность круга.
Таким образом, получаем явное выражение комплексного потенциала обтекания эллипса
)ln(
2
)(
(
2
1
)(
22
22
2
22
czz
i
czz
baV
czzVzW −+
Γ
+
−+
+
+−+=
∞
∞
π
или
)ln(
2
)(
)(
2
1
)(
2
1
)(
2222
2
2
22
czz
i
czzV
c
ba
czzVzW −+
Γ
+−−
+
+−+=
∞∞
π
(12.16)
Обтекание эллипса при Г=0 показано на рис. 12.5. Нулевая линия ток
а проходит через
критические точки А и В, положения которых зависят от угла атаки
∞
θ . Полагая в (12.16) abc == ,0
,
получим комплексный потенциал циркуляционного обтекания круга.

Рис. 12.5
Так как
z
c
czz
c
2
1
0
2
22
=
−−
=
, то z
iz
aV
zVzW ln
2
)(
2
π
Γ
++=
∞
∞
.
Полагая в (12.16) cab == ,0 , можно найти комплексный потенциал циркуляци
онного обтекания
пластинки длины 2с (отрезка
'
FF
)
),ln(
2
)ln(
2
)(
2
1
)(
2
1
)(
2222
2222
czz
i
czivzu
czz
i
czVVzVVzW
−+
Γ
+−−=
=−+
Γ
+−−−+=
∞∞
∞∞∞∞
π
π
(12.17)
где
∞∞
vu , - проекции скорости
∞
V .
На рис. 12.6 показана картина линий тока обтекания пластинки при Г=0.
Нулевая линия тока
состоит из по
верхности пластинки и двух отрезков софокусной гиперболы, параметры которой зависят
от угла атаки
∞
θ .
