Презентация - Андреев В.К. Механика жидкости и газа
Подождите немного. Документ загружается.

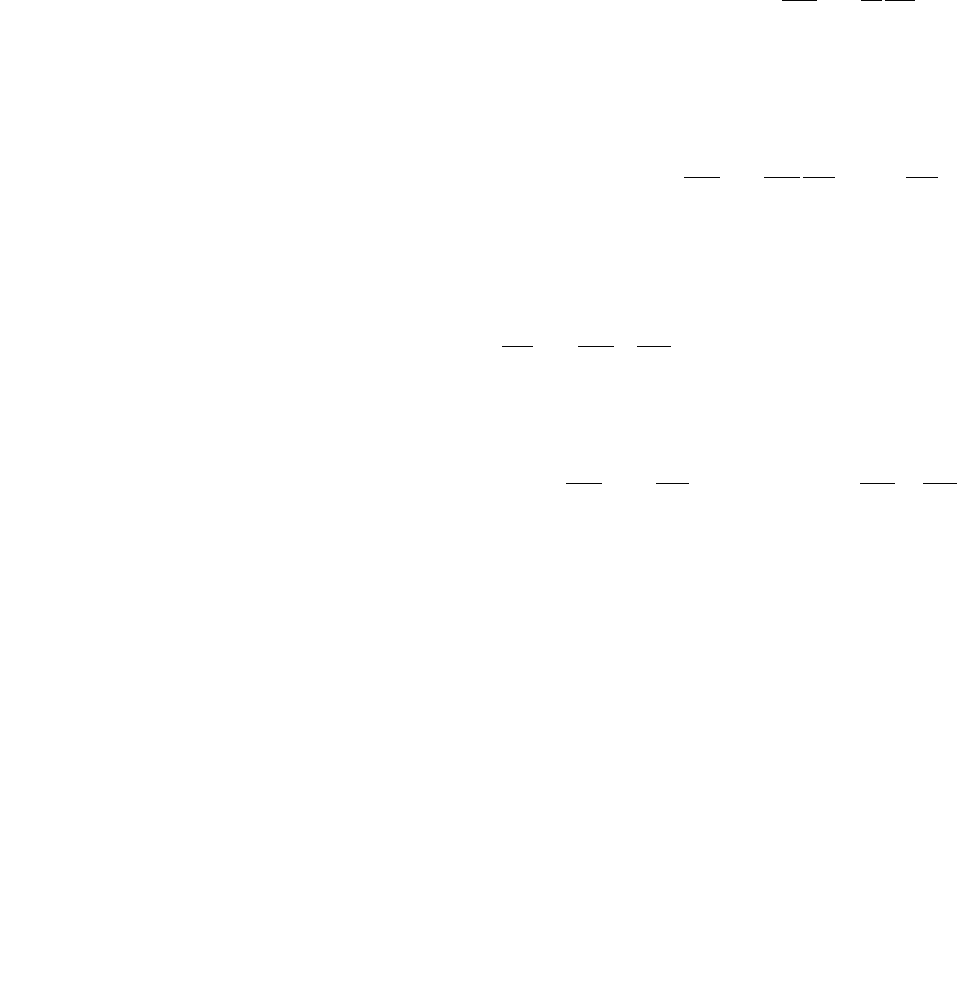
Рассмотрим течение газа по трубе переменного сечения.
Из уравнения движения (уравнение Эйлера)
dx
dp
dx
dV
V
ρ
1
−=
и уравнения неразрывности (3.13)
const
VF
ρ
=
(F – площадь поперечного сечения трубы).
Найдем связь между изменениями скорости и площади сечения трубы:
ρ
ρ
ρ
ρ
ρρ
d
a
d
d
pdpd
VdV
2
−=−=−= .
Возьмем дифференциал от соотношения (13.13)
0
=
+
+
VdFFdVVFd
ρ
ρ
ρ
или
F
dF
V
dVd
−−=
ρ
ρ
.
Тогда из предыдущего уравнения, исключая плотность, находим
F
dF
a
V
dV
aV
222
)( =− или
F
dF
V
dV
M =− )1(
2
. (13.26)
Из полученного уравнения, носящего имя Гюгонию, вытекают следствия:
Если М <1, знак dV противоположен знаку dF
, т.е. при дозвуковом движении газа, так же как и
для несжимаемой жидкости, с возрастанием площади сечения трубы скорость движения уменьшается и
,
наоборот, при уменьшении сечения скорость увеличивается.
Если М >1, знак dV одинаков со знаком dF
, т.е. при сверхзвуковом движении газа в сужающейся
трубе движение замедляется, в расширяющейся трубе – ускоряется.
Если М =1, то
dF
=0; соответствующее сечение трубы будет критическим. Условие
dF
=0 совпадает с необходимым
условием экстремума пл
ощади сечения. Очевидно, что критическое сечение будет минимальным (т.к.
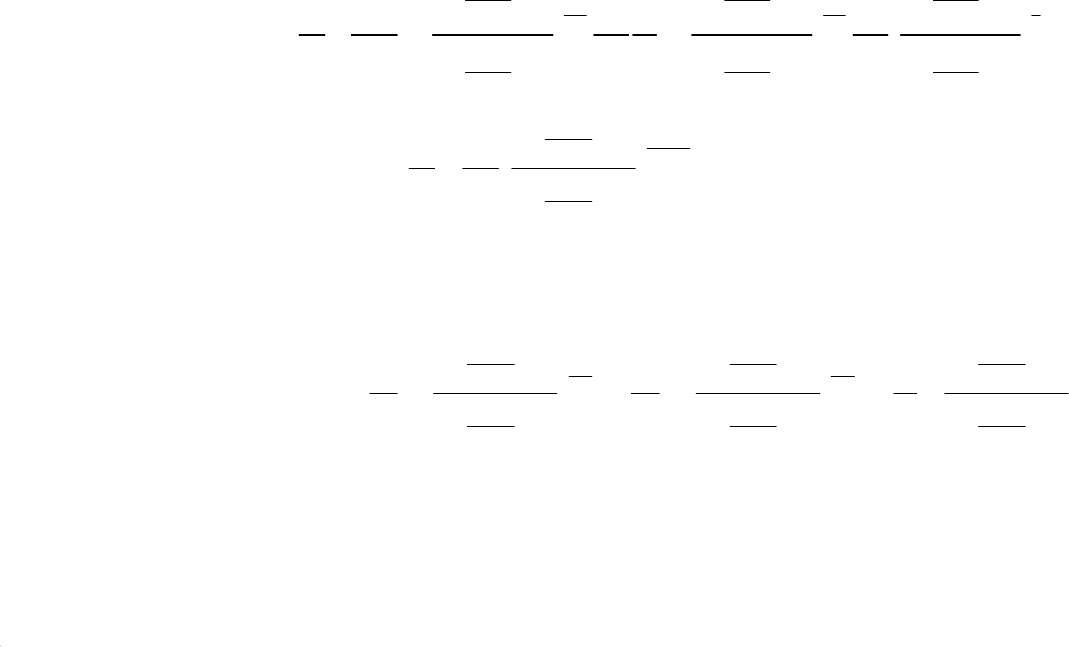
при подходе к максимальному сечению дозвуковой поток замедляется, а сверхзвуковой
-
ускоряется, что не может привести к течению со скоростью звука в критическом сечении).
Если
dF
=0 и сечение экстремально (максимально или минимально), то либо М
=1 и,
следовательно, это сечение критическое, либо
1
≠
M
и dV
=0. В последнем случае каково бы ни было
движение – дозвуковое или сверхзвуковое, скорость в экстремальном сечении
принимает также
экстремальное значение: при дозвуковом течении газа – мини
мальное в максимальном сечении и
максимальное в минимальном сечении, при сверхзвуковом течении, наоборот, в максимальном сечении
скорость максимальна, в минимальном минимальна.
Испо
льзуя уравнение неразрывности (13.13) и (13.24), найдем связь между параметрами
одномерного потока и площадью сечения, заданной функцией от координаты
x
(индекс “1” относится к
какому-нибудь фиксированному сечению трубы):
.)
2
1
1
2
1
1
()
2
1
1
2
1
1
()
2
1
1
2
1
1
(
2
1
2
1
2
1
1
1
2
1
2
11
1
1
2
1
2
11
1
M
k
M
k
M
M
M
k
M
k
a
a
M
M
M
k
M
k
V
V
F
F
kk
−
+
−
+
−
+
−
+
=
−
+
−
+
==
−−
ρ
ρ
.)
2
1
1
2
1
1
(
)1(2
1
2
1
2
1
1
−
+
−
+
−
+
=
k
k
M
k
M
k
M
M
F
F
(13.27)
Это соотношение совместно с изоэнтропическими формулами
2
2
1
1
1
1
2
2
1
1
1
2
2
1
1
2
1
1
2
1
1
,)
2
1
1
2
1
1
(,)
2
1
1
2
1
1
(
M
k
M
k
T
T
M
k
M
k
M
k
M
k
p
p
kk
k
−
+
−
+
=
−
+
−
+
=
−
+
−
+
=
−−
ρ
ρ
(13.28)
дае
т параметрическое решение задачи об одномерном газовом потоке в трубе переменного сечения
(роль параметра играет число М). По заданному закону изменения площади сечения )(xF
из (13.27)
определяется )(xM , а затем из (13.28) - искомые функции ),(xp ),(x
ρ
),(xT ).(xV

Лекция 18.
Прямой скачок уплотнения (
VVD
nn
== ,0
)
В этом случае условия (3.12) примут вид:
=
=
−
=
+=+
+=+
=
.
,,
1
,
2
1
2
1
,
,
2
2
1
2
1
2
1
2
11
11
RTp
kp
a
p
k
k
h
hVhV
pVpV
VV
ρ
ρρ
ρρ
ρρ
(3.29)
Отсюда можно получить формулы, выражающие отношение плотностей, давлений и температур
на ударной волне через число Маха :
1
1
1
a
V
M =
[ ][ ]
.
)1(
2)1()1(2
;
1
1
1
2
;
)1
1
1
2
(
1
)1(
)1(
2)1(
)1(
2
1
2
2
1
2
1
1
2
1
1
2
1
2
1
2
1
11
Mk
MkkkM
T
T
k
k
M
k
k
p
p
M
k
k
k
Mk
Mk
V
V
+
+−−−
=
+
−
−
+
=
+
−
−
+
=
+−
+
==
ρ
ρ
(13.30)
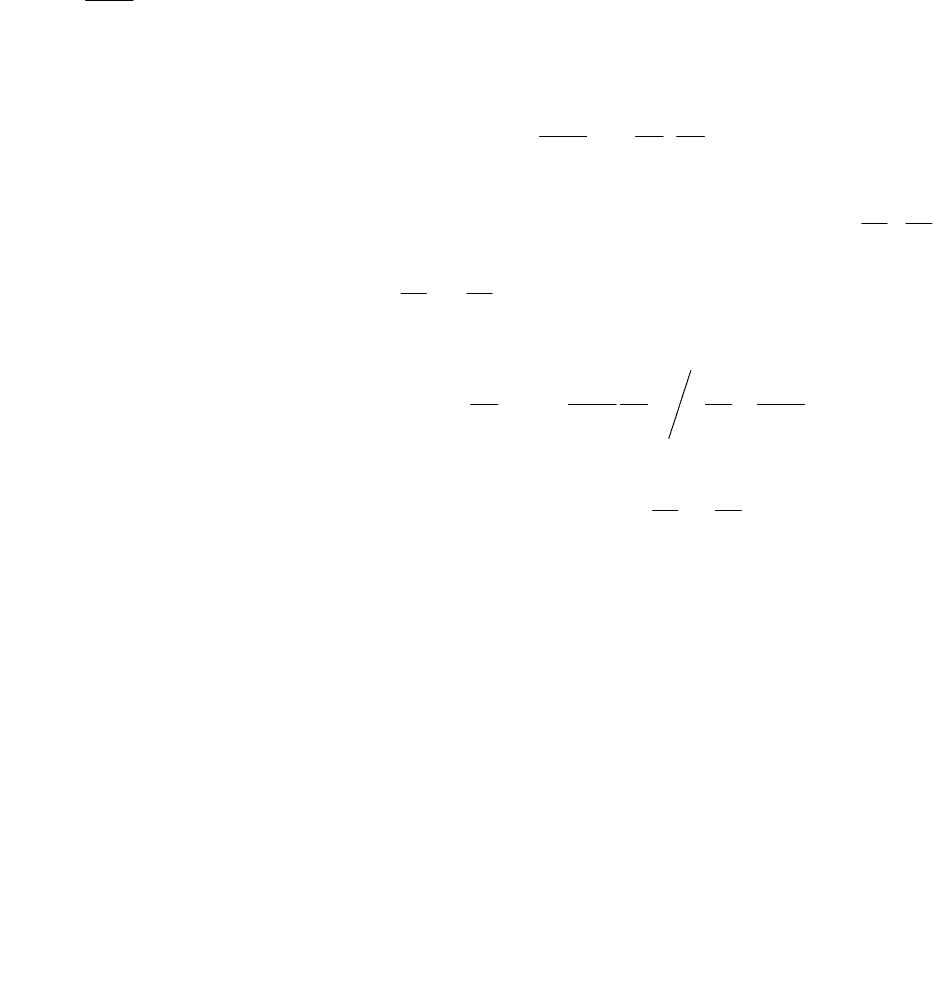
Из приведенных формул следует, что интенсивность скачков увеличивается с ростом скорости
невозмущенного потока (
1
M ). Отношение плотностей при ∞→
1
M
стремится к конечному пределу
1
1
−
+
k
k
, а отношения давлений и температур возрастают неограниченно. Для воздуха ( 4.1
=
k
) плотность за
скачком уплотнения не может увеличиться более чем в шесть раз.
Изменение энтропии определяется уравнением
−
=∆=−
k
p
p
k
R
SSS )(ln
1
1
1
1
ρ
ρ
.
Для изоэнтропических процессов (обратимых) 0
=
∆
S и
1))((
1
1
=
k
p
p
ρ
ρ
. Исключив
2
1
M
из
соотношений (13.30) для
1
p
p
и
1
ρ
ρ
, получим:
−
+
−
−
+
−=
1
1
1
1
1
111
k
k
k
k
p
p
ρ
ρ
ρ
ρ
- ударная адиабата.
Для скачка уплотнения )(
1
ρρ > всегда
k
p
p
)(
11
ρ
ρ
> и, следовательно, 0
>
∆
S
, т.е. при переходе через
скачок энтропия газа возрастает. Увеличени
е энтропии в скачке объясняется необратимым характером
изменения состояния газа в скачке. В результате такого
процесса часть кинетической энергии газа
необратимо переходит в теплоту, т.е. внутренняя энергия потока необратимо возрастает.
§14. Движение вязкой жидкости. Слоистые течения в каналах и круглых трубах
Уравнения Навье-Стокса описывают движение реальной вязкой жид
кости, характер движения
которой наиболее заметно меняется вблизи обтекаемых твердых поверхно
стей. На твердых стенках,
находящихся в покое, выполняется условие нулевой скорости жидкости (гипотеза «прилипания»).
Одним из наиболее простых случаев движения вязкой несжимаемой жидкости является так
называемое ла
минарное (слоистое) движение по цилиндрической трубе произвольного сечения (или в
канале, ограниченном двумя параллельными плоскими стенками), при котором линии тока – пря
мые
линии, параллельные оси трубы (плоским стенкам).
Как показывают опыты, такое движение реализуется, если только число Рейнольдса (
ν
00
Re
LV
=
,
где
0
V
- характерная скорость течения,
0
L
- масштаб длины (диаметр трубы),
v
-
кинематический
коэффициент вязкости)
не превосходит некоторого определенного критического значения, после чего
движение перестает быть ламинарным, частицы жидкости приобретают сложные траектории.
Итак, рассмотрим слоистые течения несжимаемой вязкой жидкости. Уравнения Навье – Стокса:
.0
,
1
)(
=
∆+∇−=∇+
∂
∂
Vdiv
VpVV
t
V
ν
ρ
(14.1)
Плоскопараллельное течение в канале, ограниченном параллельными плоскими стенками
.
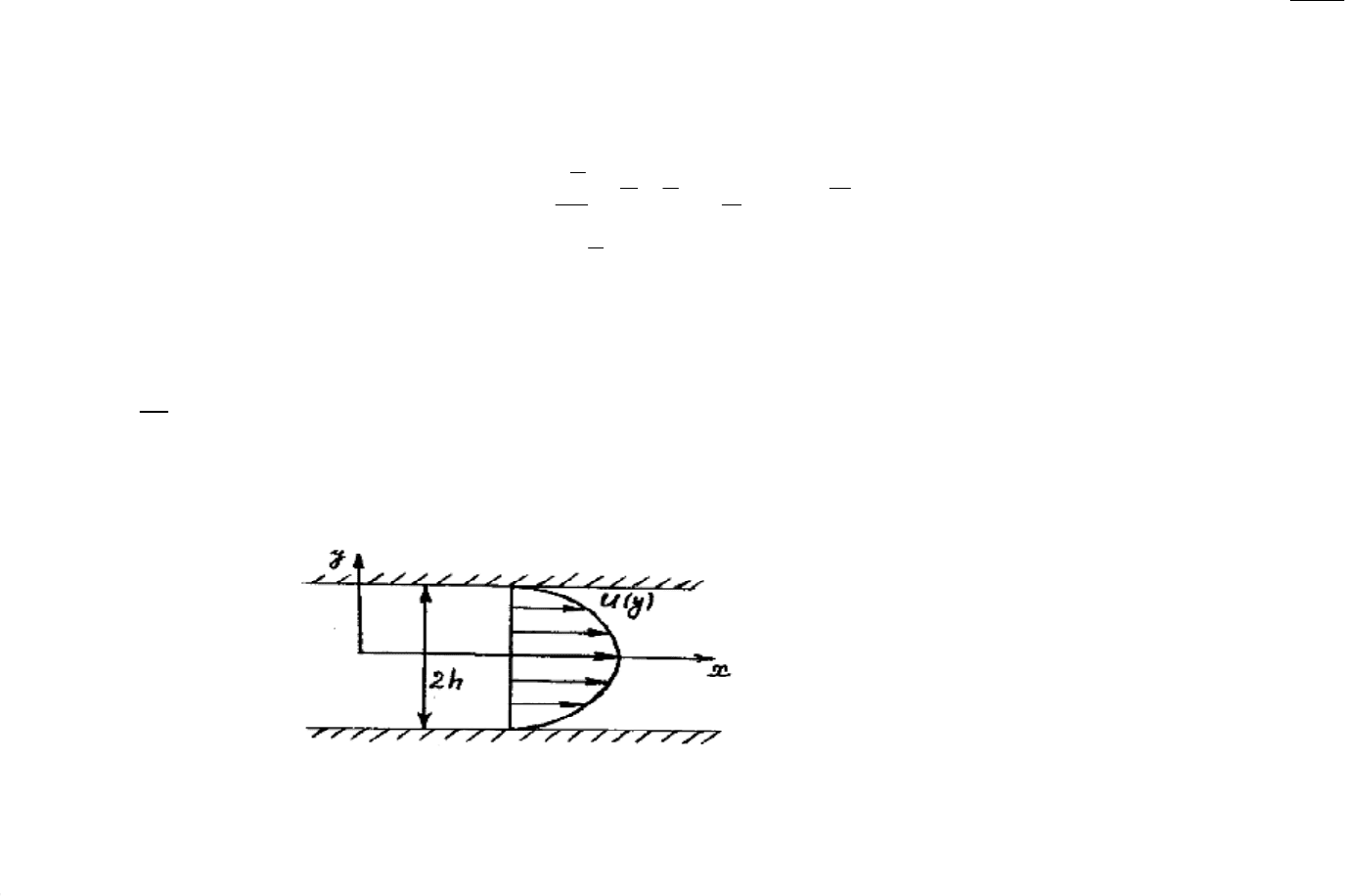
Рассматриваем установившиеся течения. Для слоистых течений имеется только одна составляющая
скорости
u
(рис. 14.1), а составляющие
v
и
w
равны нулю. Тогда из уравнени
я неразрывности следует,
что
0
u
x
∂
=
∂
. Т.е. для слоистых течений ),( zyuu
=
, в плоском случае )(yuu
=
. Из уравнений (14.1)
получаем
Рис. 14.1
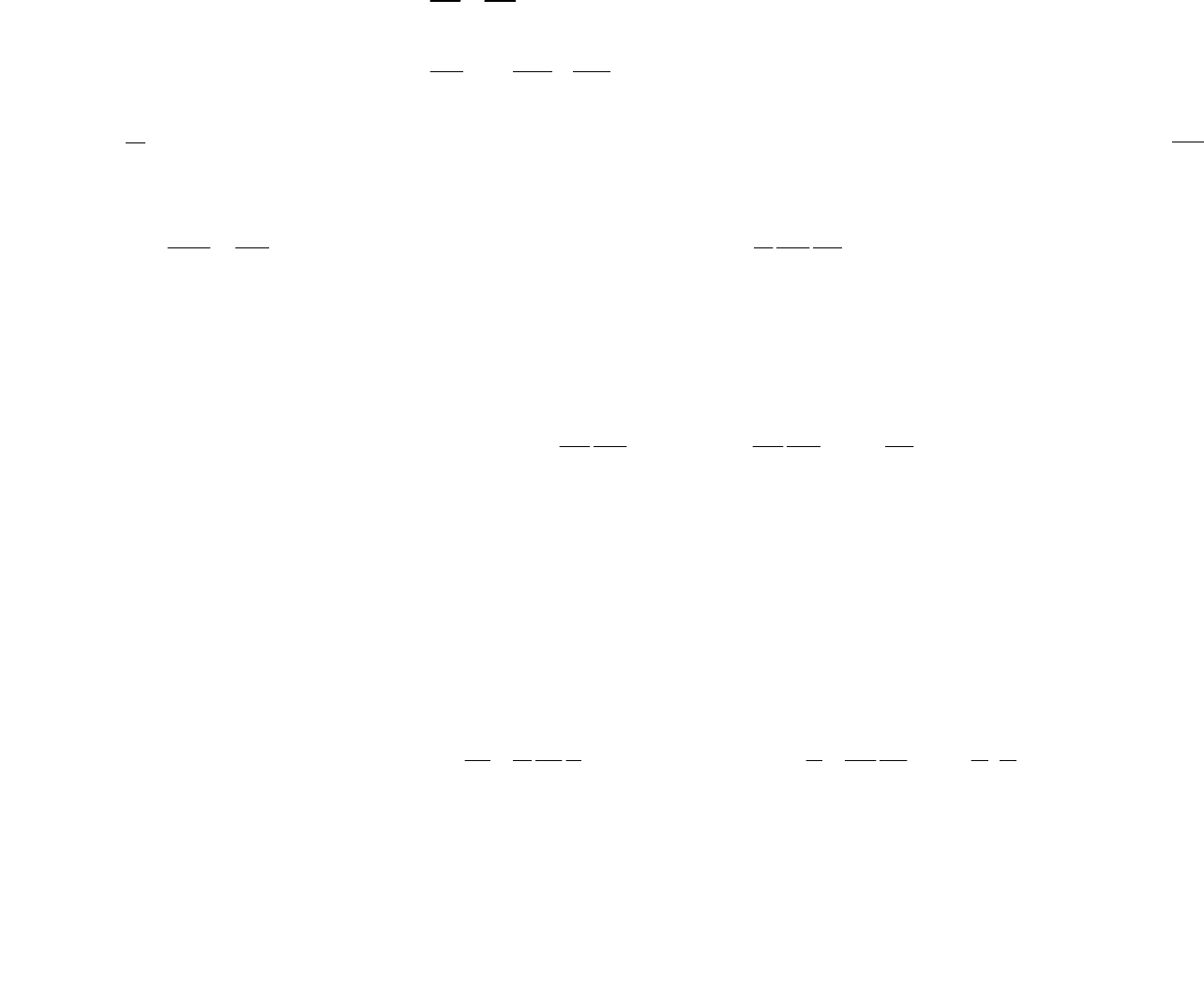
22
22
0,
().
pp
yz
dpuu
dxyz
µ
∂∂
==
∂∂
∂∂
=+
∂∂
(14.2)
)(
ρ
µ
ν=. Слева в уравнении (14.2) стоит функция координат
y
и
z
, равенство возможно, если
const
dp
dx
=
.
В плоском случае
u
зависит только от
y
и уравнение (14.2) примет вид
,
2
2
xd
pd
yd
ud
=µ решение этого уравнения имеет вид ,
2
1
21
2
cyc
y
xd
pd
u ++=
µ
где
21
, cc - произвольные постоянные, для определения которых имеются два условия:
)0;)0
ayhu б yhu===−=
(h - расстояние от оси канала до соответствующей стенки).
В результате:
2
21
2
1
,0 h
xd
pd
cc
µ
−== и
).1(
2
1
2
2
2
h
y
h
xd
pd
u −−=
µ
(14.3)
Течение, которое образуется между двумя параллельными пластинами, одна из которых движется
с постоянной скоростью
0
u , называется течением Куэтта. В этом cлучае граничные условия имеют вид:
0
);00) uubyбuya ====
(в данном случае начало координат располагается на нижней неподвижной плоскости, b -
расстояние
между пластинами).
.)1(
2
1
,0,
2
1
2
02
0
1
b
y
b
y
b
dx
dp
b
y
uuc
b
dx
dp
b
u
c −−==−=
µµ
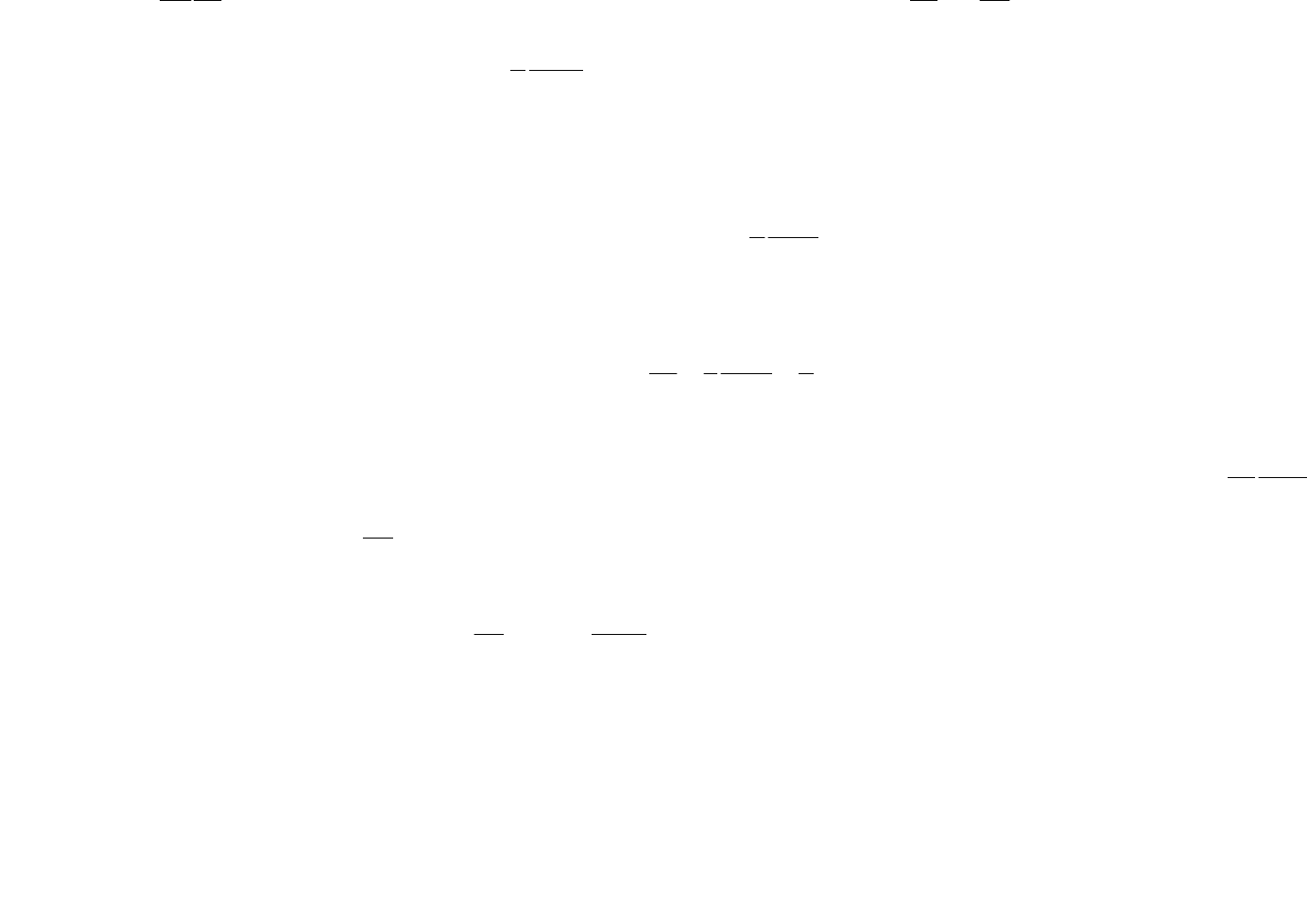
Распределение скоростей (14.3) представляет собой параболу.
Максимальная скорость
max
u достигается в плоскости симметрии потока )0(
=
y
и равна
2
max
2
1
h
dx
dp
u
µ
−= , или, с введением обозначения для падения давления,
l
p
dx
dp
∆
−= (
p
∆
-
падение давления
на участке длины l ), получим .
.2
1
2
max
µl
ph
u
∆
=
Найдем объемный расход жидкости, отнесенный к единице ширины в направлении Oz
,
перпендикулярном плоскости, параллельно которой происходит движение:
.
3
2
3
µl
ph
udyQ
h
h
∆
==
∫
−
Определим среднюю по сечению скорость:
max
2
3
2
3
1
2
u
l
ph
h
Q
u
ср
=
∆
==
µ
.
Введем коэффициент сопротивления
ζ
движению жидкости при помощи формулы
2
22
cp
u
l
p
h
ρ
ζ∆=
и, учитывая выражение
l
p
∆
через
cp
u , получим закон сопротивления для плоской трубы:
.
2
Re,
Re
24
ν
ζ
hu
cp
==
(14.4)

Лекция 19
.
Слоистое движение несжимаемой жидкости в трубах
Рассмотрим течение сквозь цилиндрическую трубу эллиптического сечения. Пу
сть сечение трубы
есть эллипс с полуосями
a
и b , уравнение которого в плоскости
Oyz
имеет вид
,1
2
2
2
2
=+
b
z
a
y
то
гда
решение уравнения (14.2), удовлетворяющее граничному условию обращен
ия скорости в нуль на
контуре сечения, будет
),1(
2
2
2
2
b
z
a
y
Au −−=
(14.5)
где согласно уравнению (14.2) постоянная А определяется из соотношения
22
111
2()
dp
A
abdx
µ
−+= .
Введем обозначение
const,
dpp
dxl
∆
==−
где
p
∆
- постоянное вдоль трубы падение давления на произвольно выбранном участке длины
l.
Перепад давле
ния либо задается, либо выражается через другие заданные величины (расход жидкости
через трубу, среднюю по сечению скорость).
Итак, для определения А имеем
22
22
2 ba
ba
l
p
A
+
∆
=
µ
.
Распределение скоростей в сечении эллиптической трубы описывается формулой
)1(
2
2
2
2
2
22
22
b
z
a
y
ba
ba
l
p
u −−
+
∆
=
µ
(14.6)’
или
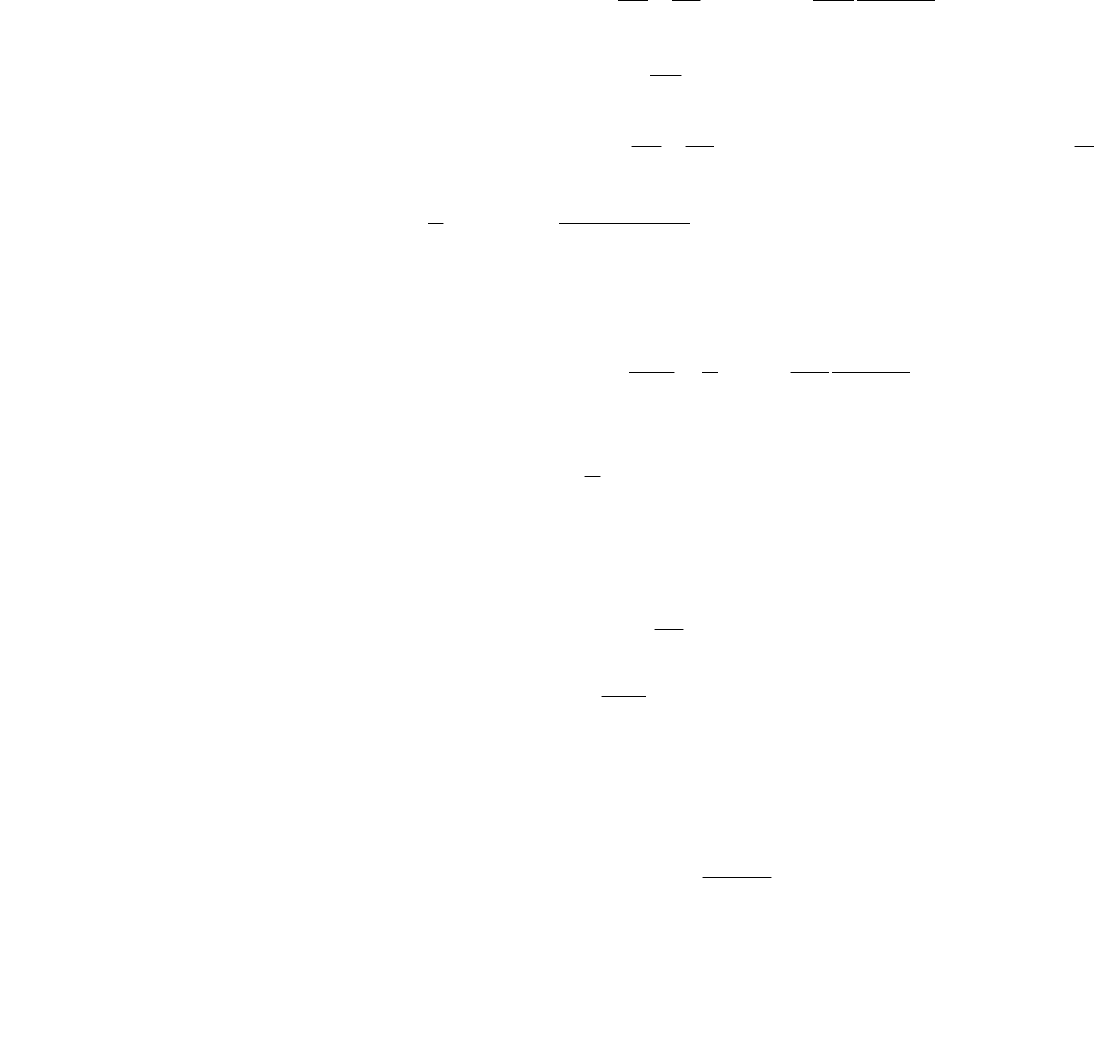
22
22
max
2
2
2
2
max
2
),1(
ba
ba
l
p
u
b
z
a
y
uu
+
∆
=−−=
µ
. (14.6)
Найдем объемный расход жидкости Q )(
3
с
м
через сечение эллиптической трубы:
,
2
2)1()1(
max
1
0
''2'
max
2
2
2
2
max
ubadrrrbaudzdy
b
z
a
y
udzdyuQ
SS
π
π =−⋅=−−==
∫∫∫∫∫
.
)(4
2
1
22
33
max
bal
pba
ubaQ
+
∆
==
µ
π
π
(14.7)
Среднюю скорость
cp
u определим как отношение расхода Q к площади сечения трубы baS
π
=
:
22
22
max
42
1
ba
ba
l
p
u
ba
Q
u
cp
+
∆
===
µπ
. (14.8)
В отличие от плоской трубы в эллиптич
еской трубе средняя скорость равна половине
максимальной (в плоскоской трубе
max
3
2
uu
cp
= ).
Для цилиндрической трубы круглого сечения ( aba ,= - радиус трубы) имеем
).(
,2
4
),1(
222
max
2
2
max
zyr
u
l
pa
u
a
r
uu
cp
+=
=
∆
=
−=
µ
(14.9)
Объемный расход по (14.8) равен
µl
pa
Q
8
4
4
∆
= . (14.10)
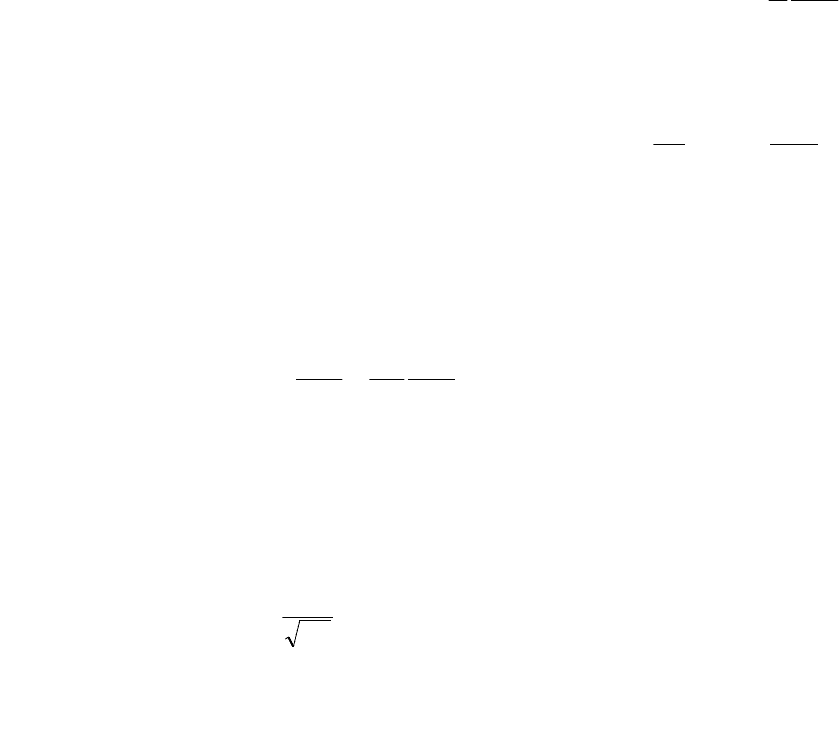
Получили известный закон Пуазейля: при установившемся ламинарном движении вязкой
несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объемный расход
пропорционален перепаду давления на единицу длины трубы и четвертой степени ее радиуса.
Из формулы (14.10) следует, что для получения заданного расхода че
рез трубы разного радиуса
перепад давления обратно пропорционален четвертой степени радиуса трубы. Это свойство имеет
важное значение в задачах п
рогонки жидкостей сквозь трубы малого диаметра, а также в случаях
движения очень вязких жидкостей.
Определим коэффициент сопротивления
ξ
для круглой трубы:
2
2
ρ
ζ
cp
u
d
l
p =∆ ,
выражая p
∆
через
cp
u по (14.9), получим закон сопротивления для цилиндрических круглых труб:
ν
ζ
du
cp
== Re,
Re
64
. (14.11)
Это соотношение отражает закон Пуазейля для движения жидкости в трубах.
Следует помнить,
что этот закон имеет место для сложных (ламинарных) течений.
§15. Основные понятия о пограничном слое
При изучении теории ламинарных течений в трубах считалось, что числа Рейнольдса малы. Число
Рейнольдса
0
2
2
00
Re
U
L
L
ULU
νν
== характеризует отношение сил инерции к силам вязкости. При
∞
→
Re
уравнения Навье-
Стокса переходят в уравнения Эйлера для невязких жидкостей. Порядок уравнений
Эйлера ниже, чем уравнений Навье-
Стокса. Поэтому решения уравнений Эйлера нельзя подчинить
граничному условию равенства нулю как нормальной, так и касате
льной составляющих скорости на
поверхности обтекаемого тела (условия прили
пания). Поэтому уравнения Эйлера непригодны для
описания течений вблизи поверхности тела. Порядок толщи
ны слоя, в котором необходимо учитывать
вязкость, равен
Re
1
(будет показано ниже).
Эта внутренняя область течения вязкой жидкости называется пограничным слоем.
