Презентация - Андреев В.К. Механика жидкости и газа
Подождите немного. Документ загружается.

Уравнения Навье – Стокса
Используя обобщенный закон Ньютона для тензора напряжений, из уравнений сохранения
количества движения (5.12) получаются уравнения (для
const
µ
=
)
( )
.
1
VpgVV
t
V
∆+∇−=∇⋅+
∂
∂
ρ
µ
ρ
(7.6)
Здесь учли зависимости
.;
∂
∂
+
∂
∂
=+−=
i
j
j
i
ijijijij
x
V
x
V
pp µττδ (7.7)
∆
- оператор Лапласа. Уравнения (7.6) называются уравнениями Навье – Стокса.
Если к системе уравнений (7.6) добавить уравнение неразрывности
,0=Vdiv (7.8)
то получим систему из четырех скалярных уравнений для нахождения четырех функций .,,,
321
pVVV
Таким образом, выписанная система замкнута.
Сформулированная математическая модель описывает слоистые упорядоченны
е течения
жидкости, которые называются ламинарными.
Для решения конкретных прикладных задач необходимо задать начальные и гра
ничные условия.
В качестве начальных условий задается поле скоростей в изучаемой области. Граничные условия
включают: условия прилипания на (неподвижных) твердых стенках: ;0| =
Γ
V
на свободной поверхности
ставятся кинематические и динамические условия.
Диссипация энергии в несжимаемой жидкости
Наличие вязкости приводит к диссипации энергии, переходящей в тепло. Вычислим
диссипируемую
энергию несжимаемой жидкости. Полная кинетическая энергия несжимаемой жидкости равна
.
2
2
∫
Ω= dVE
кин
ρ
Найдем производную от этой энергии по времени.

.)(
1
)6.7(,0
,
2
2
VVpVVVVV
x
p
x
V
VV
получаемсилувgполагаемдалее
еианвсуммиросятеавподразумеiиндексупоздесь
t
V
V
V
t
i
ik
i
ki
i
i
∆⋅+∇⋅−∇⋅−=
∆+
∂
∂
−
∂
∂
−⋅⋅=
=
=
=
∂
∂
⋅⋅=
∂
∂
µρ
ρ
µ
ρ
ρ
ρ
ρ
(7.9)
Так как имеет место тождество
(
)
,aVVdivaVadiv ∇⋅+≡
то для несжимаемой жидкости
( ) ( ) ( ) ( )
2
0,,
2
i
iiii
V
divVVpdivpVVVVVdivVVdivV
=⋅∇=⋅∇==
(),()(),
iiiiii
divVdivVdivVVVV
∆=∇∇=∇−∇⋅∇
из (7.9) следует
( )
.
22
22
iiii
VVVV
pV
Vdiv
V
t
∇⋅∇−
∇−
+−=
∂
∂
µµ
ρ
ρ
ρ
(7.10)
Проинтегрируем соотношение (7.10) по некоторому объему
Ω
, используя формулу Гаусса
–
Остроградского
(
)
,dГVdVdiv
ii
αϕϕ
∫∫
ΓΩ
⋅=Ω где
i
α - направляющие косинусы нормали к поверхности Г,
.
22
22
Ω∇⋅∇−Γ
∇⋅−
+−=Ω
∂
∂
=
∂
∂
∫∫∫
ΩΓΩ
dVVdVV
pV
Vd
V
tt
E
ii
кин
µµ
ρ
ρ
ρ
(7.11)
Первый член справа определяет изменение кинетической энергии жидкости в объеме
Ω
вследствие потока энергии че
рез поверхность этого объема. Второй член представляет собой
уменьшение кинетической энергии в единицу времени, обусловленное диссипацией.
Если распространить интегрирование по всему объему жидкости, то интеграл по поверхности
исчезает. Таким образом, получаем окончатель
ную формулу для диссипации энергии в несжимаемой
жидкости:
.
∫
Ω
Ω∇⋅∇−=
∂
∂
dVV
t
E
ii
кин
µ (7.12)
Так как подынтегральное выражение положительное, то диссипация приводит к уменьше
нию
механической энергии.

Лекция 8.
§8. Движение идеальной жидкости. Интеграл Бернулли
Рассмотрим течения идеальной невязкой жидкости. Преобразуем уравнения количества движения.
Воспользуемся известной формулой векторного анализа
(
)
(
)
(
)
.brotaarotbbaabba ×+×+∇+∇≡⋅∇
Положив в ней Vba == , получим
( )
.
2
2
∇+×=∇⋅
V
VVrotVV
Тогда уравнения движения для невязкой жидкости принимают вид
.
1
2
2
pgVVrot
V
t
V
∇−=×+
∇+
∂
∂
ρ
(8.1)
Эта форма уравнения называется уравнением Громеко – Лэмба.
Рассмотрим вначале случай стационарного течения (т.е. 0=
∂
∂
t
V
). Умножим скалярно ур
авнение
(8.1) на вектор V . Тогда получим
.0
1
2
2
=
−∇+
∇⋅ gp
V
V
ρ
(8.2)
Предположим, что массовые силы
g
имеют потенциал П, такой, что
,
Π
−∇
=
g
(8.3)
а также плотность зависит только от давления, т.е. существует функция
.
)(
)(
0
∫
=Ρ
p
p
p
dp
p
ρ
(8.4)
Течения, в которых плотность зависит только от давления, называются баротропными.

Из (8.4) следует
.
1
)( pp ∇=Ρ∇
ρ
Функцию )( p
Ρ
можно рассматривать как потенциал объемного действия поверх
ностных сил.
Итак, из (8.2) получаем
,0
22
22
=
Π+Ρ+=
Π+Ρ+∇⋅
V
ds
dV
V
где
ds
d
означает производную вдоль линии тока. Отсюда следует, что
2
const.
2
V
+Ρ+Π=
(8.5)
Это соотношение справедливо вдоль линии тока (или траектории). При пере
ходе от одной линии тока к
другой константа, вообще говоря, изменя
ется. Равенство (8.5) в силу (8.1) будет справедливо в
области течения, если ,0=×VVrot что возможно при 0=Vrot (безвихревое течение) или
.VVrot
Равенство (8.5) носит название интеграла Бернулли
(или уравнения Бернулли). Для несжимаемой
жидкости
const.
ρ
=
Тогда
const.
p
ρ
Ρ=+
Если жидкость находится только под действием сил тяжести, то
const,
gz
Π=+
где z
–
вертикальная ось, направленная вверх, g – ускорение силы тяжести. В этом случае урав
нение Бернулли
принимает следующий вид:
2
const.
2
Vp
gz
ρ
++=
(8.6)
Поделим все члены на ускорение g и обозначим константу через H, то получим
,
2
2
Hz
p
g
V
=++
γ
(8.7)
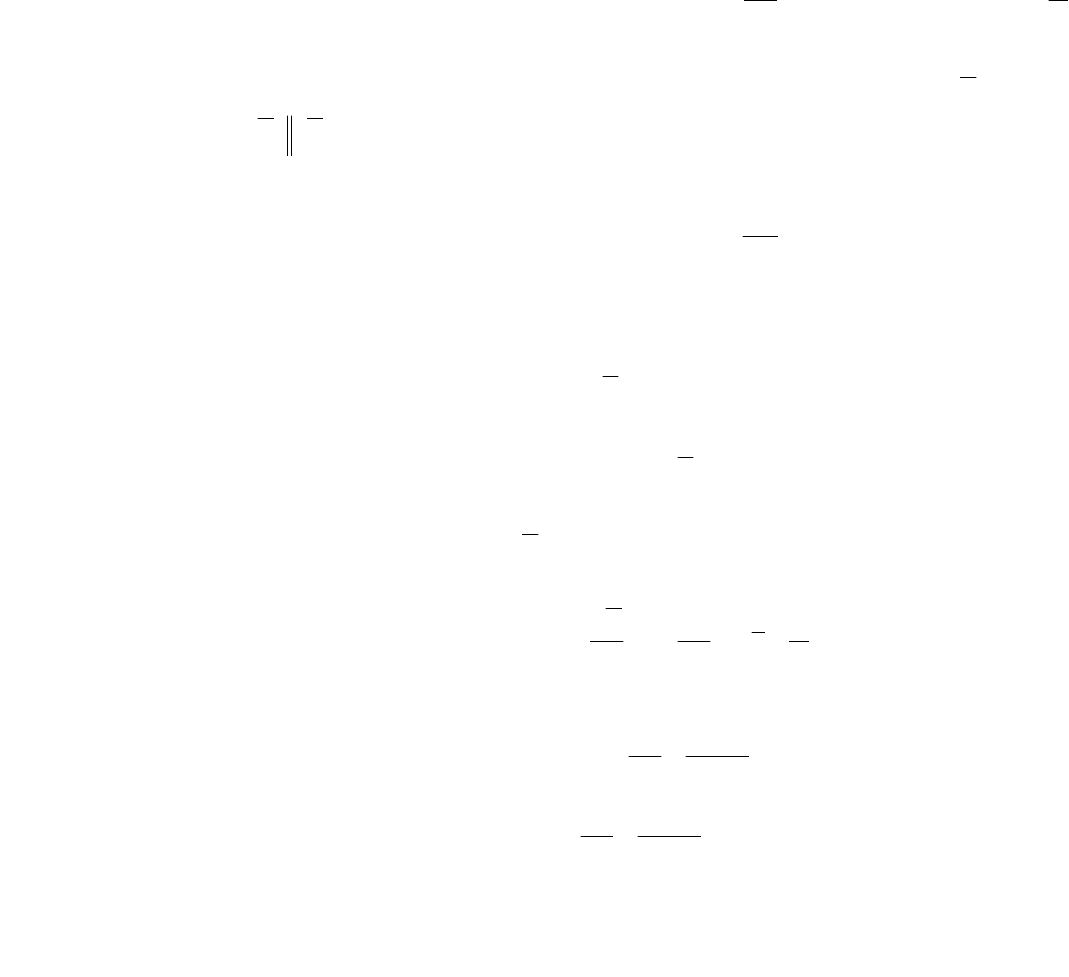
где
γ
- вес единицы объема, H –
гидравлическая высота. Тогда теорема Бернулли формулируется
следующим образом: при стационарном движении тяжелой идеальной не
сжимаемой жидкости
гидравлическая высота, равная сумме скоростной ,
2
2
g
V
пьезометрической
γ
p
и нивелирной z
высот,
сохраняет постоянное значение вдоль любой линии тока (или вихревой линии)
. Вихревой линией
называется линия, в каждой точке которой вектор вихря скорости Vrot
является касательным к данной
линии, т.е. VVrot .
Для невесомой жидкости уравнение Бернулли имеет более простой вид:
2
const.
2
V
p ρ+=
(8.8)
Первое слагаемое левой части называется пьезометрическим напором, второе –
скоростным напором
или динамическим давлением.
Потенциальные течения. Интеграл Коши – Лагранжа
Безвихревое течение, в котором ,0=Vrot
называется потенциальным. В этом случае можно ввести
скалярную функцию
ϕ
такую, что
.ϕ∇=V (8.9)
Функция
),,,( tzyx
ϕ
называется потенциалом скорости. В уравнениях Громеко–
Лэмба (8.1) исчезает
член, содержащий в явном виде
Vrot
.
Уравнения движения принимают вид
.
1
2
2
pg
V
t
V
∇−=
∇+
∂
∂
ρ
(8.10)
Для потенциального поля массовых сил П получаем
(
)
,0
2
2
=
Ρ+Π+
∇
+
∂
∂
∇
ϕϕ
t
или
(
)
).(
2
2
tf
t
=Ρ+Π+
∇
+
∂
∂ ϕϕ
(8.11)

Этот интеграл носит название
интеграла Коши – Лагранжа
. Интеграл Коши –
Лагранжа пригоден
лишь для безвихревых течений. Для несжимаемой жидкости имеем
(
)
).(
2
2
tf
p
gz
t
=++
∇
+
∂
∂
ρ
ϕϕ
(8.12)
Произвольная функция
f(t)
определяется из граничных условий.
Для стационарных течений
()const,0
ft
t
ϕ
∂
==
∂
и равенство (8.12) переходит в обычное
соотношение Бернулли.
Рассмотрим подробнее случай безвихревых течений несжимаемой невязкой жидкости:
,0.
VdivVϕ
=∇=
Для определения неизвестной функции
ϕ
получаем уравнение Лапласа
.0
=
∆
ϕ
(8.13)
Это уравнение интегрируется при заданных граничных условиях, зави
сящих от типа
поставленной задачи. Так,
в задаче об обтекании неподвижного твердого тела жидкостью, имеющей на
бесконечности заданную скорость
∞
V , следующие граничные условия:
на поверхности тела условие непроницаемости
,0=
∂
∂
n
ϕ
(8.14)
на бесконечности – невозмущенный поток
).,cos(),,cos(),,cos( zVV
z
yVV
y
xVV
x
∞∞∞∞∞∞
=
∂
∂
=
∂
∂
=
∂
∂
ϕ
ϕ
ϕ
(8.15)
Задача (8.13)-(8.15) является внешней задачей теории потенциала.
После определения потенциала скоростей
),,,( tzyx
ϕ
из интеграла Лагранжа – Ко
ши находим
давление
р
:

Задачи об истечении жидкости
Существование интегралов Бернулли, Коши –
Лагранжа ставит для величины скорости
определенный предел, превзойти который движущаяся жидкость не может без раз
рыва сплошности.
Рассмотрим установившееся безвихревое движение тяжелой несжимаемой жидкости.
Пусть в некоторой точке области на высоте
0
z
скорость и давление равны соответственно
0
V
и
0
p
;
тогда из уравнения (8.7) получаем
,
22
0
0
2
0
2
γγ
p
z
g
Vp
z
g
V
++=++
откуда
.
22
2
0
0
2
0
z
g
Vp
z
g
Vp
−−++=
γγ
Так как давление в жидкости не может быть отрицательным, то величина V не мо
жет быть
чрезмерно большой ни в одной точке. Например, для точек на той же высоте
0
zz = получ
ается
неравенство
.0
22
2
0
2
0
≥−+
g
Vp
g
V
γ
Отсюда находим предел для величины скорости V:
.
2
0
2
0
2
ρ
p
VV +≤
Если вода, находящаяся в большом сосуде, вытекает в пустоту под действием только
атмосферного давления
0
p , то на поверхности сосуда можно принять величину
0
V
близкой к нулю, и для
скорости истечения получается ограничение
ρ
0
2p
V ≤ (например, для воды при
с
м
V
м
кг
p 14,10000
2
0
≤= ).
Формула Торичелли
Интеграл Бернулли имеет фундаментальное значение в задачах гидрав
лики. Применим его для
определения скорости истечения тяжелой несжимаемой жидкости из большого открытого сосуда через
малое отверстие. Обозначим через
Σ
площадь свободной поверхности жидкости в сосуде, через
σ
-
площадь отверстия, через V и
v
- скорости на по
верхности и в отверстии, тогда из закона сохранения
массы следует
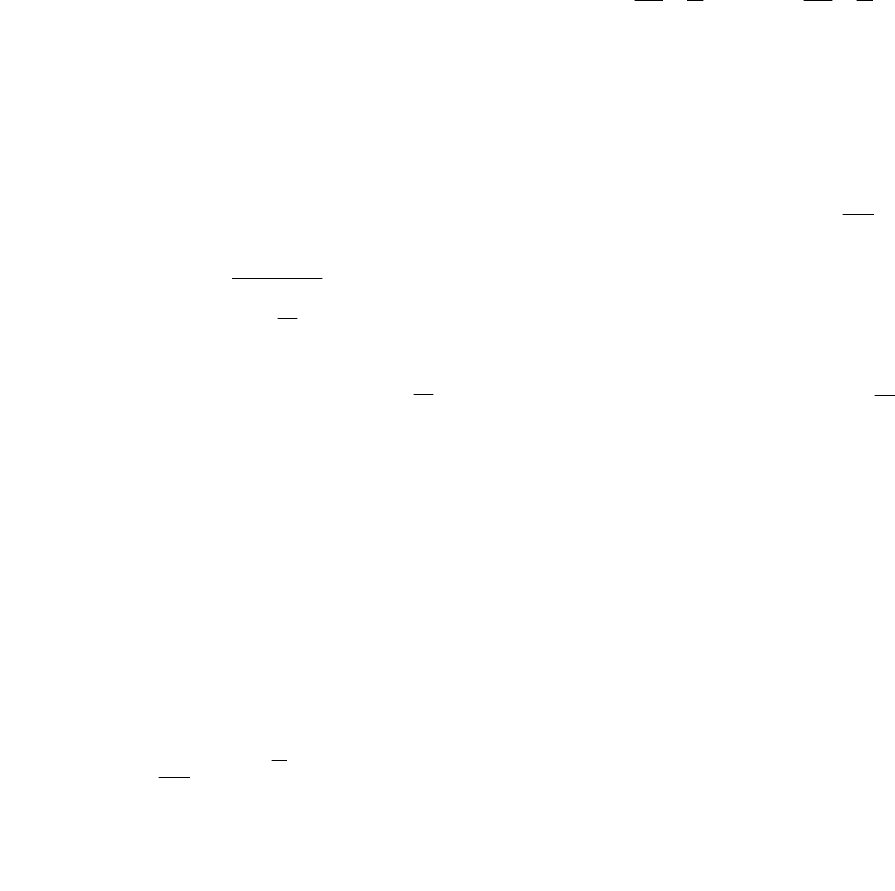
.vV
σ
=
Σ
(Поток скорости для несжимаемой жидкости через любую замкнутую поверхность равен ну
лю:
0=Σ
∫
Σ
dV
n
.)
Считая движение установившимся и безвихревым и применяя интеграл Бернулли, получим
.
2
1
2
1
2
0
2
0
V
p
gzv
p
+=−+
ρρ
Здесь начало координат взято на свободной поверхности и ось Oz
направлена вертикально вверх,
давление в отверстии на глубине (-z
), где вытекающая жидкость также образует свободную
поверхность, равно атмосферному давлению
0
p . В результате имеем
gzVv 2
22
=− или ,2
2
2
2
2
gzvv =
Σ
−
σ
откуда .
1
2
2
2
Σ
−
=
σ
gz
v
Если соотношение
Σ
σ
мало, то, пренебрегая членом ,
2
Σ
σ
получаем для скорости истече
ния
приближенную формулу Торичелли:
.2
2
gzv =
(Аналогично приближенную формулу можно получить для оценки скорости истечения газа из
большого
сосуда через малое отверстие.)
Лекция 9.
§9. Циркуляция скорости. Теоремы Томпсона, Лагранжа и Бьеркнеса
Рассмотрим циркуляционные движения идеальной жидкости и ограничимся качественными
исследованиями выведенных раньше уравнений. Уравнение неразрывности
(
)
.0=+
∂
∂
Vdiv
t
ρ
ρ
(9.1)
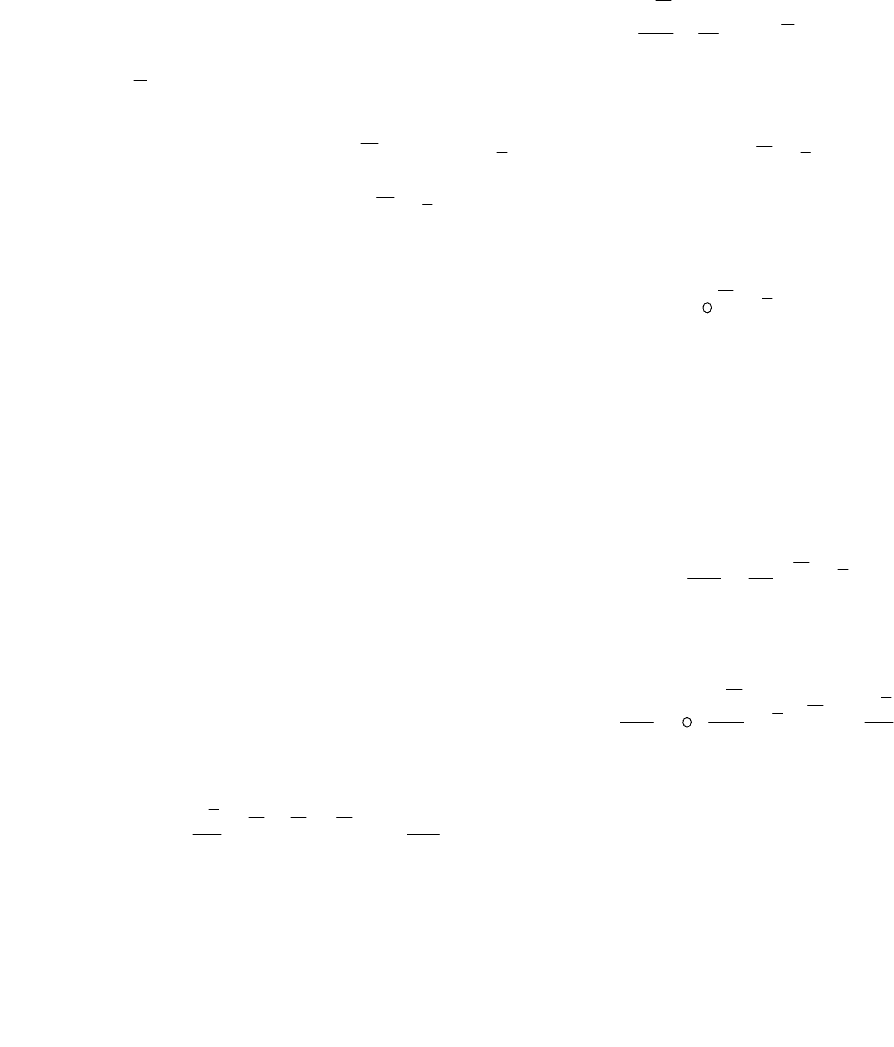
Уравнение движения
,
1
gp
dt
Vd
=∇+
ρ
(9.2)
где
g
- объемные силы.
Одной из важных характеристик гидромеханики является циркуляция скорости. Циркуляция
–
аналог работы. Пусть
F
- сила, rd - смещение, тогда rdF ⋅ - элементарная работа. Работа на какой–
либо
траектории AB равна .rdF
B
A
⋅
∫
Циркуляцией называется интеграл
,rdV
L
⋅=Γ
∫
(9.3)
взятый вдоль некоторого замкнутого контура L (т.е. аналог работы ско
рости на замкнутом контуре).
Понятие циркуляции связано с вихрем.
Рассмотрим замкнутый контур L
, состоящий из фиксированных частиц и, следовательно,
перемещающийся вместе с ними («жидкий» контур).
Найдем полную производную от интеграла (9.3) по этому контуру
.rdV
dt
d
td
d
L
⋅=
Γ
∫
Поскольку, по определению, полная производная зависит от перемещения частиц, то при
дифференцировании необходимо учесть изменение контура со временем, т.е.
.
∫
⋅+⋅=
Γ
L
dt
rd
dVrd
dt
Vd
td
d
Так как ,
2
,
2
=⋅=
V
dVdVV
dt
rd
то, используя уравнения движения (9.2), имеем

.
∫∫
−⋅=
Γ
LL
dp
rdf
td
d
ρ
(9.4)
Пусть
ω
- угловая скорость вращения (или вихрь), Vrot
2
1
=ω , для произвольного вектора
A
имеем
,Σ⋅=
∫∫
Σ
dArotnrdA
L
где
n
- нормаль к поверхности
Σ
, опирающейся на контур L.
Здесь предполагается, что контур L ограничивает односвязную область
Σ
. Для циркуляции
получаем
Σ=Σ=Γ
∫∫
ΣΣ
dndVrotn ω2
. (9.5)
Определение
. Вихревой линией называется линия, касательная к которой в каждой точке
коллинеарна вектору вихря. Уравнения этих линий:
.
zyx
dzdydx
ωωω
== (9.6)
Из вихревых линий можно образовать вихревую трубку. Для
этого возьмем замкнутый контур и
через каждую точку проведем вихревую линию.
Имеет место теорема Гельмгольца. Поток вектора вихря Vrot
2
1
=ω че
рез поперечное сечение
вихревой трубки, т.е. величина dSn
S
∫
ω , остается постоянным вдоль данной вихревой трубки.
