Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

. For low liquid water path (LWP) clouds and in the weak absorption regime, the

combination of these effects renders A approximately independent of r

. In the

strong absorption regime, these two effects combine to produce an absorption that

is a decreasing power of r

. By contrast, reﬂectance varies primarily as a function of

1=r

through the dependence of extinction on dropl et size.

Figures 13 and 14 show the reﬂectance and transmittance of a water cloud as a

function of effective radius for three different liquid water contents (LWC) and three

different wavelengths. The red lines are for wavelengths of 0:5 mm and represents the

case of no absorption. The blue and black lines are for wavelengths of 2.1 and

2:9 mm, which represent moderate and strong absorption, respectively. The previous

chapter demonstrated the inverse dependence of s

ext

on r

. Combining this with the

two-stream model, we see that cloud reﬂectance decreases as an approximate inverse

function of r

for low LWP clouds. The sensitivity between R and r

decreases with

increasing LWP and is most acute at weakly absorb ing wavelengths. The cloud

transmittance increases with increasing r

. The limit is a function of the index of

refraction.

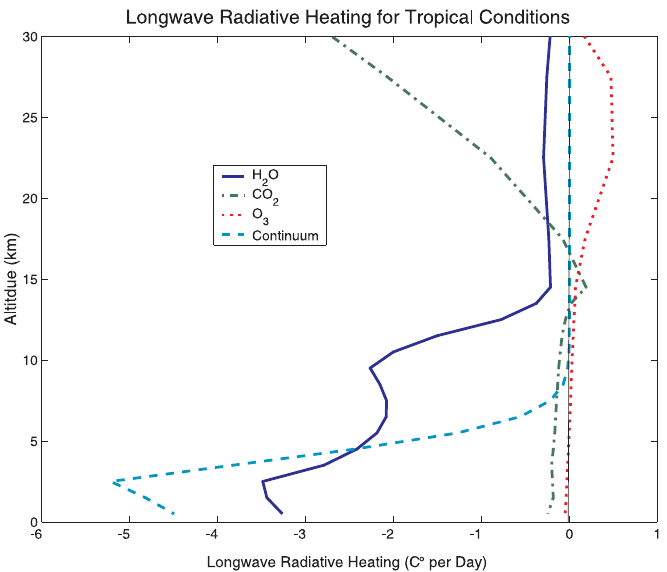
Figure 10 Longwave radiative heating for standard tropical conditions by individual gases.

See ftp site for color image.

356

RADIATION IN THE ATMOSPHERE: OBSERVATIONS AND APPLICATIONS

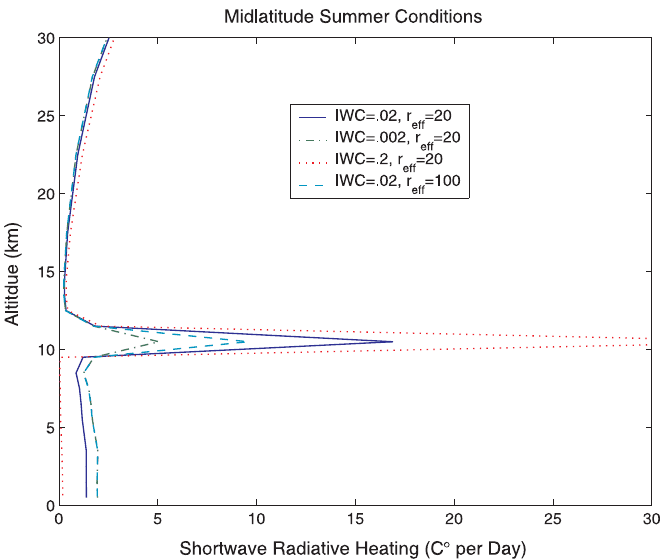
Figure 15 shows the cloud absorptance as a function of effective radius for three

different LWPs and two different wavelengths. This ﬁgure demonstrates that the

absorption of solar radiation by a cloud layer varies with size spectra in a manner

dependent on the cloud LWP. For deep clouds, with large LWPs, the absorption

increases monotonically with r

, due to the droplet radius dependence on 1  o

For thin cloud layers and low LWPs, the absorption depends on the combined effects

associated with the variation of 1  o

and s

ext

with r

. For smal l LWP, absorption

decreases with increasing r

Volcanic Aerosols

Volcanoes can inject gases and particles into the stratosphere, where the residence

times for particles are on the order of 1 year, in contrast to a residence time of 1 week

for tropospheric particles. Sulfur-bearing gases such as SO

are photochemically

converted to sulfuric acid aerosols, which quickly establish themselves as the aerosol

species. The dominant visible optical depth of the resulting particulate cloud depends

Figure 11 Impact of clouds with differing cloud microphysical properties on radiative

heating in a midlatitude summer atmosphere. Clouds are 1 km thick and the solar zenith

angle is 15



. See ftp site for color image.

3 RADIATIVE HEATING RATES 357

on the sulfur content of the volcanic efﬂuents. Thus, although Mt. St. Helens and El

Chichon injected similar quantities of ash into the stratosphere, the former caused an

optical enhancement of 10

2

at 0.55 mm over the Northern Hemis phere during the

ﬁrst year, while the latter caused an enhancement in excess of 10

1

because it was a

sulfur-rich volcano.

The single scattering albedo of the volcanic aerosols is quite close to unity

(0.995) at visible wavelengths. Thus, these aerosols can be expected to cause

Earth’s albedo to increase, temperatures in the lower stratosphere to increase, and

temperature in the troposphere to decrease. Measurements of the El Chicon cloud

imply that the thermal effects of the volcanic aerosols are important for the heat

balance of both the troposphere and stratosphere, although it dominates in the latter.

The stratospheric cloud consisted of sulfuric acid droplets with very small amounts

of volcanic ash. The particle size distribution had a mean mode radius of 0.3 mm.

Spectral measurements of optical depth show a relatively ﬂat distribution through the

visible spectrum with a peak optical depth at 0.55 mm.

The sign and magnitude of thermal infrared heating due to a stratosph eric

volcanic aerosol of a given optical depth varies signiﬁcantly with the height and

Figure 12 Impact of clouds with differing cloud microphysical properties on the longwave

radiative heating in a midlatitude summer atmosphere. Cloud is 2-km thick with a top at 10 km.

See ftp site for color image.

358

RADIATION IN THE ATMOSPHERE: OBSERVATIONS AND APPLICATIONS

latitude of the aerosols, and also with the height of the tropo spheric cloud beneath

the aerosol layer and its emissivity. The aerosol of El Chicon was mostly sulfuric

acid particles and had signiﬁcant opacity in the 760- to 1240-cm

1

window region.

Thus, the stratospheric aerosols can cause a net heating by absorption of upwelling

radiation from a warm surface; the aerosols own infrared emission is small at the

cold stratospheric temperatures.

Modeling results indicate that these volcanic particles caused a warming by the

lower stratosphere of several degrees and a cooling of the troposphere of a few tenths

by a degree over their ﬁrst year.

The largest volcanic eruption in recent history has been that of Mount Pinatubo.

Observations of the Earth Radiative Budget Experiment (ERBE) have indicating that

the aerosol is causing a net radiative cooling of Earth’s atmosphere system. The

Mount Pinatubo aerosols resulted in an enhancement of the Earth–atmosphere

albedo, with a smaller shift in the lower outgoing longwave radiation.

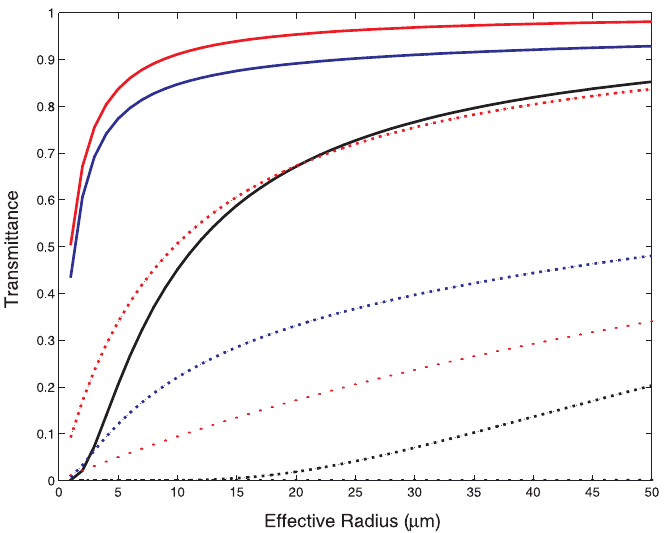
Figure 13 Impact of effective radius on transmittance as function of three wavelengths and

three ice water contents. Three wavelengths are 0.5 mm (red), 2.1 mm (blue), and 2.9 mm

(black). Liquid water content (LWC) of 0.01, 0.1, and 1 g

3

are represented by the solid,

dashed, and dotted lines, respectively. See ftp site for color image.

3 RADIATIVE HEATING RATES 359

4 TOP-OF-ATMOSPHERE RADIATION BUDGETS

If we consider the planet as a system, Ear th exchanges energy with its environment

(the solar system) via radiation exchanges at the top of the atmosphere. The balance

between radiative energy gains and radiative energy losses at the top of the atmos-

phere is referred to as the Earth radiation budget. The determination of Earth’s

radiation budget is essential to atmospheric modeling and climate studies as it

determines net energy gains and losses of the planet. Radiation budget experiments

have used satellites to measure the fundamental radiation parameters:

 Amount of solar energy received by the planet

 Planetary albedo (the portion of incoming solar radiation reﬂected back to

space)

 Emitted terrestrial radiation [also referred to as outgoing longwave radiation

(OLR)]

 Net planetary energy balance (difference between the absorbed solar energy

and the OLR)

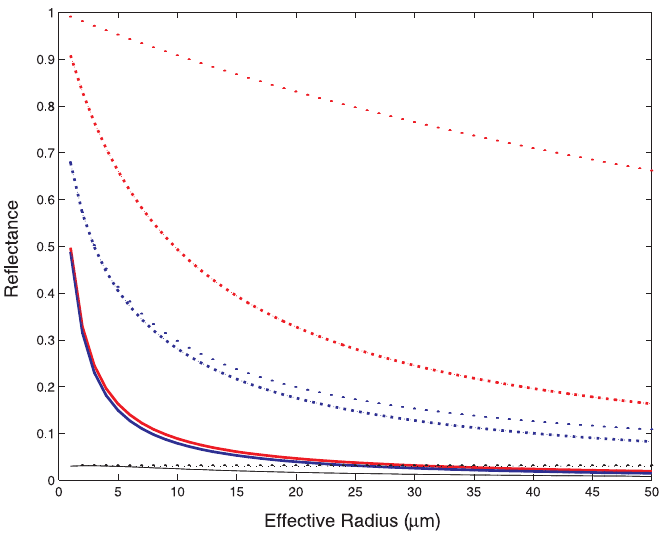
Figure 14 Impact of effective radius on reﬂectance as function of three wavelengths and

three ice water contents. Three wavelengths are 0.5 mm (red), 2.1 mm (blue), and 2.9 mm

(black). The LWC and 0.01, 0.1, and 1 g

3

are represented by the solid, dashed, and dotted

lines, respectively. See ftp site for color image.

360

RADIATION IN THE ATMOSPHERE: OBSERVATIONS AND APPLICATIONS

These elements are described in Figure 16.

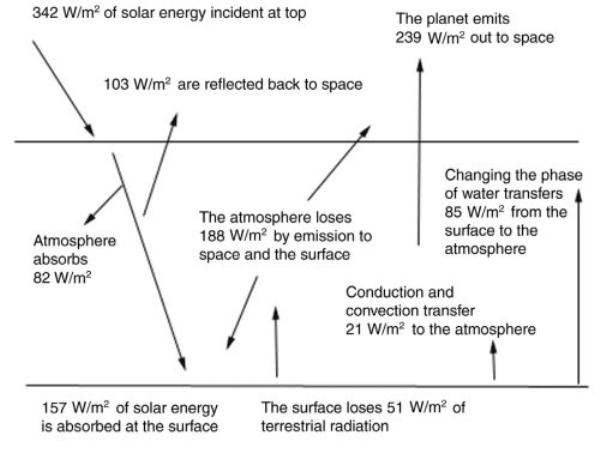
Averaged over the globe for a year, the incoming shortwave ﬂux is ðS

=4Þ where

is the solar constant, 1368 W=m

. Of this incoming energy, approximately 17%,

or 82 W=m

, is absorb ed by the atmosphere, with about 103 W=m

(30%) reﬂected

back to space (24% from the atmosphere due to clouds, aerosols, and Rayleigh

scattering and 6% from the surface). The net shortwave ﬂux at the surface is

157 W=m

, or about 53% of that incident at the top of atmosphere. In the longwave,

239 W=m

leaves Earth to balance the shortwave gain. Of this 239 W=m

, approxi-

mately 57% is due to emission by the atmosphere and 13% is due to surface

emission that is transmitted through the atmosphere. Compared to the top of the

atmosphere, the surface loses approximately 51 W=m

in the longwave, 88% of

which is absorbed by the atmosphere. The surface also gains longwave energy

emitted by the atmosphere. Thus, while the net top of atmosphere ﬂux is zero, the

surface balance is 21 W=m

. To retain energy balance the surface must lose or store

energy. Neglecting storage, the surface loses 21 W=m

, which is transferred to the

atmosphere to balance the net radiative loss. This is accomplished via latent and

sensible heat ﬂuxes. Thu s, the atmospheric radiative cooling is balanced by the latent

Figure 15 Impact of effective radius on absorption as function of three wavelengths and

three ice water contents. Three wavelengths are 0.5 mm (red), 2.1 mm (blue), and 2.9 mm

(black). The LWP of 10, 100, and 1000 g

2

are represented by the solid, dashed, and dotted

lines, respectively. See ftp site for color image.

4 TOP-OF-ATMOSPHERE RADIATION BUDGETS 361

heat of condensation, which is released in regions of precipitation, and by conduc-

tion of sensible heat from the surface.

Earth’s Top of the Atmosphere Radiation Budget

Independent satellite observations of the longwave emitted energy to space have

indicated that on a global annual mean basis, the absorbed solar radiation is in

balance with the outgoing longwave radiation (to within instrument noise). This

balance exists on a hemispherical scale, indicating that there is little net cross-

equatorial energy transport.

Seasonal and latitudinal variations in temperature are driven by the variations in

the incoming solar radiation. Measurements of the solar insolation at the top of the

atmosphere are important, since it is the primary climate external forcing mechan-

ism. Meth ods of calculating these variations have already been discussed. Measure-

ments from satellites indi cate that there are small variations in the solar insolation,

on the order of 0.1 to 0.3%.

The global annual averaged albedo is approximately 0.30. The globally and

annually averaged planetary albedo is a key climate variable since it, combined

with the solar insolation, determines the radiative energy input to the planet. Varia-

tions in the global mean albedo result from the eccentricity of Ear th’s orbit and

geographical differences between the Northern and Southern Hemispheres. The

annual average albedo of the Northern and Southern Hemispheres is nearly the

same, demonstrating the important inﬂuence of clouds.

Figure 16 Average annual global energy budget in W=m

362

RADIATION IN THE ATMOSPHERE: OBSERVATIONS AND APPLICATIONS

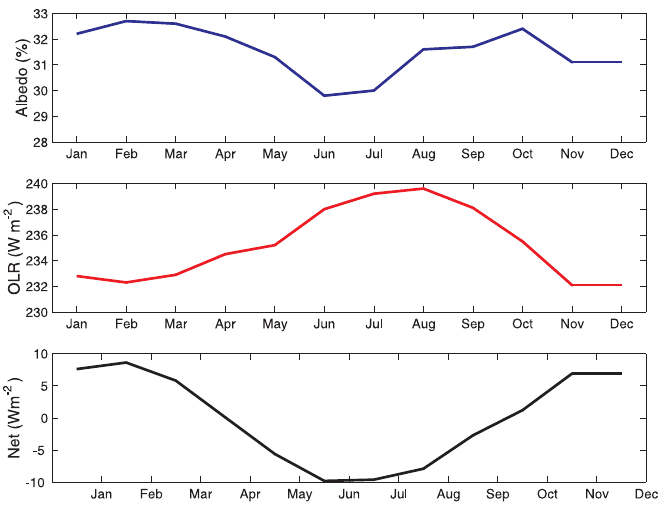
There are signiﬁcant variations in the month-t o-month global mean albedo, long-

wave, and net ﬂux (Fig. 17). The annual cycle in the global monthly means are due

to Earth’s orbit about the sun and the geographical differences between the Northern

and Southern Hemispheres. The range in the OLR throughout the year is approxi-

mately 10 W=m

, with a maximum in July and August. This maximum results from

there being more land in the Northern Hemisphere than the Southern. The annual

average global albedo is approximately 30%, with an amplitude of approximately

2%. The planetary albedo reaches a maximum around October and November. This

albedo variation reduces the impact of the annual variation in incoming solar radia-

tion on the net radiation budget .

The amplitude of the annual cycle of globally averaged net ﬂux is approximately

26 W=m

. This is similar to the peak-to-peak amplitude in the external forcing

associated with variations in the solar insolati on due to Earth–sun geometry. The

interannual variation of the hemispherical averaged net ﬂux shows maximum heating

during the summer with the largest changes occurring for the transition from solstice

to equinox.

The zonal annual average absorbed solar radiation exceeds the outgoing long-

wave radiation in the tropical and subtropical regions, resulting in a net radiative

heating of the surface–atmospheric column; while in the mid to polar latitudes there

Figure 17 Annual variation in planet’s energy budget components: albedo (top), OLR

(middle), and net radiation (bottom). See ftp site for color image.

4 TOP-OF-ATMOSPHERE RADIATION BUDGETS 363

is a net divergence (Fig. 17). This equator-to-pole gradient in radiative energy is the

primary mechanism that drives the atmospheric and oceanic circulations. On an

annual and long-term basis no energy storage and no change in the global mean

temperature occurs, so the zonal mean radiative budget must be balanced by

meridional heat transport by the atmosphere and oceans.

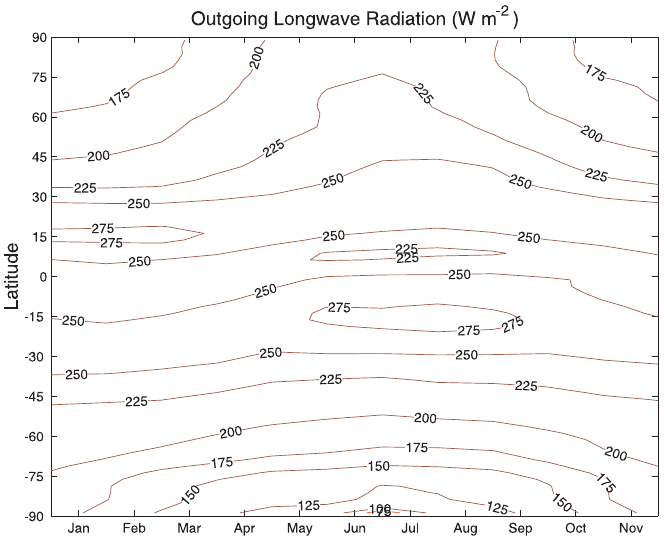
The minimum in emitted ﬂux by the planet located near the equator is due to the

high cloud tops associated with the Inter-Tropical Convergence Zone (ITCZ)

(Fig. 18). This minimum migrates about the equator as seen in the seasonal proﬁles

and is seen as a maximum in albedo. Note also the large emission in the vicinity of

the subtropical highs and the corresponding lower albedos. The lowest values of

OLR are associated with the Antarctic plateau in wi nter. This region is very cold and

the high altitude means that most of the surface-emitted radiation escapes to space.

Maximum OLR occurs in the tropics. Throughout the year the OLR slowly increases

toward the summer hemisphere.

The largest albedos are associated with the polar regions, which are snow covered

and have high solar zenith angles. The increasing albdeo with latitude is, in general,

due to the increasing solar zenith angle (Fig. 19). In the Northern Hemisphere the

albedo is larger in summer than winter, due to the increase in cloud cover and optical

Figure 18 Annual cycle of monthly mean OLR in W=m

2

determined from ERBE

observations. See ftp site for color image.

364

RADIATION IN THE ATMOSPHERE: OBSERVATIONS AND APPLICATIONS

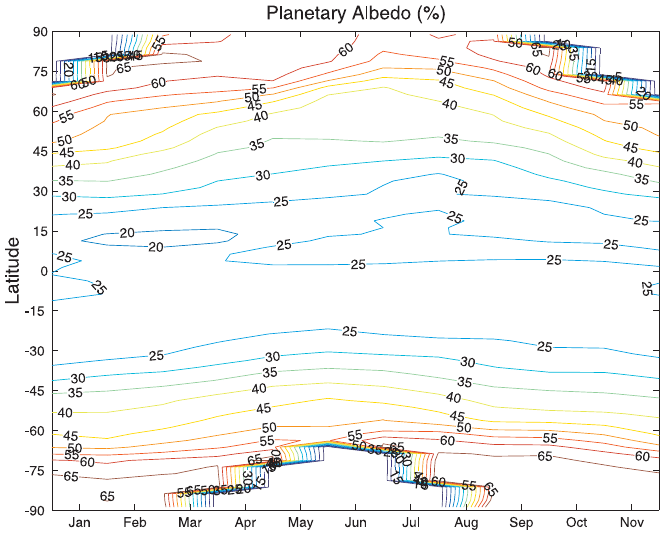
thickness. In the tropical regions the albedo variation is inﬂuenced primarily by

weather disturbances and their associated cloud distributions. In the polar region,

variations are due to the distribution of major ice sheets and the decreasing mean

solar elevation angle with latitude. The annual variation in the zonal mean absorbed

solar radiation follows the variation of the solar declination due to the annual

variation of the incoming solar energy being greater than the annual variation of

the albedo. The net energy also exhibits this same dependency.

There are net radiation energy gains in the tropics and subtropics with energy

losses over the polar regions (Fig. 20). The region of net energy gains tracks the

solar declination. Differences between the Northern and Southern Hemispheres

result from differences in land distributions. While the minimum OLR occurs

over Antarctica, the minimum net losses occur between approximate 60 S and

70 S. Maximum energy gains occur in the Souther n Hemisphere subtropica l regions

during December and Januar y. Differences between land and water are more evident

in a regional analysis of Earth’s radiation budget.

Figures 21 and 22 are the ERBE measured January and July OLR. Maximum

OLR occurs over the deserts and cloud free ocean regions of the subtropica l highs.

Relative minimums in tropical regions result from high, thick cir rus associated with

Figure 19 Annual cycle of monthly mean albedo in percent determined from ERBE

observations. See ftp site for color image.

4 TOP-OF-ATMOSPHERE RADIATION BUDGETS 365