Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

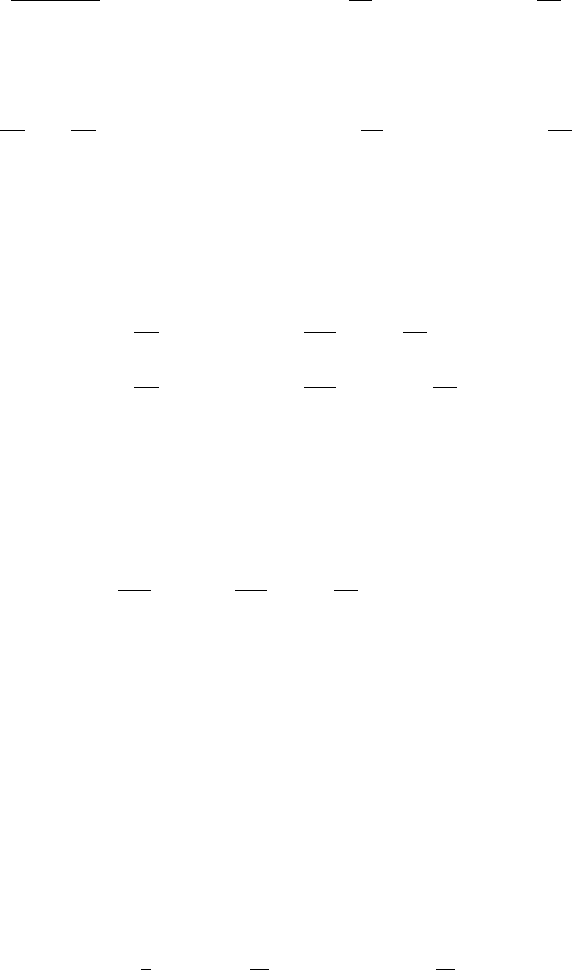
Now we can evaluate the scattering integral

dðI

þ I

mÞ

¼ I

þ I

m  o

ðI

þ I

gmÞ

ð1  3gmm

ÞF

exp

t



ð80Þ

and rearrange terms

þ m

¼ I

ð1  o

ÞþI

mð1  o

gÞ

ð1  3gmm

ÞF

exp

t



ð81Þ

We can break (81) into two pieces by observing that it contains both odd and even

powers of m. What we will do, then, is integrate the equation over m from 1to1,

which will leave only terms in even powers of m. We then multiply (81) by m and

repeat the integration. The two resulting equations are

¼ 3ð1  o

ÞI



exp

t



ð82Þ

¼ð1  o

gÞI

exp

t



ð83Þ

Equations (82) and (83) are a set of two ﬁrst-order coupled linear differential equa-

tions. We can uncouple the equations and ﬁnd a solution by differentiating one

equation with respect to optical depth and substituting the other. This yields, for

example

¼ k



exp

t



ð1 þ g  o

gÞð84Þ

where we have deﬁned the eigenvalue k

¼3(1o

)(1o

g). The solutions to (84)

and the analogous equation for I

are a sum of exponentials in kt, i.e.,

¼ Ae

þ Be

kt

þ ce

t=m

ð85Þ

where A, B, and c are determined from the boundary conditions at the top and

bottom of the medium and from the particular solution.

The general solution is very complicated but is tractable in some limits. The

simplest case is a single homogeneous layer of total optical depth t* over a non-

reﬂective surface. If the layer is optically thin (t* 1), the reﬂected and transmitted

ﬂuxes are

R ¼ o

 3gm





T ¼ 1  R 





ð1  o

Þð86Þ

336 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

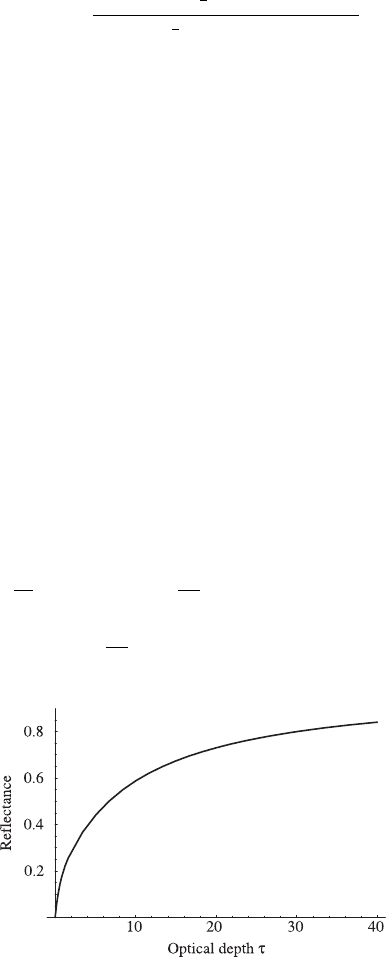
If the layer doe s not absorb (i.e., if o

¼0), the reﬂected ﬂux is

R ¼

ð1  gÞt



 m



ð1  e

t



þð1  gÞt



ð87Þ

Reﬂectance increases with optical thickness, rapidly at ﬁrst and then more slowly

as shown in Figure 11. Reﬂectance at a given optical depth also increases as m

decreases (this is not shown), since the radiation must change direction less drasti-

cally to be reﬂected into the upward hemisphere. Decreases in the asymmetry para-

meter increase the amount of reﬂection, since photons are more likely to be scattered

backwards, and since most photons, especially near cloud top, are headed down-

ward. Even relatively optically thick clouds transmit at least 20% of the ﬂux incident

on them, which is why it is not pitch dark at the surface even on very cloudy days.

Computing Flux: Two-Stream Model

Eddington’s approach to the radiative transfer equation is to expand both the inten-

sity and the phase function to ﬁrst order in angle; the ﬂux can be computed once the

approximate intensity ﬁeld is known. In the two-stream model we ﬁrst average the

radiative transfer equation and the phase function to get a differential equation for

ﬂuxes; then we compute the solution . The solutions are quite similar, as we expect

them to be, and the choice of exactly which method to use is a little arbitrary.

Let us begin with the azimuthally averaged radiative transfer equation (71) and

integrate it over each hemisphere to ﬁnd the ﬂux. Ignori ng emission, we have for the

downward ﬂux

1

dm ¼

1

Idm 

1

Pðm

! mÞIðm

Þdm



Pðm

! mÞF

expðt=m

Þdm

ð88Þ

Figure 11 Reﬂectance of a nonabsorbing layer as computed from the Eddington approx-

imation. The solar zenith angle is 60



8 SOLVING THE RADIATIVE TRANSFER EQUATION SIMPLY 337



¼ F



1

Pðm

! mÞI

ðm

Þdm



1

Pðm

! mÞI

ðm

Þdm



Pðm

! mÞF

exp

t



ð89Þ

Implicit in going from (88) to (89) is a choice about the ratio:



mm ¼

1

ð90Þ

Different two-stream approximations differ in this choice. We then make use of the

reciprocity of the phase function and deﬁne the backscattering coefﬁcients:

bðmÞ¼

1

Pðm

! mÞdm

b ¼

bðmÞdm ð91Þ

which deﬁne the fraction of ﬂux scattered into the opposite hemisphere. Applying

these deﬁnitions, and doing the analogous calculation for the upward ﬂux, we arrive

at the two-stream equations:



¼ F

 o

ð1  bÞF

þ o



½1  bðm

ÞF

exp

t



ð92Þ



¼ F

 o

ð1  bÞF

þ o



bðm

ÞF

exp

t



ð93Þ

These are two ﬁrst-order, linear, coupled differential equations with constant

coefﬁcients. They can be uncoupled by differentiating one with respect to optical

thickness, then substituting the other. As with the Eddington approximation, the

complete solution for reﬂected or transmitted ﬂux is the sum of exponentials in

optical thickness, with coefﬁcients determined by the boundary conditions.

9 SOLVING RADIATIVE TRANSFER EQUATION COMPLETELY

Analytic approximations like the Eddington and two-stream methods are useful and

often accurate enough for ﬂux calculations. If intensity is required, though, we must

ﬁnd numerical ways to solve the radiative transfer equation. In numerical weather

338 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

prediction, the continuous Navier–Stokes equations of motion are approximated by

ﬁnite differences between points on a spatial grid. The integrals in the radiative

transfer equation are over direction, so the discretization is over angle, turning the

continuous equation into one at discrete ordinates or directions. There are two

popular approaches to solving this equation, which of course give the same num-

erical results.

Adding–Doubling Method

Imagine two layers, one of which overlies the other. The upper layer has ﬂux

transmittance and reﬂectance T

and R

, and the lower layer T

and R

.How

much total ﬂux R

is reﬂected from the combination of layers? Some ﬂux is reﬂected

from the ﬁrst layer (R

); some of the ﬂux transmitted through the ﬁrst layer is

reﬂected from the second layer and transmitted through the ﬁrst layer (T

);

some of this ﬂux reﬂected from the second layer is reﬂected back downwards,

where some portion is reﬂected back up (T

), and so on. Because reﬂection

and transmission are both less than one, we can use the summation formul a for

geometric series to compute the total reﬂection:

¼ R

þ T

þ

¼ R

þ T

½1 þ R

þ R

þT

¼ R

þ T

½1 þ R



1

ð94Þ

where the term in square brackets accounts for the multiple reﬂections between the

layers. There is a similar relation for transmission.

Equation (94) and its analog for transmission may be combined with the trans-

mission and reﬂection results from the Edd ington or two-stream solutions to

compute the transmittance and reﬂectance of layered atmospheres, in which the

single scattering albedo or asymmetry parameter changes with optical thickness,

or to account for a reﬂecting surface beneath the atm osphere.

The adding–doubling method extends this idea to intensity by replacing the

reﬂection and transmission terms in (94) with matrices that account for the forward

and backward scattering from one polar angle into another. Rather than beginning

with analytical results for arbitrary layers, we ﬁnd R and T for a layer of optical depth

dt 1, assuming that photons are scattered no more than once. The reﬂection and

transmission of a layer of 2dt can be computed using (94) and the reﬂection and

transmission matrices for the original layer. Repeating this process we can ﬁnd the

reﬂection and transmission of arbitrari ly thick layers. Arbitrarily complicated atmos-

pheres can be built up by superimposing layers with different properties and comput-

ing the reﬂection and transmission matrices for the combination. Reﬂection from

surfaces ﬁts naturally into the adding framework.

9 SOLVING RADIATIVE TRANSFER EQUATION COMPLETELY 339

Eigenvector Solutions

As an alternative to the adding–doubling method we can approximate the continuous

radiative transfer equation with a version that is discrete in polar angle





t r











ð95Þ

where I



are vectors containing the intensity I(m

) at each of N angles (each discrete

ordinate). The t and r matrices contain the phase function information:

j;j

Pðm

! m

Þ1

j;j

Pðm

!m

Þð96Þ

and the source vector is



1

Pðm

!m

ÞF

t=m

ð97Þ

To solve the matrix version (95) of the radiative transfer equation, we treat the

homogeneous equation as an eigenvector problem. That is, we set the source term

to zero and substitute solutions of the form I



¼G



kt

. This results in

t r







¼ k





ð98Þ

The solution for intensity is then a sum of the eigenvectors and the particular

solution for the source term, with weights determined from the boundary conditions.

The solution can be extended to more than one layer by ensuring that intensities

match at the layer boundaries. This technique is usually called ‘‘discrete ordinates’’

in the scientiﬁc literature, though many solutions use discrete forms of the radiative

transfer equation.

Radiative Transfer in Two and Three Dimensions

In our development of the radiative transfer equation we assumed that the atmos-

phere varies only in the vertical, which leads to a radiation ﬁeld that depends only on

direction and vertical position. But the real atmosphere varies in the horizontal as

well as the vertical. In particular, cloud optical properties can change dramatic ally

over relatively short distances. A full description of a radiation ﬁeld depends on

horizontal position as well as vertical position and direction, and in the three-

dimensional radiative transfer equation the derivative becomes a gradient operator

to account for transfers in the horizontal as well as the vertical.

Traditionally, radia tive transfer in two and three dimensions has been computed

using Monte Carlo integration techniques. The domain is divided into discrete

340 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

volumes, within which the optical properties (extinction coefﬁcient, single scattering

albedo, and phase function) are consi dered constant. The paths of many, many

photons are then traced from their source until they leave the domain. In solar

radiation calculations, for example, the photons are typically introduced at the top

of the domain, then travel a random distance depending on the amount of extinction

they encounter along the trajectory. They then undergo a scattering and=or absorp-

tion event, and continue in a new direction related to the scattering phase function;

this process continues until they exit the domain. Monte Carlo methods are best

suited to the computation of domain-averaged quantities, but are very ﬂexible. An

alternative is to estimate the radiation ﬁeld at each grid point, then iterate until the

ﬁeld is self-consistent.

Three-dimensional radiative transfer is much more computationally expensive

than one-dimensional calculations, and it is difﬁcult to measure atmospheric proper-

ties well enough to provide useful input ﬁelds. Three-dimensional effects can be

signiﬁcant, however, especially in remote-sensing applications.

10 FROM THEORY TO APPLICATIONS

In this chapter we have laid out the foundations of radiative transfer. We have

discussed the physical mechanisms that underlie absorption and scattering and

talked about ways to compute the quantities needed for remote-sensing and

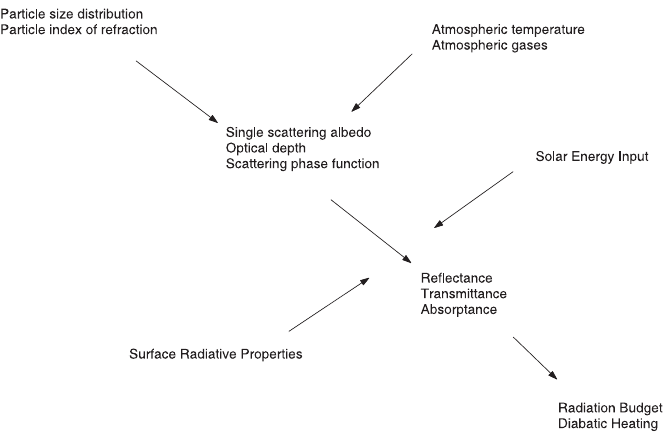
Figure 12 Topics in radiative transfer and remote sensing. This chapter has covered the

upper half of the diagram, as well as the computation of reﬂectance, transmittance, and

absorptance; the other topics are discussed in the next chapter.

10 FROM THEORY TO APPLICATIONS 341

energy budget applications. The relationship between the various topics, and those to

be covered in the following chapter, is shown in Figure 12.

In day-to-day practice much of this work is routine. There are codes available to

compute the absorption spectrum of an arbitrary atmosphere, to compute the single

scattering parameters of individual particles, and any number of models available for

solving the radiative transfer equati on, each of which is tailored to a speciﬁc appli-

cation. An understanding of the underlying theory is essential for a critical assess-

ment, but most current research in radiative transfer is in the applications, that we

discuss in the next chapter.

342 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

CHAPTER 20

RADIATION IN THE ATMOSPHERE:

OBSERVATIONS AND APPLICATIONS

STEVEN A. ACKERMANN AND ROBERT PINCUS

1 OVERVIEW

The previous chapter discussed the physical mechanisms that underlie absorption

and scattering and presented approaches to compute the quantities needed for remote

sensing and energy budget applications. In this chapter we discuss observations of

radiative ﬂuxes and apply the equations to remote sensing the atmosphere. The

boundary conditions at the top and bottom of the atmosphere are required to

compute the transfer of radiation through the atmosphere. Thus, the chapter

begins by describing the boundary conditions at the top of atmosphere and at the

surface. These conditions are then used to calculate the radiative heating of the

atmosphere in the next section. After discussing radiative heating proﬁles, observa-

tions of the energy budget at the top of atmosphere are presented, followed by a

discussion of the greenhouse effect.

Satellite observations are routinely used to help answer the question ‘‘What is the

weather like?’’ In addition, satellite observations are routinely used to determine the

state of Earth’s surface as well as cloud properties. Section 6 provides examples of

satellite remote sensing the surface and atmospheric conditions.

2 BOUNDARY CONDITIONS

The boundary conditions at the top and bottom of the atmosphere include the

properties of the surface and the incoming solar radiation at the top of the

Handbook of Weather, Climate, and Water: Dynamics, Climate, Physical Meteorology, Weather Systems,

and Measurements, Edited by Thomas D. Potter and Bradley R. Colman.

ISBN 0-471-21490-6 # 2003 John Wiley & Sons, Inc.

343

atmosphere. To determine the amount of incoming solar radiation, we must consider

the sun–Earth geometric relationships.

The Sun and Its Relationship to Earth

Earth receives energy from the sun. This energy drives atmospheric and oceanic

circulations. In this section we brieﬂy discuss some of the properties of the sun

before presenting methods of computing sun–Earth astronomical relationships.

The sun, which primarily consists of hydrogen and helium, is 4.6 billion years old

and is approximately 1:5  10

km from Earth. The radius of the sun is approxi-

mately 700;000 km with a mass of 2  10

g. The temperature of the sun is about

5  10

K at center decreasing to about 5800 K at the surface.

As with the Earth’s atmosphere, the sun can be categorized into different layers,

including the photosphere, corona, and the chromosphere. The photosphere is the

visible region, or the surface of the sun with a thickness of approximately 500 km

within which the temperature decreases from 8000 to 4000 K. The photosphere is

often marked by features called sunspots, which are associated with convection of

the sun’s hot gases. Sunspots do not occur in the polar regions of the sun. The

sunspot minima and maxima occur in a cycle that has a period of approximately

11 years. During sunspot maxima the sun is disturbed with particle outbursts and

solar ﬂares. During sunspot minima the sun is quiet or less active. Pairs of sunspots

often have opposite magnetic polarities. For a given sunspot cycle, the polar ity of the

leading spot is always the same for a given hemisphere. With each new sunspot cycle

the polarities reverse; thus, the sunspot cycle is often thought of as a 22-year period.

Sunspots appear as dark spots on the surface because these areas are at lower

temperatures than the surrounding surface; however, satellite measurements show

that more radiation is emitted during a sunspot maximum than a sunspot minimum.

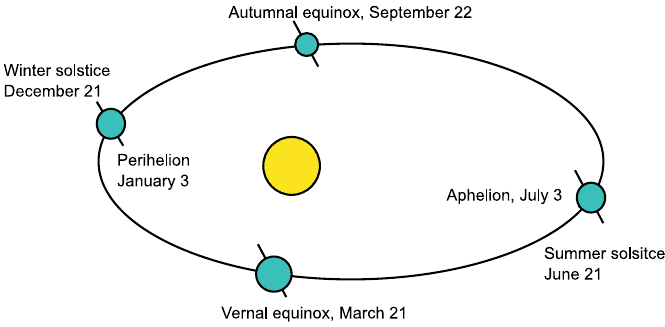
Figure 1 Earth’s orbit around the sun. See ftp site for color image.

344

RADIATION IN THE ATMOSPHERE: OBSERVATIONS AND APPLICATIONS

This may result from increased emission by the faculae, which are bright areas

around the sunspots.

The chromosphere extends up to 5000 km above the photosphere. The tempera-

ture ranges from 4000 to 6000 K near the photosphere and increases to 10

Kat

5000 km. The corona, which can be thought of as the sun’s atmosphere, extends

from the solar disk outward many millions of kilometers. The corona is visible

during total solar eclipses. The stream of gas that ﬂows out of the corona and into

the solar system is called the solar wind, which provides the energy to produce

Earth’s aurora borealis and aurora australis.

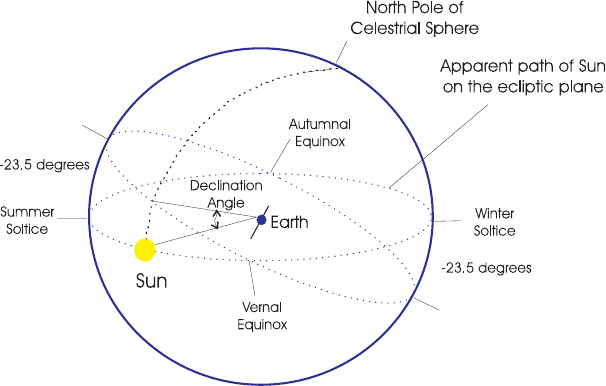
Sun–Earth Astronomical Relationships

To calculate the solar ﬂux distribution within the atmosphere and ocean, we need to

know where the sun is with respect to the geographical region of interest. Such

relationships are depicted in Figures 1 through 3 and formulated below.

The mean sun–Earth distance, r

, is deﬁned to be one astronomical unit (1 AU).

The minimum sun–Earth distance (perihelion) is about 0.983 AU and occurs on

approximately Januar y 3. The maximum distance (aphelion) is 1.1017 AU and

occurs on approximately July 3. The sun–Earth distance, r, is known accurately

for every day of the year and is published in the American Ephemeris and Nautical

Almanac; however, for applications in atmospheric radiative transfer, mathematical

approximations are simpler to use. What is required is the reciprocal of the square of

Figure 2 Deﬁnition of Sun-Earth astronomical relations. See ftp site for color image.

2 BOUNDARY CONDITIONS 345