Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

ments, for example, usually have a ﬁnite ﬁeld of view and a ﬁnite spectral sensitivity;

interpreting measurements from these sensors therefore requires calculations of

intensity, which may be broadband, narrowband, or essentially monochromatic,

depending on the detector.

Imagine, though, wanting to compute the rate at which radiation heats or cools a

layer of air in the atmosphere. Here we need to know the net amount of energy

remaining in the layer, which we can calculate by considering the decrease in both

upwelling and downwelling ﬂu xes as they cross a layer between z

and z

¼ F

ðz

ÞF

ðz

ÞþF

ðz

ÞF

ðz

¼ F

ðz

ÞF

ðz

Þ½F

ðz

ÞF

ðz

Þ

¼ F

net

ðz

ÞF

net

ðz

ð7Þ

where we have deﬁned the net ﬂux as F

net

(z) ¼F

(z)F

;

(z). As z

and z

get very

close together, the difference in (7) becomes a differential, and the rate of heating

can be related to the divergence of the radiative ﬂux though the air density r and heat

capacity c

dTðzÞ

¼

net

ðzÞ

ð8Þ

3 SOURCES OF RADIATION

Imagine setting a cast-iron skillet over a really powerful burner and turning on the

gas. At ﬁrst the pan appears unchanged, but as it heats it begins to glow a dull red.

As the pan becomes hotter it glows more brightly, and the color of the light changes

too, becoming less red and more white.

In the idealized world inhabited by theoretical physicists, the cast-iron skillet is

replaced by a block. The block has a cavity inside it and a small hole opening into

the cavity. The block can be heated to any temperat ure. Measurements of the radia-

tion emerging from this cavity show that:

1. The spectral intensity B

emerging from the cavity at each wavelength depends

only on the temperature T of the block, and not on the material or the shape of

the cavity.

2. The total amount of energy emitted by the cavity increases as the temperature

increases.

3. The wavelength at which B

reaches its maximum value decreases with

temperature.

306 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

The Planck Function

A theoretical explanation for cavity radiation was the single most compelling

unsolved problem in physics at the beginning of the twentieth century. The best

ﬁt to observations had been suggested by Wien:

ðTÞ¼

=lT

ð9Þ

where c

and c

were determined experimentally. In October 1900 Max Planck

proposed a small modiﬁcation to this relationship, namely

ðTÞ¼

=lT

 1

ð10Þ

Planck’s relationship, now called the Planck function, was a better ﬁt to the data

but was not an explanation for why radiation behaves this way. To develop a theo-

retical model, Planck imagined that the atoms in the cavity walls behave like tiny

oscillators, each with its own characteristic frequency, each emitting radiation into

the cavity and absorbing energy from it. But it proved impossible to derive the

properties of cavity radiation until he made two radical assumptions:

1. The atomic oscillators cannot take on arbitrary values of energy E. Instead, the

oscillators have only values of E that satisfy E ¼nhn where n is an integer

called the quantum number, n the oscillator frequency, and h a constant.

2. Radiation occurs only when an oscillator changes from one of its possible

energy levels to anothe r; that is, when n changes value. This implies that the

oscillators cannot radiate energy continuously but only in discrete packets, or

quanta.

By Dece mber of 1900 Planck had worked out a complete theory for cavity

radiation, including the values of c

and c

¼ 2hc

ð11Þ

In these equations k is Boltzmann’s constant, which appears in statistical mechanics

and thermodynamics, and h is Planck’s constant. Planck used observations of B

(T )

to determine the values h ¼6.63 10

34

J=s and k ¼1.38 10

23

J=K. Equations

(10) and (11) were the basis for the development of quantum mechanics, which

fundamentally changed the way physicists looked at the world.

3 SOURCES OF RADIATION 307

Blackbody Radiation and Its Implications

In the atmospheric sciences we refer not to cavity radiation but to blackbody radia-

tion, a blackbody being anything that radiates according to (10). Blackbody radiation

is isotropic, meaning that it is emitted in equal amounts in all direc tions.

Wavelength of Maximum Emission

The wavelength at which blackbody radiation reaches its maximum intensity can be

found by taking the derivative of B

(T ) with respect to wavelength, setting the result

to 0, and solving for l. That is, we solve

ðTÞ

¼ 0 ð12Þ

for the wavelength l

max

, which yields Wien’s displacement law

max

¼ 2898 mm K=T ð13Þ

At temperatures typical of Earth’s atmosphere (say, T ¼288 K), the maximum wave-

length is about 10 mm in the infrared portion of the spectrum, while the sun (at a

temperature about 5777 K) is brightest at about 0.5 mm, where visible light is green.

Total Amount of Energy Emitted

How much energy does a blackbody radiate at a given temperature? This quantity

is the blackbody broadband intensity and is computed by integrating over all

wavelengths:

BðTÞ¼

ðTÞdl ¼

ð14Þ

Equation (14) is the Stefan–Boltzmann relation and makes use of the Stefan–

Boltzmann constant s ¼5.67 10

8

W=m

4

. Because blackbody radiation is

isotropic, the total amount of radiation lost by an object into each hemisphere is

FðT Þ¼

BðTÞm dm dj ¼ sT

ð15Þ

Figure 2 shows B

(l, T ) plotted for two values of T, roughly corresponding to the

average surface temperatures of Earth and sun. The curves are each normalized,

since otherwise the much greater intensity produced at solar temperatures would

swamp the intensity produced by terrestrial objects. Almost all the sun’s energy is

produced at wavelengths less than about 4 mm, while almost all the energy emitted

308 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

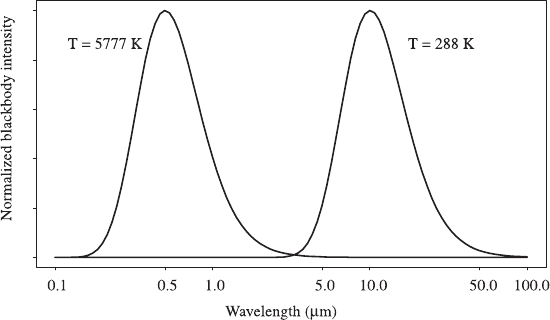
by Earth is produced at wavelengths longer than 4 mm; this convenient break lets us

treat solar radiation and terrestrial radiation as independent.

Blackbody radiation helps us understand the light produced by our cast-iron

skillet. The pan emits radiation even at room temperature, although the emission

is mostly in the infrared por tion of the spectrum. As the skillet is heated, the total

amount of radiation emitted increases (as per the Stefan–Boltzmann relation) and the

wavelength of maximum emission gets shorter (as per Wien’s displacement law)

until some of the emission is in the longer (red) part of the visible spectrum. If the

pan were made even hotter, it would glow white, like the ﬁlament in an incandescent

light bulb.

Emissivity, Energy Conservation, Brightness Temperature

The radiation emitted by any object can be related to the blackbody radiation

ðTÞ¼e

ðTÞð16Þ

where e

is the emissivity of the object, which varies between 0 and 1. If e

does not

depend on wavelength, we say that the object is a gray body; a blackbody has a value

of e

¼1.

How are emission and absorption related? Imagine an object that absorbs

perfectly at one wavelength but not at all at any other wavelength (i.e., an object

with e

¼1 at one value of l ¼l* and e

¼0 everywhere else), illuminated by

broadband blackbody radiation from a second body. The object absorbs the incident

radiation and warms; as it warms the emission (which occurs only at l *, remember)

increases. Equilibrium is reached when the amount of energy emitted by the particle

out

is equal to the amount absorbed E

. At wavelength l the body acts as a

Figure 2 Blackbody intensity B

as a function of wavelength for temperatures correspond-

ing to the surfaces of Earth and sun. The curves are arbitrarily normalized.

3 SOURCES OF RADIATION 309

blackbody, so emission depends only on the equilibrium temperature and

out

¼I

(T ) ¼B

(T ). The body is exposed to broadband blackbody radiation, so

¼B

(T ). But since equilibrium implies that E

¼E

out

, the absorption at every

wavelength other than l* must be zero. This chain of reasoning, known as Kirchoff’s

law, tells us that the absorptivity and emissivity of objects is the same at every

wavelength.

The Planck function ﬁnds another application in the computation of brightness

temperature. If we make measurements of monochromatic intensity I

at some

wavelength l, and assume that e

¼1, we can invert the Plank function to ﬁnd

the temperature T

at which a blackbody would have to be in order to produce

the measured intensity

lnðc

þ 1Þ

ð17Þ

where T

is called the equivalent blackbody temperature or, more commonly, bright-

ness temperature. It provides a more physically recognizable way to describe

intensity.

4 ABSORPTION AND EMISSION IN GASES: SPECTROSCOPY

The theory of blackbody radiation was developed with solids in mind, and in the

atmospheric sciences is most applicable to solid and liquid materials such as ocean

and land surfaces and cloud particles. The emissivity of surfaces and suspended

particles is generally high in the thermal part of the spectrum, and tends to change

fairly slowly with wavelength.

In gases, however, emissivity and absorptivity change rapidly with wavelength, so

blackbody radiation is not a useful model. Instead, it is helpful to consider how

individual molecules of gas interact with radiation; then generalize this understand-

ing by asking about the behavior of the collection of molecules in a volume of gas.

We will ﬁnd that the wavelengths at which gases absorb and emit efﬁciently are

those that correspond to transitions between various states of the molecule; under-

standing the location and strength of these transitions is the subject of spectroscopy.

Spectral Lines: Wavelengths of Absorption and Emission

Imagine the simplest possible atom, a single elect ron of mass m

circling a single

proton. In a mechanical view the electrostatic attraction between the unlike charges

balances the centripet al acceleration of the electron, so the velocity v of the electron,

and therefore its angular momentum, are related to the distance r between the

310 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

electron and the proton. In 1913 Niels Bohr postu lated that the angular momentum

of the electron is quantized, and can take on only certain values such that

vr ¼

ð18Þ

where n is any positive integer. This implies that the electron can only take on certain

values of v and r, so the total energy (kinetic plus potential) stored in the atom is

quantized as well. If the energy levels of the atom are discrete, the changes between

the levels must also be quantized.

It is these speciﬁc changes in energy levels that determine the absorption and

emission lines, the wavelengths at which the atom absorbs and emits radiation. The

energy of each photon is related to its frequency and so its wavelength

E ¼ hn ¼

ð19Þ

A photon striking an atom may be absorbed if the energy in the photon corre-

sponds to the difference in energy between the current state and another allowed

state. In a population of atoms or molecules (i.e., in a volume of gas) collisions

between molecules mean that there are molecules in many states, so a volume of gas

has many absorption lines.

In the simple Bohr atom the energy of the atom depends only on the state of the

electron. Polyatomic molecules can contain energy in their electronic state, as well as

in their vibrational and rotational state. The energy in each of these modes is

quantized, and photons may be absorbed when their energy matches the difference

between two allowable states in any of the modes.

The largest energy differences (highest frequencies and shortest wavelengths,

with absorption=emission lines in the visible and ultraviolet) are associated with

transitions in the electronic state of the molecules. At the extreme, very energetic

photons can completely strip electrons from a molecule. Photodissociation of ozone,

for example, is the mechanism for stratospheric absorption of ultraviolet radiation.

Energy is also stored in the vibration of atoms bound together in a stable mole-

cule. Vibrational transitions give rise to lines in near-infrared and infrared, between

those associated with electronic and rotational transitions. The amount of energy in

each vibrational mode of a molecule depends on the way the individual atoms are

arranged within the molecule, on the mass of the atoms, on the strength of the bonds

holding them together, and on the way the molecule vibrates. Vibrational motion can

be decomposed into normal modes, patterns of motion that are orthogonal to one

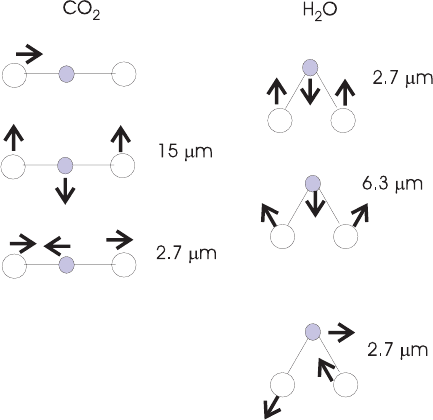
another. In a linear symmetric molecule such as CO

, for example, the patterns are

symmetric stretch, bending, and antisymmetric stretch, as shown in Figure 3. The

state of each normal mode is quantized separately.

The way atoms are arranged within a molecule also plays a role in how energy is

stored in rotational modes. Carbon dioxide, for example, contains three atoms

arranged in a straight line, and thus has only one distinct mode of rotation about

4 ABSORPTION AND EMISSION IN GASES: SPECTROSCOPY 311

the center molecule and one quantum number associated with rotation. Complicated

molecules like ozone or water vapor, though, have three distinct axes of rotation, and

so three modes of rotation and three quantu m numbers associated with the rotational

state, each of which may change independently of the others. For this reason the

absorption spectrum of water is much more complicated than that of CO

Changes in vibrational and rotational states may also occur simultaneously, lead-

ing to a very rich set of absorption lines. Becau se the changes in energy associated

with rotation are so much smaller than those associated with vibration, the absorp-

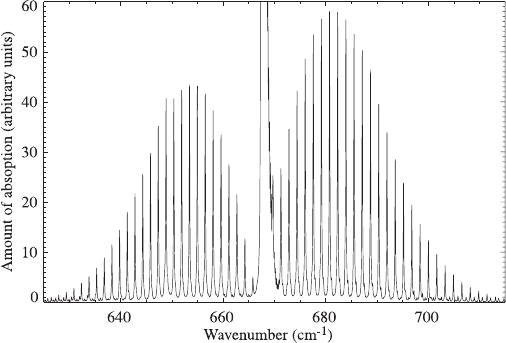
tion spectrum appears as a central line with many lines (each corresponding to a

particular rotat ional change) clustered around it, as shown in Figure 4. More

energetic lines (with higher wavenumbers and shorter wavelengths) are associated

with simultaneous incre ases in the rotational and vibrational state, while the lines to

the left of the central line occur when rotational energy is decreased while vibra-

tional energy increases.

What gives rise to the family of absorption lines ﬂanking the central wavenumber

in Figure 4? Carbon dioxide has only one axis of rotation, so the different energies

are all associated with the same mode, but the family of lines implies that there is a

set of rotational transitions, each with a different energy. If J is the quantum number

describing the rotational states, and DJ the change between two states, there are two

possibilities. The different lines might correspond to different values of DJ, but this

is prohibited by quantum mecha nics. In fact, each line corresponds to DJ ¼1, but

neighboring states differ in energy by various amounts depending on J.

Figure 3 Vibrational normal modes of CO

and H

O molecules. Any pattern of vibration

can be projected on to these three modes, which are all orthogonal to one another. Also shown

are the wavelengths corresponding to each vibrational mode. See ftp site for color image.

312

RADIATION IN THE ATMOSPHERE: FOUNDATIONS

Line Strength

The quantum mechanics of electronic, vibrational, and rotational transitions deter-

mines the location of absorption and emission lines in gases. Molecules do not ﬂoat

freely in the atmosphere, however, but rather are members of a large ensemble, or

population. The temperature of the gas determines the mean energy of the mole-

cules, and random collisions between them redistribute the energy among the possi-

ble states. The amoun t of absorption due to any particular transition, then, is the

product of how likely the transition is (as determined by quantum mechanics) and

the fraction of molecules in the originating state. The effectiveness of absorption is

called the line strength S and has dimensions of area per mass or per molecule.

Line strength depends in part on temperature. The atmosphere is almost every-

where in thermal equilibrium, which means that the average amount of energy per

molecule is determined by the temperature, but this energy is constantly being

redistributed among molecules by frequent collisions. The collisions also transfer

energy between different states, so that a fast-moving molecule may leave a collision

moving more slowly but rotating more rapidly. The abundance of molecules in a

state with energy E depends on the ratio of E to the average kinetic energy kT. This

explains the increase and decrease of line strengths to either side of the central line in

Figure 4: The most common rotational state is J ¼7orJ ¼8, and the number of

molecules in other states, and so the line strength, decreases the more J differs from

the most common value.

Line Shape

Each molecular transition, be it electronic, vibrational, or rotational, corresponds to a

particular change in energy, which implies that absorption and emission take place at

Figure 4 Pure vibration and vibration-rotation lines near the 15 mm (666 cm

1

) absorption

line of carbon dioxide. The spectrum is computed for gases at 300 K and 1000 mb.

4 ABSORPTION AND EMISSION IN GASES: SPECTROSCOPY 313

exactly one frequency. But as Figure 4 shows, absorption and emission occur in a

narrow range of wavelengths surrounding the wavelength associated with the transi-

tion. We say that absorption lines are affected by natural broadening, pressure

(or collision) broaden ing, and Doppler broadening. We describe these effects in

terms of a line shape function f ðn  n

Þ, which describes the relative amount of

absorption at a frequency n near the central transition frequency n

. Line broadening

affects the spectral distribution of absorption but not line strength.

Natural Broadening of Absorption Lines

Natural broadening of absorption lines has a quantum mechanical underpinning.

Because molecules spend a ﬁnite amount of time in each state, the Heisenberg

uncertainty principle tells us that the energy of the state must be somewhat uncertain.

This blurring of energy levels implies a similar blurring in the transition energies

between levels, though the effect is small compa red to other broadening

mechanisms.

Doppler Broadening of Absorption Lines

If we stand beside a racetrack and listen to an approaching car, the whine of the

engine will seem to increase in pitch, then decrease as the car passes us. This change

in frequency is known as the Doppler shift and occurs whenever an object and

observer move relative to one another. The frequency n of the emitted sound or

light appears to increase or decrease from its unperturbed value n

depending on how

fast the object moves v relative to the speed of the wave c:

n ¼ n

1 



ð20Þ

Because the atmosphere is almost always in thermal equilibrium, the velocities of

a collection of gas molecules follow a Maxwell–Boltzmann distribution. The pro-

bability p(v) that a molecule will have a radial velocity v depends on the temperature

T, since molecules move faster at higher temperatures, and on the mass m of the

molecules

pðvÞ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2pkT

exp 

2kT



ð21Þ

We can compute the Doppler line shape f

ðn  n

Þ around an absorption line by

combining (20) and (21):

ðn  n

Þ¼

ﬃﬃﬃ

exp 

ðn  n

ð22Þ

314 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

where we have deﬁned the Doppler line width

ﬃﬃﬃﬃﬃﬃﬃﬃ

2kT

ð23Þ

Absorption lines associated with heavier molecules are broadened less than those

associated with light molecules, since for the same mean thermal energy (as

measured by temperature) heavier molecules move more sluggishly than light

ones. Doppler broadening also increases in importance at shorter wavelengths. It

has the greatest effect high in the atmosphere, where pressure is low.

Pressure Broadening of Absorption Lines

When pressure is high, however, collision or pressure broadening is the most import-

ant process determining the shape of absorption and emission lines. The exact

mechanisms causing pressure broadening are so complicated that there is no exact

theory. What is clear, however, is that the width of the absorption line increases as

the frequency of collisions between molecules increases. Pressure-broadened spec-

tral lines are well-characterized by the Lorentz line proﬁle:

ðn  n

Þ¼

ðn  n

þ a

ð24Þ

The Lorentz line width a

depends on the mean time t between collisions:

2pt

ð25Þ

In practice the value of a

is determined for some standard pressure and temperature

and T

, then scaled to the required pressure and temperature using kinetic theory:

¼ a



ð26Þ

where n varies but is near

. When molecules collide with others of the same

species, we say that the line is self-broadened; when the collisions are primarily

with other gases we say the line is subject to foreign broadening. For the same

width pressure broadening affects the line wings, those frequencies further from

the central frequency, more dramatically than Doppler broadening, as Figure 5

demonstrates.

Both pressure and Doppler broadening can occur simultaneously. The line shape

that results, the convolution of f

ðn  n

Þ and f

ðn  n

Þ, is called the Voigt line

shape, which does not have an exact analytic for m. It is instructive, though, to

4 ABSORPTION AND EMISSION IN GASES: SPECTROSCOPY 315