Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

Growth by Coalescence Two methods have been used for calculating growth

rates of cloud droplets by coalescence. The ﬁrst, called continuous collection, is used

to calculate the growth of single drops that pass through a cloud of smaller droplets.

These single drops are assumed not to interact with drops of similar size so as to lose

their identity. The continuous collection equation is

KðR; rÞw

ðrÞDr ð23Þ

where M is the mass of the drop, K is the collection kernel, and w

is the liquid water

content per unit size inter val Dr. The collection kernel, the volume of air swept out

per unit time by the larger drop, is given by K ¼ pEðR þ rÞ

½V

ðRÞV

ðrÞ, and

¼ nðrÞ4pr

=3, where E is the collection efﬁciency, V

(R) and V

(r) are the

terminal velocities of the large and small drops, r

is the liquid water content, and n

is the small droplet concent ration.

Calculations show that small raindrops can form in about 20 to 30 min provided

coalescence nuclei (R > 50 mm) are present in the c loud and the smaller cloud

droplets have radii of at least 7 mm. Szumowski et al. (1999) applied the continuous

growth equation in marine cumulus using a Lagrangian drop-growth trajectory

model in wind ﬁelds derived from dual-Doppler radar analyses. The evolution of

the radar-observed clouds in this study provided a strong constraint on the growth of

raindrops. Raindrops were found to grow to sizes ranging from 1 to 5 mm from

coalescence nuclei in about 15 to 20 min. Their calculations suggest that coalescence

growth is efﬁcient in marine clouds that contain giant and ultragiant sea salt aerosol

and low (100 to 300 cm

3

) droplet concentrations. In continental clouds, which

generally have narrow droplet distributions and high (800 to 1500 cm

3

) droplet

concentrations, continuous growth may take signiﬁcantly longer.

In nature, the droplets composing a cloud have a continuous distribution of sizes,

and droplets of all sizes have the potential to collide with drops of all other sizes. The

drops of most importance to the precipitation process occupy the large end tail of the

drop size distribution. To consider rain formation, the statistical aspects of interac-

tions between droplets must be considered. There is an element of probability

associated with the collection process, and, occasionally, collisions will occur

between larger droplets. A general method for calculating coalescence growth is

to assess the probability that droplets of one size will collect droplets of another size

for all possible droplet size pairs in the droplet distribution. The term stochastic

collection is applied when the collection probability is used to determine the number

of droplets of a given size, r, that are created by collisions of smaller pairs, r 7Dr

and r 7Dr

, and destroyed by collisions of r with other droplets. Stochastic collec-

tion considers rare collisions between larger droplets and consequently predicts

accelerated coalescence in warm clouds.

Possible interacti ons between drops include small droplets collecting small

droplets (autoconversion), large drops collecting small drops (accretion), and

large drops collecting large drops (large hydrometeor self-collect ion). Bulk

microphysical cloud models often parameterize these three proces ses. Another

286 MICROPHYSICAL PROCESSES IN THE ATMOSPHERE

outcome is droplet breakup where two drops collide with the result being a number

of smaller drops.

Collisions between large drops will result in a dramatic broadening of the tail of

the distribution and an increase in the size and number of precipitating drops.

However, these drops are in such low concentration that collisions of this type

must be considered a rare event from a statistical point of view. Simulations of

the collection process using stochastic approaches must accurately consider the

most rare events.

The continuous form of the stochastic coalescence equation is given by:

@Nðm; tÞ

Nðm

; tÞNðm  m

; tÞKðm

; m  m

Þdm



Nðm; tÞNðm

; tÞKðm; m

Þdm

ð24Þ

where N is the concentration of drops of mass m at time t and K is the collection

kernel. The ﬁrst term describes the coalescence of two drops of mass m

and m 7 m

to form a droplet of mass m. The average concentration of drops of mass m will

increase for every coalescence of two smaller drops of mass es m

and m 7 m

.For

every two drops ‘‘destroyed’’ one is created, thus the factor of

. The second term

describes coalescence of drops of mass m with drops of mass m

. This ter m repre-

sents the ‘‘destruction’’ of drops of mass m, since any mass m drop that combines

with any other drop will no longer be mass m.

Care must be taken to avoid numerical diffusion when integrating the stochastic

collection equation. Considerable efforts have been made to develop integration

schemes that accurately portray the evolution of the droplet spectra. Berry and

Reinhardt’s (1974) study indicated that the formation of raindrops in warm clouds

can be fairly rapid. In their numerical experiments, initial droplet sizes were speci-

ﬁed using gamma distributions of their masses, with the liquid water content as

1g=m

and mean drop sizes ranging from 10 to 18 mm radius (see example in

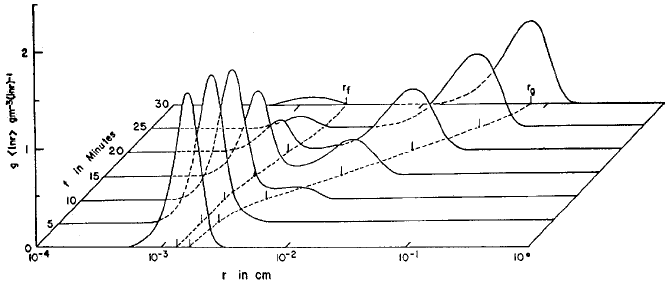
Fig. 18). Drizzle drops were produced in 10 to 22 min and raindrops in 20 to

30 min in different experiments. Faster growth occur red for larger mean initial

sizes. The growth of drops after they reached drizz le drop size was nearly indepen-

dent of the drop spectrum. Berry and Reinhardt’s studies show that growth of rain-

drops in warm clouds can occur by stochastic processes within time scales observed

in nature, provided the initial spectra has sufﬁciently large mean radii and the spectra

contain droplets with radii of at least 30 mm radius.

5 GROWTH OF ICE PARTICLES IN ATMOSPHERE

Ice crystals form in the atmospher e through either homogeneous or heterogeneous

nucleation. Once formed, ice particles grow by three mechanisms: diffusion of water

vapor, accretion of supercooled droplets, and aggregation with neighboring crystals.

5 GROWTH OF ICE PARTICLES IN ATMOSPHERE 287

Accretion leads to the formation of graupel and hail, while aggregation produces

snowﬂakes. Ice particles sometimes shatter during growth or evaporation, increasing

particle concentrations. Mechanisms that enhance ice particle concentrations in

clouds in this manner are called secondary ice particle product ion mechanisms.

Diffusional Growth of Ice Particles

The Clausius–Clapeyron equation describes the equilibrium condition between two

phases. By comparing the solution of the Clausius–Clapeyron equation for the cases

of water and vapor, and ice and vapor, it can be easily shown (e.g., Rogers and Yau,

1989; Pruppacher and Klett, 1997) that the saturation vapor pressure over water,

s, 1

, will always exceed the saturation vapor pressure over ice, e

si, 1

, for T < 0



This is a consequence of the fact that the latent heat of sublimation, L

, is larger than

. This difference has major implications for the growth of ice in clouds. Air

saturated with respect to ice will always be subsaturat ed with respect to water.

Conversely, air saturated with respect to water will always be supersaturated with

respect to ice. As a consequence, superc ooled water droplets and ice crystals can

never exist in a cloud together in equilibrium. Ice crystals, always subject to greater

supersaturations, will rapidly grow, extracting vapor from the surroundings, while

coexisting supercooled droplets will evaporate, supplying vapor to the surroundings.

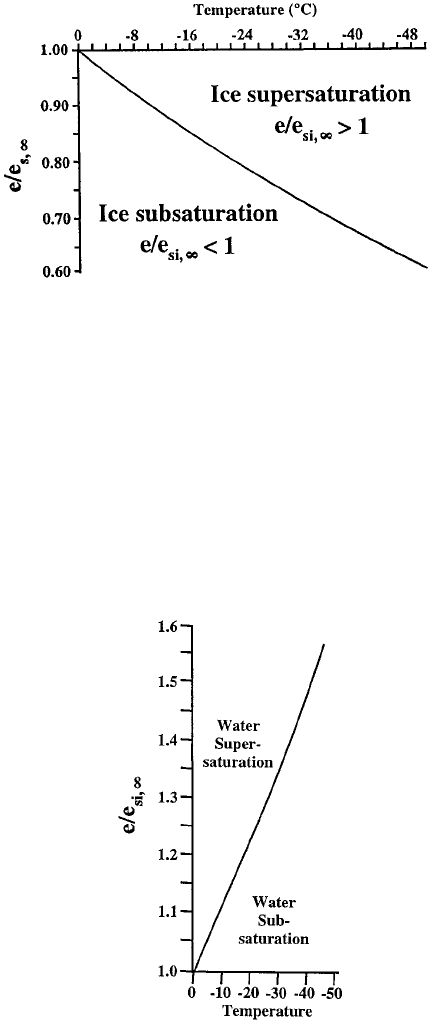
The differences in relative humidity with respect to ice and water as a function of

temperature can be found by taking the ratios e=e

s, 1

and e=e

si, 1

and plotting them

as a function of temperature. Figures 19 and 20 show that, at cold temperatures, air

can be signiﬁcantly below saturation with respect to water (relative humidity wi th

respect to water, RH

65 to 70%) and still be supersaturated with respect to ice.

High in the atmosphere, at cirrus cloud levels, ice crystals can grow at moderate

relative humidities with respect to water. Even at lower altitudes, particularly in

Figure 18 Example of development of a droplet spectrum using stochastic coalescence

(from Berry and Reinhardt, 1974). The radius r

denotes the mean mass, which follows the

cloud droplet peak, and r

denotes the radius of mean-square mass, which follows the raindrop

peak.

288

MICROPHYSICAL PROCESSES IN THE ATMOSPHERE

wintertime, ice particles can grow at RH

< 100%. On the other hand, a cloud that

has a relative humidity with respect to water of 100% will be supersaturated with

respect to ice by a substantial amount. For example, at 10



C, the relative humidity

with respect to ice will be about 112%. At 20



C, it will be 120%. In an environ-

ment where RH

¼100% exactly, water d rops will not grow, yet ice crystals in this

same environment will experience enormous supersatura tions. As a consequence,

they grow very rapidly to become large crystals.

Figure 19 Ice saturation as a function of saturation ratio with respect to water (adapted from

Pruppacher and Klett, 1997).

Figure 20 Water saturation as a function of saturation ratio with respect to ice (adapted from

Pruppacher and Klett, 1997).

5 GROWTH OF ICE PARTICLES IN ATMOSPHERE 289

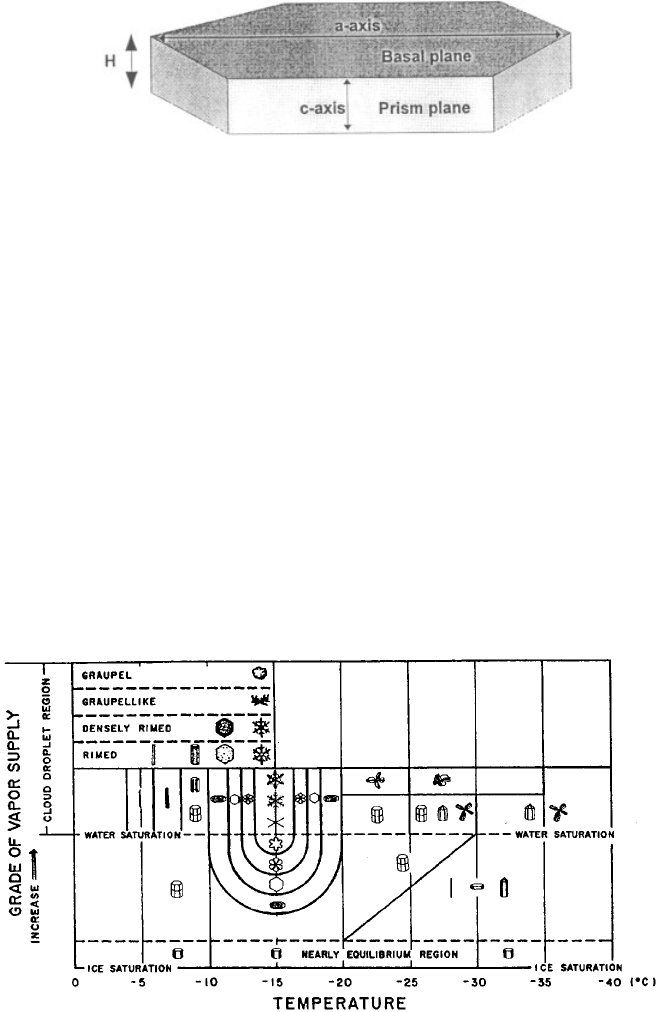
From a crystallographic point of view, ice crystal growth normally occurs on two

planes, the basal and prism planes. The basal plane of an ice crystal refers to the

hexagonal plane illustrated in Figure 21. The axis that passes from the outside edge

of the crystal through the center along the basal plane is called the a axis. The a axis

can be thought of as the diameter of the circle that circumscribes the basal plane. The

prism plane refers to any plane along the vertical axis of the crystal, the c axis. Prism

planes appear rectangular in Figure 21. The height of a crystal, H, is shown in

Figure 21. Growth along the basal plane implies that the c axis wi ll lengthen and

H will become larger. Growth along the prism plane implies that the a axis will

lengthen and the diameter of the crystal will become larger.

Laboratory experiments have shown that the rate of growth along the c axis

relative to growth along the a axis of crystals varies signiﬁcantly as a function of

temperature and supersaturation. These variations occur in a systematic manner,

resulting in the characteristic shapes, or ‘‘habits,’’ of ice crystals, summarized in

Figure 22. As temperature decreases, the preferred g rowth axis changes from the a

axis (platelike crystals, 0 to 4



C) to the c axis (columnar crystals, 4to9



C), to

the a axis (platelike crystals, 9 to about 22



C), to the c axis (columnar crystals,

Figure 21 Geometry of a simple ice crystal.

Figure 22 Natural ice crystal habits that form when crystals grow in different temperature

and humidity conditions (Magono and Lee, 1966).

290

MICROPHYSICAL PROCESSES IN THE ATMOSPHERE

22



C and colder). The ﬁrst two trans itions are well deﬁned, while the latter is

diffuse, occurring between about 18 and 22



C. At high supersaturations with

respect to ice (water supersatur ated conditions), the transition as a function of

temperature is, in the same order as above, a plate, a needle, a sheath, a sector, a

dendrite, a sector, and a sheath. The tem peratures of these transitions are evident

from Figure 22. At low supersaturations with respect to ice (below water saturation),

the transition in habit as a function of temperature is from a plate, to a hollow (or

solid) column, to a thin (or thick) plate to a hollow (or solid) column, depending on

the level of saturation. Observations of ice particles in the atmosphere show that the

same basic habits appear in nature, although the structure of the particles is often

more complicated. This can be understood when one considers that the particles fall

through a wide range of temperatures and conditions of saturation.

Ice particles possess complex shapes and, as a result, are more difﬁcult to model

than spherical droplets. However, the diffusional g rowth of simple ice crystals can be

treated in a similar way as drops by making use of an analogy between the governing

equations and boundary conditions for electrostatic and diffusion problems. The

electrostatic analogy is the result of the similarity between the equations that

describe the electrostatic potential about a conductor and the vapor ﬁeld about a

droplet. Both the electrostatic potential function outside a charged conduct ing body

and the vapor density ﬁeld around a growing or evaporating droplet satisfy Laplace’s

equation. The derivation of the growth equation for ice crystals proceeds exactly as

that for a water droplet, except the radius of a droplet, r, is replaced by the electro-

static capacitance, C, the latent heat is the latent heat o f sublimation, L

, and the

saturation is that over ice, S

i,v

, rather than water. In the case of a spherical ice crystal

C ¼r. The result is

4pCðS

i;v

 1Þ

=KT ðL

TÞ1



þ R

T=De

si;1

ð25Þ

The problem in using this equation is determining the capac itance factor C, which

varies with the shape of the conductor. For a few shapes, C has a simple form. These

shapes are not the same as ice crystals but have been used to approximate some ice

crystal geometries. To use Eq. (25) to determine the axial growth rate of ice parti-

cles, the term dM=dt must be reduced to a form containing each of the axes. In

general, this will depend on the crystal geometr y. To solve for a or c, an additional

relationship is required between da=dt and dc=dt. This relationship is generally

obtained from measurements of the axial relationships determined from measure-

ments of a large number of crystals. Laboratory experiments conducted to determine

the importance of surface kinetic effects in controlling ice crystal growth have shown

that surface kinetic effects are important in controlling crystal habit since kinetic

effects control how vapor molecules are transported across the crystal surface and

incor porated into the crystal lattice. Ryan et al. (1976) has measured the growth rates

of ice crystals in the laboratory. Figure 23 from their study shows that the a axis

5 GROWTH OF ICE PARTICLES IN ATMOSPHERE 291

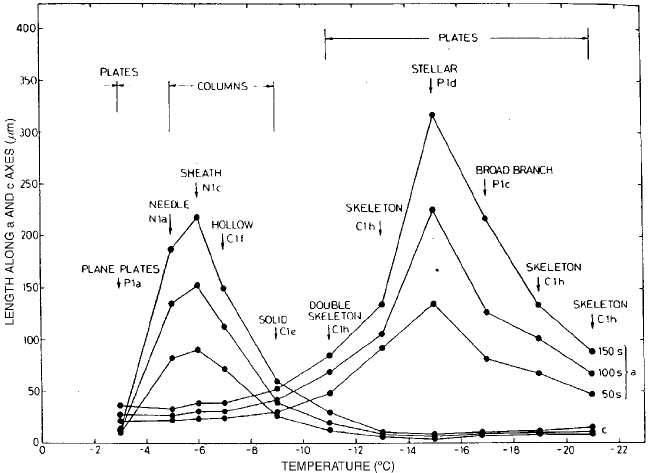
grows most rapid ly at T > 9



C, with a peak at 15



C, while the c axis grows most

rapidly at T < 9



C, with a peak at 6



Ice Particle Growth by Accret ion

Growth by accretion occurs when ice particles collide with supercooled water

droplets, causing them to freeze on to the ice surface. For supercooled water to be

present in substantial quantities in a mixed-phase cloud, it is necessary for the

condensate supply rate to exceed the bulk diffusional growth rate of the ice particles,

after accounting for any dry air entrainment that may be occurring. High condensate

supply rates require sustained large vertical velocities. For this reason, accretion is an

important growth process in clouds with localized regions of sustained high vertical

velocities.

The most common type of cloud that meets this requirement is a cumulus cloud,

particularly cumulus clouds with large vertical development. Regions of other types

of cloud systems also have sustained high vertical velocities. Exa mples include

orographic clouds, par ticularly near the maximum terrain slope, and convective

cores of frontal bands. A second way supercooled water can appear in a cloud is

through vertical transport of droplets upward through the 0



C level. This process can

occur in any type of cloud with a moderate updraft near the melting level. The

supercooled water in this case will generally be conﬁned to the warmer range of

Figure 23 Variation of crystal axial dimensions with temperature for 50, 100, and 150 s after

seeding (Ryan et al., 1976).

292

MICROPHYSICAL PROCESSES IN THE ATMOSPHERE

subfreezing temperatures. Clouds that generally do not contain much supercooled

water are those with weak vertical velocities, such as stratus clouds. In such clouds,

the accretion process will not be as important, if it occurs at all.

Studies of accretion have focuse d primarily on the conditions required for riming

onset, and the late stages of riming, when the particles reach the graupel or ha il stage

of growth. The onset of riming has been studied theoretically and in ﬁeld and

laboratory experiments. These studies generally show that platelike crystals must

grow to a threshold size of about 150 mm radius before any droplets accret e to their

surfaces. Droplets must be larger than about 5 mm radius before they are collected.

Collection efﬁciencies increase with increasing ice particle and cloud droplet size,

reaching about 0.9 when the ice particle radius approaches 400 mm and the droplet

radius reaches 35 mm.

Graupel develops in a cloud when small supercooled cloud droplets collect in

large numbers on falling ice particles. The parent ice pa rticle, or embryo, of a

graupel particle can have various shapes. Certain types of ice particles serve as

graupel embryos more effectively than others. Studies have shown that aggregates

of ice crystals can provide excellent graupel embryos in hailstorms because of their

ability to rapidly collect water droplets. Aggregate embryos can be entrained into the

main updraf t core of hailstorms from the debris clouds of previously active convec-

tive towers. Large drops present in the core updraft can also serve as graupel

embryos upon freezing. Graupel characteristics, including density, mass, and

terminal velocities have been measured in a number of ﬁeld studies. In general,

the data show a great deal of spread, since the observations come from very different

cloud systems.

Hail develops when extreme g rowth by accretion occurs in thundersto rms. Hail

growth occurs in one of two ways, depending on the surface temperature of the

hailstone and the rate of supercooled water accumulation. As a hailston e collects

supercooled water droplets while falling through a thunderstorm, latent heat is

released at the hailstone’s surface as the droplets freeze, raising the surface tempera-

ture, T

, of the hailstone. If T

< 0



C, droplets continue to freeze immediately on the

hailstone’s surface. If, however, T

reaches 0



C, water impacting on the hailstone will

no longer immediately freeze. Water then spreads across the surface of the stone,

drains into porous regions, and can shed from the stone’s surface. The former

situation, when T

< 0



C, is called the dry growth regime. The latter situation,

when T

¼0



C, is called the wet growth regime. For dry growth, the g rowth rate

of the spherical hailstone due to collection of water drops can be approximated by

the continuous collection equation:



dry

¼ EpR

T;H

ð26Þ

where R

is the radius of the hailstone and V

T,H

is its terminal velocity. The terminal

velocity and radius of cloud drops are neglected because they are small relative to R

and V

T,H

[compare Eqs. (23) and (26)]. The same equation applies in the wet growth

5 GROWTH OF ICE PARTICLES IN ATMOSPHERE 293

regime provided the hailstone does not shed water. If the hailstone grows in the wet

growth regime, and sheds excess liquid water from its surface, its growth rate will be

determined by the rate at which the collected water can be frozen. Calculations show

that at 5



C, the effective liquid water content for wet growth is less than 1 g=m

.At

10



C the effective liquid water content is near 1 g=m

. Higher liquid water content

is required for wet growth at colder temperatures. The threshold values of liquid

water content are well within the range of values found in cumulonimbus, implying

that shedding of drops and wet growth are important processes in thunderstorms.

Hailstones exhibit alternating layers of higher and lower density. The density

variations are due to variations in the concentration of bubbles trapped in the

stone. Generally bubbles are grouped in concentric layers of higher and lower density,

which in turn are associated with the different growth regimes. Field studies have

shown that hailstone embryos can be conical graupel, large frozen drops, and occa-

sionally large crystals. Hailstones sometimes exhibit irregular structure while others

have distinct conical or spherical shapes . The largest known hailstone, collected near

Coffeyville, Kansas, weighed 766 g and had a circumference of 44 cm.

Ice Particle Aggregation

Snowﬂakes form through aggregation of ice crystals. Several mechanisms have been

proposed to explain the adhesion of ice particles to one another. Snowﬂakes of sizes

greater than 1 cm are often compo sed of planar and spatial dendritic crystal s, needle-

like crystals or, at higher cloud levels, radiating assemblages of bulletlike crystals.

All of these crystals have shapes that easily interlock during collisions, suggesting

that mechanical interlocking is initially important for crystals to attach to each other.

Two mechanisms have been identiﬁed that bond ice particles together once in

contact. The ﬁrst, called sintering, occurs because ice particles in point contact

form a nonequilibrium system. To minimize the total free surface energy of the

system, a requirement for equilibrium, water molecules must diffuse from ice

surfaces toward the point of contact, strengthening the bond between the particles.

The second bonding mechanism appears to be associated with the presence of a

liquid layer on the surface of ice crystals. This layer is thought to enhance a crystal’s

sticking efﬁciency. Experiments have shown that the surface electrical conductivity

of ice increases signiﬁcantly at temperatures warmer than 10



C, suggesting the

surface contains a quasi-liquid layer. Studies using optical and magnetic resonance

techniques support the existence of the layer. However, the existence of a liquid layer

on the surface of ice crystals at subfreezing temperatures is still not universally

accepted.

Larger aggregates typically ﬁrst develop between 15 and 12



C, the tem pera-

ture range where dendritic crystals form, although aggregates have been observed at

colder temperatures in cirrus. Aggregates form most rapidly near the melting level.

Enhanced aggregation near the melting level is apparently due to increased collec-

tion efﬁciency as a liquid layer develops on the surface of the crystals. The rate of

aggregation in clouds also depends on ice particle concentrations. Calculations and

294 MICROPHYSICAL PROCESSES IN THE ATMOSPHERE

ﬁeld observations both suggest that aggregation is enhanced in the presence of high

crystal concentrations.

Ice Particle Concentrations and Evidence for Ice Multiplication

Ice particles ﬁrst appear in clouds when ice nucleation occurs. Measurements of ice

nuclei suggest that they should be active primarily at cold temperatures (<20



and that the concentration of active nuclei should be an exponential function of

temperature. According to measurements of ice nuclei (Fig. 10), few ice particles

should present in clouds whose tops are warmer than 10



Measurements of ice particle concentrations in clouds have not shown this

expected relationship. Ice particle concentrations often exceed by several orders of

magnitude the concentrations expected on the ba sis of ice nuclei measurements. This

is particularly true at warm temperatures (>10



C). Conversely, at temperatures

between 20



C and the homogeneous nucleation threshold (35 to 40



C) ice

particle concentrations are often less than expected on the basis of ice nuclei

measurements.

Determining the origin of ice particles in clouds remains one of the major

unsolved problems in cloud physics. It is possible that ice nucleation occurs in

clouds under conditions that are not well understood. It is also possible that second-

ary mechanisms for ice enhancement occur. Three mechanisms have been studied

extensively: (1) fragmentation of colliding ice particles, (2) ice splintering during the

riming process, and (3) shattering of drops during freezing.

Ice particles that fragment during collisions are typically more delicate crystals

such as dendrites, sectors, side planes, and needles and sheaths. Particles, that

seldom fragment are thick and thin plates, solid and hollow columns, and scrolls.

Experiments to examine fragmentation show that dendritic crystals readily fragment

in conditions expected in clouds. On the other hand, breakup of rime accumulat ed on

crystals during collisions is unlikely in clouds. Overall, data suggest that only clouds

containing dendritic particles are likely to have a signiﬁcant increase in measured ice

particle concentrations due to fragmentation during collisions.

The high ice particle concentrations observed in clouds provoked a large number

of research groups in the early 1970s to try to ﬁnd a strong ice multiplica tion

mechanism to explain the observations. A breakthrough on the problem was

reported by Hallett and Mossop (1974), who showed that splintering of ice during

the riming process led to copious ice production under a limited range of conditions.

Subsequent studies determined the conditions required for splinter production and

clariﬁed the mechanism for splintering.

These studies together showed that copious numbers of ice splinters could be

produced during riming when: (1) the temperature was between 3 and 8



C; (2)

large ice particles were present in the cloud to co llect cloud droplets, (3) droplets

with diameters >24 mm were present, and (4) droplets smaller than 13 mm diameter

were present. The small droplets, upon freezing onto a falling ice particle, provide

sites for the larger droplets to come into point contact with the ice, attach, and freeze.

Laboratory experiments indicate that supercooled drops accreting on to another

5 GROWTH OF ICE PARTICLES IN ATMOSPHERE 295