Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

Scattering by Small Particles: Rayleigh Theory

When materials are placed within a constant electric ﬁeld, the molecular charges can

become displaced from one another so that the material is polarized. In a traveling

wave the electric ﬁeld varies in time and space; so, in general, different parts of a

particle subject to radiation are polarized differently. But if the particle is very small

compared to the wavelength of radiation (i.e., if x 1), the entire particle is subject

to the same ﬁeld at any given moment. This allows us to treat the radiation scattered

from small particles as if it were emitted from a dipole oscillating at the same

frequency as the incident wave.

The theory of scattering from small particles is named after its developer, Lord

Rayleigh, who published the work in 1871. Rayleigh used an elegant and succinct

dimensional argument to show that the scatt ering efﬁciency varies as the size para-

meter to the fourth power, which for particles of roughly constant size means that

scattering depends strongly on wavelength. The full expression for scattering

efﬁciency is

sca

 1

þ 2



ð53Þ

which implies that scattering cross section depends on the size of the particle to the

sixth power and (if m does not depend too strongly on wavelength) on l

4

. The

theory provides a simple phase function for small particles shown in Figure 9.

Microwave radiation encountering cloud drops is subject to Rayleigh scattering,

which is why radar beams reﬂect so strongly from large drops and preci pitation.

And Rayleigh scattering of visible light by gas molecules is why skies are blue and

sunsets red: Gas molecules are all about the same size, but blue light is scattered

from the incoming sunbeam into the open sky much more efﬁciently than red light.

Scattering by Round Particles: Lorenz–Mie Theory

Some of the most dramatic sights in the atmosphere come from the scattering of

visible light by clouds. Cloud drops are typically about 10 mm in size, and ice

crystals are an order of magnitude larger. For visible light this yields size parameters

much larger than 1, so Rayleigh theory is not applicable. In warm clouds, though,

surface tension acts to minimize the pa rticle surface and make the drops round.

Lorenz–Mie theory, developed around the turn of the twentieth century, takes advan-

tage of this symmetry to develop an exact solution for scattering from homogeneous

spheres. The technique computes the radiation ﬁeld by ﬁnding a series solution to

the wave equation for the scattered wave in spherical coordinates center ed on the

particle, then expanding the incident radia tion in the same coordinates and matching

the boundary conditions.

The application of Lorenz–Mie theory is routine, and codes are freely available

in several computer languages. The calculation requires the relative index of refrac-

tion of the particle and its size parameter and provides the phase function, extinction

326 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

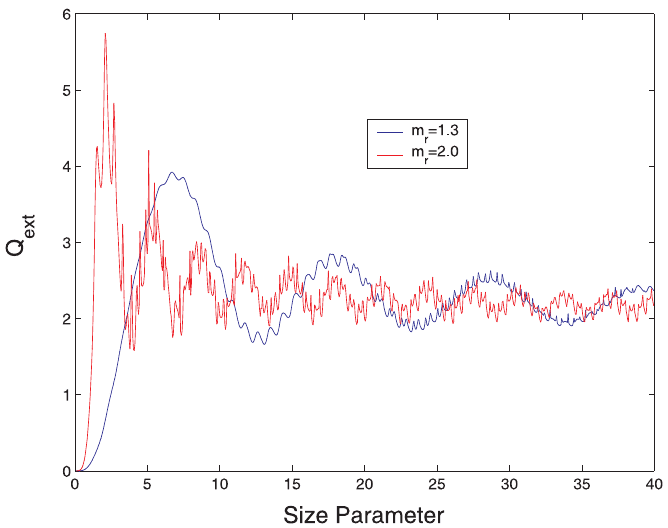
efﬁciency, and single scattering albedo; examples are shown in Figures 8, 9, and 10.

Because the number of terms used to expand the incoming wave increases with

particle size, calculations require more terms as the size parameter increases.

When x is very small, the extinction efﬁciency increases rapidly (echoing

Rayleigh theory) at a rate that depends on the index of refraction. The efﬁciency,

plotted in Figure 8, then oscillates as interference between the scattered and incident

radiation changes from constructive to destructive with small changes in particle

size. At very large values of x (not shown) Q

ext

approaches 2, implying that an area

twice as large as the particle’s cross section is removed from the beam. This is called

the extinction paradox and highlights the role of diffraction in particle scattering. We

might think that a large particle casts a shadow exactly as large as its cross section,

and that this shadow corresponds to the amount of extinction. But every particle has

an edge, and the light passing near this edge is diffracted, or diverted very slightly

from its initial direction. Half of the extinction is due to diffraction and half to

absorption and scattering into other directions. Diffraction contributes to a large

forward peak in scattering phase function of moderately sized, weakly absorbing

spherical particles such as cloud drops in the visible; this peak can be ﬁve or more

orders of magnitude larger than other parts of the phase function, as Figure 9 shows.

Figure 8 Extinction efﬁciency, as computed with Mie theory for spherical particles, as a

function of size parameter and index of refraction. The value asymptotes to 2 (the ‘‘extinction

paradox’’) for large particles as both refraction and diffraction act. See ftp site for color image.

6 SINGLE SCATTERING 327

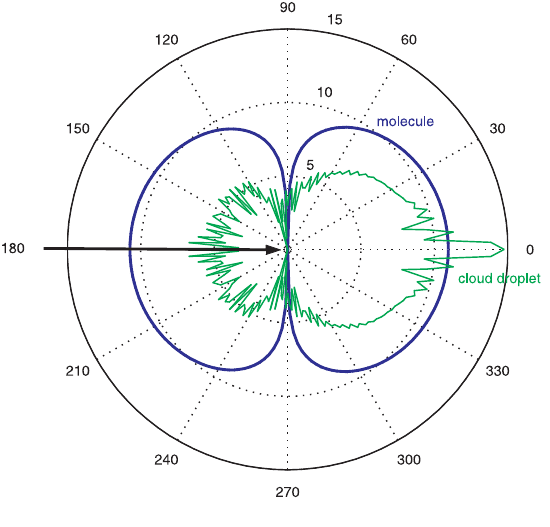
Regardless of drop size or details of the drop size distribution, in fact, the value of

the asymmetry parameter g is always quite near to 0.86 in water clouds.

Scattering by Arbitrary Particles

Mie theory and Rayleigh theory are the two most common methods of computing

scattering from particles in the atmosphere. Neither is appli cable to the scattering of

visible light by either ice crystals or mineral aerosols. Other techniques have been

developed for irregular particles, but these tend to be more complicated and difﬁcult

to use.

Very large particles (size parameters greater than about 50) are said to be in the

‘‘geometric optics limit,’’ and their single scattering properties can be computed by

ray tracing. The particle is oriented in space and a series of inﬁnitely thin rays are

assumed to illuminate it. The direction and intensity is computed using the Fresnel

relations for reﬂection and transmission each time the ray encounters an interface,

and the ray is absorbed as it travels through the medium; the total radiation ﬁeld is

the sum of all the reﬂected and transmitted components for all the rays. Diffraction is

computed separately.

Figure 9 Scattering phase functions for small particles computed using Rayleigh theory

(dark line) and a spherical particle of moderate size parameter. The radial axis is on a

logarithmic scale. See ftp site for color image.

328

RADIATION IN THE ATMOSPHERE: FOUNDATIONS

Irregularly shaped particles of intermediate size are the biggest challenge. If the

phase function is not required, we can use anomalous diffraction theory (ADT) to

ﬁnd the extinction efﬁciency and single scattering albedo. ADT applies to large

particles with an index of refraction near one. It makes the simplifying assumption

that extinction is due primarily to interference between waves slowed by their

passage through the medium, and those diffracted around the particle edge.

Though it ignores inter nal reﬂection and refraction, it is analytically tractable and

reasonably accurate.

Relatively small particles can be treated using the discrete dipole approximation

(DDA), which breaks the par ticle u p in small volumes relative to the wavelength of

radiation, treats each volume as a dipole, and computes the interaction among each

dipole pair. This gets very computationally expensive as the particle size increases,

since the number of dipoles increases as the volume cubed and the number of

interactions as the number of dipol es squared; the current range of applicability is

to size parameters less than 5 to 10.

An alternative to DDA is the ﬁnite-difference time-domain (FDTD) technique.

Here the particle is discretized in space; then electric and magnetic ﬁelds that vary in

time and space are imposed and the solution to Maxwell’s equations is integ rated

forward in time. The incident wave can be monochromatic, but is more commonly a

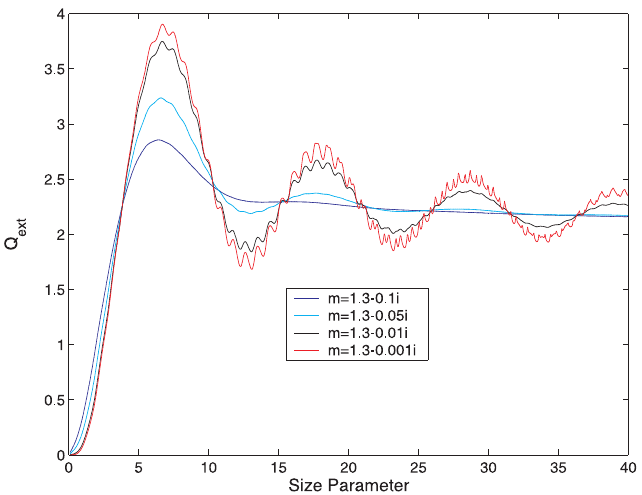
Figure 10 Extinction efﬁciencies of spherical particles for absorbing particles. In more

absorptive materials the variation of Q

ext

with size parameter is damped. See ftp site for color

image.

6 SINGLE SCATTERING 329

pulse, since the latter can provide information about many frequencies at once

through a Fourier analysis. FDTD can be used for size parameters less than 10 to 20.

Integrating over a Particle Size Distribution

Individual photons are scattered by individual par ticles, but in treating a beam of

radiation we have to consider the many different particles encountered along a

differential path dt, so that the phase function, single scattering albedo, and extinc-

tion coefﬁcient represent the entire distribution of drops encountered by the beam.

Because cloud drops and aerosols are separated by distances much greater than their

characteristic size, we can treat each interaction as independent, and simply add up

the contributions from different kinds of particles according to their relative abun-

dance. We have to account for all classes of particles that scatter light uniquely and

must weight the effects according to their contributions to the change in intensity.

Let us make this concrete by asking ourselves how light is scattered within warm

clouds. The drops within a cloud are all round and have the same index of refraction,

but vary in radius r according to the droplet size distribution n(r), which has dimen-

sions of number per volume per radius increment. If we add up all the drops in the

distribution, we ﬁnd the total dropl et number concentration

nðrÞdr ¼ N ð54Þ

where N is measured in number per volume. Drop size distributions within clouds

are often represented with the two-parameter gamma distribution:

nðrÞ¼

GðaÞr



a1

exp 



ð55Þ

in which G(a) is the Euler gamma function, r

a characteristic radius, and a is related

to the variance of the distribution. The gamma distribution is useful because

moments of the drop size distribution can be found analytically.

The scattering properties of the drops depend on the drop radiu s. Each drop has

an extinction cross section C

ext

(r), in units of area; if we add up the contributions

from each drop size, we obtain the volume extinction coefﬁcient k

ext

in units of area

per volume, or inverse length

ext

ðrÞn ðrÞdr ¼

ext

ðrÞnðrÞdr ð56Þ

To compute the average single scattering albedo ho

i we divide the average amount

of scattering by the average amount of extinction:

i¼

sca

ðrÞn ðrÞdr

ext

ðrÞn ðrÞdr

ð57Þ

330 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

while the average phase function is weighted according to the amount of light

scattered by each drop size:

hPðYÞi ¼

PðYÞC

sca

ðrÞnðrÞdr

sca

ðrÞnðrÞdr

ð58Þ

Single scattering parameters are not particularly sensitive to the exact drop size

distribution, but are controlled primarily by the total surface area of drops within

the cloud. The radius associated with the average surface area of the drops is called

the effective radius r

nðrÞdr

ð59Þ

In most water clouds r

is of order 10 mm. The phase function, single scattering

albedo, and extinction coefﬁcient vary smoothly with effective radius, in part

because integration over the size distribution smoothes out rapid oscillations like

those in Figure 8.

The drops within water clouds vary only in their radius, while a collection of

aerosols or ice crystals mig ht contain particles with differing shapes or indices

of refraction. If this is the case the sums (integrals) in (56) though (58) must be

extended to account for every combination of shape, size, and material, but the idea

remains unchanged.

Relating Cloud Optical and Physical Parameters

Imagine a cloud of thickness z made up of drops following a size distribution n(r).

We can compute the optical thickness of this cloud by integrating the extinction

coefﬁcient, given by (56), to ﬁnd

t ¼

ext

dz ¼

ext

ðrÞnðrÞdr dz 

2pr

nðrÞdr dz ð60Þ

where we can make the last approximation in the visible, where cloud drops have

large size parameters.

How can this be related to the cloud physical properties? The liquid water content

(LWC) of this cloud is the sum of the water mass in each drop:

LWC ¼

nðrÞdr ð61Þ

and the liquid water path (LWP) is the liquid water content integrated through the

depth of the cloud:

LWP ¼

LWC dz ¼

nðrÞdr dz ð62Þ

6 SINGLE SCATTERING 331

We multiply (62) by

and use the deﬁnition of effective radius r

from (59):

LWP

2pr

nðrÞdr dz

nðrÞdr

 t

ð63Þ

The last relationship is exact if n( r) is constant with height; the approximation

holds to good accuracy for most distributions and is very useful.

7 SIMPLIFYING THE RADIATIVE TRANSFER EQUATION

The full radiative transfer equati on is usually applied to solar radiation, for which we

know the boundary condition at the top of the atmosphere, namely that the atmos-

phere is illuminated by the sun from a particular direction denoted m

Iðt ¼ 0; m < 0; jÞ¼F

dðm

 mÞ d ðj

 jÞð64Þ

Here F

is the solar ﬂux at the top of the atmosphere and d(x) is the Kroenecker delta

function, with is inﬁnite when its argument is zero and zero otherwise, but integrates

to one.

If sunlight were not scattered, it would obey Beer’s law and intensity would

decrease exponentially with optical depth. This implies that energy traveling in

any direction other than m

, j

has been scattered at least once. We will therefore

decompose the total inte nsity ﬁeld into direct and diffuse components, depending on

whether the photons have or have not been scattered at least once:

Iðt; m; jÞ¼I

dir

ðt; m; jÞþI

dif

ðt; m; jÞð65Þ

The boundary condition in (64) applies to the direct intensity, which is depleted

by any scattering and any absorption, and so follows Beer’s law. There is no incom-

ing diffuse intensity at the top of the atmosphere, but the diffuse intensity can be

increased by scattering from either itself or from the direct beam. The equation

describing diffuse intensity is therefore:

dif

ðm; jÞ

¼I

dif

ðm; jÞð1  o

ÞB 

1

Pðm

; j

! m; jÞI

dif

ðm

; j

Þdm



1

Pðm

; j

! m; jÞ I

dir

ðm

; j

Þdm

¼I

dif

ðm; jÞð1  o

ÞB 

1

Pðm

; j

! m; jÞI

dif

ðm

; j

Þdm



Pðm

; j

! m; jÞ F

exp 



ð66Þ

332 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

The last term in (66) is called the single scattering source term, and the penultimate

contribution is called the multiple scattering source term, which is the redistribution

of diffuse intensity from one direction into another.

In many applications the full details of the intensity ﬁeld are more information

than we need. One of the easiest ways we can simplify the radiative transfer equation

is to average it over azimuth j . We will begin by deﬁning the azimuthally averaged

phase function P

ðm

! mÞ¼

Pðm

; j

! m; jÞdj ð67Þ

and azimuthally average intensity I

ðmÞ¼

Iðm; jÞdj ð68Þ

We then average (66) by integrating both sides over 2p radians in j and dividing the

entire equation by 2p. Since the blackbody source term is isotropic, this results in

¼ I

ð1  o

ÞB 

1

Pðm

; j

! m; jÞIðm

; j

Þdm



Pðm

; j

! m; jÞF

exp 



ð69Þ

We can simplify the second to last term by recalling that the phase function is

reciprocal:

1

Pðm

; j

! m; jÞ I ðm

; j

Þdm

1

ðm

! mÞIðm

; j

Þdm

1

ðm

! mÞI

ðm

Þdm

ð70Þ

which yields the azimuthally averaged radiative transfer equation, from which we

have dropped the subscript:

¼ I ð1  o

ÞB 

1

Pðm

! mÞIðm

Þdm



Pðm

! mÞF

exp

t



ð71Þ

In the remainder of this chapter we will focus on solving (71) rather than any of

the more involved and complete versions of the radiative transfer equation. The

7 SIMPLIFYING THE RADIATIVE TRANSFER EQUATIO N 333

choice is a simpliﬁcation, but it is a very useful one: Most methods for solving the

azimuthally dependent version of the radiative transfer equation use a Fourier expan-

sion in azimuth, and (71) is the lowest order moment in such a treatment.

Delta Scaling

When discussing single scattering, we found that diffraction from particle edges has

as big an impact on extinction as refrac tion within the particle itself, but that this

light is diverted only slightly from its initial direction. Phase functions as strongly

peaked as those in Figure 9 cause numerical headaches in solvi ng the radiative

transfer equation. And in fact, the width of the diffraction peak for cloud particles

is so nar row that the light may as well not be scattered at all.

In most problems in solar radiative transfer we replace the original phase func-

tion, which contains a large, narrow forward peak, with two components: A delta

function in the forward direction and a smoother, scaled phase function. We deﬁne f

as the fraction of light scattered directly forward; then we approximate

Pðcos YÞ2f @ ð1  cos YÞþð1  f ÞP

ðcos YÞð72Þ

We choose the asymmetry parameter of the scaled phase function so that the asym -

metry parameter of the original phase function is unchanged:

g ¼

1

Pðcos YÞd cos Y ¼ f þð1  f Þg

ð73Þ

The value of f can be chosen in a variety of ways, depending on how much infor-

mation is available. One approach is to deﬁne f ¼g so that g

¼0; the more common

delta-Eddington approximation sets f ¼g

We could apply this scaling to any form of the radiative transfer equation that

includes scatteri ng. For the purposes of illustration we will substitute (72) into the

azimuthally averaged radiative transfer equation (71), omitting the source terms for

clarity:

¼ I  f o

I 

ð1  f Þo

1

ðm

! mÞIðm

Þdm

ð74Þ

Dividing both sides of this equation by (1o

f ) yields

ð1  o

f Þdt

¼ I 

1  f

1  o

1

ðm

! mÞIðm

Þdm

ð75Þ

This is exactly the same form as the original equation if we scale variables:

¼ð1  o

f Þto

ð1  f Þo

1  o

g  f

1  f

ð76Þ

so that any technique we have for solving the original radiative transfer equation

works on the scaled version as well. In the scaled system both optical thickness and

334 RADIATION IN THE ATMOSPHERE: FOUNDATIONS

the asymmetry parameter are reduced, so less forward scattering combines with less

extinction to produce the same reﬂection, transmission, and absorption as the

unscaled system. The systems agree, of course, when the direct and diffuse beams

are added together. In practice, almost all calculations of radiative transfer in the

solar system are made using scaled versions of the radiative transfer equation.

8 SOLVING THE RADIATIVE TRANSFER EQUATION SIMPLY

How can we approach the solution of even the azimuthally averaged radiative

transfer equation? Intensity may vary with both optical depth and polar angle m,

and ignoring the vertical variation would mean we could not compute even such

simple quantities as radiative heating rates. We can, however, try to ﬁnd the intensity

at only a few angles. In fact, computing the intensity ﬁeld at just two angles, one

each in the upward and downward hemispheres, is a lot like computing upward and

downward ﬂuxes deﬁned in (5).

Two-stream methods are those that describe the radiation ﬁeld with just two

numbers. They have the advantage of being analytically soluble, which makes

them very fast and thus suitable for, say, use in a numerical climate model. They

are generally good at computing ﬂuxes and therefore useful in heating rate calcul-

ations, but they cannot be used when the angular details of the intensity ﬁeld are

important. There are more than a few two-stream methods, and in every one simpli-

ﬁcations need to be made about both the intensity and the phase function.

The following examples illustrate the computation of ﬂuxes in the visible part of

the spectrum, where there is no emission, but two-stream models are also applicable

to calculations in absorbing and emitting atmosphere.

Eddington’s Solution

In the Eddington approximation we expand both intensity and phase function to ﬁrst

order in polar angle. That is, we assume that each varies linearly with m:

IðmÞ¼I

þ I

m; Pðm ! m

Þ¼1 þ 3gmm

ð77Þ

This means we can compute the upward and downward ﬂuxes analytically:

¼ pðI

 2I

=3Þ F



¼ pðI

þ 2I

=3Þð78Þ

To ﬁnd the intensity we substitute (77) into (71):

dðI

þ I

mÞ

¼ I

þ I

m 

1

ð1 þ 3gmm

ÞðI

þ I

Þdm



ð1  3gmm

ÞF

exp

t



ð79Þ

8 SOLVING THE RADIATIVE TRANSFER EQUATION SIMPLY 335